镉镍蓄电池寿命预测的PF-LSTM建模方法研究

成庶，甘沁洁，赵明，毕福亮，王家捷，王国良，于天剑

镉镍蓄电池寿命预测的PF-LSTM建模方法研究

成庶1，甘沁洁1，赵明2，毕福亮2，王家捷3，王国良3，于天剑1

(1. 中南大学 交通运输工程学院，湖南 长沙 410075；2. 中车长春轨道客车股份有限公司，吉林 长春 130062；3. 青岛亚通达铁路设备有限公司，山东 青岛 266000)

对动车组用蓄电池进行寿命预测，能够评估电池状态，降低故障的危害性和运用维护成本，指导修订修程。相较于在线预测模型，离线预测模型无法适应影响因素的不断变化，提出一种基于粒子滤波(PF)与长短期记忆网络(LSTM)融合的在线预测方法。传统的PF方法依赖经验方程作为状态转移方程，而精确的经验方程难以得到，利用已有数据训练LSTM模型，模型得到的退化方程作为PF的状态转移方程，解决了PF依赖经验方程的问题，同时PF能给出不确定性表达。研究结果表明，该方法模型更新简单有效，预测精度好，弥补了镉镍蓄电池寿命模型研究的缺失，对蓄电池剩余寿命研究的发展有着重要意义。

蓄电池；剩余寿命；在线预测；长短期记忆网络；粒子滤波

不论电力机车还是内燃机车，蓄电池与充电机并联构成了机车控制电路的能量来源，一旦蓄电池出现故障，便无法维持车内照明和无线通信装置以及应急装置的正常使用，对乘客的生命财产安全将带来很大的威胁[1]。通过调研发现，高速铁路车用蓄电池多为碱性镉镍蓄电池，在实际运用中一般根据运行公里数或运用年限进行更换。此时电池寿命往往还有较大余量，提前更换无疑提高了动车组的运用成本。一列机车蓄电池检修费用约为6万元，费时费力且造成了不必要的浪费，研究准确可靠的寿命预测模型刻不容缓。目前在蓄电池剩余寿命预测方面，前人针对锂离子电池、铅酸蓄电池以及燃料电池做了大量研究，但针对镉镍蓄电池寿命预测的模型研究较少，在算法优化及大量数据训练的基础上，本研究提出基于粒子滤波(PF)与长短期记忆网络(LSTM)融合的预测模型，提高了预测精度，为蓄电池剩余寿命研究提供了理论基础。寿命预测方法大致分为2类：模型驱动和数据驱动[2−5]。模型驱动法基于蓄电池的内部结构原理、退化机制建立寿命预测模型，李礼夫等[6]应用电池层析成像测量技术和电化学性能测量技术，根据锂电池内部结构构建了动力电池循环寿命预测模型，但受电池种类、型号等因素影响，该方法难以运用到实际中。Bressel等[7]提出了一种退化模型，使用扩展卡尔曼滤波对燃料电池(PEMFC)在线估计健康度和剩余寿命，该模型对操作条件具有鲁棒性。Jouin等[8−9]将3个粒子滤波器进行组合来预测燃料电池的剩余寿命，新的预测框架能得到95%精度的预测结果。LIU等[10]提出一种新的粒子滤波框架，该框架使用当前测量值来重新采样状态粒子，可以防止粒子的简并，此外还能自适应调整粒子数量，适用于在线应用。实验结果表明，相较于其他标准模型，该模型能以更短时间得到更为精确的预测结果。XIONG等[11]为解决粒子多样性退化的问题，使用突变粒子搜索先验概率的扩展区域，以提高后验概率的精确度。Mejdoubi等[12]将锂电池的老化条件作为预测模型的输入，能够估计电池的容量和电阻，进而得到剩余寿命的预测值，并做了锂电池在不同老化条件下的寿命试验，实验结果表明，相较于标准粒子滤波(PF)，所用模型预测更准确。然而模型驱动法过于依赖故障机理，预测的准确度很大程度上取决于使用的状态模型，而蓄电池工作环境因素复杂多变，建立准确的退化模型较为困难。数据驱动法通过挖掘分析失效数据，得到电池性能退化规律，进而预测电池寿命。Patil等[13]提出了一种基于支持向量机(SVM)实时剩余使用寿命RUL估计方法,分析锂电池不同工况下的循环数据，从电压和温度曲线中提取关键特征，利用这些特征训练模型，从而达到锂离子电池RUL预测的目的。Saha等[14]将等效电路模型参数和老化过程数据结合，用相关向量机(RVM)对PF的预后框架进行改进，进一步提高了预测的精确度，降低了预测的不确定性。同样是RVM与PF的融合方法，周建宝等[15−16]提出一种动态可重构的RVM方法，解决了核函数矩阵和矩阵求逆的计算方法和结构设计等问题，提高锂电池寿命预测的效率。但是相关向量机训练时间较长，导致计算效率和预测精度难以平衡。HU等[17]提供了一种集成数据驱动方法，采用3种加权方案来确定成员算法的权重，并通过k折交叉验证(k-fold cross validation)估计加权方案所需的预测误差。随着神经网络技术的发展，相关方法也应用到了电池寿命预测中来，LIU等[18]使用自适应递归神经网络(ARNN)算法进行动态系统状态预测。ARNN算法采用递归Levenberg-Marquardt(RLM)方法对RNN体系结构的权重进行了几处校正，验证得出自适应RNN具有比经典训练算法(包括RVM和PF方法)更好的学习能力。刘嘉蔚等[19]采用等间隔取样实现数据的重构，采用局部加权回归散点平滑法处理数据，使用核超限学习机对PEMFC寿命试验数据进行学习和预测，实验显示，新方法的准确度比一般神经网络高出28.46%。ZHANG等[20]使用弹性均方反向传播方法自适应地优化长短期记忆网络(LSTM)，实验结果表明，LSTM能得到比支持向量机、标准循环神经网络更准确的预测结果。神经网络对历史数据具有很好的学习能力，但是网络结构难以确定，对数据的样本量和质量要求很高，且不具有输出的不确定性表达。上述研究多针对锂电池和燃料电池，而镉镍蓄电池寿命试验耗时长，试验条件苛刻，目前还未有相关的寿命研究。现有相关研究所用蓄电池的循环寿命为1 000次以下，而某型动车组用镉镍蓄电池寿命周期则高达2 000次以上，电池容量才会降到标准以下。随着周期数的增大，离线方法无法更新模型，误差累加，难有较好的精确度，而在线预测模型能随数据的更新而更新模型，模型的预测精度将更高。此外，镉镍电池具有“记忆效应”的特性，一般的预测方法，难有较好的预测结果。鉴于LSTM有较好的学习能力，PF能很好地适应非线性、非高斯系统，并能给出不确定性表达，因此本文提出融合LSTM与PF2种算法，对蓄电池剩余寿命进行在线预测，该方法能在线更新模型，避免了误差的叠加，LSTM模型训练得到的退化方程作为PF的状态转移方程，解决了PF过度依赖经验方程的缺陷。

1 PF与LSTM的融合方法

1.1 粒子滤波器

粒子滤波器在贝叶斯滤波的基础上，引入蒙特卡洛采样以获得后验概率和随机样本的估计值。假设一个系统其状态方程和观测方程如下：

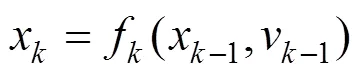
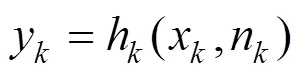
其中：x，y分别时刻的系统状态和观测值；v为过程噪声；n为观测噪声。在蓄电池寿命预测运用中，式(1)通常为经验退化方程，实际工程中精确的退化方程难以获得。为获得目标状态的最优估计，粒子滤波通过预测和更新2个过程来得到系统的后验概率密度(x|Y)。预测阶段利用−1时刻的概率密度(x−1|Y−1)获得先验概率(x|Y−1)：

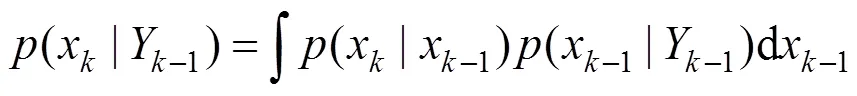
更新阶段利用重要性采样法引入重要性概率密度函数(x|Y)，从中生成采样粒子，利用粒子的加权和来逼近后验概率分布(x|Y)：

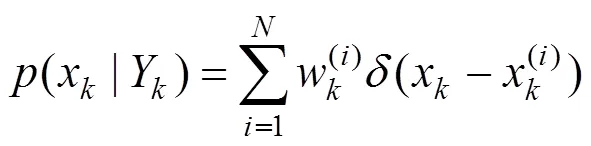
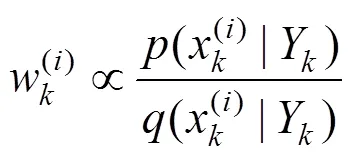
1.2 LSTM

循环神经网络(RNN)可以利用其记忆功能处理非线性时间序列，但是当序列很长时易存在梯度爆炸、梯度消失的问题，长短期记忆网络(LSTM)便是为解决该问题而设计的一种特殊的RNN。相较于RNN，LSTM增加了信息处理单元即细胞cell，该单元由遗忘门、输入门、输出门组成。

遗忘门能以一定概率来丢弃上层的冗余信息：

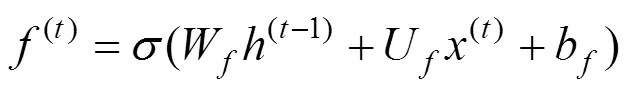
其中：(t−1)为上一层的隐藏状态；(t)为当前序列位置信息；W，U和b为遗忘门中线性关系的权重与偏移量；为sigmoid激活函数。该门将输出一个0到1之间的值，决定信息的丢失程度，0表示“完全舍弃”，1表示“完全保留”。

输入门能处理当前序列位置的信息：

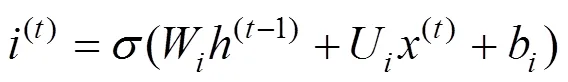
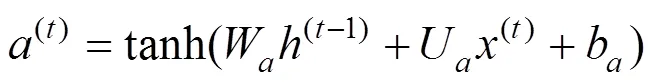
其中：W，U，W和U为输入门中线性关系的权重；b和b为偏移量。遗忘门和输入门的结果将用于细胞状态的更新：

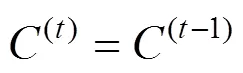
其中：(t)为更新后的细胞状态；⊙为Hadamard积。

输出门则能处理当前序列的信息、细胞状态以及上层隐藏状态，向下一层输出新的隐藏状态：

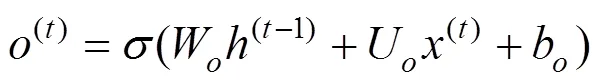
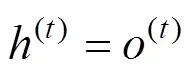
W，U和b为输出门中线性关系的权重与偏移量，(t)为当前层的隐藏状态，既作为当前层的输出，也继续传入下一层。

1.3 融合方法

镉镍蓄电池使用过程中，由于活性物失活，电解液减少等原因，蓄电池的可用容量减小， TB_T3061-2016规定，容量值作为失效判断依据，当容量减少到额定容量的70%时，即为失效。因此通常将电池容量作为性能退化因子，根据退化因子的演变规律来进行寿命的预测。蓄电池寿命受到温度、充放电倍率、工况等多种因素的影响，失效过程是非线性、非高斯的。粒子滤波能很好地适用于非高斯非线性的系统，能够得到预测结果的不准确性表达，但标准的粒子滤波需要式(1)所示的状态转移方程，实际运用中环境等因素变化较大，难以得到较为准确的状态方程。LSTM拥有记忆功能，能够学习长时间跨度的时间序列，但无法适应系统中出现的噪声等不确定因素，且无法给出不确定表达，因此可以融合2种方法，结合各自优点更好地实现蓄电池的寿命预测。

本文选择容量作为退化因子，将前期已有的容量数据建立为时间序列(1,2,3,…,x)，对LSTM模型进行训练学习，基于前个时刻的信息可以得到后一时刻的预测值。

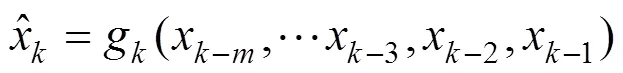
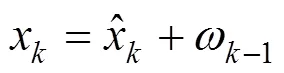
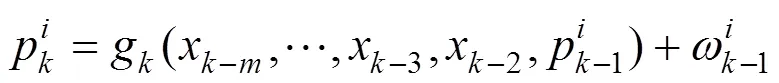
利用重要性采样优化新粒子的权重，越接近状态预测值x的粒子，权重越大，用加权的粒子和逼近第时刻的容量预测值。新增的时间序列用来更新LSTM模型参数。具体流程如图1。

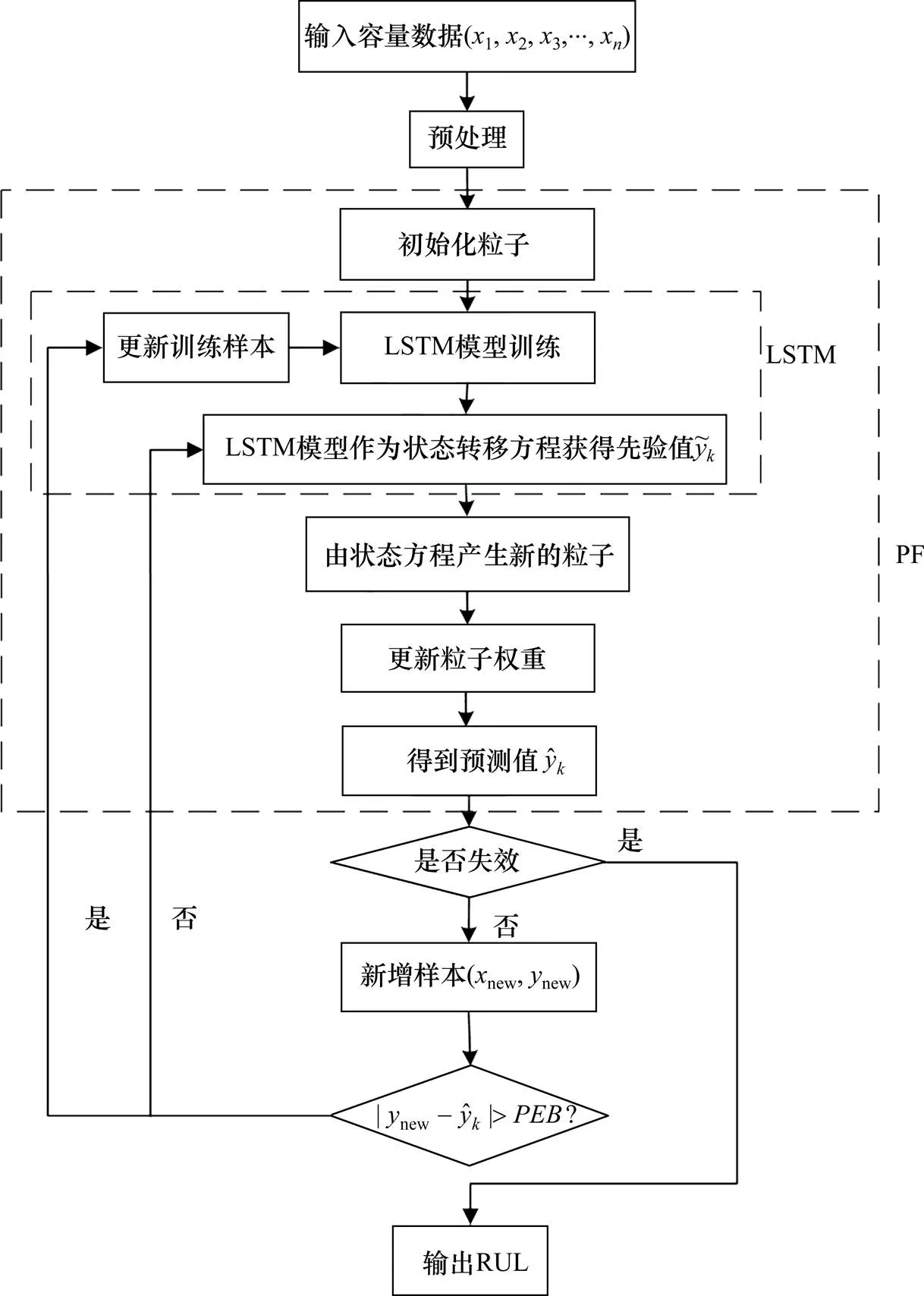
图1 在线预测流程图

Step 1：对容量数据预处理，剔除不可用数据，进行归一化；

Step 3：处理后的数据投入到LSTM中进行学习训练，LSTM中增加dropout模块以防过拟合；

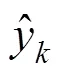
Step 8：当容量到达额定容量的70%，判定为电池失效，预测结束，得到剩余寿命。

2 实验验证

为研究镉镍电池老化特性，使用了多组同类型的动车组车用排气式镉镍电池，单体电池标称电压1.2 V，额定容量160 A∙h，高低温试验箱用于维持试验环境温度，蓄电池组测试系统用于监测电流电压等参数。

图2 实验设备

根据铁标TB_T3061-2016规定在25 ℃±5 ℃环境下进行循环寿命试验，以50次循环为1组，每组循环中的第1次循环以0.25I充电6 h，以0.25I放电2.5 h，2~50次循环以0.2I充电7~8 h，以0.2I放电至1.0 V/节，直至任一50次循环的放电时间少于3.5 h为止，以0.2I再进行1组循环，若连续2组的第50次循环放电时间都少于3.5 h，说明容量下降到额定容量的70%以下，则寿命试验终止。

根据安时积分定理计算得到容量，以容量作为电池性能退化特征：

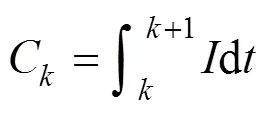
C为第k个充放电周期的容量；为放电电流，得到容量的时间序列，使用归一化函数对数据进行预处理：

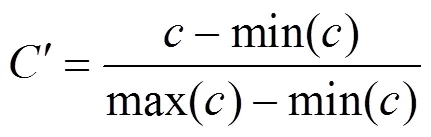
模型的拟合度评价函数：

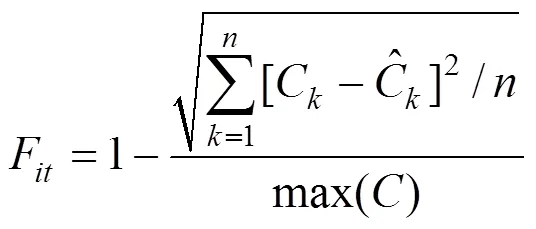
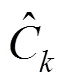
为了验证所提方法的预测效果，使用标准的粒子滤波对实验数据进行预测作为对比。状态转移方程使用指数模型[21−23]：

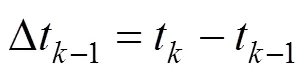
由实验得到，镉镍蓄电池前期因为其特有的“记忆效应”，呈现低容量现象，经过多次彻底的充放电循环后，容量恢复到额定值，在第2 842个周期失效。电池失效的容量门限为112 A∙h，分别以=1 100 cycle，=2 000 cycle为预测起始点，使用预测起点前的实验数据作为训练集，预测起点后数据作为测试集。LSTM模型结构为输入输出层，一个LSTM层，dropout层，以及一个全连接层，优化器使用adam。粒子数目=300，观测噪声协方差=0.000 1。

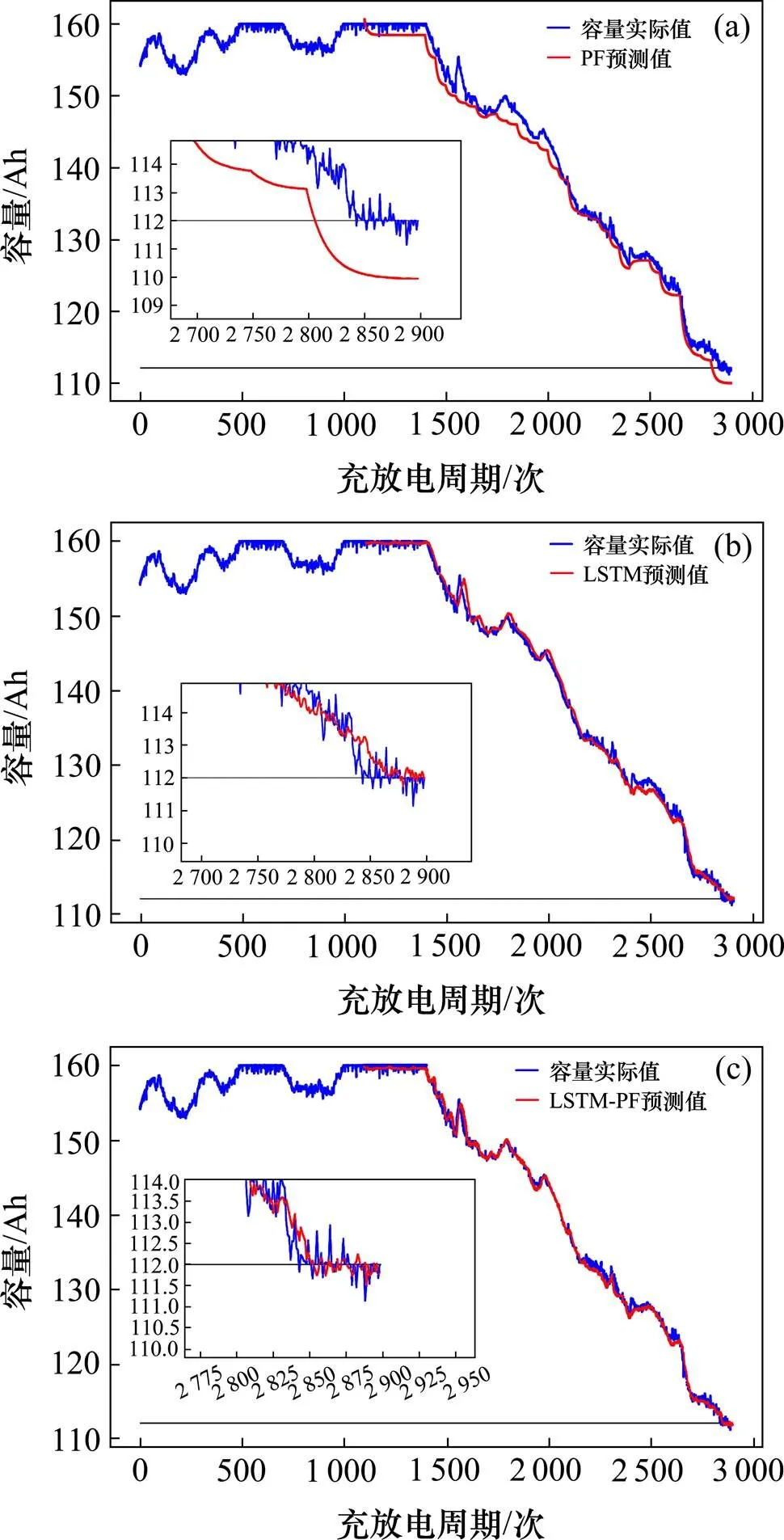
(a) PF模型预测结果；(b) LSTM模型预测结果；(c) LSTM-PF模型预测结果

表1 T=1 100 cycle，实验结果

图3中是预测起始点=1 100 cycle，实际RUL=1 742 cycle，融合模型LSTM-PF，标准PF及LSTM模型的预测对比图，表1为3种模型的结果评价，包括预测结果、误差及拟合度。根据拟合度数据可以看出，融合模型误差更小，且预测误差较PF少27个周期，较LSTM少18个周期。

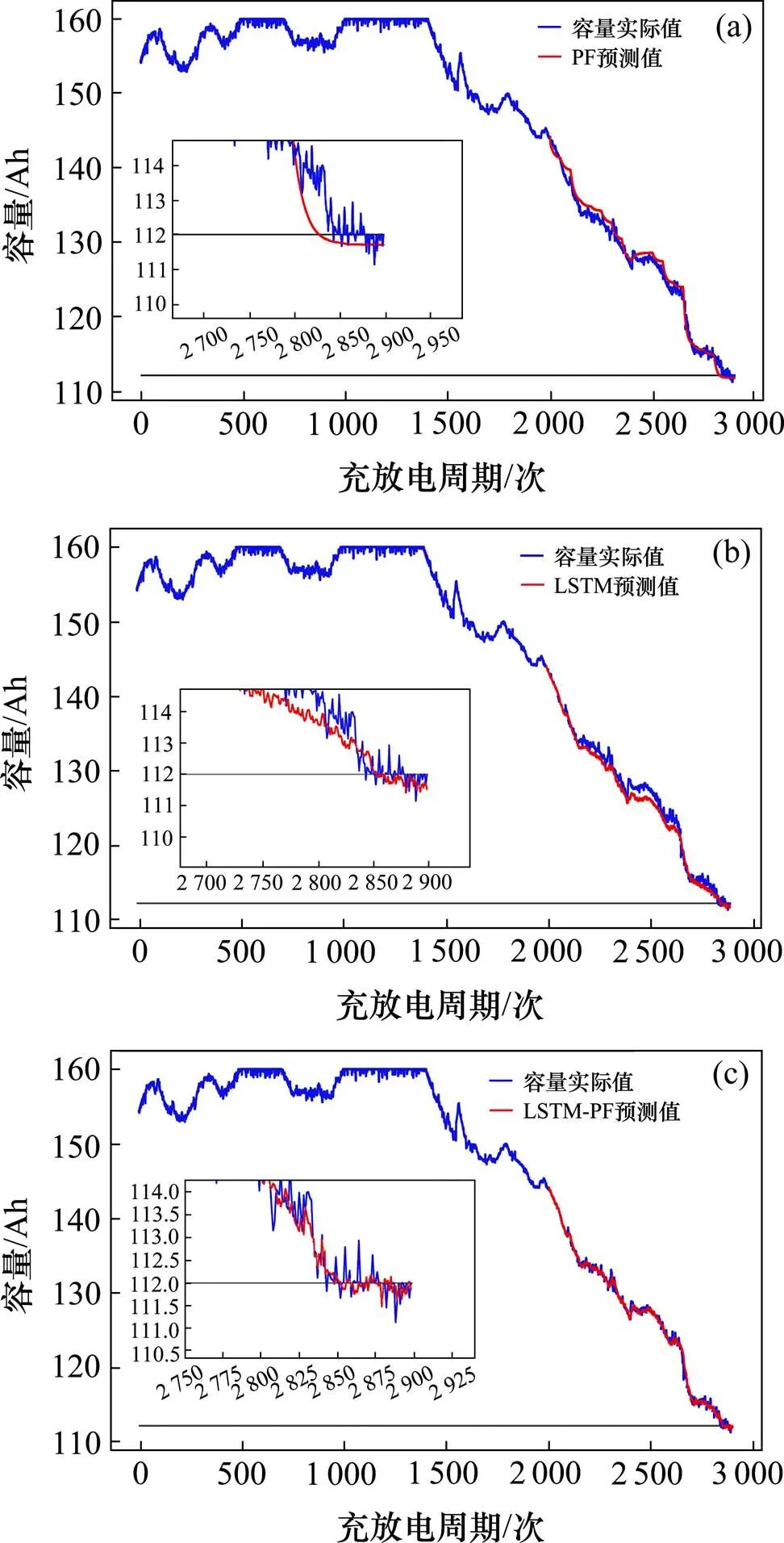
(a) PF模型预测；(b) LSTM模型预测；(c) LSTM-PF模型预测

表2 T=2 000 cycle，RUL预测值

图4中是预测起始点=2 000 cycle，实际RUL=842 cycle，融合模型LSTM-PF，标准PF及LSTM模型的预测对比图，表2展示了3种模型的结果评价，融合模型预测误差较PF少9个周期，较LSTM少5个周期，具有较高的拟合度。

实验结果表明，从同一起始点开始预测时，融合模型比标准的PF和LSTM模型具有更精确的预测结果，而对于3种模型而言，均有当=2 000 cycle时，比=1 100 cycle时预测效果更好，起始点越靠后，意味着更多的数据可以用于训练模型，模型愈加精确。对于同一模型，随着观测数据的更新，预测模型不断学习并更新参数，在线的预测结果也愈加精确。

3 结论

1) 针对高速列车动车组车载镉镍电池进行长时间循环寿命实验，完善了镉镍电池寿命研究的方法，为动车组蓄电池的检修修程提供参考。

2) 融合模型结构简单，LSTM嵌套于PF之中，寿命试验所得容量数据转化为时间序列，用已有历史数据训练LSTM模型得到退化趋势方程，作为PF的状态转移方程，解决PF过于依赖经验模型的问题，PF利用粒子的加权和逼近容量的预测值，能得到剩余寿命的不确定表达，在线方法使得模型参数更新及时，有更好的适应性。

3)从=1 100 cycle，=2 000 cycle 2个起始点进行预测，比较融合模型、标准的PF和LSTM 3种方法的预测结果，结果表明，本文提出的融合方法有着更好的预测精度和拟合度，在后续的研究中将会考虑多变量因素(包括温度、湿度、不同倍率充放电)情况的寿命预测研究。

[1] 张曙光. CRH1型动车组[M]. 北京: 中国铁道出版社, 2008. ZHANG Shuguang.CRH1 electrical multiple units[M]. Beijing: China Railway Press, 2008.

[2] HONG S, ZHOU Z, Zio E, et al. An adaptive method for health trend prediction of rotating bearings[J]. Digital Signal Processing, 2014, 35: 117−123.

[3] TANG S, YU C, WANG X, et al. Remaining useful life prediction of lithium-ion batteries based on the wiener process with measurement error[J]. Energies, 2014, 7(2): 520−547.

[4] XU X, CHEN N. A state-space-based prognostics model for lithium-ion battery degradation[J]. Reliability Engineering & System Safety, 2017, 159: 47−57.

[5] WU J, ZHANG C, CHEN Z. An online method for lithium-ion battery remaining useful life estimation using importance sampling and neural networks[J]. Applied Energy, 2016, 173: 134−140.

[6] 李礼夫, 张东羽. 基于形态与性能的动力电池循环寿命预测方法[J]. 华南理工大学学报(自然科学版), 2018, 46(4): 1−7. LI Lifu, ZHANG Dongyu. An prognostic method power battery remaining useful life based on morphology and performance[J]. Journal of South China University of Technology (Natural Science Edition), 2018, 46(4): 1−7.

[7] Bressel M, Hilairet M, Hissel D, et al. Remaining useful life prediction and uncertainty quantification of proton exchange membrane fuel cell under variable load[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2569−2577.

[8] Jouin M, Gouriveau R, Hissel D, et al. Joint particle filters prognostics for proton exchange membrane fuel cell power prediction at constant current solicitation[J]. IEEE Transactions on Reliability, 2016, 65(1): 336−349.

[9] Jouin M, Gouriveau R, Hissel D, et al. Prognostics of proton exchange membrane fuel cell stack in a particle filtering framework including characterization disturbances and voltage recovery[C]// Prognostics & Health Management. IEEE, 2014:1-6.

[10] LIU Z, SUN G, BU S, et al. Particle learning framework for estimating the remaining useful life of Lithium-ion batteries[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 66(2): 280−293.

[11] XIONG R, ZHANG Y, HE H, et al. A double-scale, particle-filtering, energy state prediction algorithm for Lithium-ion batteries[J]. IEEE Transactions on Industrial Electronics, 2017, 65(2): 1526−1538.

[12] Mejdoubi A E, Chaoui H, Gualous H, et al. Lithium-ion batteries health prognosis considering aging conditions[J]. IEEE Transactions on Power Electronics, 2018, 34(7): 6834−6844.

[13] Patil M A, Tagade P, Hariharan K S, et al. A novel multistage support vector machine based approach for Li ion battery remaining useful life estimation[J]. Applied Energy, 2015, 159: 285−297.

[14] Saha B, Goebel K, Poll S, et al. Prognostics methods for battery health monitoring using a Bayesian framework[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(2): 291−296.

[15] 周建宝, 王少军, 马丽萍, 等. 可重构卫星锂离子电池剩余寿命预测系统研究[J]. 仪器仪表学报, 2013, 34(9): 2034−2044.ZHOU Jianbao, WANG Shaojun, MA Liping, et al.Study on the reconfigurable remaining useful life estimation system for satellite Lithium-ion battery[J]. Chinese Journal of Scientific Instrument, 2013, 34(9): 2034−2044.

[16] 周建宝. 基于RVM的锂离子电池剩余寿命预测方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2013. ZHOU Jianbao. Research on Lithium-ion battery remaining useful life estimation with relevance vector machine[D]. Harbin: Harbin Institute of Technology, 2013.

[17] HU C, Youn B D, WANG P, et al. Ensemble of data-driven prognostic algorithms for robust prediction of remaining useful life[J]. Reliability Engineering & System Safety, 2012, 103: 120−135.

[18] LIU J, Saxena A, Goebel K, et al. An adaptive recurrent neural network for remaining useful life prediction of lithium-ion batteries[C]// Annual Conference of the Prognostics& Health Management Society, 2010: 1−9.

[19] 刘嘉蔚, 李奇, 陈维荣, 等. 基于核超限学习机和局部加权回归散点平滑法的PEMFC剩余使用寿命预测方法[J]. 中国电机工程学报, 2019, 39(24): 7272−7279, 7500. LIU Jiawei, LI Qi, CHEN Weirong, et al. Remaining useful life prediction method of PEMFC based on kernel extreme learning machine and locally weighted scatter plot smoothing[J]. Proceedings of the CSEE, 2019, 39(24): 7272−7279, 7500.

[20] ZHANG Y, XIONG R, HE H, et al. Long short-term memory recurrent neural network for remaining useful life prediction of Lithium-ion batteries[J]. IEEE Transactions on Vehicular Technology, 2018, 67(7): 5695−5705.

[21] 李玥锌. 锂离子电池SOC估计和剩余寿命预测研究[D]. 大连: 大连理工大学, 2017. LI Yuexin. Research on SOC estimation and prediction of RUL of the Lithium-ion battery[D]. Dalian: Dalian University of Technology, 2017.

[22] Saha B, Goebel K, Christophersen J. Comparison of prognostic algorithms for estimating remaining useful life of batteries[J]. Transactions of the Institute of Measurement & Control, 2009, 31(3): 293−308.

[23] Jouin M, Gouriveau R, Hissel D, et al.Combined predictions for prognostics and predictive control of transportation PEMFC[J]. IFAC-Papers on Line, 2016, 49(28): 244−249.

PF-LSTM modeling method for life prediction of Ni-Cd battery

CHENG Shu1, GAN Qinjie1, ZHAO Ming2, BI Fuliang2, WANG Jiajie3, WANG Guoliang3, YU Tianjian1

(1. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China;2. CRRC Changchun Railway Vehicles Co., Ltd, Changchun 130062, China;3. Asiantongdai Railway Equipment Co., Ltd, Qingdao 266000, China)

The life prediction of a battery for an EMU can evaluate the battery status, avoid the occurrence of failures, reduce the cost of investment, and guide the inspection and repair process. Compared with the online prediction model, the offline prediction model can not adapt to the changing conditions and other factors. This paper proposed an online estimation method based on particle filter (PF) and long short-term memory network (LSTM). The traditional PF method relies on the empirical equation as the state transition equation, but the exact empirical equation is difficult to obtain. This paper used the existing data to train the LSTM model, the degenerate equation obtained by the model was used as the state transition equation of PF. The advantages of the approach can solve the problem of PF dependent empirical equations. The PF can give the uncertainty expression. The results show that the method model is simple and effective, and the prediction accuracy is good, which makes up for the lack of research on the remaining useful life model of cadmium-nickel battery. It has important significance for the development of battery residual life research.

nickel-cadmium battery; remaining useful life;online estimation; long short-term memory; particle filter

10.19713/j.cnki.43−1423/u.T20190960

TM912

A

1672 − 7029(2020)07 − 1825 − 08

2020−10−30

国家十三五重点研发计划项目(2017YFB1200902-11)

于天剑(1988−)，男，吉林长春人，讲师，博士，从事电力牵引及传动控制研究；E−mail：250486154@qq.com

(编辑 阳丽霞)