轴向冲击下薄壁方管屈曲模式及初始峰值力控制研究

伊召锋，于尧，高广军，刘东亮

轴向冲击下薄壁方管屈曲模式及初始峰值力控制研究

伊召锋1，于尧2，高广军2，刘东亮1

(1. 中车唐山机车车辆有限公司 技术研究中心，河北 唐山 063035；2. 中南大学 交通运输工程学院 轨道交通安全教育部重点实验室，湖南 长沙 410075)

基于冲击试验和仿真实验手段对带隔板方管吸能结构的碰撞力学响应特性进行分析，建立有限元模型，采用显式动力有限元ANSYS/LS-DYNA进行数值仿真，并与试验结果对比，误差基本稳定在5%以内，验证该数值仿真模型的有效性。研究结果表明：结构变形模式为稳定可靠的轴对称模式。研究隔板结构与诱导结构对吸能特性的影响，得出结构在隔板的约束下产生更多的屈曲褶皱，吸能量提高17%。诱导结构对结构整体吸能量影响不大，可以显著降低结构的初始撞击力峰值，降低百分比达到42.3%。

碰撞；吸能结构；薄壁结构；诱导结构；隔板

列车碰撞事故造成的人员伤亡和财产损失触目惊心[1]。例如，2008年4月28日，2列高速动车组在交济线相撞，造成70人死亡，416人受伤。为了避免或减少碰撞事故造成的损失，提高车辆的耐撞性能是降低碰撞事故影响的最有效方法。许多国家正在进行铁路设备耐撞性研究，旨在开发一种高效的吸能结构作为被动安全防护的主要手段。为了保证碰撞时的安全，需要让列车自身以可控的方式吸收动能，尽可能减小作用于车身的加速度。目前，世界各国对于轨道列车耐撞性设计通常为两端非载人区设计为弱刚度区域，中间车体载人区为强刚度[2]。列车在碰撞过程中，车体端部弱刚度的非载人区率先发生塑性变形，吸收冲击动能，而中间载人区基本不发生变形或者只产生轻微的弹性变形，该设计方案已被公认为目前最有效的耐撞性设计方法[3]。吸能装置安装在车辆的前端，碰撞发生时通过吸能装置耗散能量提高车辆的耐撞性。列车端部吸能结构开发设计成为提高列车耐撞性能的关键，因此对轨道车辆用吸能装置进行研究，对于改善轨道车辆的安全性能具有重要的意义。吸能结构多种多样，每种吸能结构都具有其独特的吸能方式，而被广泛应用于各个耐撞性领域。薄壁金属压溃管作为一种高效吸能结构，在轴向载荷下会发生渐进性屈曲变形模式，从而吸收冲击从动能，在过去几十年间，该结构因其具有质量轻、易加工、成本低、吸能效率高而被广大学者广泛研究。Alexander[4]首先对金属薄壁圆管在轴向载荷下的渐进性屈曲模式进行了理论分析，通过理论模型对圆管吸能量以及吸能模式进行预测。Wierzbichi等[5]基于以上理论模型，开发了超级单元法理论，并结合实验手段，研究了圆管结构在轴向压缩下的屈曲变形模式，发现不同几何参数的圆管会产生诸如手风琴、钻石等不同变形模式，此外不同变形模式吸能能力各不相同。基于超级单元法理论以及试验数段，诸如五边形[6]，六边形[7]，八角形[8]，多胞形[9]和泡沫填充[10]等形式的薄壁结构也被广泛研究。通过比较以上薄壁管结构吸能性能可以得出一个共同点，在非理想冲击载荷下，由于结构抗失稳能力较差，往往造成结构失稳、屈曲褶皱不均匀从而大大降低吸能效率。在轨道列车耐撞性领域，吸能结构所需吸能量巨大，因此吸能结构通常具有较长的纵向尺寸，这对吸能结构能否有效平稳塑变吸能具有极大的挑战[11−12]。李健等[13]为了解决薄壁管存在的缺陷，通过在方管中设置一定数量的隔板，以提高管材的横向强度，从而改善吸能结构的吸能性能。本文在以上基础上设计了一种带隔板约束的方截面锥形薄壁管吸能结构。从而，控制结构的变形模式，达到更好的吸能性能。本文研究带隔板薄壁方形截面管在理想和不完善条件下的轴向屈曲模式。第1部分提出了带隔板方管的几何模型和仿真模型。采用不同的模型对动态过程进行数值模拟。第2部分对吸能结构进行了动态冲击试验研究，第3部分对吸能结构进行了数值仿真研究。并通过试验数据验证了仿真模型的有效性。进而通过数值模拟，研究了吸能结构力学响应特性。第4部分研究了隔板与诱导结构对装置的动力特性影响。

1 结构几何模型

本文设计的薄壁管吸能结构可安装在列车端部弱刚度底架区域，安装位置如图1(a)所示，在列车正常运行过程中，该区域其承载作用，当发生碰撞时，底架吸能结构发生塑性变形，吸收冲击动能。吸能结构由薄壁方管、隔板、端板3部分组成。其中方管由2块对称的U型板结构拼焊而成，管角倒角半径为15 mm，板材厚度为3 mm，方管长度为650 mm，前端端面截面尺寸为147 mm*191 mm，后端端面截面尺寸为147 mm*212 mm。方管4面均开有长条孔，方便与隔板焊接，隔板厚度为3 mm，边长尺寸为对应方管截面区域边长的一半。方管两端分别焊接有2块厚度为20 mm的端板。在结构撞击初期，由于惯性效应的存在，往往产生极大的初始撞击力峰值，对车体结构极为不利，为避免变形开始时出现太大的初始峰值力，本文在结构撞击端设置诱导结构，从而降低装置的初始强度，进而降低初始撞击力峰值，诱导槽宽度为40 mm，长度为110 mm，如图1(b)所示。

2 结构冲击实验

为了验证所设计的高速列车单个吸能组件结构变形稳定性和动作协调性，对单个吸能组件结构进行台车冲击试验。冲击试验采用中南大学碰撞试验台进行，撞击工况为配重台车在空气炮驱动下以一定的速度撞击静止刚性墙，其中刚性墙安装有测力传感器，如图2(a)所示。试验台车可适度调整配重以满足不用试验件的冲击能量。通过单个吸能结构冲击试验，获取结构组件的碰撞动态响应数据(撞击过程中力−时间历程曲线)，验证吸能结构的碰撞耐撞性是否满足设计要求。单个吸能结构组件通过端板焊接固定于试验台车前端，在吸能结构重要部位及试验台车不同位置采用各种标记点进行标记，便于撞击过程中高速摄影仪的动态捕捉和运动序列图像后处理，如图2(b)和2(c)所示。具体试验工况如下：台车与吸能结构总质量为26 674.8 kg，同时以2.94 m/s的速度撞击刚性墙。

根据高速试验仪记录的吸能结构碰撞序列图像，采用运动序列运动图像分析软件，得到吸能结构变形序列，如图3所示。

图3 冲击工况下变形序列

在冲击载荷作用下，压溃行程510 mm，带隔板方管吸能结构产生稳定的变形模式，在撞击瞬间，屈曲褶皱率先在撞击端诱导槽附近产生，并以远离撞击端方向依次发生渐进屈曲，直至撞击结束，整个变形模式与设计变形一致。结构整体并未发生失稳，屈曲变形较为规整。

试验后通过叠加测力传感器得到撞击合力，如图4所示。从撞击力−时间曲线图可以看出，吸能结构撞击刚性墙开始后出现一个峰值力200 kN。随后结构进入稳定屈曲变形过程，撞击力趋向规律化，随着褶皱的产生，撞击力230 kN左右依次形成波峰、波谷状的起伏变化。随着冲击过程的进行，撞击力继续保持502 kN的峰值力后，台车冲击动能基本耗散完毕，撞击力逐渐下降至0，撞击结束。整个撞击过程，吸能结构共耗散了115.3 kJ动能，吸能结构平台力约为226 kN。相对于薄壁方管吸能结构，截面边长与厚度之间的长厚比不同，其对应的变形模式各不相同。当长厚比大于40.38时[14]，结构通常体现的是轴对称变形模式，反之则会出现外延模式或者混合模式，一般而言，方管轴对称变形模式具有更好的稳定性，本文吸能结构厚度为3 mm，长厚比远大于40.38，因此理论上变形模式为轴对称模式，与试验一致。

图4 吸能结构撞击力-位移曲线

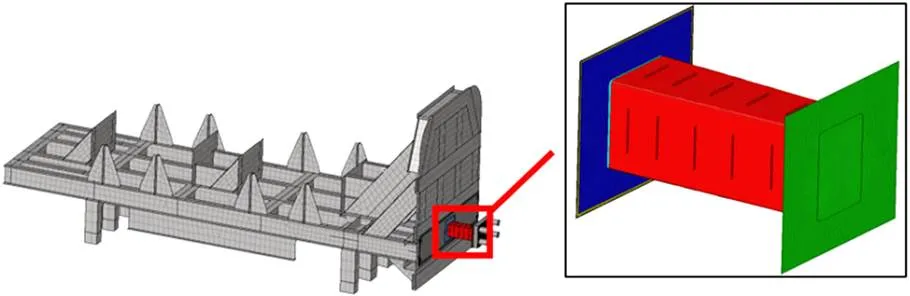
图5 吸能装置有限元模型

3 有限元模型

采用显式动力有限元ANSYS/LS-DYNA对本文建立的吸能结构进行数值仿真，仿真模型的有效性很大程度上影响分析结果的精度，因此建立具有较高可信度有限元模型是整个分析工作的基础。

为节约计算时间，本文对台车车体进行了简化，省略了轮轨结构，通过约束车体自由度，模拟台车纵向运动。吸能结构是板材结构，其横向和纵向长度远远大于其厚度，因此对吸能结构采用壳单元离散，网格单元尺寸为6 mm×6 m，厚度为5 mm。采用面面焊点接触(Contact tied surface to surface)，对吸能结构与台车焊点连接进行模拟分析。模型全局设置自动单面接触(Contact tied surface to surface)算法进行模拟分析，静、动摩擦因数分别为0.3和0.2。吸能结构采用A588高强板材料，采用Cowper- Symonds本构模型[15]，该模型采用与应变率效应相关的因素表示屈服应力：

图7为带隔板方管冲击载荷下塑性变形模式。可以看出，仿真模型变形模式与冲击试验结构的变形模式基本一致，均产生了轴对称式渐进性屈曲模式。屈曲首先从受冲击端的诱导结构开始产生，在隔板的约束下，屈曲褶皱始终产生在隔板之间，并一直延伸到受约束端。仿真与试验均产生了5个完整的屈曲褶皱。图8是冲击试验和有限元仿真的撞击力−位移曲线，可以看出，仿真试验与冲击试验结果基本一致，仿真与试验撞击力曲线均产生了6组完整的波峰波谷序列，其中前5组分别对应5个完整的屈曲褶皱，最后一组是由于方管结构进入密实状态，导致撞击力急剧上升，而此时台车动能刚好耗散完毕，撞击力瞬间下降，从而力值产生较大的波动。

(a) 试验工况；(b) 应力应变曲线

图7 带隔板方管塑性变形模式

图8 冲击和仿真结果对比

冲击试验吸能结构压溃距离为510 mm，吸能量为115.3 kJ，平均撞击力为226 kN，对应的有限元仿真结构压溃距离为518 mm，吸能量为114.8 kJ，平均撞击力为221.6 kN。综合比较后，整个撞击过程中试验与仿真结果二者误差稳定在2%左右，在工程领域[17]，该误差完全在合理范围内，可以认定本文建立的有限元模型具有较高的精度，可将验证过的有限元建模过程进行推广，用于后续结构的耐撞性分析。由于吸能结构在实际加工过程中材料缺陷、以及加工硬化、残余应力等不可避免因素存在，而有限元模型材料本构模型默认材料为理想的各向同性材料，因此并未考虑以上参数，因此导致试验与仿真存在误差。

4 隔板和诱导结构对吸能特性的影响

本节在第3节方管薄壁结构基础上分别取消了隔板结构和诱导结构，并建立了对应的有限元模型，目的是分析诱导结构以及隔板结构对耐撞性的影响。

4.1 隔板结构

薄壁方管能量的耗散主要是冲击载荷作用下壁面塑性铰的弯曲变形，而在形成塑性铰的过程中壁面会产生刚性移动，造成这一部分管壁材料并不吸收能量，因此增加壁面褶皱和壁面变形区域可以有效提升方管的吸能性能。图9为吸能结构最终变形内部剖面图，可以发现，隔板结构在整个冲击过程仅产生了局部轻微的塑性弯曲，并未发生明显塑性大变形。图10为方管薄壁结构与隔板结构吸能量−时间曲线，可以发现，整个吸能过程中，主要以方管结构塑性吸能为主，方管共吸收了110.3 kJ能量，隔板吸收了3.69 kJ能量，仅占总能量的3%，隔板吸能量远小于方管结构，充分验证了整个变形过程中，隔板变形量很小。

图9 结构最终变形剖面图

图10 方管薄壁结构与隔板结构吸能量−时间曲线

图11为取消隔板结构后，吸能结构的变形模式，可以发现没有隔板约束后，吸能结构变形模式仍然为轴对称模式，但是单个屈曲褶皱长度增大，整个撞击过程结构仅产生了3个屈曲褶皱。图12为不带隔板结构的撞击力−时间曲线，可以发现，结构在200 ms之后，产生了一个急剧增加的峰值曲线，最大峰值力达到了1 050 kN，这是由于吸能结构进入密实状态后，由于台车动能仍未耗散完毕，导致结构又产生了一段塑性压缩变形，而该部分吸能量不属于结构的有效塑性内能。表1为分别选取2种结构在450 mm的有效变形行程内的吸能量、平均撞击力以及峰值力撞击结果对比。

表1 带隔板和无隔板仿真结果对比

带隔板结构吸能量为114.8 kJ，不带隔板吸能结构吸能量为84.3 kJ。增加隔板结构，吸能量增加了36%。对应的平均撞击力，带隔板结构也显著高于无隔板结构，撞击初始峰值力带隔板结构显著低于无隔板方管结果。尽管隔板结构并不参与吸能，但是起到了良好的约束变形作用，屈曲褶皱均产生在相邻隔板之间，增加了褶皱数量，从而产生单个褶皱的长度减小，有效增加材料塑性变形利用率，实现了在有限材料内尽可能增加结构的吸能能力。

图11 无隔板结构变形模式

图12 无隔板结构撞击力-时间曲线

4.2 诱导结构

由于结构是焊接结构，在加工过程中会出现误差，以及结构在撞击过程中不存在完全理想碰撞，往往存在一定的撞击偏差，往往导致结构在理想情况和实际试验情况下变形会有较大的差别，因此在设计之初就可以施加人为的变形触发结构，诱导结构产生理想的变形模式，本节着重研究了考虑结构在施加诱导结构下的变形特性。

从图7和图11均可以看出，吸能结构均从诱导槽处率先产生变形，其中有诱导槽两端面首先向内凹陷变形，导致另外两端面向外延展变形，然后各级顺次发生变形，屈曲褶皱呈现出相同的变形规律，整个变形过程稳定可控，结构整体形成标准的轴对称变形模式。图13为结构未施加诱导结构的变形模式，通过观察可以发现，在碰撞初期与3.1和4.1结构不同的是，该结构率先在约束端产生了塑性变形，随后变形沿约束端逐级向撞击端演化，整个变形顺序发生絮乱，导致变形模式杂乱，属于混合变形模式，整个变形模式不是很理想。

初始撞击力峰值是结构防撞性设计中的重要参数，过大的初始峰值力造成碰撞减速度过大，导致结构失稳以及乘员生命安全，因此应尽可能地降低初始撞击力峰值。图14为撞击力曲线，可以发现，在撞击初期出现了明显的峰值力，力值达到了780 kN，带诱导结构模型初始峰值力为450 kN，峰值力降低了42.3%。这说明诱导结构不仅具有诱导结构稳定变形的作用，还具有显著降低撞击力峰值作用。图15为带诱导结构与无诱导结构吸能量曲线，表2为分别选取带诱导结构与无诱导结构方管在450 mm的有效变形行程内的吸能量、平均撞击力以及峰值力撞击结果对比。可以发现，2种结构吸能量数值基本一致，诱导结构对吸能量的影响基本可以忽略。但是由于吸能结构为焊接件，混乱的变形将导致方管壁板产生较大的塑变转角，可能会导致焊缝撕裂，导致不可预期的变形形式。

图14 无诱导结构撞击力曲线

图15 有无诱导结构吸能量对比曲线

表2 带隔板和无隔板仿真结果对比

5 结论

1) 通过吸能结构冲击试验的变形模式表明吸能装置的破坏变形过程稳定有序，变形模式为稳定可靠的轴对称模式，撞击力−位移曲线表明撞击力变化十分平稳，结构的冲击和振动较小，吸能过程比较平稳，可为该吸能装置的设计提供参考依据。

2) 建立有限元模型，采用显式动力有限元ANSYS/LS-DYNA进行数值仿真，数值仿真得到的结构变形模式、撞击力−位移曲线与实验结果相吻合，整个撞击过程中，二者误差基本稳定在5%以内，验证了该数值仿真模型的有效性，可将验证过的有限元建模过程进行推广，用于后续结构的耐撞性分析。

3) 隔板结构在整个冲击过程仅产生了局部轻微的塑性弯曲，基本不参与吸能，但是起到了良好的约束变形作用，屈曲褶皱均产生在相邻隔板之间，增加了褶皱数量，从而产生单个褶皱的长度减小，有效增加了材料塑性变形利用率，实现了在有限材料内尽可能增加结构的吸能能力。

4) 诱导结构对结构整体吸能量影响不大，但是可以显著降低结构的初始撞击力峰值，同时诱导结构产生更稳定可靠的变形模式，在结构稳定性方面具有明显的作用。

[1] Hosseini Tehrani P, Nankali A. Study on characteristics of a crashworthy high speed train nose[J]. Int J Crashworthiness, 2010, 15(2): 161−173.

[2] 高广军, 田红旗, 姚松. 耐冲击吸能车体[J]. 交通运输工程学报, 2003, 3(3): 50−53. GAO Guangjun, TIAN Hongqi, YAO Song. Crashworthy raiway car-body with energy absorbing[J]. Journal of Traffic and Transportation Enginerring, 2003, 3(3): 50− 53.

[3] LI S H, CAI B G, LIU J, et al. Collision risk analysis based train collision early warning strategy[J]. Accident Analysis & Prevention, 2018, 112(3): 94−104.

[4] Alexander J M. An approximate analysis of the collapse of thin cylindrical shells under axial loading[J]. Quarterly Journal of Mechanics and Applied Mathematics, 1960, 13(1): 10−15.

[5] Wierzbichi T, Abramowicz W. On the crushing mechanics of thin-walled structures[J]. Journal of Applied Mechanics, 1983(7): 727−734.

[6] Ali M, Ohioma E, Kraft F, et al. Theoretical, numerical, and experimental study of dynamic axial crushing of thin walled pentagon and cross-shape tubes[J]. Thin-Walled Struct, 2015(9): 253–272.

[7] FAN Z, LU G, LIU K. Quasi-static axial compression of thin-walled tubes with different cross sectional shapes[J]. Eng Struct, 2013(10): 80−89.

[8] ZHANG X, Hoon H. Crushing analysis of polygonal columns and angle elements[J]. Int J Impact Eng, 2010, 37(4): 441–451.

[9] CHEN W, Wierzbicki T. Relative merits of single-cell, multi-cell and foam-filled thin-walled structures in energy absorption[J]. Thin-Walled Struct, 2001, 39(4): 287−306.

[10] ZHANG X, CHENG G. A comparative study of energy absorption characteristics of foam-filled and multi-cell square columns[J]. Int J Impact Eng, 2007, 34(11): 1739– 1752.

[11] Nia A A, Chahardoli S. Mechanical behavior of nested multi-tubular structures under quasi-static axial load[J]. Thin-walled Structures,2016(9): 376−389.

[12] Baroutaji A, Gilchrist M D, Olabi A G. Quasi-static, impact and energy absorption of internally nested tubes subjected to lateral loading[J]. Thin-walled Structures, 2016(1): 337−350.

[13] 李健, 高广军, 董海鹏. 带隔板薄壁方管的耐撞性研究[J]. 中南大学学报(自然科学版), 2014, 45(7): 2481− 2488. LI Jian, GAO Guangjun, DONG Haipeng. Research on crashworthiness of thin-walled square tubes with diaphragms[J]. Journal of Central South University (Nature Science), 2014, 45(7): 2481−2488.

[14] Calladine C R, English R W. Strain-rate and inertia effects in the collapse of two types of energy-absorbing structure[J]. International Journal of Mechanical Sciences, 1984(6): 689−701

[15] ZHANG X, CHENG G D, YOU Z. Energy absorption of axially compressed thin-walled square tubes with patterns[J]. Thin-Walled Structures, 2007, 45(9): 737− 746.

[16] GUAN W Y, GAO G J, LI J, et al. Crushing analysis and multi-objective optimization of a cutting aluminium tube absorber for railway vehicles under quasi-static loading[J]. Thin-Walled Structures, 2018(2): 395−408.

[17] YU Y, GAO G J, DONG H P, et al. A numerical study on the energy absorption of a bending-straightening energy absorber with large stroke[J]. Thin-Walled Structures, 2018(1): 30−41.

On buckling mode and initial peak force control of thin-walled square tube under axial impact

YI Zhaofeng1, YU Yao2, GAO Guangjun2, LIU Dongliang1

(1. Technology Research Center, CRRC Tangshan Co., Ltd, Tangshan 063035, China;2. Key Laboratory of Traffic Safety on Track of Ministry of Education, School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China)

Based on impact experiments and virtual simulation tests, the mechanical response characteristics of square tube structure with diaphragms that can absorb energy were analyzed. The finite element model was established, and the explicit dynamic finite element ANSYS/LS-DYNA was used for numerical simulation. When compared with the experimental results, the relative error was less than 5%, thus verifying the validity of the numerical model. The experimental and simulation results show that the deformation mode is stably and reliably axisymmetric. Then, the influences of diaphragms and trigger structure on energy absorption characteristics were studied. It is concluded that more buckling folds are produced under the restraint of diaphragms, and the energy absorption increases by 17%. The induced structure has trivial effect on the overall energy absorption, but can significantly reduce the peak value of the initial impact force by 42.3%.

impact; energy absorbing structure; thin-walled square; trigger structure; diaphragms

10.19713/j.cnki.43−1423/u.T20191054

U270

A

1672 − 7029(2020)07 − 1841 − 08

2019−11−26

国家重点研发计划资助项目(2016YFB1200505，2016YFB1200404-03)；国家自然科学基金资助项目(51975588)

高广军(1973−)，男，河南安阳人，教授，从事列车撞击动力学研究；E−mail：gjgao@ csu.edu.cn

(编辑 蒋学东)