高速列车U型橡胶外风挡结构模态有限元计算与试验分析

蔡鉴明，张森，汪海燕，熊小慧，唐明赞

高速列车U型橡胶外风挡结构模态有限元计算与试验分析

蔡鉴明1,2，张森1,2，汪海燕3，熊小慧1,2，唐明赞1,2

(1. 中南大学 交通运输工程学院，湖南 长沙 410075；2. 轨道交通安全教育部重点实验室，湖南 长沙 410075；3.中车青岛四方机车车辆股份有限公司，山东 青岛 266111)

随着旅客列车运行速度的提升，安装在车厢连接处的U型橡胶外风挡结构在列车空气动力作用下产生变形振动，当气动载荷的激励频率接近外风挡结构固有频率时易引起共振现象。为分析U型橡胶外风挡结构固有动态特性，利用模态有限元计算和试验相结合的方法，比较有限元模态计算中2种材料本构模型的区别，并研究模态试验激励点与响应点位置对U型橡胶外风挡结构模态参数的影响。研究结果表明：有限元模态分析时，网格单元层数过少导致计算结果刚度偏大；采用Mooney-Rivlin本构模型计算橡胶材料模态参数相对于线弹性更为合适；有限元模态分析所得结构振型可为模态试验响应点位置的选择提供指导。研究成果可为高速列车U型橡胶外风挡结构设计提供参考。

高速列车；外风挡；U型橡胶结构；模态有限元分析；模态试验分析

U型橡胶外风挡结构作为高速列车重要组成部件，安装于两车厢端部连接处，如图1所示。其作用为使车体表面光顺平滑，减小列车运行时的气动阻力与气动噪声[1]。随着旅客列车运行速度的提升，U型橡胶外风挡结构在列车空气动力作用下产生变形及振动问题[2−3]。当气动载荷的激励频率接近外风挡结构固有频率时易引起共振现象，严重影响列车运行稳定性和乘客舒适性以及外风挡结构安全性。为防止高速列车特定运行条件下气动载荷激励外风挡共振，需要在U型橡胶外风挡结构设计时避开工作范围内的共振频率，因此对U型橡胶外风挡固有动态特性的研究显得尤为重要。目前针对U型橡胶外风挡的研究主要集中于对高速列车气动性能的影响以及橡胶材料工艺上[4−6]，其结构模态参数尚未有研究。结构的模态参数可通过基于有限元计算和试验方法的模态分析获得，随着模态分析技术的不断发展与完善，已在众多工程振动领域中广泛应用[7-8]。已有研究人员在高速列车车体及部件进行了结构固有振动特性分析。李旭娟等[9]针对1:8比例车体进行侧墙试验模态测试以及模态参数的辨识。张娇等[10]针对动车组齿轮箱损坏问题，对动车组齿轮箱进行有限元模态分析及试验模态分析。于金朋等[11]针对高速列车车体轻量化所带来的振动问题，对车体固有频率进行了分析研究等。而高速列车外风挡采用橡胶材料，其结构的固有振动特性尚未研究，以至于对外风挡振动问题的气动弹性分析及结构优化设计工作难以开展。本研究通过Abaqus软件建立U型橡胶外风挡有限元模型，采用线弹性和超弹性2种橡胶本构模型对U型橡胶外风挡试件进行有限元模态分析；利用PULSE LabShop平台对该试件进行试验模态分析，比较模态试验分析过程中响应点和激励点对该结构固有频率和模态振型的影响，并对模态试验与有限元计算结果进行相互验证。

图1 U型橡胶外风挡结构安装示意图

1 U型橡胶外风挡试件有限元模态 分析

高速列车外风挡在实际工作中，主要因车体表面与内、外风挡空腔之间形成的压差而导致外风挡受到垂直于车体表面方向的气动载荷。外风挡设计成U型结构其目的是为了使得结构质量较轻，同时又保证其横向刚度较大；并且U型结构在列车通过曲线时能够很好地为列车车厢之间提供相对位移量，保证列车良好的通过曲线能力。

1.1 有限元模态计算理论

在有限元模态计算中，通常将描述系统特征的运动方程组用矩阵形式表示为：

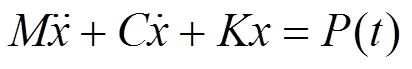
其中：为质量矩阵；为阻尼矩阵；为刚度矩阵，式(1)中表示有阻尼的个自由度系统的运动微分方程，当阻尼对结构的振型和固有频率影响不大时，可以忽略阻尼作用，无外力作用时则可将式(1)改为：

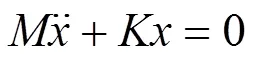
对无阻尼及外力作用时的运动微分方程，其微分方程有非零解的充分必要条件是系数矩阵行列式等于0，即特征方程：

通过对式(3)特征方程进行求解，可得到该系统的特征值，即固有频率、特征向量(模态振型)。

1.2 计算模型及离散化

为分析该U型结构橡胶外风挡的固有动态特性，利用高速列车上拆卸的外风挡部件进行试验研究，采用UG软件建立风挡试件的三维几何模型，并运用橡胶专用实体单元C3D8RH将其进行离散化。图2给出了U型橡胶外风挡试件实物、几何模型以及离散网格，模型高470 mm，侧壁厚度15 mm，圆弧顶部厚度6 mm，两侧壁宽度相距145 mm，U型凹槽深度245 mm。

图2 U型橡胶外风挡试件及计算模型

1.3 材料特性及边界条件

高速列车U型橡胶外风挡以EPDM(三元乙丙橡胶)为基材，通过一系列工艺处理得到U型结构。由于橡胶材料非线性、不可压缩性和大变形等特性，使得试验方法确定橡胶材料力学性能常数的过程繁杂。有限元分析和计算U型橡胶结构模态时，采用硬度换算输入橡胶材料的力学性能常数，该方法简便实用。图3为橡胶硬度与弹性模量的关系(国际橡胶硬度IRHD：虚线；邵氏A硬度：实线)[12]。

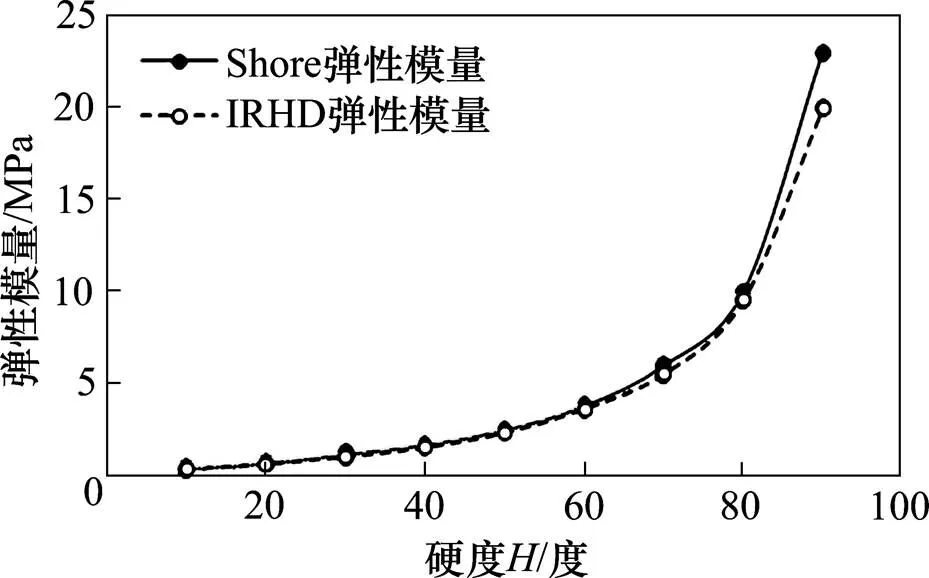
图3 橡胶硬度与弹性模量的关系

将邵氏A硬度与弹性模量之间的关系曲线分别采用指数函数、幂函数、对数函数拟合3个公式如下：

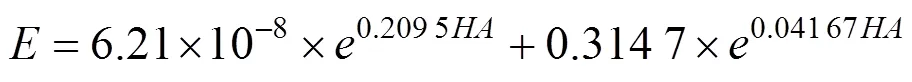
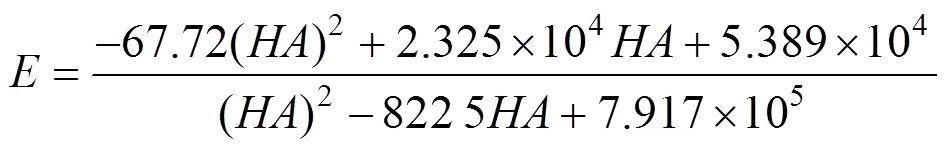
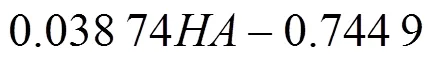
式(4)~(6)中：为橡胶弹性模量；HA为邵氏A 硬度。

如图4所示采用邵氏A硬度计对橡胶进行多次硬度测试实验，得到该U型橡胶试件的平均硬度，代入式(4)~(6)得到橡胶的弹性模量，取3个公式拟合结果平均值可以保证拟合的准确度。如表1所示，该U型橡胶外风挡试件的平均硬度为76 HA，平均弹性模量为8.03 MPa。

图4 U型橡胶材料硬度试验

表1 硬度换算弹性模量

在模态试验中，结构支承在安装框架上，有限元计算模型需要给定边界条件，其边界条件与模态试验所采用的U型橡胶试件安装方式一致，便于将有限元计算结果与模态试验结果进行比较分析。

为了得到准确的橡胶材料结构有限元模态分析结果，将该仿真结构进行了多次单元网格划分，比较不同单元网格层数对于计算结果的影响，并且通过橡胶材料的硬度换算得到橡胶材料的力学性能常数，采用线弹性模型和Mooney-Rivlin材料本构模型2种方法进行仿真计算，比较采用不同材料本构模型计算结果的区别。

1.4 线弹性模型

橡胶具有承受大的弹性形变的能力，但在实际应用中橡胶分子链往往只承受相当小的形变，因此当橡胶在小变形的过程中可将橡胶的应力−应变曲线关系简化为是线性的，则只需要输入橡胶材料的弹性模量值。

采用线弹性材料本构模型进行有限元模态分析时，在Abaqus中设置材料参数，弹性模量8.03 MPa，泊松比0.499 5，密度1 300 kg/m3。得到不同网格层数条件下U型橡胶外风挡试件的前3阶固有频率，如表2所示。不同网格层数条件下U型橡胶外风挡试件的前3阶固有频率会存在变化，随着网格层数增加，U型橡胶外风挡试件的各阶固有振动频率逐渐下降，当网格单元层数到达4层以后，计算网格单元层数对于固有频率的影响趋于平缓。由此可见，有限元模态计算时，对于U型橡胶结构的计算网格层数尽量增加到4层及以上较为合适。采用线弹性材料模型计算该U型橡胶外风挡试件结构的1阶固有频率为7 Hz左右，并且结构的第2阶和第3阶振动频率十分接近。

表2 线弹性模型下不同网格层数U型橡胶试件前3阶频率

图5中展示了当计算网格为2层时，该U型橡胶外风挡试件结构的前3阶振型图，更多单元网格层数的振型结果与2层单元网格计算结果一致。

通过图5(a)可以得知该U型橡胶外风挡结构试件的1阶振型是围绕固定边界做弯曲振动，而根据高速列车外风挡工作特性可以得知，外风挡受到垂直于车体表面方向(即垂直于U型侧壁方向)的气动载荷，因此外风挡结构受气动力产生外翻和振动主要为该结构的1阶振型，将该结构的1阶弯曲振动频率与工作范围内气动激励频率错开能够防止共振现象的产生。

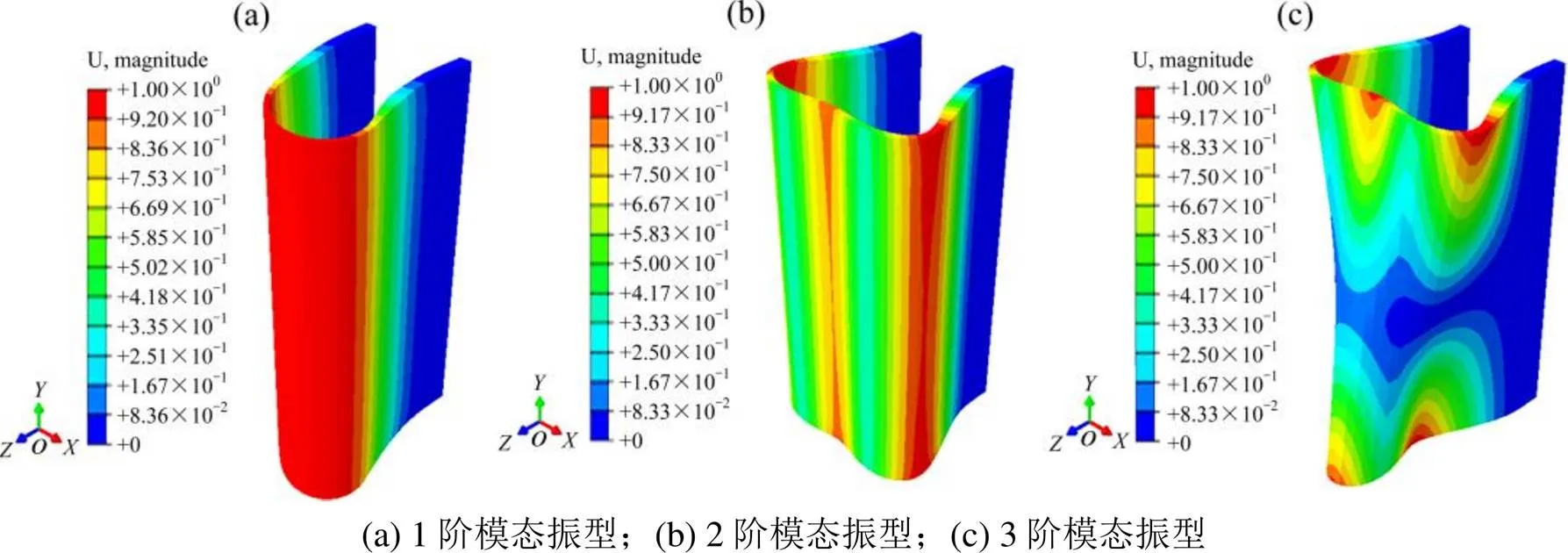
图5 有限元仿真模态振型

如图5(b)所示，该结构的2阶振型为圆弧顶部向内凹陷，圆弧与侧壁相切位置向外凸起，该振型类似于“M”形，而根据外风挡的应用情况可知，该结构的2阶模态振型则是影响列车通过曲线能力的主要振型，当列车通过曲线时，处于曲线内侧的2车厢表面相互靠拢，使得圆弧顶部对立的2块U型外风挡受到挤压，圆弧顶部向内凹陷，此振型与弧顶厚度以及侧壁厚度不同有关。

图5(c)中所示为该结构的第3阶模态振型，其结构一头为圆弧顶部向外凸起，圆弧与侧壁相切位置向内凹陷。一头为圆弧顶部向内凹陷，圆弧与侧壁相切位置向外凸起。

1.5 Mooney-Rivlin模型

橡胶是典型的超弹性材料，存在明显的非线性特征。在有限元方法中，常把橡胶近似视为不可压缩材料，使用超弹性本构模型描述其弹性能力，其中的Mooney-Rivlin本构模型在橡胶性能分析中较为常用。图6为邵氏A硬度HS与01/10的经验关系曲线，在橡胶小变形时，其弹性模量和材料系数的关系如下[13]：

式中：为橡胶弹性模量；01和10为Rivlin系数。

已知该结构材料硬度为76，弹性模量为8.03 MPa，根据图6中的经验关系曲线和式(7)求得01和10分别为1.507和0.018。在Abaqus中设置材料参数01和10，并输入密度1 300 kg/m3。采用Mooney-Rivlin本构模型对U型橡胶外风挡结构试件进行有限元模态分析。

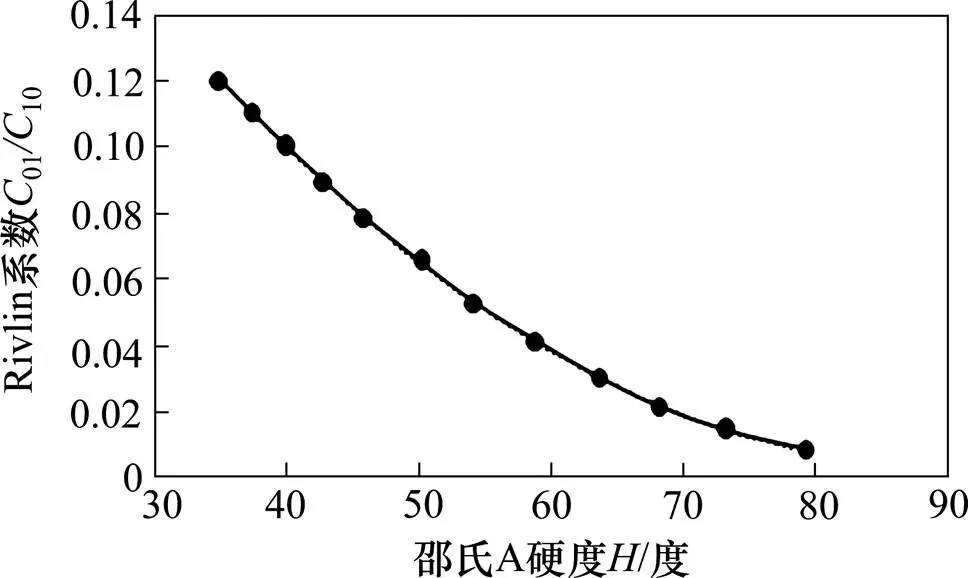
图6 邵氏A硬度与Rivlin系数C01/C10的关系曲线

如表3所示不同网格层数条件下U型橡胶外风挡试件的前3阶固有频率会存在变化。当计算网格单元为2层时，计算得该结构刚度较大，1阶固有频率达到7.89 Hz；当网格单元层数到达4层以后，计算网格单元层数对于固有频率的影响趋于平缓，网格单元层数达到4层时该U型结构的1阶固有频率为7.32 Hz，并且该结构的第2阶和第3阶振动频率十分接近。

利用该本构模型参数计算得到U型橡胶外风挡试件结构的前3阶振型与采用线弹性模型计算振型一致，见图5所示。

表3 Mooney-Rivlin模型下不同网格层数U型橡胶试件前3阶频率

对比表2和表3可知在固有振动频率上，相对于线弹性计算结果，采用Mooney-Rivlin本构模型计算的该U型橡胶外风挡结构试件振动频率较大。因为线弹性本构模型的应力应变关系通过广义胡克定律表述，是将复杂的非线性本构关系的线性简化。而Mooney-Rivlin本构模型应力应变关系通过应变能密度函数表述，应力应变关系是非线性的，更真实的反映出该橡胶材料应力应变关系，通过Mooney-Rivlin本构模型计算出结构的刚度相比于线弹性所求的刚度较大，因此计算的结构固有频率更大；在振型上，采用Mooney-Rivlin本构模型计算的振型与线弹性本构模型计算的结果一致，即采用2种本构模型计算所得特征值变化较大，而对于特征向量影响较小。

2 U型橡胶外风挡试件模态试验分析

2.1 试验平台

模态试验通过激振力与响应得到导纳函数确定结构的模态特征，如固有频率、振型和阻尼比，模态试验中的测试结果与结构的支承方式、响应点与激励点的选择以及试验系统的要求关系密切[14−16]。该模态试验针对于高速列车上拆卸下来的U型橡胶外风挡试件的固有振动特性进行研究。模态试验利用丹麦B&K公司开发的PULSE测量分析系统，采用LC0101E型加速度传感器，其质量为8，灵敏度为100 mV/g，使用频率范围为0.5~6 kHz，该型加速度传感器主要用途为模态试验。激励源采用LC13B系力锤，其参考灵敏度为0.1 mV/N，该系力锤在LC13系列力锤基础上，与电荷放大器集于一体，简化了测试系统，提高了测试精度和可靠性。该模态试验的测试系统如图7所示。

图7 模态试验系统

2.2 试验方案

本试验中对结构的支承方式采用刚性约束，固定方式与图1中高速列车U型橡胶外风挡结构的安装方式一致。测量试验的激励采用锤击法单点激励，在合适位置选取激振点进行多次测量，根据试验情况，每个激励点重复试验不少于3次。分析带宽为0~50 Hz，采样频率为512 Hz，频率分辨率为0.125 Hz。

为了分析模态试验响应点和激励点的选择对于该U型橡胶外风挡结构的模态参数的影响，采用了3种响应点布置和2个激励点位置选择的试验方案。图8给出了响应测点数分别为5，13和15时的测点布置，如图8(c)中星标所示，激励点位置选择在U型结构的圆弧顶部和侧壁位置，图9给出了在PULSE系统中建立不同响应测点的几何模型。

图8 不同响应测点布置图

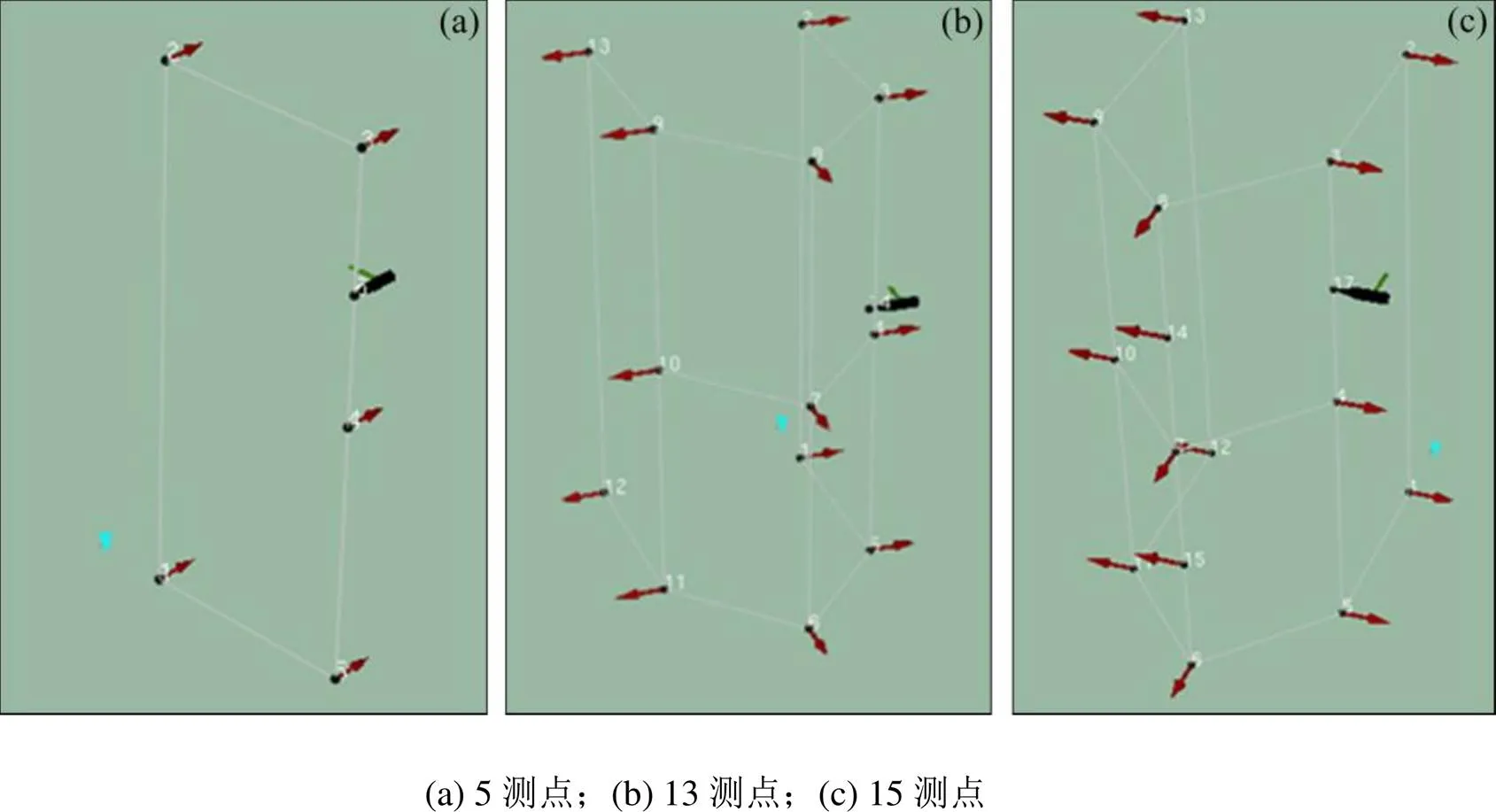
图9 不同响应测点几何模型

2.3 模态试验结果

通过多次模态试验，该U型橡胶外风挡试件的不同响应测点布置和激励点位置试验的前3阶固有频率如表4所示。当激励点位于侧部时，其响应测点数分别为5，13和15时该结构的前3阶振型如图10~12所示。

通过模态试验研究该U型橡胶风挡试件的固有振动特性，可以得出在该U型结构弧顶部位激励和侧壁位置激励对结构的固有频率及振型影响较小，各试验结果相近，证明试验具有重复可靠性。并且将5，13和15测点得到的实验结果两两对比，结果显示在5测点和13测点敲击弧顶区域时，第3阶频率试验结果偏差最大，为−5%；其次为5测点和13测点敲击侧壁区域时，第1阶频率实验结果偏差−4.3%，其余偏差绝对值均小于4%，可以说明加速度传感器和数据线的增加所带来的附加质量对于测试结果的影响在可接受范围之内。

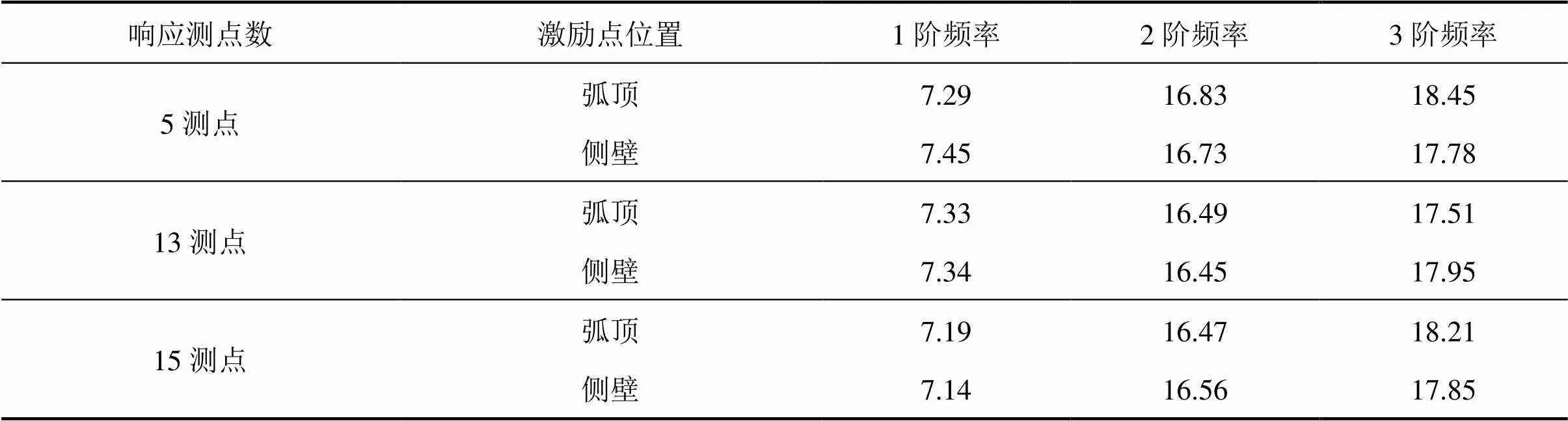
表4 模态试验结果

图10 前3阶振型(5测点)

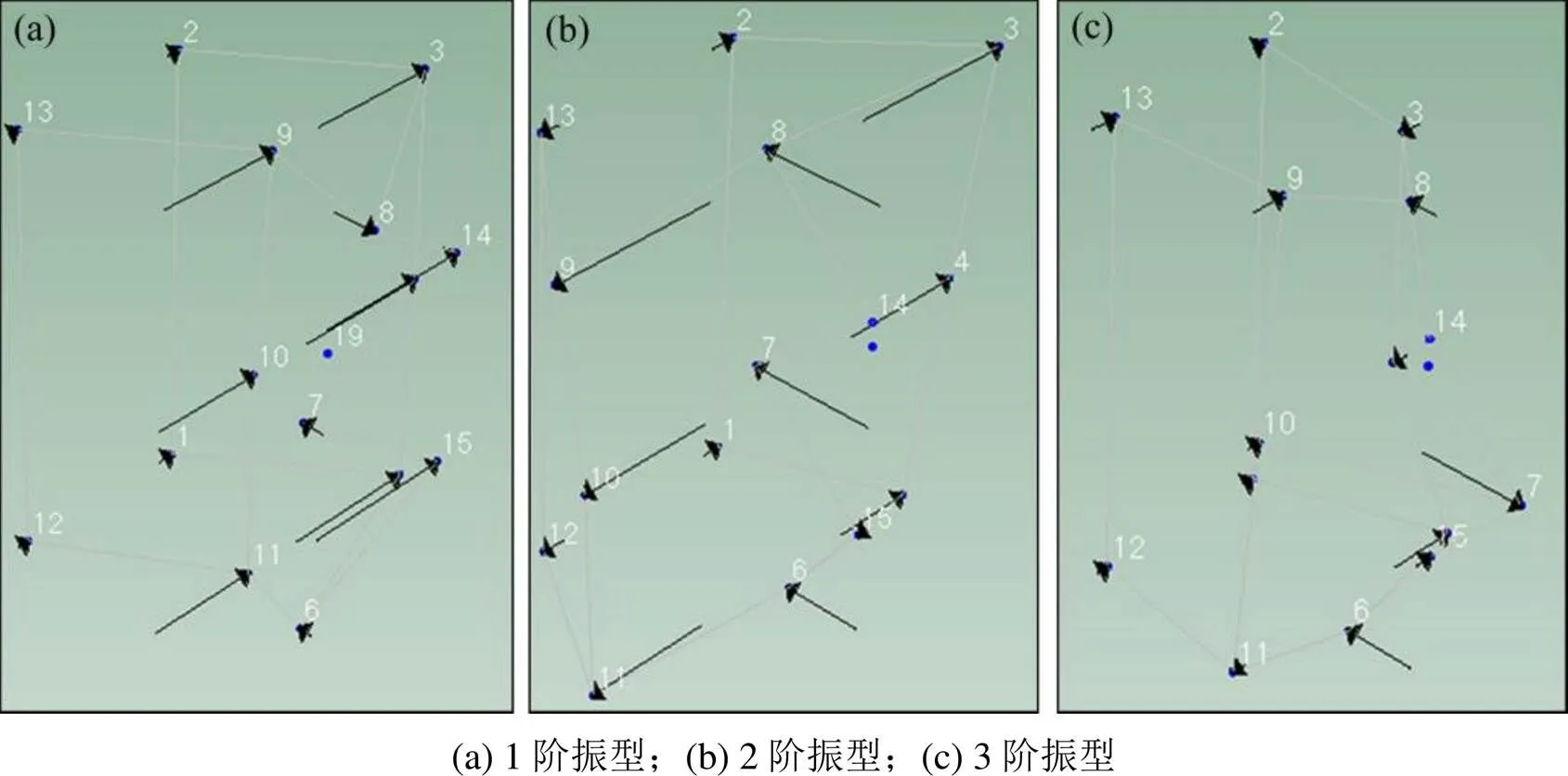
图11 前3阶振型(13测点)

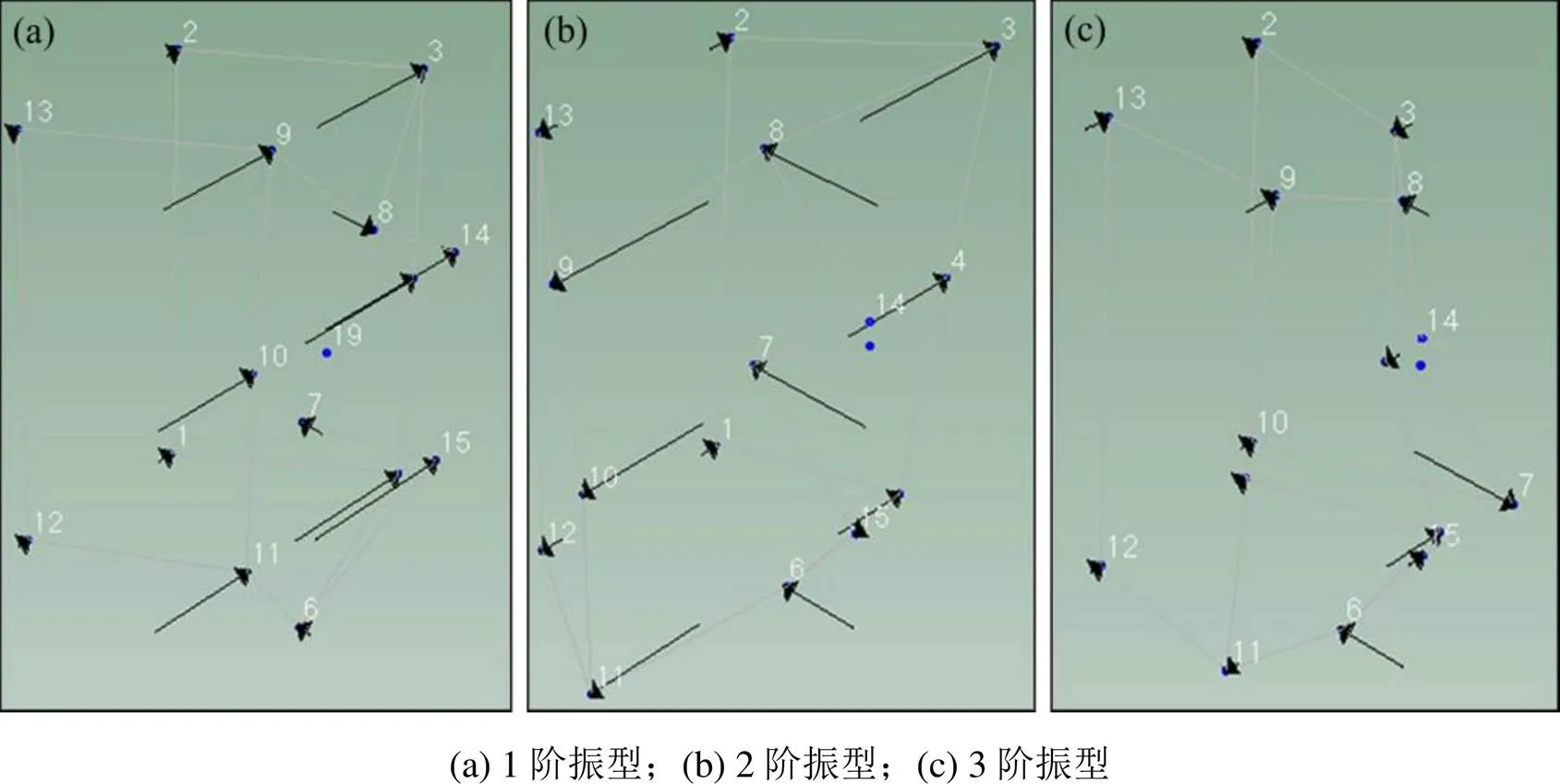
图12 前3阶振型(15测点)

当响应测点数为5时，只能显示出结构侧面的模态振型向量，属于测点数目过少。当响应测点布置在该U型结构几何特征位置时，即测点数增加到13测点，模态试验得到该结构的1阶振型是围绕固定边界做弯曲振动；2阶振型为圆弧顶部向内凹陷，圆弧与侧壁相切位置向外凸起，该振型类似于“M”形；第3阶模态振型，其结构一头为圆弧顶部向外凸起，圆弧与侧壁相切位置向内凹陷，另一头为圆弧顶部向内凹陷，圆弧与侧壁相切位置向外凸起，此时模态试验与有限元模态计算得到的振型一致。当响应点增加到15测点时，模态试验得到该结构振型与13测点时相同。

3 有限元模态计算与模态试验比较分析

表5给出了采用13个响应点在侧部激励的模态试验结果和采用4层计算网格2种构型的有限元模态计算结果及有限元模态计算结果相对于模态试验结果的误差。

对表5中的数据分析可知，采用线弹性材料模型计算该结构的前3阶固有频率相对于模态试验结果误差分别为−7.90%，−7.84%和−11.92%，采用Mooney-Rivlin材料模型得前3阶相对误差为−0.27%，−0.06%和−4.74%，采用Mooney-Rivlin材料模型计算得到结果相对误差较小。因此，在对橡胶外风挡进行有限元模态分析时采用Mooney- Rivlin材料模型更为适宜。

表5 U型橡胶外风挡试件固有频率比较

图13给出了有限元模态计算与试验模态结果中该结构的第2阶振型。从图中可以看出，2个振型几何特征位置处的模态特征向量方向一致，说明有限元模态计算与模态试验得到的该U橡胶结构的第2阶模态振型吻合。由图5和图11同样可得有限元模态计算与13测点试验模态结果中该结构的第1和第3阶振型几何特征位置处的模态特征向量方向一致，因此有限元模态计算与模态试验得到的该U橡胶结构的前3阶模态振型均一致。

图13 第2阶振型比较

4 结论

1) 有限元模态分析时，网格单元层数过少导致计算结果刚度偏大，随着网格层数增加，网格单元对于计算结果的影响趋于平缓。对橡胶结构在不同材料模型计算结果进行比较看出，Mooney-Rivlin本构模型用于计算橡胶材料模态参数更为适合。

2) 模态试验激励点位置的选择对于结构动态特性的影响较小，而响应点(测点)数量与位置对于结构动态特性的影响较大，在结构几何特征位置处布置响应点可以减少测点布置数量，简化测量。并且有限元模态分析得到的结构振型可为模态试验响应点的选择提供指导。

3) 模态试验与有限元计算结果相互验证，此研究提出的方法能够减少重复测试和经验判断带来的误差，并能够缩短设计周期，可为高速列车U型橡胶外风挡进一步优化设计和动力学分析提供参考依据，并使得有限元分析在未来橡胶外风挡产品开发中发挥重要作用。

[1] 王兴伟, 朱闰平, 缪惠勇, 等. 旅客列车风挡的发展方向[J]. 特种橡胶制品, 2014, 35(2): 79−84. WANG Xingwei, ZHU Runping, LIAO Huiyong, et al. The development direction of passenger train windshield[J]. Special Purpose Rubber Products, 2014, 35(2): 79−84.

[2] 唐明赞, 熊小慧, 钟睦, 等. 高速列车外风挡安装间距对风挡气动特性的影响[J]. 铁道科学与工程学报，2019, 16(4): 850−859. TANG Mingzan, XIONG Xiaohui, ZHONG Mu, et al. Influence of installation spacing of external vestibule diaphragm of high-speed train on aerodynamic characteristics of the vestibule diaphragm[J]. Journal of Railway Science and Engineering, 2019, 16(4): 850−859.

[3] NIU J Q, WANG Y M, ZHOU D. Effect of the outer windshield schemes on aerodynamic characteristics around the car-connecting parts and train aerodynamic performance[J]. Mechanical Systems and Signal Processing, 2019, 130: 1−16.

[4] 杨加寿, 蒋崇文, 高振勋, 等. 车厢间风挡形式对高速列车气动性能的影响[J]. 铁道学报, 2012, 34(11): 29− 35. YANG Jiashou, JIANG Chongwen, GAO Zhenxun, et al. Influence of inter-car wind-shield schemes on aerodynamic performance of high-speed trains[J]. Journal of the China Railway Society, 2012, 34(11): 29−35.

[5] 黄莎, 梁习锋, 杨明智. 高速列车车辆连接部位气动噪声数值模拟及降噪研究[J]. 空气动力学学报, 2012, 30(2): 254−259. HUANG Sha, LIANG Xifeng, YANG Mingzhi. Numerical simulation of aerodynamic noise and noise reduction of high-speed train connection section[J]. Acta Aerodynamica Sinica, 2012, 30(2): 254−259.

[6] 谭莲影, 苏韧伟, 黄良平, 等. 高速列车风挡用白色EPDM橡胶材料的研究应用[J]. 电力机车与城轨车辆, 2015(38): 98−101. TAN Lianying, SU Renwei, HUANG Liangping, et al. Investigation of white EPDM based vestibule diaphragm for high-speed train[J]. Electric Locomotives & Mass Transit Vehicles, 2015(38): 98−101.

[7] 马骊凕, 朱智民, 安占飞, 等. 轿车白车身模态分析[J]. 振动与冲击, 2013, 32(21): 214−218. MA Liming, ZHU Zhimin, AN Zhanfei, et al. Model analysis of a car BIW[J]. Journal of Vibration and Shock, 2013, 32(21): 214−218.

[8] HUA J, ZHOU S Z, WANG J Q, et al. Modal test and finite element analysis of sand blender’s agitator[J]. Advanced Materials Research, 2010(5): 39−141.

[9] 李旭娟, 缪炳荣, 史艳民, 等. 高速列车比例车体侧墙试验模态分析[J]. 机车电传动, 2017(3): 110−113. LI Xujuan, MIAO Bingrong, SHI Yanmin, et al. Experimental modal analysis of scaled car-body sidewall for high-speed vehicles[J]. Electric Drive for Locomotives, 2017(3): 110−113.

[10] 张骄, 高小平, 李熙, 等. 基于试验模态分析的某型号动车组齿轮箱有限元模态分析研究[J]. 机电工程, 2015, 32(7): 958−961. ZHANG Jiao, GAO Xiaoping, LI Xi, et al. Modal finite element analysis of an EMU gearbox based on experimental modal analysis[J]. Journal of Mechanical & Electrical Engineering, 2015, 32(7): 958−961.

[11] 于金朋, 张卫华, 孙帮成, 等. 高速车体结构参数对车体模态频率的影响分析[J]. 铁道学报, 2015, 37(9): 32− 37. YU Jinpeng, ZHANG Weihua, SUN Bangcheng, et al. Analysis on effect of structure parameters of high-speed car body on modal frequencies[J]. Journal of the China Railway Society, 2015, 37(9): 32−37.

[12] A.N.詹特. 橡胶工程—如何设计橡胶配件[M]. 张立群,等译. 北京: 化学工业出版社, 2002. Gent A N. Engineering with rubber—how to design rubber components[M]. ZHANG Liqun, et al, trans. Beijing: Chemical Industry Press, 2002.

[13] 王锐, 李世其, 宋少云. 橡胶隔振器系列化设计方法研究[J]. 噪声与振动控制, 2006(4): 11−13, 25. WANG Rui, LI Shiqi, SONG Shaoyun. Research on serialization design method of rubber vibration isolators [J]. Noise and Vibration Control, 2006(4): 11−13, 25.

[14] GB/T11349.3−2006, 振动与冲击机械导纳的试验确定第3部分: 冲击激励法[S]. GB/T11349.3−2006, Vibration and shock-experimental determination of mechanical mobility-Part 3: Measurement using impact excitation[S].

[15] Brian S, Patrick M, Mark R. ODS & Modal testing using a transmissibility chain[J]. Sound and Vibration, 2018, 52(2): 2−7.

[16] 王桂伦, 姜东, 周李真辉, 等. 铰接式空间桁架结构模态试验研究[J]. 振动与冲击, 2019, 38(12): 252−257. WANG Guilun, JIANG Dong, ZHOU Lizhenhui, et al. Modal experiment for a spherical hinged space truss structure[J]. Journal of Vibration and Shock, 2019, 38(12): 252−257.

Modal finite element calculation and test analysis on U-shaped rubber outer windshield structure of high speed train

CAI Jianming1, 2, ZHANG Sen1, 2, WANG Haiyan3, XIONG Xiaohui1, 2, TANG Mingzan1, 2

(1. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China; 2. Key Laboratory of Traffic Safety on Track, Ministry of Education, Changsha 410075, China; 3. CRRC Qingdao Sifang Co. Ltd, Qingdao 266111, China)

With the increase of the passenger train running speed, the U-shaped rubber outer windshield structure is installed at the joint of the train produces deformation vibration under the aerodynamic force of the train. When the excitation frequency of the aerodynamic load is close to the natural frequency of the outer windshield structure, it is easy to cause resonance. In order to analyze the inherent dynamic characteristics of the U-shaped rubber outer windshield structure, using the modal finite element calculation and the test method, the difference between the two constitutive models in the finite element modal calculation was compared, and the influence of the modal test excitation point position and response point on the modal parameters of the U-shaped rubber outer windshield structure was studied. The results are as follows. According to the finite element modal analysis, the number of mesh element layers is too small, resulting in a large stiffness of the calculation results. Using the Mooney-Rivlin constitutive model to calculate the modal parameters of rubber materials is more suitable than linear elasticity model. Choices of the location of the modal test response points can be guided by the resulting structural shape from the finite element mode. The research results can provide reference for the design of U-shaped rubber outer windshield structure of high-speed train.

high-speed train; outer windshield; U-shaped rubber structure; modal finite element analysis; modal test analysis

10.19713/j.cnki.43−1423/u.T20190922

U270.6

A

1672 − 7029(2020)07 − 1620 − 10

2019−10−20

中南大学研究生调查研究项目(2018dcyj049)；国家重点研发计划资助项目(2016YFB1200506-03)

蔡鉴明(1964−)，男，湖南长沙人，高级实验师，博士，从事交通运输组织与安全管控研究；E−mail：jmcai@csu.edu.cn

(编辑 阳丽霞)