从整体上把握好一章起始课教学——以“不等关系”的教学为例

许清清 杨海燕

(江苏省南京市第十三中学，210008

章建跃博士提出，要使课堂教学成为一个融数学知识、技能、思维、方法、思想和精神于一体的“整体性教学”.每一章的起始课都起统领作用,需要明确“是什么?”、“学什么?”、“怎么学?”本文以“不等式”一章的起始课——“不等关系”的教学为例,谈谈如何从整体上把握好一章起始课教学.

一、内容解析与学情分析

不等关系是两个量之间的一种数量关系,不等式是其数学符号表示,建模思想是蕴含其中的数学思想方法.

相等关系及其数学符号表示(等式),数学中某些不等关系及其数学符号表示(不等式),是本节课的逻辑基础.不等关系与相等关系都是两个量之间的数量关系,具有相似性,但不等关系中大小不同,所以两者又存在差异.

数学源于生活,用数学眼光观察世界,用数学思维分析世界,用数学语言表达世界,是不等关系中蕴含的基本思想和方法,在数学研究中具有基础地位,是学生发展“数学建模素养”的重要载体.

学生已知“相等关系”是一种数量关系,能用等式表示相等关系;已经历“寻找等量关系语句—列出等式—解方程(组)—实际问题的解—回答实际问题”的建模过程;已研究了等式相关性质，求解一元一次方程等方程的一般方法.学生积累了一定的建模经验,抽象概括等素养已得到培养.同时，学生已积累了一些数学中常见的不等关系,并会用不等式表示;了解不等式的构成、常见的不等号.这些为本节课的学习提供了知识储备和逻辑基础.

本节课的教学目标可确定为:

(1)借助具体情境,了解日常生活中存在着大量的不等关系;

(2)通过熟悉的数学中不等关系的数学表示—不等式,类比出生活中简单的不等关系的表示方法以及常见的不等关系词对应的符号表示;

(3)结合具体的实际问题,归纳总结出表示复杂不等关系的基本步骤以及常见的不等式模型,提升归纳概括能力;

(4)通过复杂的实际问题的解决过程(寻找不等关系语句—表示不等式—解不等式(组)—实际问题的解—回答实际问题),从中体会数学建模思想.

二、教学实录

1.感受不等关系

情境引入:月光诗会是十三中的特色活动之一,至今已举办了8年,在此活动中:

参会人数突破1 000人;

参会领导与评委介于8～12人;

当天气温最低16°,最高25°.

问题1从中你能看出什么样的数量关系?

师 这里参会人数的多与少,气温的高与低,…都反映了我们生活中一种常见现象—不等关系.

设计意图月光诗会活动是十三中盛大的活动之一,学生印象深刻,能够产生共鸣,调动学习积极性;能够感受到数学源于生活.

问题2你能举出一些生活中不等关系的例子吗?

设计意图调动学生的主观能动性,自主寻找身边的数学,发现数学.

师 在我们的生活中，不等关系普遍存在.

图1是我国春秋战国时期的一种取水器械——桔槔.同学们能说说其中蕴含的工作原理吗?

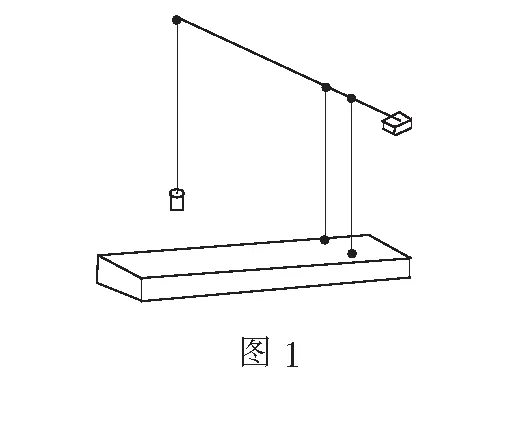
师 我们小时玩过跷跷板的工作原理也是如此.从上述问题可以发现,不等关系无处不在,而且在我们生活中有着重要的应用.这就是我们学习不等关系的原因.

设计意图结合玩具以及中国历史上典型的劳动工具,让学生感受到不等关系在实际生活中的应用,体会不等关系研究的重要性和必要性.

2.表示简单的不等关系

问题3你能举出数学中不等关系的实例吗?用数学符号如何表达?

问题4数学中的不等关系可以用不等式表示,那么生活中的不等关系是否也可以用不等式表示?

参会人数突破1 000人;

参会领导与评委介于8～12人;

当天气温最低16°,最高25°.

不等关系词突破介于…之间最低最高 不等式x>1 0008≤x≤12x≥16°x≤25°

追问你是怎样将文字语言的不等关系转化为符号语言的不等式的?

追问按此方法同学们能否写出所举生活中不等关系对应的不等式？

设计意图从数学中常见不等关系的表示过渡到生活中不等关系的表示,由抽象到具体,运用了方程的思想;在总结方法中感悟不等关系的表示,提高学生的抽象概括能力.

3.了解不等关系相关数学史知识

问题5有哪些常见的不等符号?

常见的不等符号有>、<、≥、≤、≠，用不等号连接的式子称为不等式.

数学史料记载,“不等号”是英国数学家哈里奥特(T.Harriot)于1631年开始使用的,但当时并没有被数学界所接受,直到100多年后,才逐渐成为标准的应用符号.

设计意图师生提炼概念,介绍数学史,感受数学文化.

4.表示复杂的不等关系，体会不等式的研究内容与研究意义

问题6刚刚我们用不等式表示了简单的不等关系,那么对于复杂的实际问题,如何用不等式表示其中的不等关系呢?

例1月光诗会的地点选在玄武湖,有同学提议在明城墙排练.明城墙的门票每位10元,20人以上(含20人)的团体票8折优惠,那么不足20人时应该选择怎样的购票策略?

提出系列问题:购票策略是什么?如何做到省钱?谁和谁比?这是什么不等式?

例2玄武湖设有多台自动售货机出售饮料.若某饮料以每瓶2元的价格销售时,月销售总量为10万瓶.经过调查,若价格每提高0.2元,月销售量就减少5 000瓶.若设每瓶饮料的定价提高x元,怎样才能使该饮料的月销售收入超过22.4万元?

提出系列差别题：哪句话体现不等关系?销售收入如何求?哪句话跟销售额有关?如何表示销售额?这是什么不等式?

例3师生晚餐由学校食堂提供营养快餐,它由甲、乙、丙三种食物混合而成(维生素含量及成本如下表):

维生素A(单位/kg)维生素B(单位/kg)成本(元/kg) 甲3007005 乙5001004 丙3003003

厨师欲将这三种食物混合成100 kg的食品,要使混合食品中至少含35 000单位的维生素A及40 000单位的维生素B,设甲,乙这两种食物各取xkg,ykg,那么x,y应满足怎样的关系?

提出系列问题1:哪句话体现不等关系?这是什么不等式?你能总结出解决实际问题的不等关系的一般步骤吗?列出不等关系后还需怎样才能解决实际问题?

设计意图在解决复杂的三个实际问题中,学生再次经历将不等关系用不等式表示的步骤,并归纳出其一般步骤;在解决问题的同时,认识三种常见的不等模型:一元一次不等式、一元二次不等式、二元一次不等式组,以及本章将要学习的内容:解一元二次不等式、线性规划.

5.回顾小结，感悟数学文化

问题7今天我们是怎样开展对“不等关系”研究的?你有何收获与感悟?

设计意图引导学生从本节课的研究路径出发,归纳本课内容,提炼思想方法,总结建模经验,形成表示不等关系的基本套路，解决实际问题的基本思路.学生在自主小结、相互补充中提升反思、归纳能力.

三、教学反思

1.用数学眼光观察世界,感受、感悟不等关系

不等关系在实际生活中普遍存在,它们让我们的生活多了趣味和韵味,巧用不等式能让生活变得轻松.如何引导学生用数学的眼光观察世界,发现、欣赏不等关系?

① 精心设计情境,以学生熟悉的活动——月光诗会(本校的特色活动之一)为主线,从简单的不等关系到复杂的不等关系;

② 选取学生喜欢的游戏——跷跷板、古代的劳动工具等实例,让学生感悟不等关系研究的必要性与意义;

③ 问题引领学生自主发现、合作交流,如“你能举出一些生活中不等关系的例子吗?”、“你能举出数学中不等关系的实例吗?”

2.用数学思维分析世界,建立不等关系的数学模型

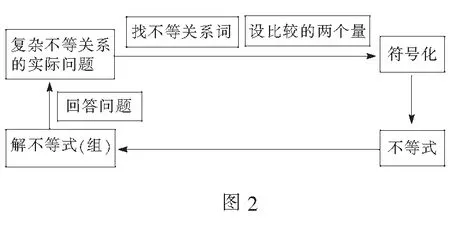
《新课标》指出,“数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养”.该数学案例设计问题串,搭建研究路径:从数学中常见的不等关系的表示类比出简单的不等关系的数学表示；寻找比较的两个量、设未知数、根据不等关系词列出不等式;对于复杂不等关系的实际问题,学生在操作体会的基础上,概括其思考方式和一般步骤,并进行迁移应用,最后形成如下思维导图(图2):

3.从整体上理解数学、理解学生、理解教学

“不等关系”是苏教版高中数学必修5第3章第1节内容.作为“不等式”一章的起始课,本节课在内容上有承上启下的作用,为一元二次不等式和二元一次不等式解法的学习埋下伏笔,有助于认识学习不等式的必要性和重要性.

学生是学习的主体,需要教师眼中有学生，心中有学生.创设学生熟悉的问题情境,呈现给学生刺激性的数学信息,引起学生学习的兴趣,激起其好奇心、发现欲. 教师在巡课的过程中及时发现学生的疑难点,并给予充分的指导:可以是私下交流,可以是学生相互纠正，可以是共同探讨,不轻易放过任何疑问,在轻松愉快的氛围中发展学生的思维.

数学教学是思维的教学,问题是数学的心脏.教师可以在问题教学的同时,塑造学生的思维,使学生的思维更加合理化、程序化,形成认识世界的一般方法与习惯.因此,笔者用“为什么要学习不等关系”,“你能举出一些生活中不等关系的例子吗”,“生活中的不等关系是否也可以用不等式来刻画呢”,“你能得到解决不等关系实际问题的一般步骤吗”等为学生营造一个又一个跌宕而自由的学习空间,让学生在不经意间进行发现、思考、类比、归纳,从而水到渠成地解决一个又一个的问题.