2019年自主招生数学试题选解
丁利娟 谢广喜
(江苏省无锡市青山高级中学,214036) (江苏省江南大学理学院,214122)
2020年初,教育部出台文件紧急叫停各高校的自主招生考试, 更新为更高级的 “强基计划 ”, 且每个省内的综合评价工作仍然存在. 对2020年即将迎来的各重点高校 “强基计划” 或“综合评价”考试,原来的自主招生考试试题仍有参考意义.本文筛选了一些去年的部分高校的自主招生数学试题,供参考.
一、以整数的基本性质为背景
这类问题注重初等数论的基础知识,通常只要想到奇偶性分析(有时也可能模3分类),知道质数、合数最基本的概念,再结合一些高中数学知识(比如二项式定理),很多问题就可以迎刃而解了.当然,知道同余的概念会大大缩减我们解题的书写过程.
例1(2019年浙大自主招生题)已知p(n)为n次的整系数多项式,若p(0),p(1)均为奇数,则( )
(A)p(n)无整数根
(B)p(n)可能有负整数根
(C)p(n)无解
(D)以上答案都不对


综上,选A.
例2(2019年清华大学自主招生题)设a为4 4444 444各位数字之和,b为a各位数字之和,c为b各位数字之和,求c的值.

由4 444≡7(mod 9),可得4 4444 444≡74 444(mod 9)=(73)1 481·7≡1×7=7(mod 9),进而有a≡b≡c=7(mod 9).
下证c≤12.
注意到4 444×3=lg1 0004 444 由1≤c≤12,结合c≡7(mod 9),得c=7. 评注本题源自第17届国际数学奥林匹克试题. 自主招生考试的复数问题通常高于中学教材的要求,有一定的难度. 评注本题为复数模背景下夹逼法的运用.无独有偶,今年的北京大学自主招生有一道题的解题要害与本题非常相似,只是知识背景是实数而已. 评注本题需用待定参数法,结合不等式取等号条件将y2按比例分拆开. 评注这道题其实是2011年清华等七校联合招生“华约”试题. 分析本题最常用的办法是用正弦定理及和差化积求解,考虑到和差化积内容超出高中考核要求,我们换一种思路,利用图形,结合三角形面积公式求解. 解如图1,记∆ABC的内切圆半径为r,由海伦公式,有 例7(2019年浙江大学自主招生题)已知∆ABC的顶点A(-p,0),B(p,0),其内心在直线x=q上,且p>q>0,则顶点C的轨迹方程为______. 解利用内心基本概念,易知顶点C的轨迹在双曲线上,且该双曲线两焦点就是A(-p,0),B(p,0),即半焦距c=p,半实轴a=q,所以顶点C的轨迹方程为 评注本题网上答案有误.二、以复数为背景





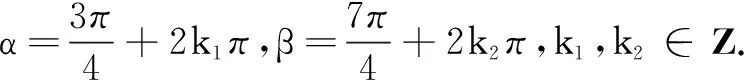
三、以不等式为背景问题
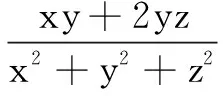
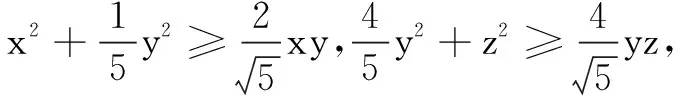
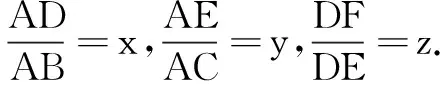

四、以三角函数为背景



五、以圆锥曲线概念为背景

