涡轴发动机弹性支撑外挤压油膜涡动特征频率*

林学森， 李本威， 王景霖， 张 赟， 康冰冰

(1.海军研究院 北京，100161) (2.海军航空大学航空基础学院 烟台，264001)(3.故障诊断与健康管理技术航空科技重点实验室 上海，201601)

引 言

涡轴发动机作为航空器重要的动力机械，通常比涡扇、涡喷发动机具有更高的转速和更细的转动轴，且通过减速齿轮等传动部件对外输出功率，因此，其发动机整机振动问题更为突出。在发动机台架试车测振过程中，由于涡轴发动机内部存在气体、转子、齿轮、轴承、油膜、密封及刮磨等多个激振源，各激振源间有耦合、调制作用，导致其频域范围带宽大、峰值多，较难找到对应频率分量。当前，航空发动机多采用带定心弹支的挤压油膜阻尼器，其动力学特性更为复杂，对整机的振动响应影响也尤为突出，并且受发动机内部空间结构的限制，很难采用电涡流传感器等手段监控其轴心运动轨迹等动力学特征。因此，如何通过机匣外振动传感器提取并识别挤压油膜阻尼器的特征频率具有十分重要的意义。

挤压油膜阻尼器以其卓越的减振性能被广泛应用到航空发动机上，特别是对转子过临界转速时的振动响应控制十分明显，有大量的学者对其动力学特性展开深入研究，取得了一系列成果。邓吟等[1]利用有限元法对挤压油膜阻尼器中的油膜动力特性进行研究，得出与Π油膜理论趋势一致的结果，并且在考虑惯性力后，随转速增加油膜压力及阻尼也增大。San等[2]通过研究多个连续冲击载荷时挤压油膜阻尼器-弹支结构的响应，证明了精确制造保证油膜间隙的重要性。文献[3-4]通过短轴承理论研究不同偏心率、不同动静载荷下发生瞬态变化时挤压油膜阻尼器(squeeze film damper，简称SFD)对转子振动响应的控制能力，并通过实验进行了验证。Sattipalli等[5]给出了一种通过非线性SFD耦合转静子系统的频率响应方法，该方法可以有效预测发动机静子结构的振动响应问题。祝长生等[6]通过柔性转子-挤压油膜阻尼器实验测量得到轴心轨道的非协调涡动，并且测得在油膜间隙较小情况下产生的带有单内环的非协调涡动轨道的进动频率约为转子转速之半，即1/2阶亚协调涡动。单独针对油膜特征频率提取的文献多见于滑动轴承，如罗宏林等[7]所述。

由于航空发动机实测振动信号包含有大量噪声及不同的调幅、调频因素，因此对振动测试数据的处理尤为重要。当前对该类非平稳信号的处理方法有小波变换、魏格纳-威利分布及独立分量分析等，但其在工程应用中会出现各种问题，如小波变化中小波基是确定的，整个分析过程无法更改，导致分析精度依赖于小波基的选择等。而经验模式分解(empirical mode decomposition，简称EMD)作为一种自适应的时频分析方法，在旋转机械振动信号处理领域有较好的应用效果。文献[8-10]利用EMD方法采集信号进行滤波，有效提取到了所关注的目标信号。同样的，EMD方法针对非平稳、非线性信号可以同时反映其时域与频域信息的特点，能较为显著地表达振动信号成分并进行较为准确的故障诊断[10-12]。

综上所述，为了对涡轴发动机整机状态下的定心弹支机匣油膜阻尼器频率特性进行分析，要综合挤压油膜阻尼器动力学特征、发动机振动源梳理与振动信号特征提取等多方面理论，才能得出较为准确的分析结论。

1 某型涡轴发动机整机振动信号采集的分析

某型涡轴发动机主要气路转动部件由离心压气机、燃气涡轮及自由涡轮组成，其中离心压气机叶轮与燃气涡轮转子之间采用圆弧端齿连接，用压气机轴拉紧，并通过压紧螺母压紧，使之成为整体的联合转子。在整机测振时，采用某进口高频响、高温加速度传感器，为了兼顾较高的分析频率(尽量采集到主要转动部件的2，3倍频)和振动响应幅值的精度，本次实验采集频率为10 kHz，分析频率考虑车台部件谐振点及气动低频干扰采用150 Hz～3 kHz。为保证测试精度和避免系统误差，采用同一机匣不同安装位置的双传感器进行对比。

1.1 试车测振信号的经验模态分解

将采集的振动信号进行频谱分析后，除了能够观察到转子的基频及倍频外，还存在有大量弱小的峰值响应，其对应的物理意义并不明确，也经常被忽略。因此，采用一种自适应的时频局部化分析方法，即EMD，其分解出的前几个本征模态函数分量往往集中了原信号中最显著、最重要的信息，这有助于发现发动机复杂激振源中容易被忽略的部分。采用进行发动机振动信号分析的步骤如下：

1) 选取适当长度的发动机稳定工况试车测振数据，为保证计算精度与计算效率，本实验采用x(t)为50k离散点作为计算样本；

2) 确定样本信号x(t)的所有局部极值，并通过3次样条插值函数将所有极值拟合成原始数据样本的上、下包络曲线；

3) 将样本信号x(t)减去上、下包络曲线的均值m1(t)，可得到一个去掉低频的新数据序列h1(t)

h1(t)=x(t)-m1(t)

(1)

4) 验证所得h1(t)是否为本征模态函数imf，即验证h1(t)是否极值数目和过零点数目相等或仅相差1，上、下包络线计算出来的局部均值是否为0；

5) 若h1(t)满足imf的两个条件，则h1(t)是第1个imf分量；若不满足，则重复步骤2和3，如式(2)，得到h1k(t)满足imf基本条件，记作a1(t)=h1k(t)

h1k(t)=h1(k-1)(t)-m1k(t)

(2)

6) 从原始信号x(t)中减去a1(t)，得到剩余信号为

r1(t)=x(t)-a1(t)

(3)

7) 通过对发动机激振源的转频分析，并结合分析频带要求，通过多次实验，发现对于该型涡轴发动机，仅需关注前7个imf分量即可，因此，当计算得出a7(t)时计算停止。

通过以上步骤，计算得出的原始样本x(t)的前7个本征模态函数imf如图1(a)所示。为更好地显示其特征，本研究仅截取稳定工况的前2k数据点进行展示。EMD分解方法主要目的是从复杂信号中获得有意义的瞬时频率，但是分解得出的本征模态函数需要人为结合被测对象解释其物理意义。由于分析频率包含转子3倍频，因此分解后高频分量占据imf的前4阶。从第5阶imf的时域尺度和其对应的傅里叶频域可以清晰提取出燃气发生器联合转子与自由涡轮基频的组合振型及其频域特征，如图1(b)所示。然而对于第6阶imf，却有一个明显的中低频峰值，不能很好解释其激振源位置，因此将其作为重点研究对象进行进一步探讨，如图1(c)所示。

在两组患者入院之后,均采取监测血压、心电图监护以及吸氧等基础护理。同时将尿激酶1.5万U与生理盐水100ml均匀混合,并给予患者静脉滴注,并保证滴注在30min之内完成。对于对照组在入院当天给予300mg的氯吡格雷,采取口服治疗,第二天减量至75mg;而研究组则采用氯吡格雷联合阿司匹林进行治疗,即在对照组治疗的基础上给予300mg的阿司匹林,次日则可减量至氯吡格雷75mg,阿司匹林100mg。

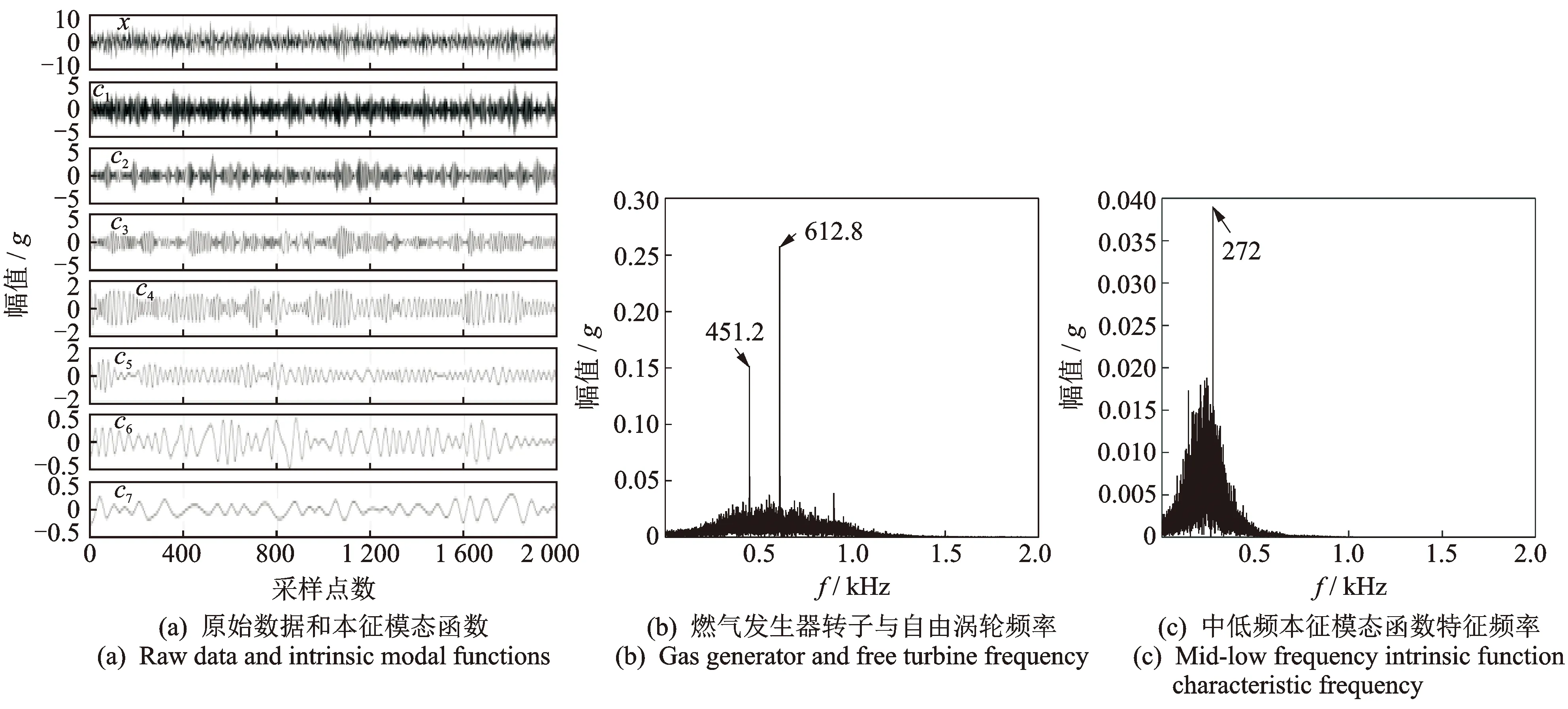
图1 EMD方法分析结果Fig.1 The results for EMD analysis

1.2 稳态工况亚同步特征显示

由于EMD分解方法是为了在幅值解调分析时将相位信号求导得出的瞬时频率表达出来，然而在发动机实测信号中每个瞬时频率包括多个激振源的振荡模式，因此EMD算法采用了多个单一振荡模式的分量的线性叠加，因此EMD分解多处理时间尺度较小的原始数据。为了更好地研究所发现的中低频峰值信号，取该稳态状态(状态1)中间段的实验数据(150～250 s)进行分析。由于该频率为低频，所以为提高计算效率，将分析频带调整为2 kHz以下，所得的时频图像如图2(a)所示。图中GF为燃气发生器转子频率，FF为自由涡轮频率，2GF和2FF分别为对应的2倍频，OF频率为低频信号。由图可以看出，OF频率在低频范围较为显著，且在稳定状态频率与幅值稳定，因此判定其为某一亚同步转速。

图2 发动机稳定状态时频图Fig.2 Time-frequency graph in engine steady condition

为验证其为亚同步跟随频率，取发动机状态2的稳态工况数据进行验证，所得到的时频图像如图2(b)所示，其结果与状态1规律一致。进一步计算其各频率间关系可以得出，OF频率与GF频率间存在0.443倍的比例关系，如表1所示。为了消除传感器带来的误差，表1中列出了采集自发动机同一截面不同传感器的频率分量对比，可以看出该型传感器精度与一致性好。

表1 OF与GF比例关系

2 亚同步频率激振源分析

经发动机多状态验证，表明存在某一特征频率与燃气发生器转子频率存在恒定的0.443倍关系，且该频率与燃气发生器转子频率同步性高，因此其可能为某调制因素导致或由特定的激振源激发。

2.1 激振源频率特征筛查

参考文献[13-14]，可以梳理出0.443倍转子基频所有可能的振源类型，如表2所示。

表2 激振源特征频率梳理表

对于碰磨，由于未见时频图像出现边频带现象，且将发动机进行分解检查时未见明显的刮磨痕迹，所以排除该因素。对于密封、压气机叶轮间隙及涡轮间隙激起的涡动，由于其与负荷相关，在发动机改变运行状态时，其特征频率可能发生变化，但由于无法对其进动状态进行测量，所以暂时排除，将结合下一步断滑油实验进行最终排除。滑动轴承半速涡动与实验中发现的特征频率符合度高，但是目前文献对象均为滑动轴承，而该型涡轴发动机未采用滑动轴承，故排除。鼓筒段或转子内腔有滑油渗漏积液现象，属于故障情况，通过发动机分解检查和多台发动机试车测振予以排除。因此，确定该特征频率为某一调制频率或某一新激振源的可能性大。调制频率可通过后续断滑油实验予以排除，该激振源频率参考滑动轴承半速涡动现象，初步分析为燃气发生器联合转子前定心弹支外挤压油膜涡动导致。

2.2 挤压油膜涡动频率探析

当前航空发动机普遍采用挤压油膜阻尼器来减小转子通过临界转速时的振动和经过轴承向外传递的载荷，设计优化的挤压油膜阻尼器能减少60%以上的外传响应，并且能够抑制转子系统的不稳定性和具有承受一定转子突加不平衡载荷的能力。然而，有关挤压油膜阻尼器的一些机理至今仍未完全弄清楚，还不能根据设计参数来精确计算阻尼器性能[13]。同样，对于阻尼器由于油膜反力带来的挤压油膜阻尼器特征频率也少有研究。该型涡轴发动机燃气发生器联合转子的前支承为带有定心弹支的挤压油膜阻尼器组件，其结构如图3所示。

图3 挤压油膜阻尼器结构Fig.3 The structure of squeeze film damper(SFD)

由于定心型挤压油膜阻尼器内环为弹性支撑，其另一端通过螺栓连接在机匣处，整体而言其为非旋转件。然而在机匣径向截面上看，弹性支座受内部转子轴颈转动的挤压，在截面上做圆周晃动，因此参考文献[15]中滑动轴承的油膜涡动频率提取方法对挤压油膜的涡动频率进行分析，如图4所示。

图4中，外圆为发动机内机匣限位器，内圆为弹支外圈，内外圆之间为挤压油膜。由于内圆在平面内做圆周晃动，因此在单位时间dt内，A′和B′点处的线速度可等效为内圆自转线速度的效果，圆周晃动可等效为类自转运动，类自转角速度为ω′。由于油膜具有不可压缩性，因此当内圆在外圆内做偏心转动时，形成一个进口截面AA′大于出口截面BB′的油楔，对于涡轴发动机这种高速轻载转子，内圆表面的线速度很高而载荷较小，此时内圆从AA′带入的油量大于从BB′带出的油量，多余的油将推动内圆前进，形成与内圆类旋转方向一致的涡动运动，涡动速率即为油楔本身的前进速率Ω的一半左右。

图4 挤压油膜涡动频率分析Fig.4 Oil whirl characteristic frequency analysis

在内圆作类旋转运动时，由于油膜具有黏性，所以在A′与B′处速度与内圆类旋转线速度相同，均为rω′，而对应的外圆上A与B点油膜速度为零。为方便计算，间隙中的油膜运动速率呈线性分布。图中月牙阴影面积为内圆在dt内掠过的面积，这部分面积等于油膜在进出口间隙的流量差。假设油膜宽度为l，内外圆平均间隙为C，偏心距为e，油膜两端的泄漏量为dQ，根据流体连续性原则，可得

解得

Ω=(0.42～0.48)ϖ′

(6)

与前者通过实验发现的0.443倍关系吻合度高。

3 挤压油膜涡动特征频率实验验证

为进一步排除压气机叶轮间隙、涡轮间隙和密封产生的涡动频率及调制因素，确定油膜在特征频率中的主导因素，特进行发动机断滑油实验。

3.1 实验设计

结合GJB 242A—2018《航空涡轮螺桨和涡轮轴发动机通用规范》中对发动机滑油流量中断的工作能力和实验验证要求，设计进行发动机稳定状态下滑油中断实验，其原理如图5所示。实验步骤为：

1) 将发动机保持在稳定状态，进行台架测试，确保发动机运行稳定无异常，传感器与采集设备正常；

2) 打开通气断油电磁阀，瞬间降低滑油进油压力至标准大气压力一半以下，并向滑油泵进口通气；

3) 保持发动机在该稳定状态运行30 s后切断电磁阀恢复供油，监控发动机性能与振动限制值在标准范围内；

4) 停车后进行滑油光谱分析和发动机分解检查，确定在断滑油运行过程中发动机无结构损伤等异常；

5) 全程进行振动参数测量，实验后进行振动参数分析。

3.2 实验结果分析

将实验过程的前后60 s实验数据作为分析样本，作出时频图如图6所示。由图中可以清晰看出，燃气发生器、自由涡轮转子频率响应在断滑油后变化不明显；然而OF频率响应由于无滑油供应，油膜消失，所以该频率响应在断滑油后瞬间消失，后续偶尔出现的微弱响应为滑油腔室内残存的少量油液导致。这也进一步证实了前者关于OF频率为挤压油膜涡动频率的推论。

图6 断滑油过程时频图Fig.6 Oil interruption course time-frequency graph

另一方面，稳态断滑油实验过程中，由于发动机转速、空气流量、压比及功率等发动机性能条件均未发生变化，因此OF频率的变化与压气机叶轮间隙、涡轮间隙及密封等激起的涡动无关，也与其他调制因素无关。

4 结束语

利用EMD方法对某型涡轴发动机的台架测振参数进行分析，在前几阶本征模态函数中发现有某个中低频分量的激振源暂不明确。通过选定合适的参数作出发动机稳态时频图像，证明该信号为一亚同步频率，并利用多传感器、多状态测量，确定该频率与燃气发生器转频之比为0.443。经过对挤压油膜涡动频率机理的计算与断滑油实验排除其他干扰因素后，确定该频率为该型发动机燃气发生器联合转子前定心弹支外挤压油膜阻尼器的特征频率。由于该频率在发动机运行过程中始终存在，因此在发动机设计与使用时，应避免发动机各主要工况下该油膜涡动频率与转子临界转速以及部附件的固有频率重合或相近，从而发生自激振动，引起转子系统失稳或部附件疲劳损坏。