基于CARMA 模型的动力电池荷电状态估计

黄玉莎，陈玉珊，秦琳琳，石 春，吴 刚

（中国科学技术大学 信息科学技术学院，安徽 合肥 230026）

0 引言

锂离子电池作为能量存储部件，凭借其高效、环保等优势在电动汽车行业被广泛应用[1]。电池自燃、碰撞后爆炸等安全性问题的发生也警示我们，锂离子动力电池及其管理技术尚未完全成熟[2]。准确建立电池模型并估计荷电状态(state of charge，SOC)，有利于了解电池剩余容量，实现电池的有效监督和管理[3]；但由于电池的非线性时变特性，以及放电过程中电池内部复杂的电化学反应，SOC 无法直接被测量得到[4]。

SOC 通常被表示为电池剩余容量与当前容量之比。常用的SOC 估计方法包括：

（1）安时积分法，即对电流积分得到电池充放电容量，结合初始SOC 计算当前SOC，该方法简单易行[5]，但由于采用开环预测，受初始SOC 及电流测量精度影响较大，易产生累积误差。

（2）开路电压法，即利用开路电压（open circuit voltage，OCV）与SOC 之间的对应关系，借助电池OCV 确定其SOC，不存在累积误差和初值问题[6]。考虑到在汽车实际行驶过程中无法通过长时间静置得到电池OCV，多采用其他方法确定电池OCV，再结合开路电压法计算电池SOC[7]。

（3）扩展卡尔曼滤波法[8]或无迹卡尔曼滤波法等。该方法多取OCV 或SOC 作为状态变量之一，控制变量为可测的电池端电压，算法的准确性受电池模型及初值选取影响较大，但闭环的卡尔曼滤波算法可以通过端电压测量值与预测值的差值变化反馈调节SOC估计误差，不存在累积误差。

（4）神经网络算法。该方法多以电池电压、电流和温度作为输入层，输出层为电池SOC，大量数据训练后估算较为准确[9]，但训练过程对计算机性能要求较高，仅利用整车上单片机来实现较为困难。

本文基于马里兰大学三元石墨锂电池单体实验数据，考虑到OCV-SOC 曲线在SOC 低、中、高区间会呈现不同变化趋势，为提高建模精度、降低模型阶次，分段建立OCV-SOC 模型；为确定电池OCV，假设扰动为平稳随机过程，建立电池受控自回归滑动平均模型(controlled auto-regressive moving average，CARMA)，推导得到OCV 最优估计值，并将其代入OCV-SOC 模型以实现电池SOC 估计。

1 动力电池建模与参数辨识

本文所进行的动力电池建模分为非线性静态环节建模和动态环节建模，即分别建立电池OCV-SOC 分段模型和CARMA 模型。

1.1 OCV-SOC 分段模型

低电流OCV 测试和增量OCV 测试是确定电池OCV-SOC 静态非线性关系较为常用的方法。郑方丹等人的研究进一步表明，基于增量OCV 测试预先确定OCV 和SOC 之间的关系，在进行SOC 在线估算时具有更高的估算精度[10]。据此，本文采用25 ℃下增量OCV 测试数据建立电池OCV-SOC 模型，利用试验过程中充、放电电量计算得到电池SOC，并认为静置2 h 后电池的端电压为该SOC 下的OCV；同时，为降低充放电曲线之间滞后效应的影响，取充放电过程中同等SOC处的OCV 平均值为开路电压值，利用Matlab 拟合得到图1 所示3 条OCV-SOC 曲线。

综合建模精度以及SOC 估计效果，本文根据放电 过 程OCV(voc)和SOC 数 据，按0＜SOC≤0.2、0.2＜SOC≤0.6、 0.6＜SOC≤1 分成3 个不同区间；利用Matlab 中polyfit 命令进行多项式拟合，得到OCVSOC 分段模型，具体如式（1）所示。为方便拟合，本文取voc1=voc-3。

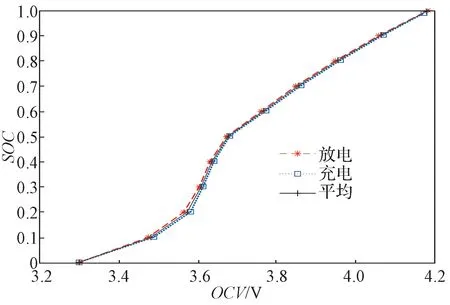
图1 OCV-SOC 曲线Fig.1 OCV-SOC curves

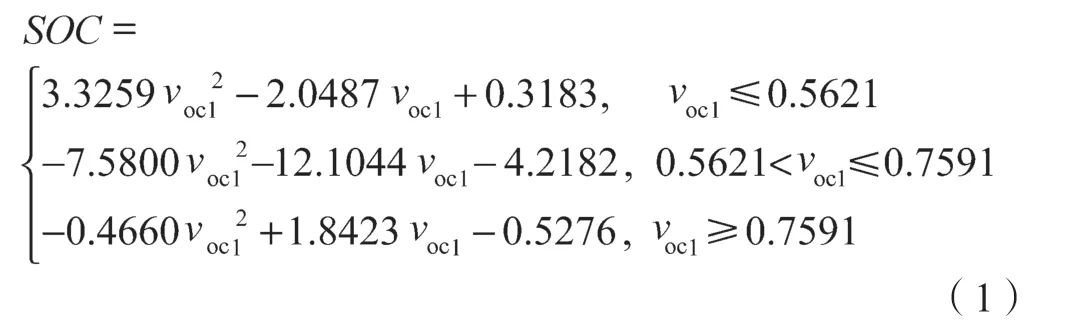
OCV-SOC 分段模型的拟合效果及其误差如图2所示，图中虚线表示模型分段点。在各OCV 点，估计SOC 的最大绝对误差为1.97%，误差平均值为-0.012%，均方根误差（root mean square error，RMSE）为0.72%；未分段建模情况下，模型最高阶次需达到7 次，才能实现各OCV 点处SOC 的最大绝对误差为1.91%，RMSE 为0.94%。分段建模在保证建模精度的同时有效降低了模型阶次。

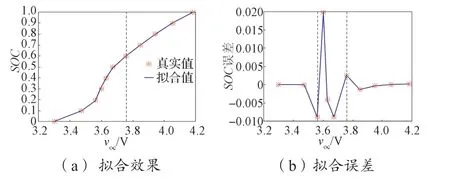
图2 OCV-SOC 分段模型拟合效果与误差Fig.2 Fitting effect and error of the OCV-SOC segmentation model

1.2 CARMA 模型

常用的电池模型中，由于电动汽车上单片机性能限制，神经网络模型较少被用于整车的电池SOC 估计；电化学模型能够比较准确而具体地描述电池内部的反应机理，但涉及耦合的时变偏微分方程，计算过程复杂且参数难以被辨识，更多用于电池设计；等效电路模型用电压源、电阻和电容等描述电池的电性能，虽然无法反应电池作用机理，但模型简单直观、参数易于辨识，适用于电池SOC 估计。何洪文等为锂离子电池构建不同阶RC 网络模型，仿真结果表明，利用一阶和二阶RC网络建立电池等效电路模型，在估计电池SOC 时可以更好地追踪真实值，其中二阶RC 等效电路模型的精度更高[11]。综合考虑模型精度和计算能力，本文选用如图3 所示的二阶RC 等效电路模型，图中R0为欧姆内阻，R1和R2为极化电阻，C1和C2为极化电容，I(t)表示t时刻端电流，x(t)和x′(t)分别表示t时刻R1C1和R2C2两端的电压，v(t)表示t时刻电池开路电压，u(t)表示t时刻端电压。

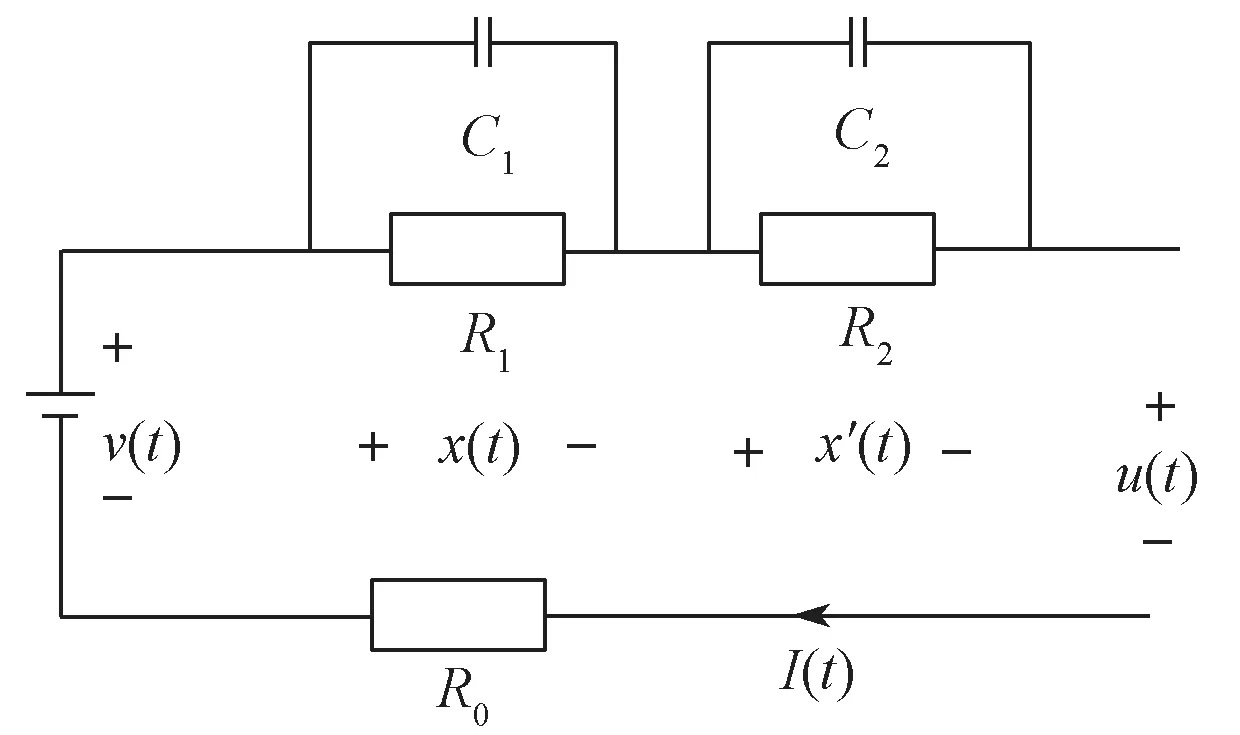
图3 二阶RC 等效电路模型Fig.3 Second-order RC equivalent circuit model

建立电池连续时间模型：

利用零阶保持器离散化并假设系统存在一阶纯滞后，得到离散时间模型：

用q-1表示一步平移算子，简化式（3）得到

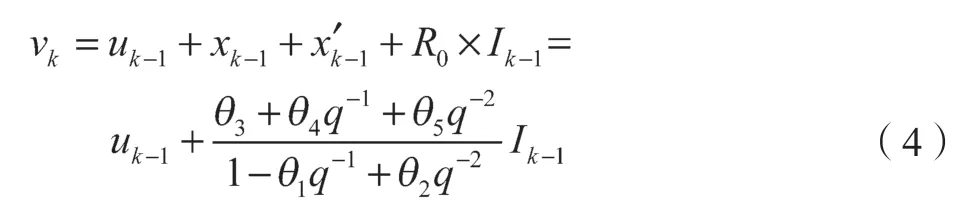
式中：θ1=α1+α2；θ2=α1α2；θ3=R0；θ4=R1+R2-R1α1-R2α2-R0α1-R0α2；θ5=(R0+R1+R2)α1α2-R1α2-R2α1。

假设扰动平稳且具有有理谱密度，扰动通道的极点多项式与过程通道相同，令zk=vk-uk-1，得到式（5）所示电池CARMA 模型：

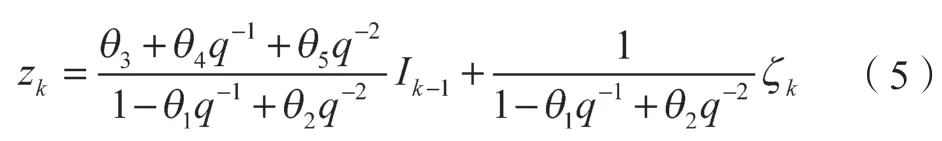
式中：{ξk}——同方差、独立（至少为不相关）、零均值的随机变量序列。

1.3 渐消记忆递推最小二乘法参数辨识

为解决传统递推最小二乘法的数据饱和问题，本文采用遗忘因子来减少旧数据所占权重，同时提高新数据比重；在每个采样间隔，基于当前的测量值更新参数估计值。渐消记忆递推最小二乘法具体实现过程如下：

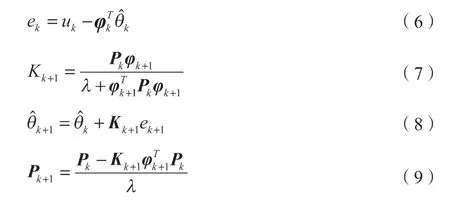
式中：k——时刻；φ——观测向量；——参数向量；e——模型残差；K——增益矩阵；P——误差的协方差矩阵；λ——遗忘因子，多取0.95 ≤λ≤1 ，λ越小，新数据在参数修正过程中所占权重越高，能更好地追踪参数变化，但同时受噪声影响大，参数估计波动较大。

实验过程中，由于采样周期足够小，电池放电能力有限，SOC 变化足够小，对应的开路电压变化很小，可以假设Δvk=vk-vk-1=0[11]，将其代入CARMA 模型，得到

辨识过程中取

式中：θ6k=(1-θ1k+θ2k)vk。

2 电池SOC 估计算法

要实现电池SOC 估计，首先应推导得到电池OCV 的最优估计表达式。基于式（5）所示电池CARMA 模型，结合广义预测控制相关知识，推导得到电池OCV 表达式[12]：

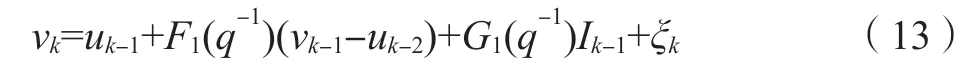
式中：G1(q-1)=θ3+θ4q-1+θ5q-2；F1(q-1)=θ1-θ2q-1。

以开路电压估计误差均值为零、方差最小为最优标准，推导电池OCV 最优估计表达式。用表示OCV 最优估计值，表示估计误差，具体过程如下[13]：

（1）OCV 误差均值为零

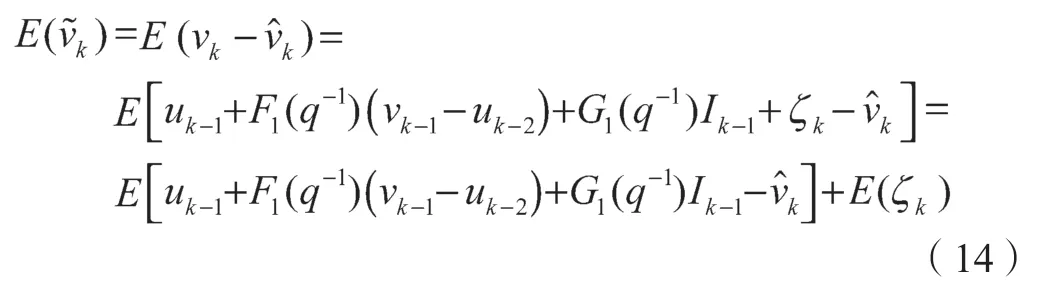
式 中，E(ζk)=0， 要 使， 当 且 仅 当，即。

（2）OCV 误差方差最小

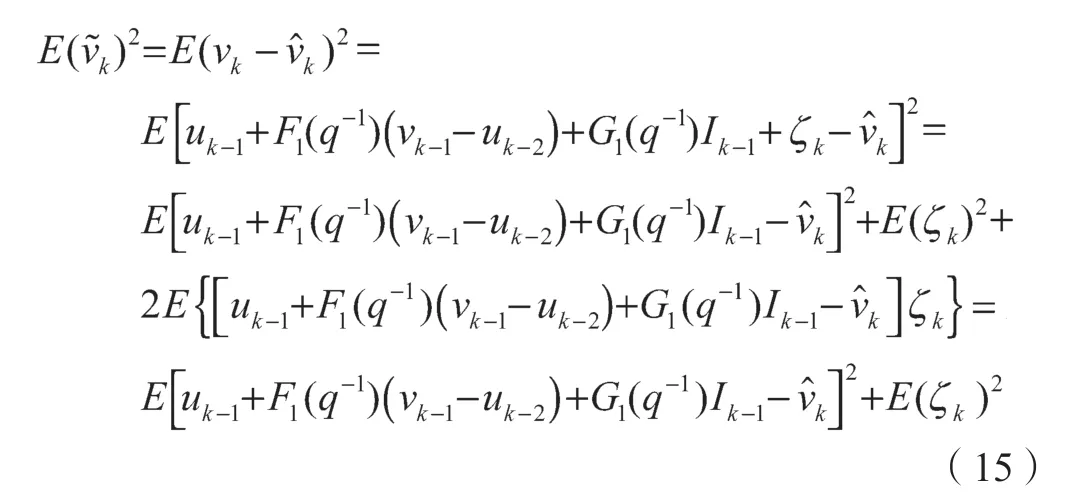
令E(ζk)2=σ2，当且仅当，即时，OCV 估计误差方差最小。此时，得到OCV 最优估计表达式为

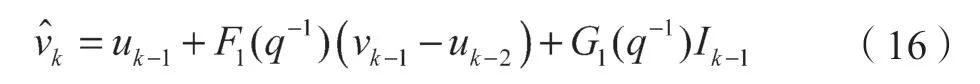
将实时辨识得到的k时刻各参数代入式（16），得到；结合建立的OCV-SOC 分段模型，计算出k时刻的SOC 值。重复该过程，递推得到下一时刻的SOC 值，实现基于CARMA 模型的SOC 估计。

3 试验与仿真

通过Matlab 仿真试验来验证本文提出的电池CARMA 模型及基于此模型的SOC 估计算法的准确性。

3.1 试验数据说明

本文仿真过程中使用数据来自马里兰大学先进寿命周期工程中心（center for advanced life cycle engineering，CALCE）电池公开数据集，选用圆柱形三元石墨锂电池INR 18650-20R 型电池单体试验数据：电池额定容量为2 000 mAh；充、放电截止电压分别为4.2 V和2.5 V；直径为18.33±0.77 mm，长度为64.85 ±0.15 mm；质量为45.0 g。本文主要选用25 ℃下美国联邦城市运行工况（The federal urban driving schedule，FUDS）[14]数据辨识电池CARMA 模型参数，并实现电池SOC 仿真估计。FUDS 作为城市驾驶车辆实际行驶工况的常用模拟，多年来一直被应用于电动汽车性能测试。FUDS 工况一个完整周期为1 372 s，相应的电流变化如图4 所示，整个实验过程中电池端电压、电流变化如图5 所示。

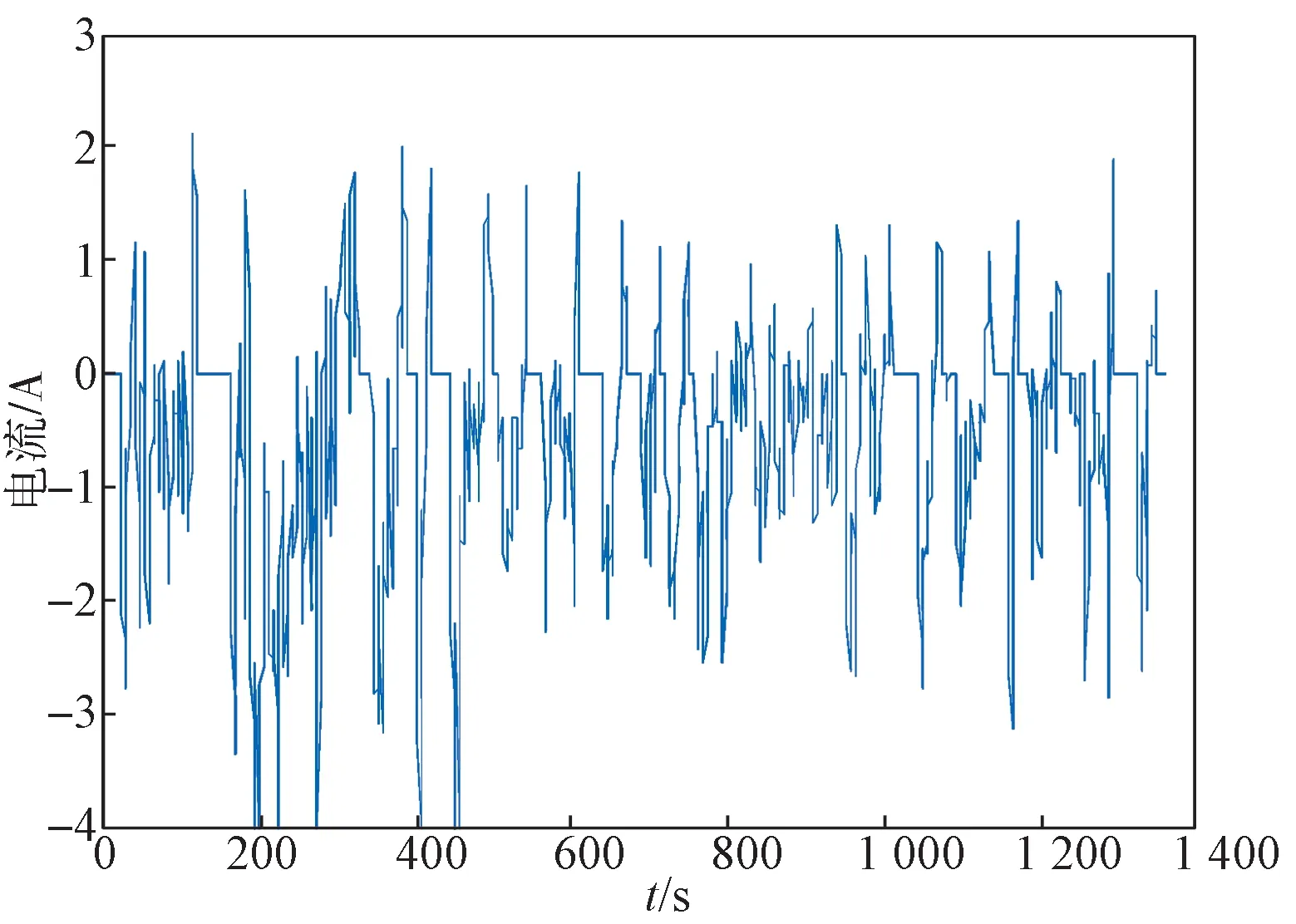
图4 FUDS 工况单周期电流变化Fig.4 Single-cycle current variation under the FUDS conditions

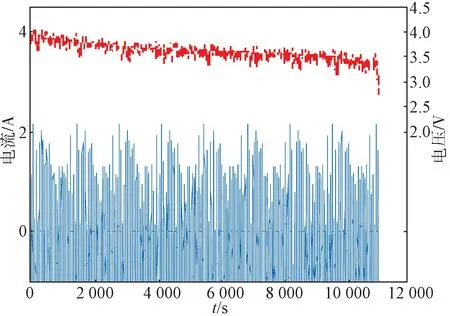
图5 FUDS 工况循环电压、电流变化Fig.5 Voltage and current variation under the FUDS conditions

3.2 CARMA 模型参数辨识及验证分析

用Matlab 实现电池参数辨识时，给定参数初始值λ=0.99，P(0)=105×I，I为6阶单位矩阵。按式（6）～式（9）进行辨识，得到FUDS 工况下各模型参数，具体如图6所示。

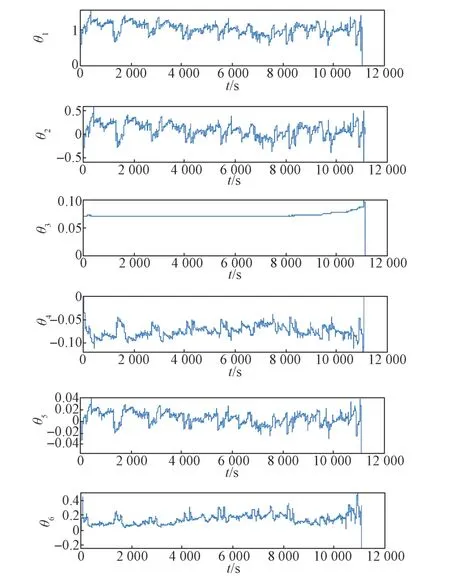
图6 CARMA 模型参数辨识结果Fig.6 Parameter identification results of the CARMA model

将辨识得到的参数代入式（17），估计电池端电压以验证模型准确性，得到模型输出端电压相比FUDS 工况下电池实际端电压误差，如图7 所示。

考虑到放电到最后时模型参数变化较为剧烈而导致辨识不准确，模型端电压误差曲线只给出前10 000个数据点，此时SOC 为6%。由图7 可以看出，端电压估计误差总体集中在±2 mV 之间，误差平均值为0.153 5 mV, RMSE 为0.594 8 mV，平均绝对误差（mean absolute error，MAE）为0.368 3 mV，与郑方丹等人研究得到的MAE 为0.291 mV 的结果所差无几[10]，较为准确地估计出电池端电压。因此所建立的电池CARMA模型可以被作为试验所用电池的等效模型。

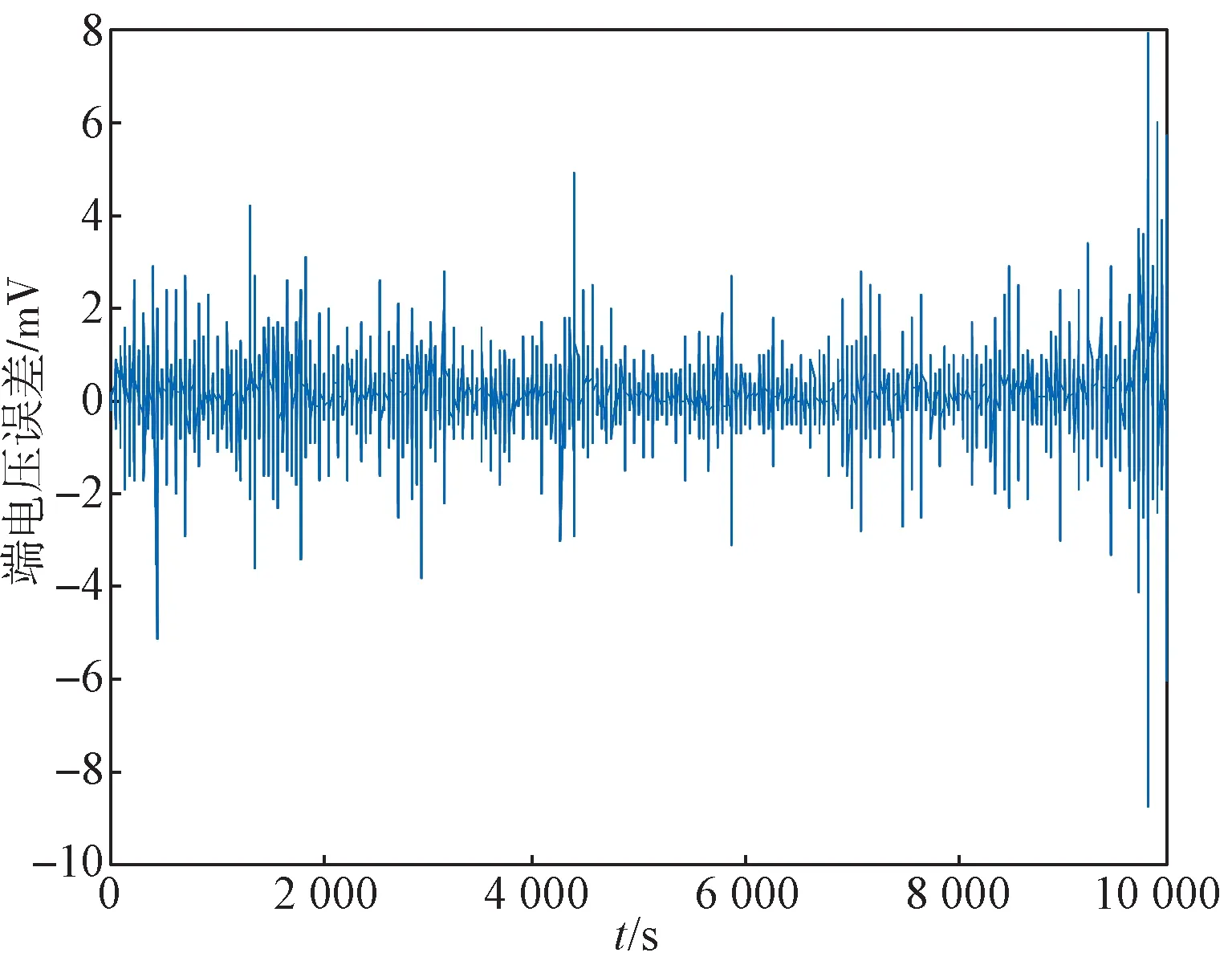
图7 CARMA 模型输出端电压误差Fig.7 Output voltage errors of the CARMA model

3.3 电池SOC 估计算法仿真验证

FUDS 工况循环试验过程中，SOC 初始值为0.8。考虑到SOC 值小于0.2 时，模型参数辨识不准确，会导致OCV 估计值存在较大误差，此时基于CARMA 模型的SOC 估计方法不再适用。为此，本文在SOC 值小于0.2 时，使用安时积分法继续估计电池SOC，得到FUDS 工况下SOC 估计值及误差如图8 所示。

图8 FUDS 工况下SOC 估计结果Fig.8 SOC estimation results under the FUDS conditions

分析SOC 估计结果可知，误差曲线的多个尖峰出现在电流值突变时，此时极化电阻剧烈变化，模型参数辨识不准确，造成较大的SOC 估计误差。SOC 估计的最大绝对误差为2.39%，误差平均值为-0.50%，RMSE为0.93%。可见，误差在可接受范围±5%之内。

4 结语

本文主要工作围绕电池建模及其SOC 估计展开，基于马里兰大学CALCE 三元石墨锂电池试验数据建立电池CARMA 模型，据此估计电池OCV，并结合OCVSOC 分段模型，实现电池参数的实时辨识以及电池SOC 的实时估计。

相较于简单的安时积分法，本文提出的基于CARMA 模型估计SOC 的算法准确度更高，且不会产生累积误差；相较于目前研究较多的卡尔曼滤波算法，本文提出的方法虽然在精确度上略有不足，但该法不涉及矩阵的大量迭代运算，运行速度更快，对计算能力要求较低，估计电池SOC 时不存在给定初值问题,适合汽车电池管理系统在线估计电池SOC；另外，与模型参数固定的常规卡尔曼滤波算法不同，采用本算法可实现模型参数在线实时辨识，对电池老化以及更换不同种类电池情况的适应性更好。

由于该SOC 估计算法中结合了开路电压法，在SOC-OCV曲线存在较为平缓平台时，该算法失效。此外，本文所用数据为25 ℃环境温度下试验得到，而实际电池性能受温度影响较大，后续可以就温度对电池SOC的影响做进一步研究。