基于感知区域覆盖的自动驾驶传感器布局优化方法

安 泰，刁望成

（兰州交通大学 机电技术研究所，甘肃 兰州 730070）

0 引言

自动驾驶是用传感器与计算机系统取代驾驶人员来处理车辆驾驶操作的技术[1]。环境感知是自动驾驶汽车的核心技术之一，其由多种车载传感器共同发挥效用。传感器作为自动驾驶汽车的环境感知元件，直接影响着计算机对感知信息的处理质量。车辆环境信息、车辆动态信息需要不同类型传感器来收集、整合，因此增强多类型传感器布局的合理性，对于提高环境信息数据的采集质量具有非常重要的现实意义。

国内外大量学者围绕传感器布局优化问题进行了大量的研究：朱炜昱等人通过分析不同传感器的工作特性和限定条件，总结了传感器在布局时的注意事项[2]；王俊在分析自动驾驶车辆感知技术实现方法的基础上设计并实现了一种激光传感器及视觉传感器的自标定和联合标定方法[3]；Shenyu Mou 等人提出了一种传感器空间优化方法，即通过对传感器覆盖范围进行分割，将最优配置转化为非线性优化问题进行求解[4]；高飞应用空间几何理论，面向视觉传感器的感知特性建立了视觉传感器的三维几何模型[5]；Farsam Farzadpour在传感器感知区域的研究中提出了“视锥”的概念，并在此基础上建立了传感器的感知模型[6]；张昊等人研究了基于雷达点云数据生成数字表面模型（digital surface model, DSM）的方法，为运用DSM 技术建立感知对象模型奠定了理论基础[7]；张双喜对传感器、感知对象不同坐标系之间的转换问题进行了深入研究，为优化传感器系统布局提供了基础条件[8]；张品等人针对传感器网络的覆盖问题提出一种基于权值的优化覆盖算法，使无线传感器网络布局得到优化[9]；俞佳莹提出了一种超声波传感器感知模型，解决了侧向目标的超声波传感器感知效果优化问题[10]；Farsam Farzadpour 等通过分析相机安装参数与覆盖性能的关系，提出了一种面向宽域感知的相机参数选取方法[11]；李子杰等人建立了栅格加权侦察覆盖指数，对预指定的侦查区域赋以权重划分，解决了侦察航路优化的问题[12]；郑亮等人基于PSO 算法建立风电系统仿真模型，对系统中的参数进行了自整定[13]。上述研究成果在传感器建模、感知对象建模和单一类型传感器安装位置优化等方面分别进行了研究，但是关于如何解决自动驾驶传感器的合理布局问题的研究成果较少，尚需进一步深入研究。

为此，本文针对如何量化评价多类型传感器综合感知性能、如何刻画感知对象复杂曲面特征、如何判定感知对象覆盖范围以及覆盖范围内复杂曲面面积计算等问题进行了研究，提出了一种自动驾驶车辆多类型传感器优化布局方案，并通过计算机仿真验证了该布局优化方案的有效性。

1 传感器及感知环境建模

1.1 传感器建模

为构建合理的自动驾驶汽车传感器布局，首先运用计算几何理论对车载传感器的视域空间进行几何建模。本文以激光雷达、毫米波雷达和视觉传感器这3 类传感器作为研究对象。其中，激光雷达传感器为多线激光雷达，其多被安装在车顶，可全方位扫描感知范围内的障碍物；毫米波雷达多被安装于车辆前端，其作用是捕捉动态的目标信息，毫米波雷达在雨雪环境中比激光雷达具有更好的感知效果；视觉传感器可以获取环境的图像信息，并且可以由采集到的图像信息经计算机算法识别感知对象[2]。

激光雷达是通过向目标发射激光光束并分析其反射光束来完成感知的，探测范围由其俯仰角和旋转角决定，由此构成了垂直方向锥形立体感知区域。毫米波雷达是通过在短时间内发送大功率的脉冲信号并同时对回波信号进行放大处理来完成感知功能的，其水平视场角和垂直视场角均比激光雷达的小，构成检测距离更远但张角略小的锥形立体感知区域。视觉传感器可以通过镜头汇聚外界光线，并通过调整焦距使光线落在镜头后面传感器的平面上，同理，其视域也由张角略宽的椎体构成。

3 类传感器视域特征及参数如表1 所示，三者都是通过定点发出/接收光线完成感知过程，其光束组合都在空间中形成椎体。

表1 自动驾驶汽车常用传感器视域参数表Tab.1 Field parameters of sensors commonly used in autonomous vehicle

基于感知原理上的相似性，可以对3 类传感器的感知视域属性进行归一化建模。故面向传感器的感知区域属性可抽象为用六元组表示，具体模型如式（1）所示。其中P是传感器安装位置，用三维坐标(x,y,h)表示；向量表示该传感器主感知方向，传感器安装角度由俯仰角γ和水平旋转角θ确定；传感器的感知区域由垂直视场角2β和水平视场角2α确定；传感器的有效感知距离由最远感知距离R和最近感知距离r确定。

传感器的感知区域可抽象为一个三维棱台，如图1所示。

图1 传感器视域的几何建模Fig.1 Geometric modeling of sensor view field

1.2 感知对象建模

DSM 模型是在数字高程模型（digital elevation model, DEM）的基础上增加了感知对象高度和距离信息的模型，其基于地理信息对地表物体高度值进行模拟。在自动驾驶领域的感知对象建立中，可将车辆、行人的外形空间抽象成垂直于地面的体元素组合，应用DSM技术快速构建感知对象模型。本文采用距离加权平均插值法进行建模，具体步骤如下：

（1）对离散的点云数据建立规则格网（Grid）模型。格网尺寸大小一般由被感知对象大小确定，根据自动驾驶领域常见感知对象体积，本文拟采用的三维格网尺寸为2 cm×2 cm×2 cm。

（2）选取插值半径，确定内插点所在的格网单元，并选取适当邻域。感知对象模型精度与插值半径直接相关，最佳的插值半径与点云数据的平均间距相近[14]，本文选取的插值半径为1.8 cm。

（3）采用距离加权平均插值法计算内插点的高度值，具体如式（2）所示。

式中：ZA——感知对象上的任意插值点A 的垂直高度值（DSM 值）；Zi——感知对象上与插值点A 相邻的各采样点的DSM 值；di——格网尺寸。

基于感知对象的DSM 模型建立过程，感知对象外形空间特征可由如下六元组进行描述：

式中：xA,yA——A点水平坐标系中的横向与纵向坐标；I——感知对象中斜线的坡度，I=h/l×100%，其中h和l分别为以该斜线构成的直角三角形的高度和长度；K——感知对象中曲线上点的曲率，，其中Δα为某段曲线的切线转角，Δs为该段曲线的弧长。

感知对象的DSM 模型如图2 所示，通过对激光雷达点云数据的处理，生成车体初步的三维模型；再通过三维格网建立感知对象的DSM 模型。

图2 点云数据到DSM 模型的转换Fig.2 Transformation from point cloud data to DSM model

2 基于感知覆盖范围的传感器布局优化设计

2.1 传感器感知区域加权覆盖面积的定义

加权覆盖面积S0表示传感器在自动驾驶汽车行驶中对感知对象的覆盖能力。加权覆盖面积越大，说明传感器探测到的感知对象信息越全面。本文将以加权覆盖面积S0作为传感器布局评价指标，其大小由式（4）表示。

式中：S1——传感器视域与感知对象相交的表面积，即感知覆盖面积；ω——覆盖面积S1的权值，用来描述感知对象所处位置对自动驾驶安全行驶的威胁程度，距离越近，权值越大，具体计算如式（5）所示。

式中：C——常数；x——感知对象位置坐标与传感器安装位置坐标的距离。

2.2 基于DSM 模型的离散化处理

为了计算加权覆盖面积，本文引入离散化思想，通过全等的三角形格网对DSM 模型表面进行离散化，将其表面面积转化为三角形格网面积（图3）。

图3 DSM 模型离散化处理图Fig.3 Discrete processing diagram of DSM model

进行离散化处理之后，三角形格网中的每个离散化单元由三角形的中心点表示，离散化单元感知判定等价于三角形中心点的感知判定。DSM 模型经离散化后，感知对象加权覆盖面积的计算如式（6）所示。

式中：Si——离散化单元面积；ωi——离散化单元的权重。

2.3 基于离散化方法的传感器布局优化模型

本文以激光雷达、毫米波雷达和视觉传感器这3 类传感器构成的环境感知系统为例，以传感器感知区域加权覆盖面积为目标函数，传感器的安装位置和安装角度为决策变量，构建基于感知对象离散化的传感器布局优化数学模型。模型中，感知对象加权覆盖面积计算通过离散化单元判定进行累加，离散化单元是否被感知可借助三角形格网中心点是否被感知进行判断。

感知对象的DSM 模型经离散化为三角形格网后，则将感知对象加权覆盖面积计算问题转化为离散化单元加权覆盖面积的累加计算问题。将每个离散化单元由三角形中心点表示，问题进一步转化为三角形中心点权值的确定和中心点是否在传感器感知区域内的判定问题。三角形中心点权值是根据中心点与传感器安装位置的距离计算确定，见式（5），三角形中心点被感知的判定方法示意如图4 所示。

图4 离散化单元中心点感知判定Fig.4 Perception judgment of discrete element center point

经过被感知对象表面任意离散单元的中心点M(xi,yi,hi)作矩形D1D2D3D4中直线L的平行线L′，以P点和L′线构成辅助平面ψ，其中L与矩形D1D2D3D4中D3D4线平行。传感器主感知方向向量在辅助平面ψ上的投影记作′，′与矩形D1D2D3D4的交点记为P″，点P″在辅助平面ψ上的投影点记为F点，PF与PM的夹角记为αi，通过比较αi与角α的大小判断M点是否在传感器的水平感知区域内（图4(a)）。同理，过点M(xi,yi,hi)作矩形D1D2D3D4中直线K的平行线K′，以P点和K′线构成辅助平面Ω，其中K与矩形D1D2D3D4中D1D3线平行。传感器主感知方向向量在辅助平面Ω上的投影记作″，点P″在辅助平面Ω上的投影点记为E点，PE和PM的夹角记为βi，则通过比较βi与角β的大小可以判断M点是否在传感器的垂直感知区域内（图4(b)）。除了判断离散化单元中心点是否在传感器感知视场，还需要判断离散化单元中心点是否在传感器的感知距离范围内。为此，本文根据实际感知需求设定了最近感知距离r和最远感知距离R。综上所述，离散化单元是否被感知的判定条件为式（7）～式（9）。

为了建模方便，定义辅助变量Tij。Tij取1，表示索引为i的离散化单元在索引为j的传感器感知范围内；否则，Tij取0。传感器布局优化模型为

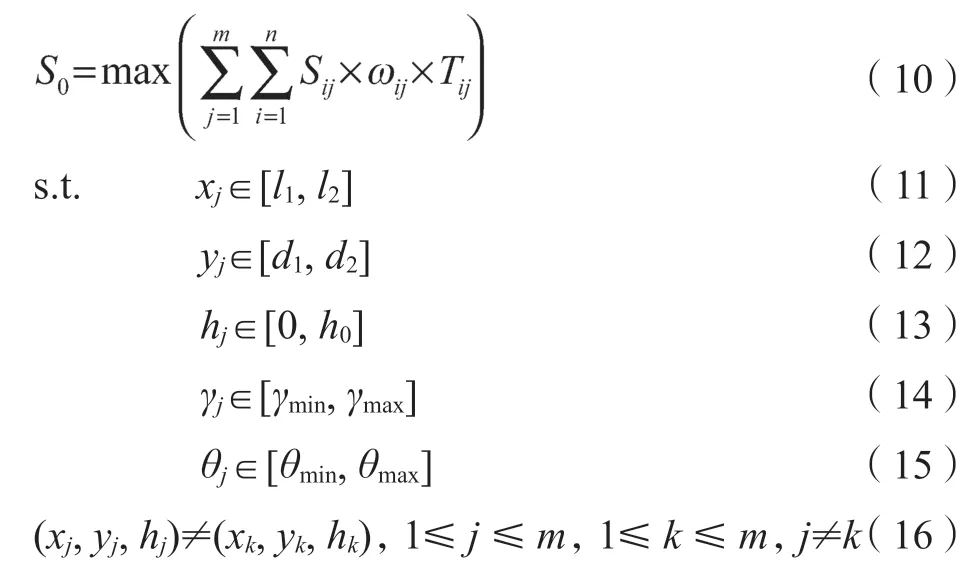
模型中式（10）是目标函数，表示多个传感器对感知对象的加权覆盖面积之和，其中j为传感器索引，m为传感器数量，i为感知对象离散化单元索引，n为离散化单元数量；式（11）～式（13）表示每个传感器可行的安装位置范围，其中，xj，yj，hj分别为传感器安装位置的横坐标、水平长度坐标和高度坐标；式（14）～式（15）表示每个传感器可行的安装角度范围；式（16）限定各个传感器不能安装在同一个位置。

3 优化算法设计

本文提出的传感器布局优化模型的求解需统筹考虑多个传感器的安装位置和安装角度，并以多个传感器的加权覆盖面积最大化为优化目标，通过在安装位置和安装角度的可行域中搜索，获取最佳的传感器安装位置和安装角度。模型的求解需确定多个传感器的多个外部参数，以实现整个感知系统感知性能的优化，该模型属于典型的组合优化问题。

粒子群优化算法(particle swarm optimization ，PSO)属于进化算法的一种，是求解组合优化问题常用的随机搜索算法。PSO 中优化问题的潜在解都被视为一枚“粒子”，本文中的“粒子群”即为某种传感器的安装位置和安装角度的集合。传感器安装的3 个位置参数以及2 个角度参数的优化结果可以用粒子的迭代位置值xid表示，而粒子的迭代速度vid则代表着寻优过程中参数迭代的增量，粒子主要通过迭代的方式追寻个体极值和全局极值，最终得到安装位置参数及角度参数的最优解。算法中粒子的迭代公式如下：

本文设计的粒子群算法参数设置如表2 所示。

表2 粒子群算法参数表Tab.2 Parameters of the PSO algorithm

算法中，适应度函数计算过程被嵌入了基于感知对象离散化的加权覆盖面积计算方法，算法首先完成传感器感知模型的内部参数、外部参数、感知对象离散化模型数据以及距离的初始化，并进行坐标转化；然后进行基于传感器和感知对象离散化单元的内、外二重循环。内循环是基于感知对象离散化单元个数的循环，遍历感知对象全部离散化单元，并对每个离散化单元进行感知判定，累加被当前传感器覆盖的表面积；外循环是对每个传感器进行循环，将每个传感器覆盖感知对象的面积进行累加，得到全部传感器的覆盖面积和，即目标函数值。内循环依据2.3 节中提出的判定方法进行判断，实现每个传感器对离散化单元的感知判定和加权覆盖面积的计算。该方法具体流程如图5 所示。

图5 粒子群算法流程Fig.5 Flow chart of the PSO algorithm

4 仿真验证

为验证本文所建立的传感器布局优化模型的正确性及粒子群算法对模型求解的有效性，模拟实际自动驾驶场景进行仿真实验，其中自动驾驶车辆高度为3.2 m，宽度为2.65 m；感知对象距离为50 m。仿真实验运行操作系统为Microsoft Windows 7，仿真工具为Matlab 2014R，计算机配置为处理器Intel(R)Core(TM)i5@2.5GHz,内存4.00 GB。优化算法中场景初始参数设置如表3 所示。

表3 优化场景参数设置Tab.3 Optimize scenario parameter settings

基于上述模拟仿真实验参数设置，通过粒子群优化算法对传感器布局优化模型进行了模拟实验仿真，传感器布局优化评价指标随迭代次数收敛的曲线如图6 所示。由图6 可以看出，随着传感器安装位置和安装角度迭代，传感器的覆盖面积之和不断增加，加权总覆盖面积的平均值在第80 代左右达到最大值并趋于稳定，传感器覆盖面积的增加是由于传感器的安装角度和安装位置发生改变，通过调整传感器的安装位置和安装角度能够实现多传感器覆盖面积之和的增加，采用本文提出的方法可以获得最优的加权覆盖面积，同时可以得到对应传感器的安装位置和安装角度。

图6 加权总覆盖面积迭代图Fig.6 Iteration chart of weighted total coverage area

传感器的安装位置和安装角度收敛曲线如图7 所示，其中图7（a）是传感器水平安装角度θ的优化迭代曲线，图中3 种传感器均经过90 代左右稳定于1.600 rad。图7（b）是3 种传感器的垂直安装角度（即俯仰角）γ的优化迭代曲线，图中激光雷达的俯仰角经约70 代稳定在1.600 rad，而毫米波雷达和视觉传感器的安装俯仰角均在90 代左右稳定趋于1.200 rad。图7（c）是传感器安装位置的X坐标收敛曲线，3 个传感器的X坐标均在给定区域内搜索最优解，最终收敛于300 mm 左右。图7（d）是传感器安装位置的Y坐标收敛曲线，由于毫米波雷达和视觉传感器Y坐标位置是固定的，因此只有激光雷达的Y坐标收敛曲线，激光雷达在迭代50 代之后收敛于1 500 mm 左右。图7（e）是传感器安装位置的H坐标收敛曲线，由于激光雷达H坐标确定，因此只有毫米波雷达和视觉传感器H坐标收敛曲线，毫米波雷达在15 代左右收敛于1 400 mm，视觉传感器则在20 代时收敛到800 mm。

图7 传感器的安装位置和安装角度收敛曲线Fig.7 Convergence curves of sensor installation position and angle

由图7 中5 个传感器布局优化评价指标的收敛曲线总体来看，粒子群算法在80 代左右即可收敛，进而得到各个传感器优化之后的安装位置和安装角度。由图7（c）～图7（e）传感器外部参数的收敛曲线可以看出，传感器的安装位置在给定的约束条件范围内进行寻优，在算法收敛后得到较好的传感器外部参数。通过上述仿真实验，验证了以传感器加权覆盖面积为评价指标、基于DSM 技术和离散化思想的布局优化方法的有效性。

为了进一步定性分析传感器的安装位置和安装角度对加权覆盖面积的影响关系，确定传感器外部参数对感知系统感知效果影响的权重，分别在确定的传感器安装位置和传感器安装角度条件下进行仿真实验，仿真结果如图8 所示。其中图8（a）～图8（c）是在传感器安装角度确定、安装位置不确定情况下的安装位置坐标与加权覆盖面积的关系图，每个图中的纵轴均为加权覆盖面积，水平方向的两个坐标轴的是由安装位置中变化的维度确定。图8（d）～图8（f）是在安装位置确定的情况下，安装位置的水平安装角度、垂直安装角度与加权覆盖面积的关系图。

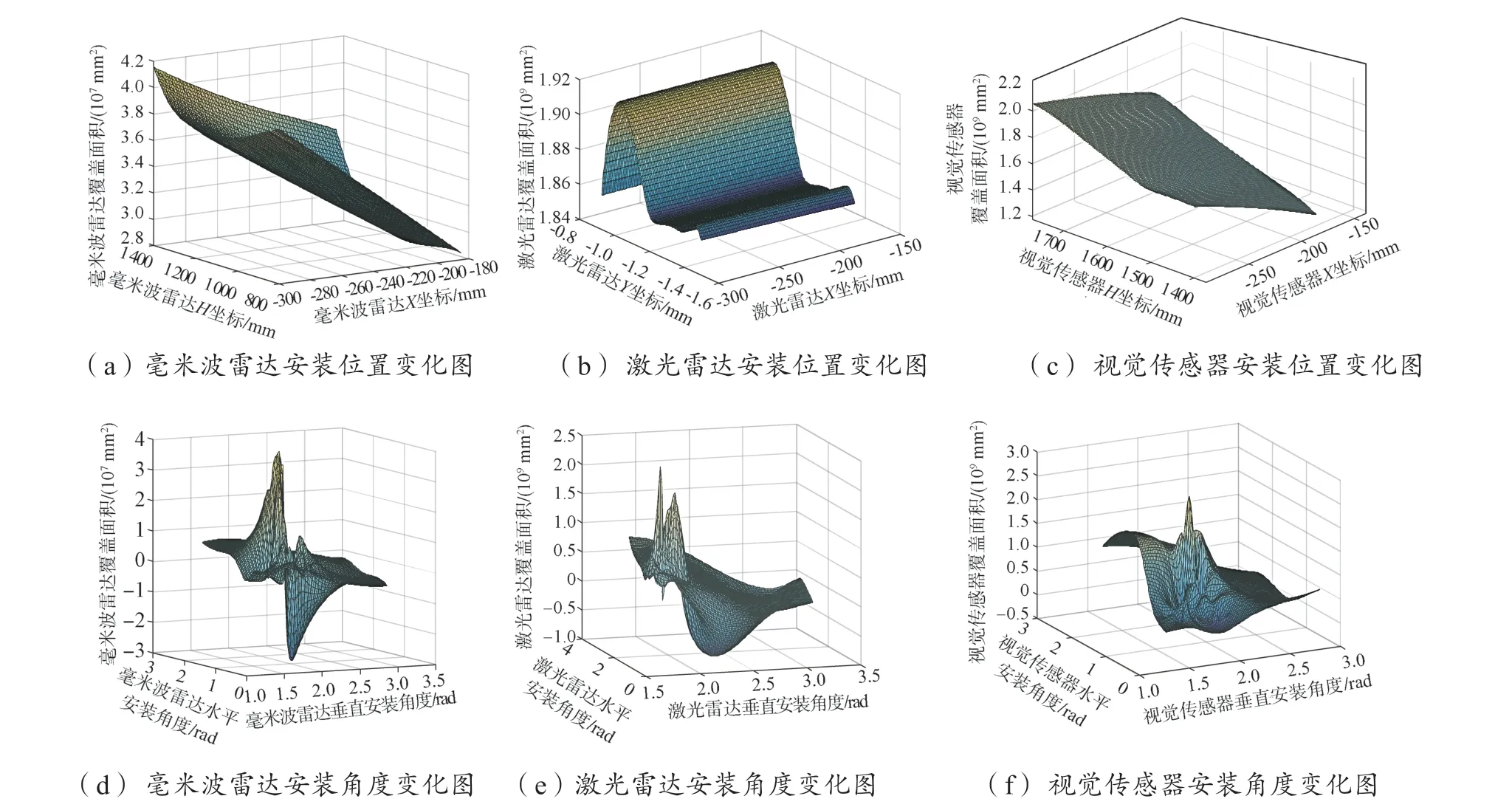
图8 传感器外部参数对加权覆盖面积影响对比Fig.8 Comparison of influences of external parameters on weighted coverage area

由图8（a）～图8（c）可以看出，以两位置坐标变量为坐标轴的三维图像呈平滑的曲面状，说明两位置坐标变量的变化比较整齐，传感器覆盖面积数值没有剧烈的变化。由图8（d）～图8（f）中可以看出，三维图像呈不平整曲面状并有峰值的出现，变化的起伏程度也十分明显，说明传感器覆盖面积随着安装角度参数的变化变化比较剧烈。由上述分析可知，在安装位置确定的情况下，传感器的安装角度对布局评价指标的影响较大，传感器的安装位置对布局评价指标的影响较小，尤其是激光雷达，如图8（b）所示，激光雷达的加权覆盖面积随着X坐标变化基本没有变化，这是由于激光雷达是360°的感知视场，其水平安装位置对加权覆盖面积没有影响。综上所述，传感器的外部参数当中安装角度对感知效果的影响较大，是相对重要的影响因素。

5 结语

针对基于感知对象加权覆盖面积的传感器布局，本文提出的优化方法具有以下特点：

（1）在传感器感知区域归一化分析的基础上，引入空间几何理论并建立了基于空间棱锥的传感器六元组几何模型，有效降低了多类型传感器综合感知模型的复杂性。

（2）采用地理信息技术建立感知对象的DSM 模型，方便、准确地刻画了感知对象复杂曲面的外形特征。

（3）设计了基于离散化思想的感知对象加权覆盖面积计算方法，建立了基于感知对象加权覆盖面积的布局评价指标及布局优化模型，并采用粒子群算法对模型进行求解，进而得到了一种优化自动驾驶汽车传感器布局的一般性解决方案。

仿真实验结果表明，采用该方法可以获取感知效果较好的传感器安装位置和安装角度，为自动驾驶车辆感知系统布局提供科学的决策依据。后续将围绕基于传感器优化布局的自动驾驶汽车在特定交通场景下开展复杂障碍物的感知研究工作，具体涉及3 个方面：（1）在具体特定的交通场景中，自动驾驶车辆的传感器布局的可靠性和安全性分析与测试；（2）在高速/低速的运行条件下，自动驾驶车辆的传感器布局有效性的对比分析；（3）在多障碍物或移动障碍物的情景下，自动驾驶车辆的传感器布局的障碍物检测有效性分析。