双层结构模型预测控制稳态优化层QP 与LP 求解模态分析

王洪瑞 ，张 鑫 ，刘博文 ，蔺 娜，邹 涛

（1.中国科学院 网络化控制系统重点实验室，辽宁 沈阳 110016；2.中国科学院 沈阳自动化研究所，辽宁 沈阳 110016；3.中国科学院 机器人与智能制造创新研究院，辽宁 沈阳 110169；4.中国科学院大学，北京 100049；5.国家科技风险开发事业中心，北京 100038；6.广州大学，广东 广州 510006）

0 引言

模型预测控制算法（model predictive control ，MPC）能有效地处理约束、多变量、耦合和纯滞后问题，已经在流程工业中得到了广泛应用[1-3]，在学术上也得到了深入的研究[4-8]，但理论研究与工程应用的衔接不够紧密，不能很好地相互促进。本文将研究其中两方面的问题：一是软件开发尚存在标准化及计算机求解方面的问题，由于MPC 软件价格昂贵，很多企业难以接受，因此企业或面向工程的研究人员自主开发MPC软件的需求较大，而软件开发要求MPC 具有通用、标准化、能够利用计算机求解的描述，从当前公开的理论研究成果来看尚无这方面内容；二是工程应用中如何配置MPC 的参数问题，很多先进过程控制（advanced process control，APC）工程师采用试错法调试参数，效果差、效率低，例如商业软件都提供线性规划(linear programming, LP)和二次规划(quadratic programming,QP)两种求解选项，但在选择求解方法以及各方法对控制性能的影响分析方面没有很好的理论指导。

目前工业应用中主流MPC 采用集成稳态优化与动态控制的双层结构MPC，它在常规MPC 动态控制层之上增加稳态优化层，可计算存在过程约束时可行的动态控制层的设定值[9-12]。为保证工业过程中每个优化控制周期内MPC 都能给出合理的优化值，稳态优化层采用两阶段法：第一阶段进行可行解判定及软约束调整，保证存在可行空间；第二阶段在可行空间内进行经济优化。稳态优化的两个阶段最终都可转化为一系列LP 或QP 问题，进而利用成熟的LP 或QP 求解算法进行求解。

本文基于MPC 已有研究成果及工程应用中存在的问题，研究双层MPC 稳态优化问题转化为LP 或QP 问题的标准化流程[13]，并进一步分析稳态优化LP 与QP解的空间特性[14]，给出LP 与QP 选择依据，为双层MPC 的软件开发及工程应用提供理论支撑。

1 两阶段稳态优化算法标准化

稳态优化算法中的每个阶段都是求解有约束数学规划问题，即在满足约束条件的前提下最小化目标函数。按照在优化过程中的满足情况，其约束条件可分为硬约束（必须满足）和基于优先级的软约束（可以不满足，按照优先级进行放松）[15-17]。为了提高计算效率，一般根据操作变量（manipulated variable，MV）与被控变量（controlled variable，CV）间的关系将控制器分为几个独立的子控制器，各个子控制器间的CV 不存在耦合关系。本节研究基于优先级的两阶段稳态优化算法的标准化过程，研究对象为子控制器。

1.1 约束条件标准化

通过对边界条件加极小值解决数值截断误差造成的优化不可行问题，对原始约束条件进行标准化描述，并基于优先级对其进行排序。

1.1.1 约束条件原始形式

设被控对象MV 个数为m，CV 个数为n。CV 分为稳定型与积分型两种类型，设稳定型CV 个数为ns，积分型CV 个数为nr，则ns+nr=n。

（1）硬约束

MV 上下限约束：

MV 增量约束：

（2）软约束

MV 设定值约束：

稳定型CV 上下限约束：

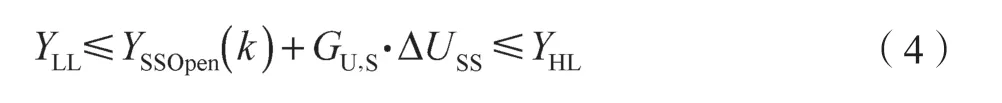
稳定型CV 增量约束：

稳定型CV 设定值约束：

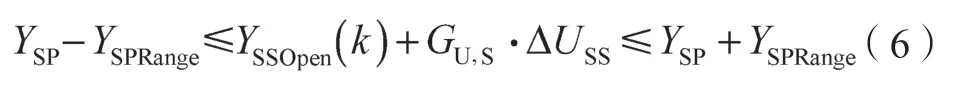
积分型CV 斜率控制范围：

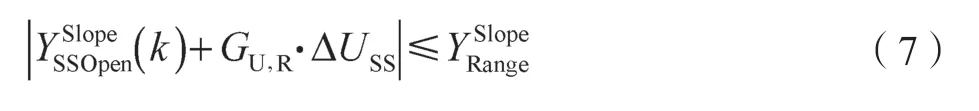
积分型CV 斜率安全范围：

式中：ULL——MV 操作下限，m维向量；UHL——MV操作上限，m维向量；+ΔUSS——MV 稳态增量，m维向量；U(k)——MV 当前值，m维向量；ΔUmax——MV最大增量，m维向量；USP——MV 设定值，m维向量；USPRange——MV 设定值范围，m维向量；YLL——CV 操作下限，ns维向量；YHL——CV 操作上限，ns维向量；YSSOpen(k)——CV 开环稳态值，ns维向量；GU,S——稳定型CV 增益矩阵，ns×m维矩阵；GU,R——积分型CV 斜率矩阵，nr×m维矩阵；ΔYmax——CV最大增量，ns维向量；YSP——CV 设定值，ns维向量；YSPRange——CV 设定值范围，ns维向量；——积分型CV 开环稳态斜率，nr维向量；——积分型CV 斜率控制精度，nr维向量；——积分型CV 斜率安全范围，nr维向量。

1.1.2 约束条件标准形式

MPC 一般采用内点算法（IPOPT）求解[18-20]，需将约束条件转化为A×ΔUSS≤B的标准形式。其中：

式（9）中的软约束并不是都存在的，某个MV 或CV 的设定值约束是否存在由设定值开关决定，至于是稳定型CV 约束还是积分型CV 约束，则由相应的CV类型决定。

1.1.3 基于优先级的约束排序

硬约束个数为2m，软约束的个数设为Nc，约束矩阵A及约束边界B按照硬约束及软约束分块表示为

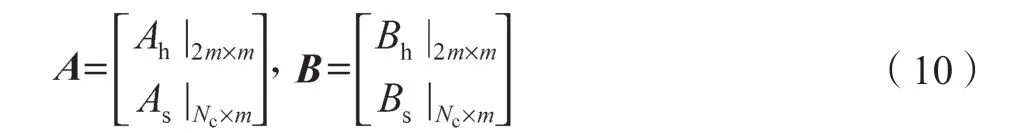
式中：下标h 代表硬约束边界；s 代表软约束边界。

每个软约束设置优先级R和放松权重W，分别表示为列向量：

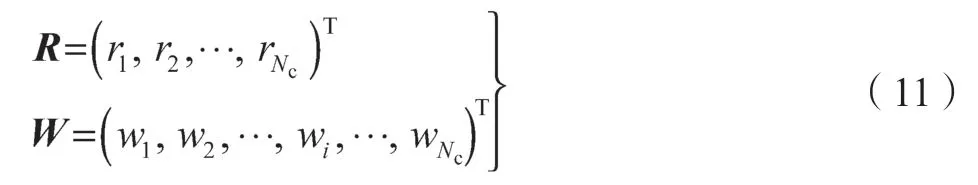
设共有Nr个不同的优先级，从高到低排列，各个优先级的约束个数排列成列向量NR：

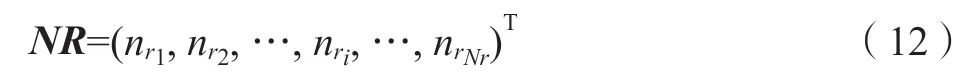
按照优先级从高到低将软约束进行重新排序，得到新的约束矩阵、约束边界、优先级向量、权重向量：

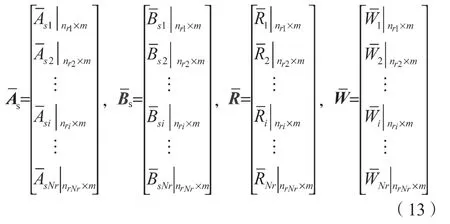
1.2 基于优先级的软约束松弛

设松弛变量为列向量ε，按照不同优先级表示为分块向量：

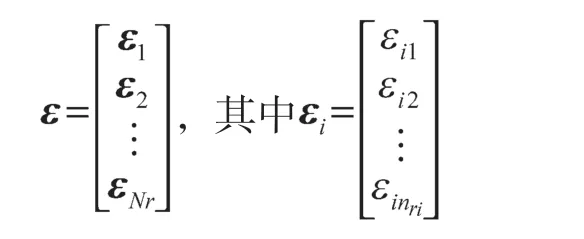
按照优先级进行约束松弛，每个优先级松弛问题形成一个LP 或QP 问题，依次进行求解；每个优先级的松弛变量值在下一个优先级的求解中被固定，将高优先级软约束作为低优先级松弛问题中的硬约束。

由于采用计算机求解，数值求解过程存在截断误差，则高优先级松弛变量固化后由于截断误差可能造成低优先级松弛问题不可行。为避免此问题，提出在构造低优先级松弛问题时，将上一优先级的松弛变量加上一个极小值δ（δ与ε同维，且分块方式相同），该值可等于设定的数值求解精度。求解过程描述如下：

（1）优先级最高的约束松弛问题

目标函数：

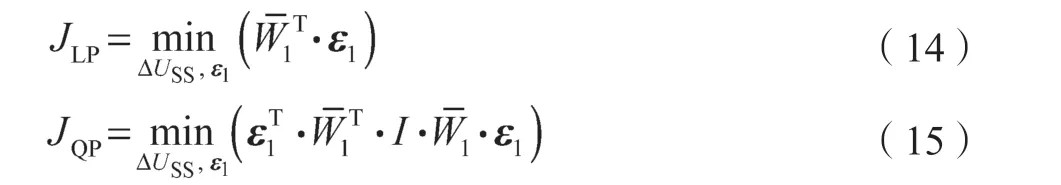
约束条件：

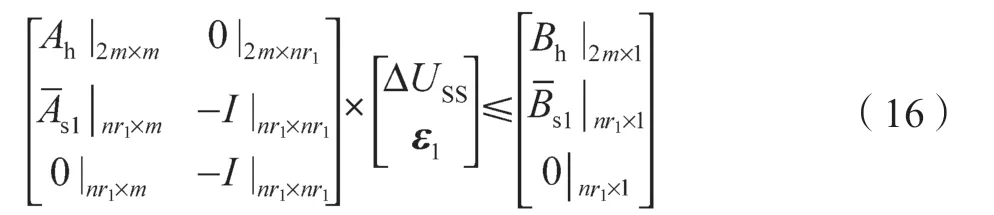
其中，JLP表示线性型目标函数，JQP表示二次型目标函数，下文定义与此一致。

（2）优先级为i(i=1, 2, …,Nr)的约束松弛问题

目标函数：

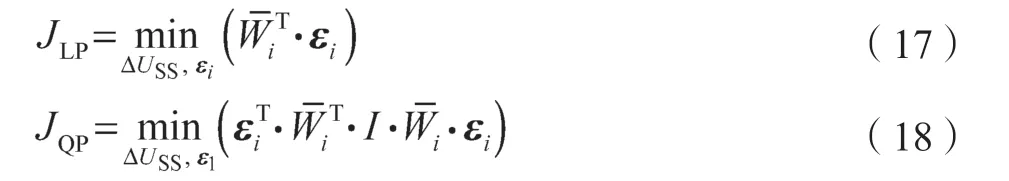
约束条件：

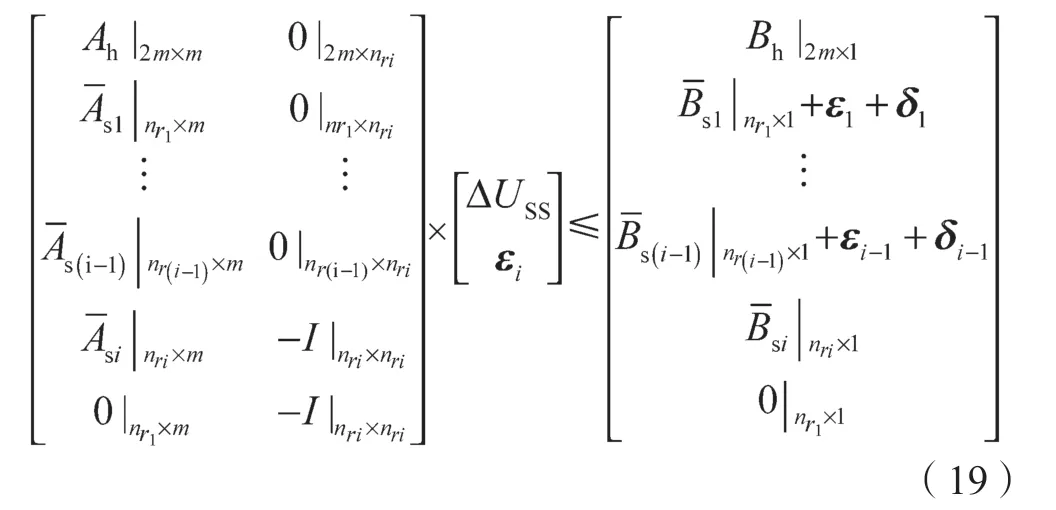
1.3 经济优化

软约束松弛结束后可进一步执行经济优化，决策变量为各个MV 的增量，可分为代价变量和最小移动变量两种类型。设代价变量为v个，则最小移动变量为(m-v)个，排列前面v个为代价变量，后面的为最小移动变量。优化问题由目标函数及约束条件两部分描述，下面分别从这两方面对LP 及QP 经济优化问题进行阐述。

（1）原始形式

LP 经济优化目标函数：

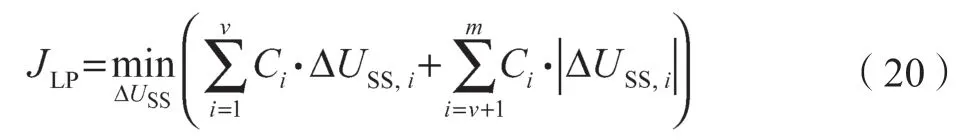
QP 经济优化目标函数：

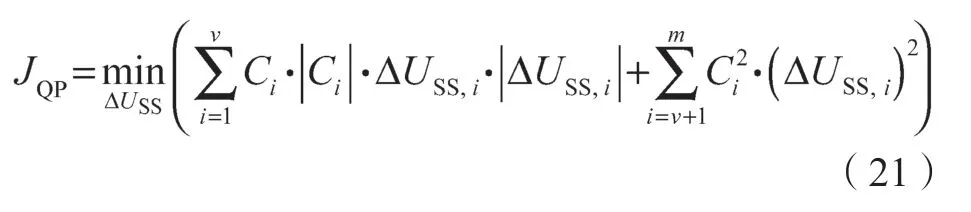
LP 及QP 约束条件相同：

（2）标准形式

由于原始描述目标函数中含有决策变量绝对值形式，不利于优化问题的求解，因此针对每个绝对值项引入两个辅助变量及相应约束条件[21]：

则经济优化标准化描述如式（24）～式（27）所示，其中表示形式为Ah,(v+1)～m的矩阵表示Ah的第(v+1)列至m列。

（a）LP 经济优化标准化

目标函数：

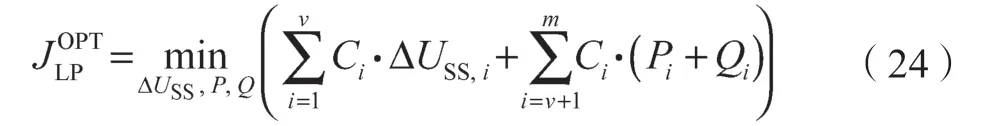
约束条件：

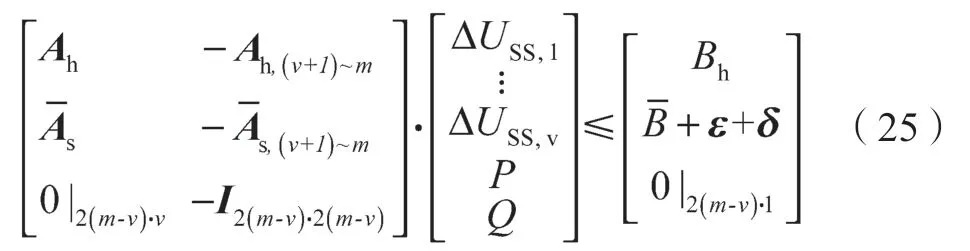
（b）QP 经济优化标准化

目标函数：

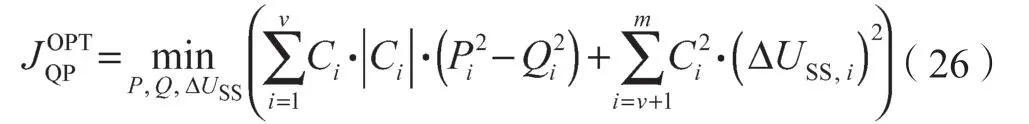
约束条件：

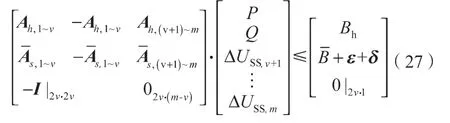
2 LP 与QP 解特性分析

根据上述分析可知，在稳态优化的软约束调整阶段及经济优化阶段，目标函数可以采用线性函数或者二次函数，从而分别构成约束条件相同的LP 及QP 问题；本节将通过研究LP 及QP 解的特性来解释提供这两种稳态优化描述形式的原因并给出这两种形式的选择依据。

2.1 几何关系分析

一般约束条件为凸集。LP 问题是平移一个截距可变的超平面（二维退化为直线）与约束空间相交于一点，并使得超平面的截距最小，其交点一定为约束空间的顶点；QP 问题是扩张一个半径可变的超椭球（二维退化为椭圆）与约束空间交于一点，并使得超椭球的半径最小，交点在约束空间边界平面上或某个固定点。随着目标函数权重变化，线性规划最优解在约束空间不同顶点间跳变，如图1（a）所示；而二次规划最优解在约束空间边界平面上平滑移动，如图1（b）所示，或为某个固定点，如图1（c）所示。

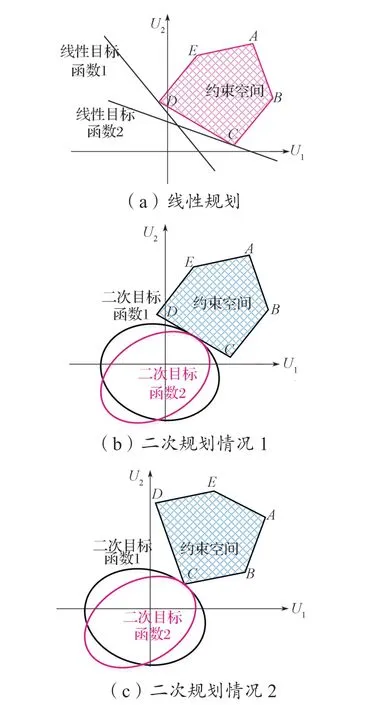
图1 不同权重系数对最优解的影响Fig.1 Influence of different weight coefficients on the optimal solution

2.2 代数关系分析

接下来以2 个MV、3 个CV 系统为例，从代数关系层面进一步验证上述方法。设所有CV 为同一级别，所有MV 都是代价变量，且硬约束空间内软约束无交集。如图2 所示，灰色矩形区域为硬约束；直线a和b，c和d，e和f分别围成的区域为软约束区间，可知所有约束条件没有交集，即不存在可行空间，可通过向上调整边界b、向下调整边界e、向下调整边界c，使区域S1 与S2相连。为使目标函数最小，即移动的距离尽可能小，最优策略是使直线b,e,c相交于一点，如图3 所示。

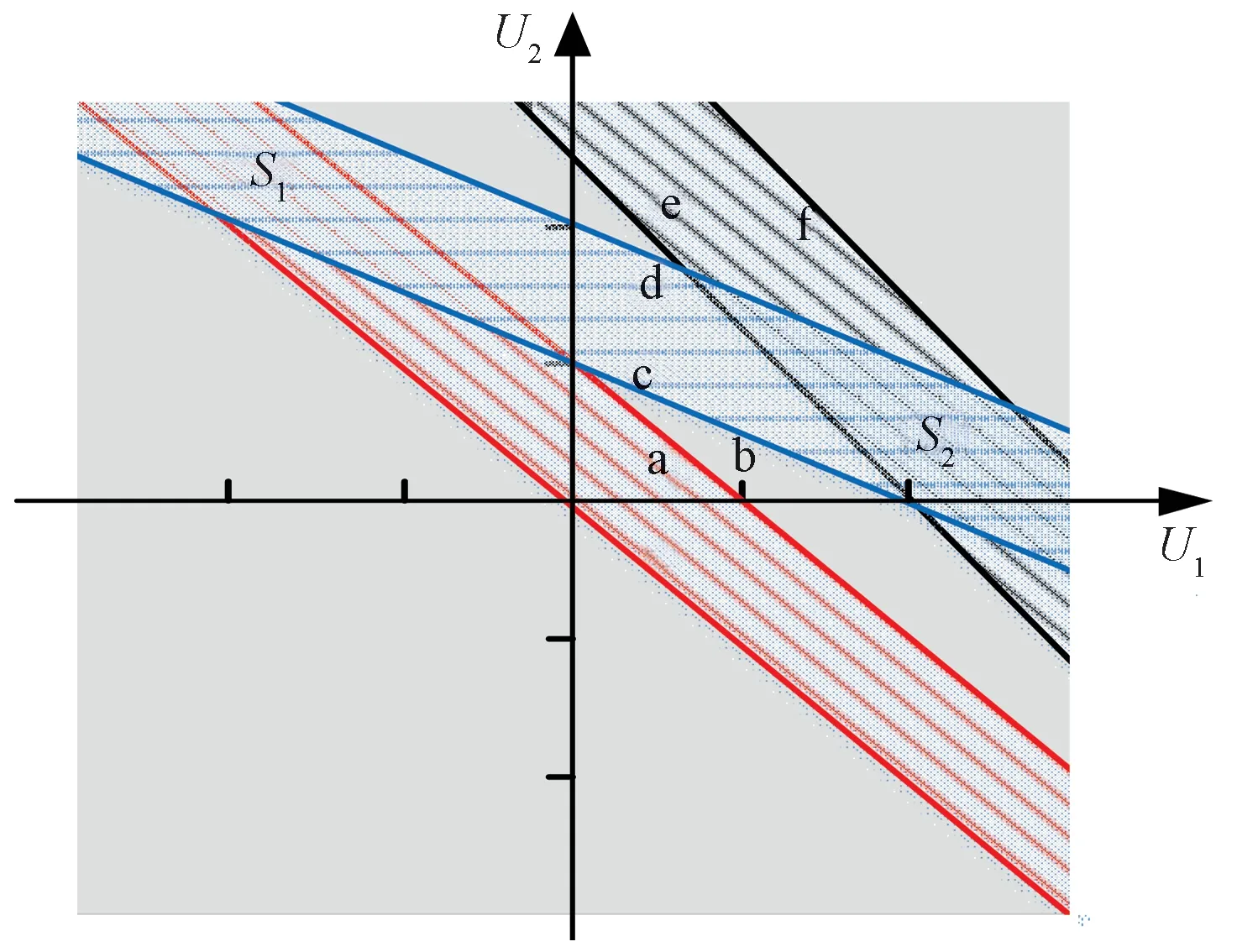
图2 约束条件几何关系图——不存在解空间Fig.2 Constraint geometry— no solution space

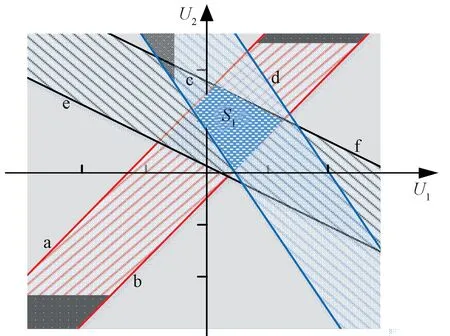
图3 约束条件几何关系图——存在解空间Fig.3 Geometric diagram of constraints—existence of solution space

此时，优化问题可简化为如下形式：

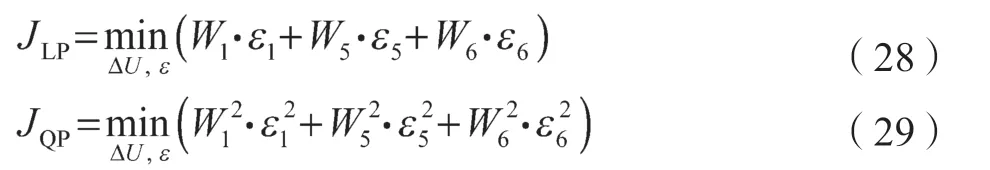
约束条件为

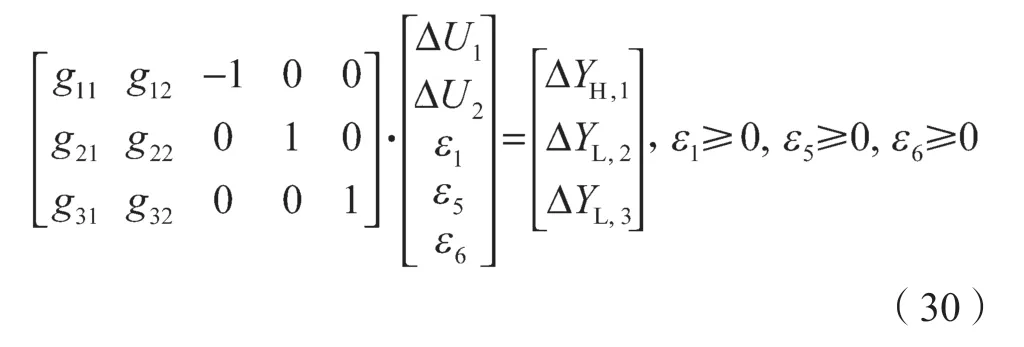
5 个决策变量、3 个等式约束条件且等式约束矩阵满秩，可以将等式约束条件简化为

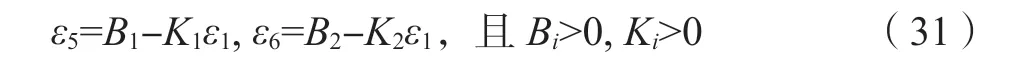
将式（31）代入目标函数式（28）和式（29），将优化问题化为单一决策变量优化：

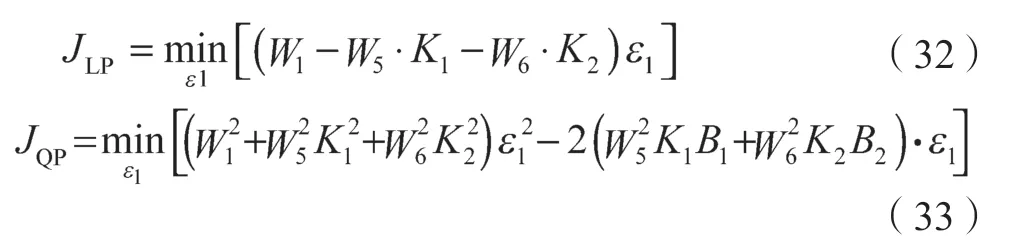
且满足

（1）对于LP

若W2-W5·K1-W6·K2＞0，则 最 优 值 为ε1=0,ε5=B1,ε6=B2；

若W2-W5·K1-W6·K2＜0，且B2K1-B1K2＞0，则最优值为ε1=B1/K1,ε5=0,ε6=(B2K1-B1K2)/K1；

若W2-W5·K1-W6·K2＜0，且B2K1-B1K2≤0，则最优值为ε1=B2/K2,ε5=(B1K2-B2K1)/K2,ε6=0；

若W2-W5·K1-W6·K2=0，则最优值为，ε5=B1-K1ε1,ε6=B2-K2ε1。

（2）对于QP

最优值为

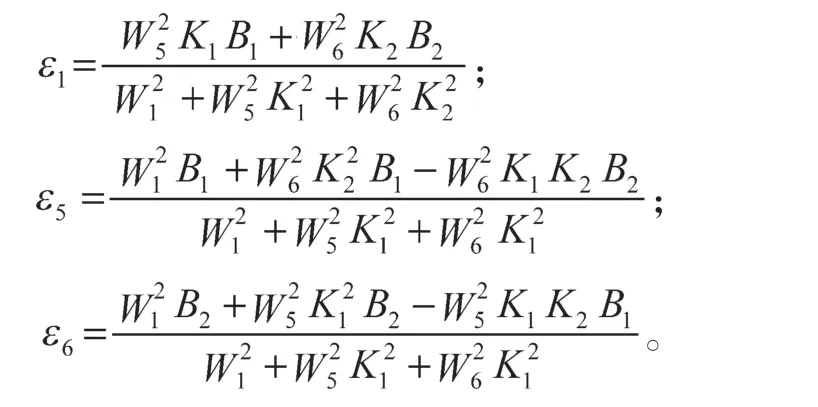
2.3 模型失配条件下解特性分析

实际应用中模型皆存在失配，即控制模型与实际对象存在不完全一致。双层MPC 采用滚动时域控制，由于存在模型失配，每个周期输出预测值与输出实际值间存在误差，如不进行修正，则误差累计造成控制误差甚至失稳。对此MPC 采用输出误差反馈校正输出动态预测序列及输出稳态值，抑制模型失配造成的控制波动问题。输出稳态值的校正公式如式（35）和式（36），其中e(k)为预测误差向量，即当前输出实际值向量与预测值向量之差。

稳定型CV 开环稳态预测值为

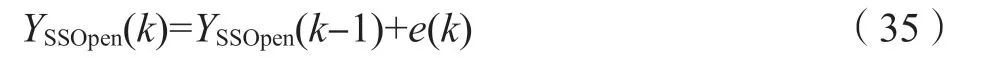
积分型CV 开环稳态斜率值为

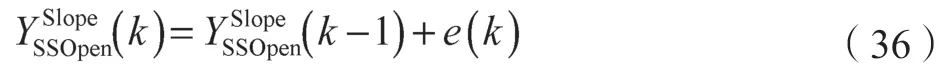
MPC 滚动优化过程中输出预测误差e(k)每个周期都在变化，因此输出稳态值也相应变化。结合式（9）可知，输出稳态值的变化仅改变约束边界B，不改变约束条件系数矩阵A。通过第2.1 节可知，若可行域有界，LP 的最优解一定在约束空间的顶点上，因此在滚动优化过程中，即随时间变化LP 的解一定会变化；而QP的解可能在约束空间的边界上、顶点上或内部，当解在边界上或顶点上时也会变化，若解一直在约束空间内部则不随时间变化。

2.4 结论

通过上述理论分析，可得到以下两个结论：

（1）由LP 与QP 的解的形式可知，当目标函数权重系数或者模型系数在一定范围内变化时LP 最优解保持不变，但随着权重系数或模型系数的连续变化，LP解会发生跳变，并且在LP 问题中权重并不能很好体现对决策变量的偏向；QP 的解随着权重系数或模型系数的变化而连续变化，并且权重能够很好地体现决策的偏向性。可见，QP 的权重能够更加精确地调节各个决策变量的偏向程度，而LP 的权重对偏向程度的反应相对比较粗略；但在求解过程中，由于QP 时间及空间复杂度皆高于LP 的。因此，实际工程中小规模的优化控制问题采用QP，更能体现优化的意愿；大规模优化控制问题采用LP，提高求解的快速性。

（2）由于实际工程中模型失配的存在，在滚动优化过程中，即随时间变化时，可行域边界的变化导致LP 的解一定会变化；若QP 的解在边界上或顶点上时也会变化，若QP 的解一直在约束空间内部则不随时间变化。

3 LP 及QP 解特性仿真分析

本节将通过随权重变化的解特性和模型失配时的解特性的仿真对上述结论进行验证。

3.1 随权重变化的解特性

将上述理论分析实例化，模型如式（37）所示，其中w1从1 至20 连续变化：

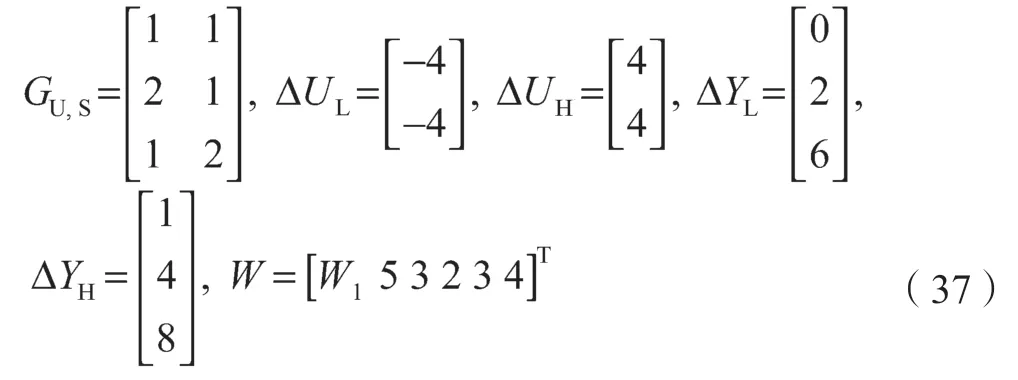
结合第1.2 节软约束松弛标准化过程，形成如下优化问题：

（2）约束条件

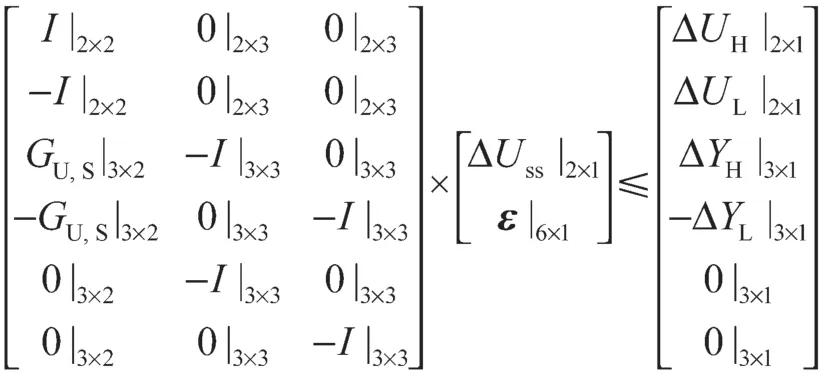
基于Matlab 编程，得到决策变量ε随权重W1连续变化的变化情况，具体如图4 所示，其中图4（a）和图4（b）的纵坐标ΔUi为操纵变量增量，图4（c）～图4（h）为各决策变量ε的QP/LP 解，下标H 代表ε的上限，L 代表ε的下限。

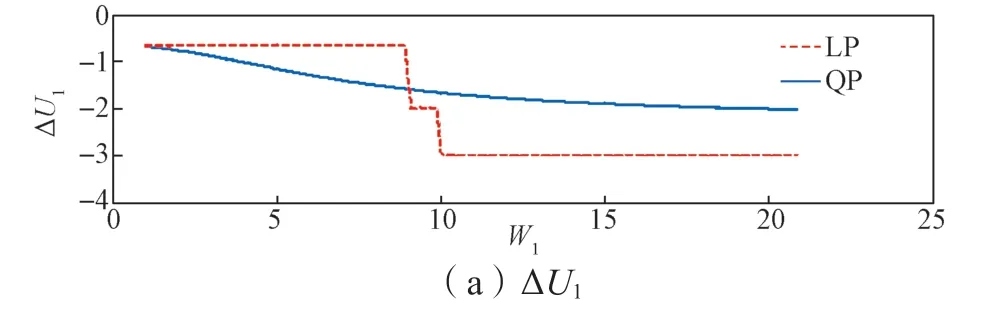
图4 最优解随权重变化曲线Fig.4 Curves of the optimal solution changes with weight

从图4 可见，当W1在8 和10 附近时，LP 的解发生跳变；当W1为其他值时，LP 解保持不变；QP 解随着W1的变化而连续变化，第2.4节所示理论分析结论（1）得到了验证。

3.2 模型失配时的解特性

采用第3.1 节模型，固定W=[2 5 3 2 3 4]T，仿真时间为100 个周期；并假设未校正输出预测值不变化，即MPC 处于开环状态，仅通过增加第一个输出预测误差反映实际模型失配；误差信号采用均值为0，幅值在[-1, 1]之间的随机值。仿真结果如图5 所示，图5（a）和图5（b）纵坐标ΔUi为操纵变量增量，图5（c）和图5（e）为各决策变量ε的QP/LP 解，图5（f）纵坐标e1为预测误差。可见， LP 与QP 解随着预测误差的变化而变化，且预测误差曲线与各个决策变量最优解的曲线变化趋势一致。图6 最优解与预测误差散点图进一步表明这种变化呈线性相关，即预测误差越大解的波动幅度越大，第2.4 节所示结论（2）得到了验证。

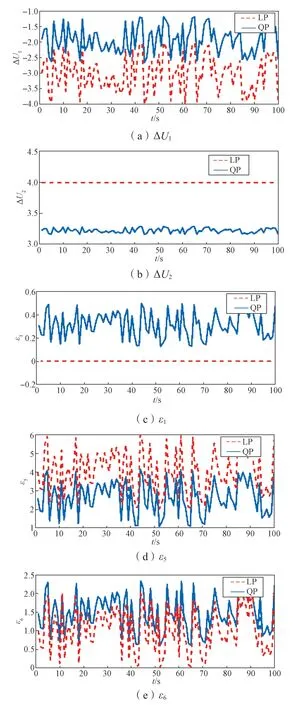
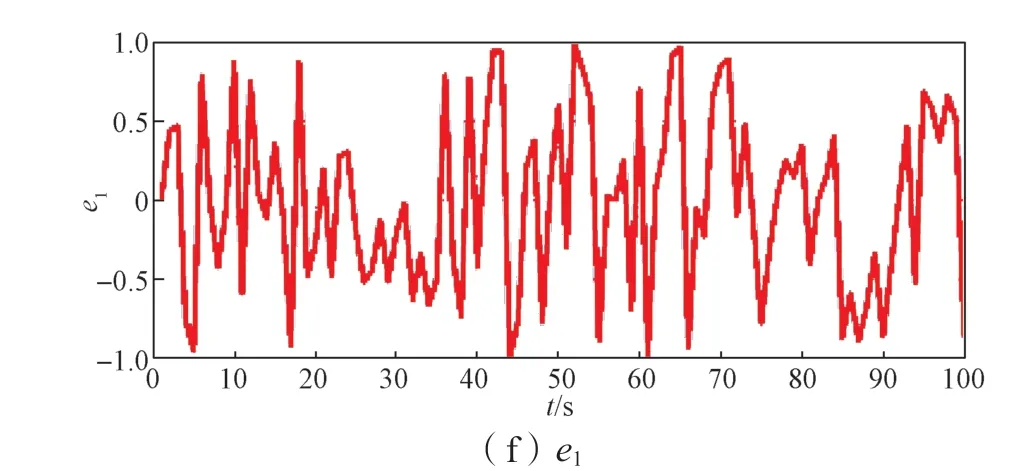
图5 模型失配下最优解随预测误差变化曲线Fig.5 Curve of the optimal solution changing with weight in the case of model mismatch

图6 最优解与预测误差散点图Fig.6 Scatter diagram of the optimal solution and prediction error

4 结语

本文通过对稳态优化理论的标准化、通用化研究，为预测控制的软件开发提供指导；通过对LP 及QP 最优解的特性分析，为工程应用中优化问题的策略选择提供了理论支撑。文中首先研究了双层结构预测控制的稳态优化层的两阶段法求解策略，将稳态优化问题转化为基于优先级的一系列标准LP 或QP 问题，并通过引入辅助变量解决了目标函数带绝对值的问题，最终形成可由计算机求解的通用描述形式；之后讨论了两阶段稳态优化求解策略中LP 及QP 解的特性，当目标函数权重系数在一定范围内变化时，LP 最优解保持不变，而QP 最优解随着权重系数的变化而连续变化。因此，QP 的解相比LP 具有更好的连续性，且QP 的权重能够更加精确地调节各个决策变量的偏向程度，而LP 的权重对偏向程度的反应相对比较粗略，并结合LP 与QP 的时间复杂度给出二者在工程应用中的选择原则；最后进一步讨论了模型失配对LP 与QP 解特性的影响，为实际应用中预测控制器稳态解的稳定性分析提供一定依据。 由于LP 与QP 算法求解将会随变量个数增大而变得复杂，如何在求解的过程中降低计算量是一个值得进一步研究的问题。