结合密度阈值和三角形组逼近的点云压缩方法

钟文彬，孙 思，李旭瑞，刘光帅

（1.中国电子科技集团公司第十研究所，成都 610036；2.西南交通大学机械工程学院，成都 610031）

（*通信作者电子邮箱912505671@qq.com）

0 引言

近些年来三维扫描技术迅速发展，逆向工程中可以获取的三维点云数据精度越来越高。随之而来的是点云数据规模也日益庞大。一旦数据量大的点云需要存储或通过速率受限制的通信通道进行传输，压缩操作就变得必不可少。压缩可以降低点云的冗余度，并用较少数量的点云表达模型的特征。

现有的点云数据压缩方法可以分为三类：基于网格拓扑信息的压缩、基于曲面拟合的压缩和基于点数据的压缩［1］。

基于网格拓扑信息的压缩一般是先预处理点云，获得网格模型，建立网格之间的拓扑关系，再对其进行压缩。Hur等［2］针对光固化立体造型（STereo Lithography，STL）文件，提出基于Delaunay 三角剖分的压缩方法，该方法在保证模型的精度上控制了时间成本；Kammerl等［3］提出用八叉树空间分解点云，通过构建点云的拓扑关系，编码无序点云流的八叉树结构的差异性来减少时空冗余度；方芳等［4］对点云先进行分层切片处理，然后对每层切片点云使用弦高差进行压缩；Houshiar等［5］提出将点云投影成全景图像，之后采用基于图像的方式压缩点云。这类方法压缩效果好，但是需要建立和维护大量的拓扑信息，计算量大，效率较低。

基于曲面拟合的压缩需要根据数据点集拟合一个曲面，利用曲面特性（曲率、法向量等）进行重采样。陈朋等［6］提出点到平面距离的无序点云压缩方法，该方法计算点到最近的三个邻域点组成平面的距离，通过距离的阈值来判断压缩对象表面的复杂程度；李金涛等［7］采用对数函数对归一化后的曲率值进行分级，对不同等级的点进行空间网格划分后分级压缩点云；宋敏峰等［8］根据点云的法向量构建K近邻（KNearest Neighbor，KNN）长方体，根据长方体扁平程度将点云分为非特征点云和特征点云，结合分段压缩去除大量冗余点和少量密集特征点。这类方法更易保留特征点，精度高，但由于需要求取采样点的隐式表达式，压缩速度较慢。

直接基于点数据的压缩，不需要建立拓扑关系和重建曲面，操作简单，压缩速度快。基本算法有比例压缩法、包围盒法、均匀网格法；但这些算法不能很好地表达细节特征，许多学者在此基础上提出改进。樊琦［9］改进了区域重心法，不仅保留栅格的重心点，还保留一个符合阈值范围的最远点；成煜钤等［10］通过设定不同的权阈值，进行点云的自适应压缩，但模型棱角特征遭到了破坏；Schwarz 等［11］针对静态点云，采用三角形组表达体素内点云表面信息，但不适用于非均匀采集点云。

通过上述分析，使用拓扑关系、法向量或曲率等信息决定压缩参数，计算时间较长，而基于点的压缩方法，多适用于特征简单的均匀点云。针对非均匀点云的压缩中压缩精度和压缩时间较难权衡的问题，本文提出一种结合密度阈值和三角形组逼近的点云压缩方法。结合点云分布，分别确定密集区域和稀疏区域内三角形组的顶点和细分点，再利用三角形组模拟原始体素内点云表面。

1 三角形组逼近

因为三角剖分能为曲面重建提供最小的形状单位，故常用于点云曲面重建。实际情况下，运用最多的是Delaunay 三角剖分。Delaunay 三角剖分旨在寻找到一个最优的三角剖分，满足空外接圆和最大-最小角特性。空外接圆指的是每个三角形的外接圆内部没有其他点；最大-最小角指的是所有三角形的最小角达到最大。

点云库（Point Cloud Library，PCL）中的贪婪投影三角化算法在二维上使用了基于Delaunay 的空间区域增长算法，先建立初始三角形，再扩展三角形网格［12］。如图1 所示，ΔABO是已经确定的三角形，C和D是备选顶点，分别连接对角线BC和AD，可以得到对应两个三角形的角度序列：

比较可以得到AD＞BC，所以，选择D作与AB组成三角形的顶点。

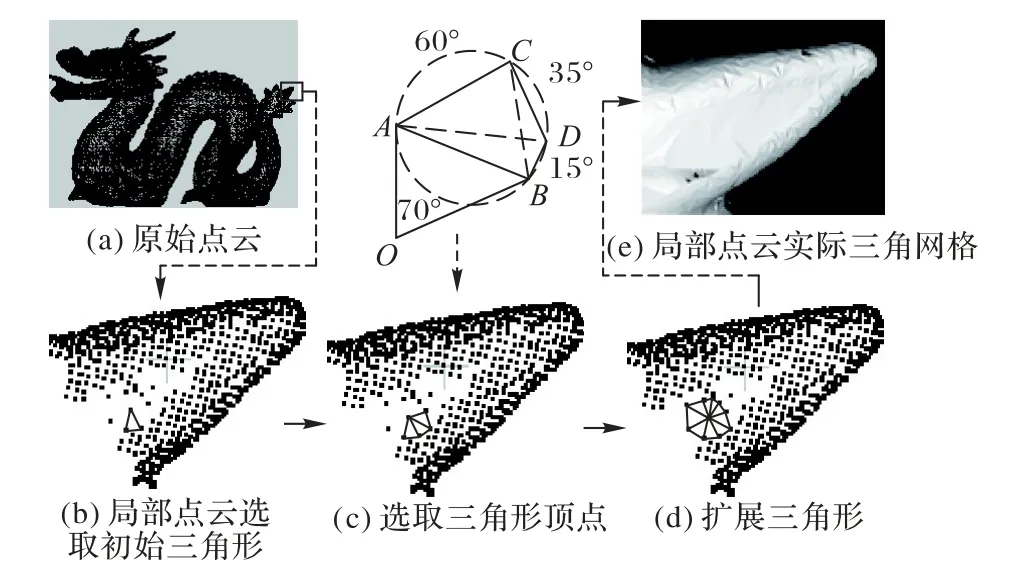
图1 三角形扩展Fig.1 Extension of triangle

本文使用三角逼近的思想，先将点云划分为大小统一的体素；然后，将体素内点云投影到某一平面上进行三角形组构造。在三角形组逼近点云表面的基础上，用三角形组的顶点和细分点代替三角形网格信息。这样不仅可以节省构建网格的时间，还可以有效地压缩点云数据。

2 算法描述

2.1 坐标转换

如图2 所示，通过扫描仪获得的点云数据表示为浮点数类型，既有正数也有负数。因为后续计算细分点的坐标时，需要的数据类型是正数，所以压缩之前需先转换坐标。

图2 坐标转换Fig.2 Coordinate transformation

2.2 建立八叉树

利用PCL中的pcl：：octree：：OctreePointCloud函数初始化八叉树，以便存储和遍历点云数据。八叉树通过人为指定分辨率初始化，分辨率描述的是最低一级八叉树的最小体素的实际尺寸。通过分析可以找到合适的分辨率，以达到合适的压缩效果。对本文实验对象，dragon 点云选取0.002 作为最小体素尺寸；horse点云选取0.003作为最小体素尺寸；skull点云选取0.3作为最小体素尺寸；radome点云选取0.002 8作为最小体素尺寸；dog 点云选取1.5 作为最小体素尺寸；印制电路板（Printed Circuit Board，PCB）点云选取0.0025作为最小体素尺寸。

2.3 八叉树体素内点云压缩

点云使用八叉树进行空间分割，其中，八叉树叶节点的个数即是体素的个数。体素内无复杂特征时，体素内点可以投影到一个与坐标轴垂直的平面上，保持邻接关系不变。投影点云与原始点云得一一对应，保证了二维各点的连接关系对应三维各点的连接关系。如图3 所示，体素内部压缩具体步骤分为确定三角形顶点、确定顶点分布信息、顶点排序、三角形构造和细分点构造。同时对应算法流程如算法1 所示，其中输入包括体素内所有三维点的坐标集合Pint、密度阈值(thr1与thr2)和体素的几何信息Voxel；输出为压缩后三维点的坐标集合。

图3 压缩流程Fig.3 Compression flowchart

2.3.1 确定三角形顶点

计算投影点的平均值qk。原始点云中距离qk最近的点即是lk对应的顶点vk。遍历体素的每一条边，如图3（c）所示，确定体素内三角形的所有顶点。

图4 计算顶点Fig.4 Calculation of vertices

2.3.2 确定顶点分布信息

确定顶点分布信息的第一步是根据顶点向量V计算顶点质心μ=(μx，μy，μz)，并进行主导轴判断。确定主导轴，即是确定投影方向。如图5 所示，分别将体素边缘上的顶点沿x轴、y轴和z轴投影。结果显示，沿x轴和z轴得到的投影图出现了多个点投影到同一个位置的现象（图5中空心点），为使得投影面上各点分散开，故选择方差分量最小的轴作为主导轴［12］。根据

计算顶点到质心的方差。其中：n是顶点的数量；对应轴即是主导轴。

图5 投影顶点Fig.5 Projection of vertices

第二步是将每个顶点投影到主导轴上，计算顶点分布信息vk.infor。如图3（d）所示，顶点分布信息包含位置参数ai、bi和ci。其中，ci表示在主导轴方向上顶点与体素中心的距离；ai和bi表示其他两轴上顶点与体素中心的距离。例如，则z是主导轴，则有ci=zi-mz、ai=xi-mx和bi=yi-my，其中m=(mx，my，mz)是体素的几何中心。

最后一步是根据顶点的分布信息vk.infor计算顶点的角度vk.θ，即：

2.3.3 顶点排序

顶点角度vk.θ是顶点排序的依据。如图6所示，将顶点投影到与主导轴垂直的平面上，降序排列顶点角度vk.θ。

图6 顶点角度Fig.6 Angles of vertices

排序不仅有利于顶点的快速提取，还指定了三角形组逼近中遍历顶点的顺序。如图3（e）所示，将散乱分布的顶点根据角度vk.θ的顺序进行编号。

2.3.4 三角形构造

本文方法利用排序后的顶点列表对每个非空体素进行三角形组的构造。由于点云的表面是连续的，故在三角形组构造时，应避免体素内模拟的三角形表面与邻近体素内的表面不连贯。因此，三角形组的边缘线，即点云与体素表面的相交线，一定位于体素表面上。如图7（a）和图7（b）所示，边缘线（虚线）悬空于体素内部，不与邻近体素接触，正确的边缘线如图7（c）所示。

由于体素每条边上最多一个顶点，故排序后的顶点列表中，相邻两个点在体素同一个表面内，但连续的三个点不在同一个表面内，如图8 所示。Mammou 等［13］利用这一特性，直接连接顶点列表中的相邻点作为三角形组的边缘线，而相邻边缘线对应的三个顶点将构成一个三角形，如表1 所示。这样构造出的三角形组，其边缘线一定在体素表面上，保证了相邻体素三角形组的连贯性。图8 显示表1中具有5 个顶点的体素构造三角形组的过程。在投影面上得到降序排列的顶点列表后，前三个顶点（1、2 和3）组成一个三角形。每组成一个三角形，就将该三角形中间顶点（2）从列表删除，第一个顶点（1）移至列表末尾，重复取列表的前3 个点构造三角形直至列表为空。

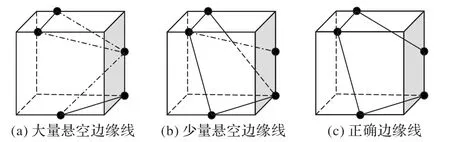
图7 三角形组的边缘线Fig.7 Edge lines of triangle groups

图8 体素内三角形组的构成Fig.8 Formation of triangle groups in voxel

表1 三角形组的构成Tab.1 Formation of triangle groups

2.3.5 细分点构造

细分点指的是三角形内部的点，其作用是避免三角形重构时发生混淆。如算法1中RaysParallelToCoordinateAxi函数所示，细分点构造需要在每个三角形内构造平行坐标轴6个方向的射线，即(1，0，0)、(0，1，0)、(0，0，1)、(-1，0，0)、(0，-1，0)、（0，0，-1）。射线的起点取决于三角形三个顶点分别在x轴、y轴和z轴上的最小值和最大值(xmin，xmax，ymin，ymax，zmin，zmax)，构造起点的步长受体素密度控制，如getStepSize函数所示。在体素尺寸固定的情况下，体素密度是体素内点数的一元函数。本文方法以体素内点云点数作为密度指标，密度小使用大步长，密度大使用小步长。例如，构造沿x轴正方向的射线时，如图3（g）所示，射线起点的坐标在x轴上的分量等于xmin，y轴上的分量在范围(ymin，ymax)内，z轴上的分量在范围(zmin，zmax)内。每条射线与三角形的交点，即是新的细分点。

算法1 体素内压缩算法。

3 实验与分析

选择dragon 点云、horse 点云、skull 点云、radome 点云、dog点云和PCB 点云，对本文方法进行实验、分析和评价。其中，dragon 点云、horse 点云、skull 点云和dog 点云取自斯坦福经典点云数据库，而radome点云和PCB点云是通过FreeScan X5激光手持三维扫描仪扫描得到的点云数据。各点云相关信息如表2所示，原始点云可视化如图9所示。

表2 原始点云信息Tab.2 Information of original point cloud data

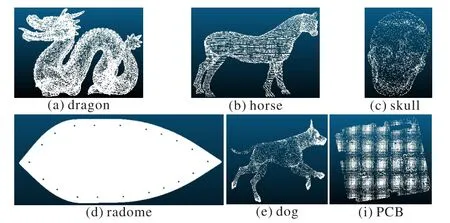
图9 原始点云Fig.9 Original point clouds

dragon点云分布比较不均匀，细小特征多；horse点云分布较均匀，密度较小，特征少，多为大区域曲面；skull点云分布极其不均匀，面部区域细小特征多且密度大，后脑勺区域特征少且密度小；radome 点云分布较均匀，密度最大，特征少；dog 点云分布极不均匀，复杂特征集中在面部，同时具有尾巴等细长特征；PCB点云分布较不均匀，直角特征多。

实验使用系统Windows 7，CPU 为Inter Core i5-4590 CPU，内存为16.0 GB。

3.1 体素尺寸

因为少于3 个顶点的体素不构造三角形，所以，为了避免次特征部位（例如dragon 点云龙鳞部位和skull 点云脸颊部位）体素内点过少，细分三角形效果不佳，体素的实际大小不宜过小；同时，为了避免密集部位特征不能完整表达，体素实际大小亦不宜过大。

如图10 所示，dragon 点云、horse 点云和radome 点云随着体素大小的增加，顶点少于3 个的体素占总非空体素的比例趋向于0。

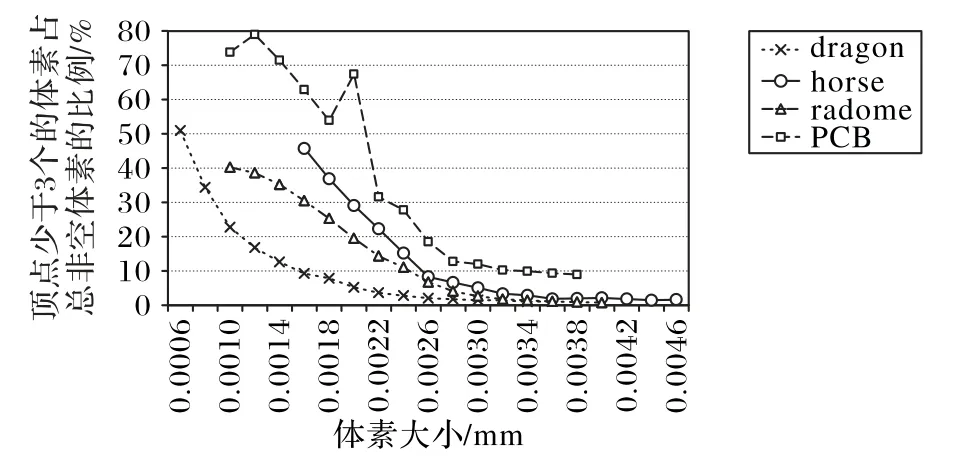
图10 dragon、horse、radome和PCB点云中顶点少于3个的体素占总非空体素的比例Fig.10 Proportion of the number of voxels with fewer than 3 vertices to total number of non-empty voxels in dragon，horse，radome and PCB point clouds

而针对skull 和dog 点云，从图11 可以得到顶点少于3 个的体素占总非空体素的比例没有趋向稳定，这是因为原始数据分布极不均匀，skull 点云后脑勺部位和dog 点云身体部位点云密度小，大多不能构造三角形。

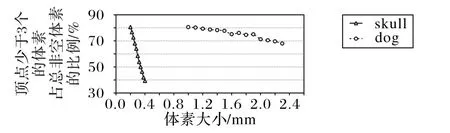
图11 skull和dog点云中顶点少于3个的体素占总非空体素的比例Fig.11 Proportion of the number of voxels with fewer than 3 vertices to total number of non-empty voxels in skull and dog point clouds

结合图12（a）和12（b），dragon点云的龙身部位，在体素大小达到0.003 2时，体素内的弯曲特征不能通过构造三角形组表达出来，而体素大小是0.001 6时，体素内点分布无弯曲。所以，将体素大小控制在0.001 6 附近，以压缩后所建模型的表面积变化率为指标，进一步分析最优尺寸，结果如表3 所示。表面积变化率是将压缩前和压缩后的点云生成三角面片模型，并计算和比较两个模型之间的表面积差异。为保证压缩后模型与原始模型最接近，选取0.002 作为dragon 点云后续实验的体素尺寸。

同理，为保证三角形顺利构造的同时不丢失明显特征信息，根据图10、图12（c）、图12（d）和表3，选择0.003作为horse点云后续实验的体素尺寸；根据图10、图12（g）、图12（h）和表3，选择0.002 8作为radome点云后续实验的体素尺寸。

而PCB 点云对应曲线在体素大小等于0.001 2 和0.002时具有两个凸脊，这是因为原始点云在边缘处具有少量孔洞，如图9（i）所示。但体素大小大于0.002 后，随着体素大小的继续增加，顶点少于3 个的体素占总非空体素的比例开始收敛。结合图10、图12（k）、图12（l）和表3，选择0.002 5 作为PCB点云后续实验的体素尺寸。

图13 为skull 点云脸颊部位和dog 点云身体部位不同尺寸体素内点的分布。

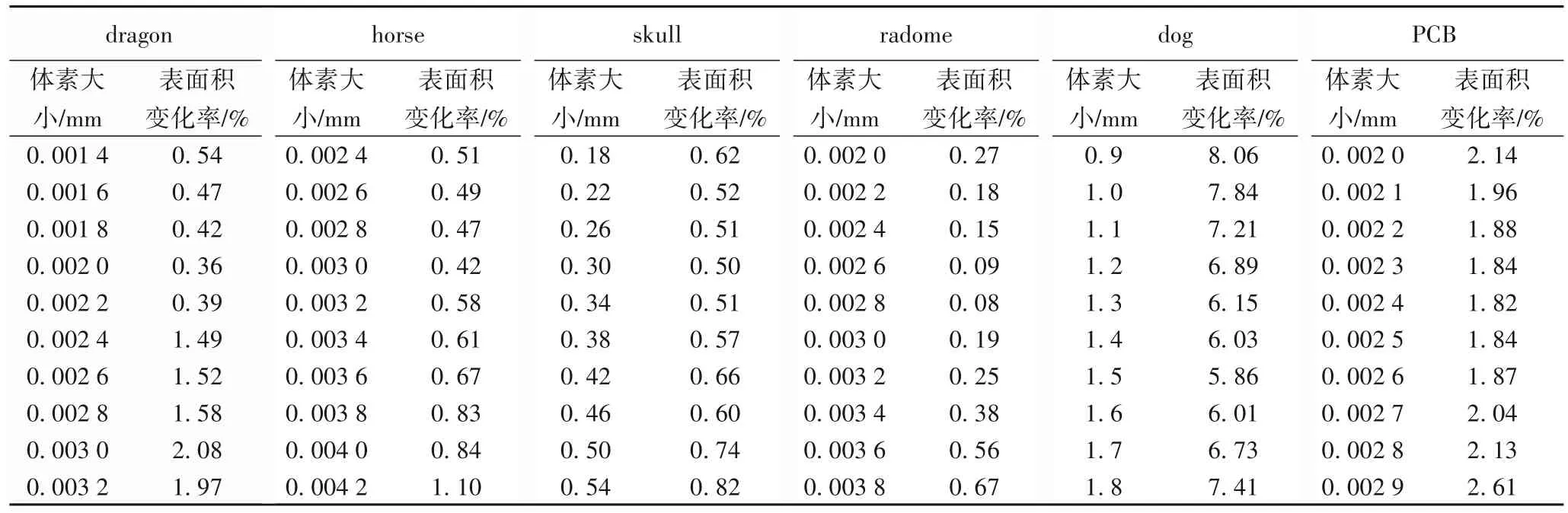
表3 使用不同尺寸体素压缩后的表面积变化率（不考虑细分点）Tab.3 Change rate of surface area after compression using voxels with different sizes（subdivision points are not considered）

图12 原始点云特征部位不同尺寸体素内点的分布Fig.12 Distribution of points in voxels with different sizes of feature regions of original point clouds

图13 skull点云脸颊部位和dog点云身体部位不同尺寸体素内点的分布Fig.13 Distribution of points in voxels with different sizes of cheek region of skull point cloud and the body region of dog point cloud

根据图13（a～d）观察到，skull 点云脸颊凹陷部位，在体素大小为0.08和0.16时不能构造三角形；而图12（e）和图12（f）显示，体素大小为0.64时，点云额头符号处特征不能较好表达，所以，将体素大小控制在［0.16，0.64］内，以压缩后所建模型的表面积变化率为指标，进一步分析最优尺寸，结果如表3所示。最终，选择0.3 作为skull 点云后续实验的体素尺寸。同理，根据图13（e～h）、图12（i～j）和表3，选择1.5 作为dog 点云后续实验的体素尺寸。

3.2 密度阈值

在确定体素大小后，如图14 所示，以二分之一体素尺寸为半径，观察原始数据点的邻域点信息。该邻域信息可以大致反映出整体点云的密度情况，有助于密度阈值的选取。密度阈值不仅可以区分稀疏区域、较密集区域和密集区域，也可以区分特征程度。密集区域特征复杂，稀疏区域特征简单。稀疏区域用最大的步长构造射线，密集区域用最小的步长构造射线。射线的构造影响细分点的数量，使得压缩后稀疏区域依旧比密集区域密度小，用较少的点表达较少的特征。

dragon 点云在龙身蓝色部位特征少，邻域点数不多于7个；在大面积的绿色部位，特征信息明显增加，邻域点数不多于28；在黄色或红色区域，特征最复杂，邻域点个数最多，甚至有的区域达到了40 个邻域点。为将稀疏区域（蓝色）和密集区域（黄色和红色）区分开，选取［8，12］作为区分稀疏区域和较密集区域的阈值1（threshold1，thr1）范围，同时选取［23，27］作为区分较密集区域和密集区域的阈值2（threshold2，thr2）范围。分析thr1时，以固定thr1 的情况下使用不同thr2压缩后所得模型的平均表面积变化率为指标。同理，分析thr2时，以固定thr2的情况下使用不同thr1压缩后所得模型的平均表面积变化率为指标，结果如表4 所示。为使压缩后所得模型与原模型更接近，根据表4，选取10 和25 作为区分稀疏区域、较密集区域和密集区域的阈值。

horse点云蓝色部位较少，邻域点数不多于7个；大部分点位于绿色区域，其邻域点数在9 个以下；黄色或红色特征区域邻域点数在10 个左右。所以，选取［6，8］作为区分稀疏区域和较密集区域的阈值范围，同时选取［9，11］作为区分较密集区域和密集区域的阈值范围。根据表4，选取7 和11 作为密度阈值。

同理，skull 点云根据图14（c）中的邻域信息和表4 的平均表面积变化率，选取4 和8 作为密度阈值；radome 点云根据图14（d）中的邻域信息和表4 的平均表面积变化率，选取18和28作为密度阈值；PCB点云根据图14（f）中的邻域信息和表4的平均表面积变化率，选取15和25作为密度阈值。

同时，从图14（e）中的邻域信息可以得到，dog 点云大部分处于蓝色区域（身体部位），邻域点个数不超过7 个；只有少量点位于黄绿色区域（面部和脚掌）和红色区域（眼睛），但邻域点个数较多。所以，只选择［7，11］作为区分密集区域和稀疏区域的阈值范围。根据表4，选择7作为密度阈值。

图14 原始数据邻域点个数Fig.14 Number of neighborhood points of original data

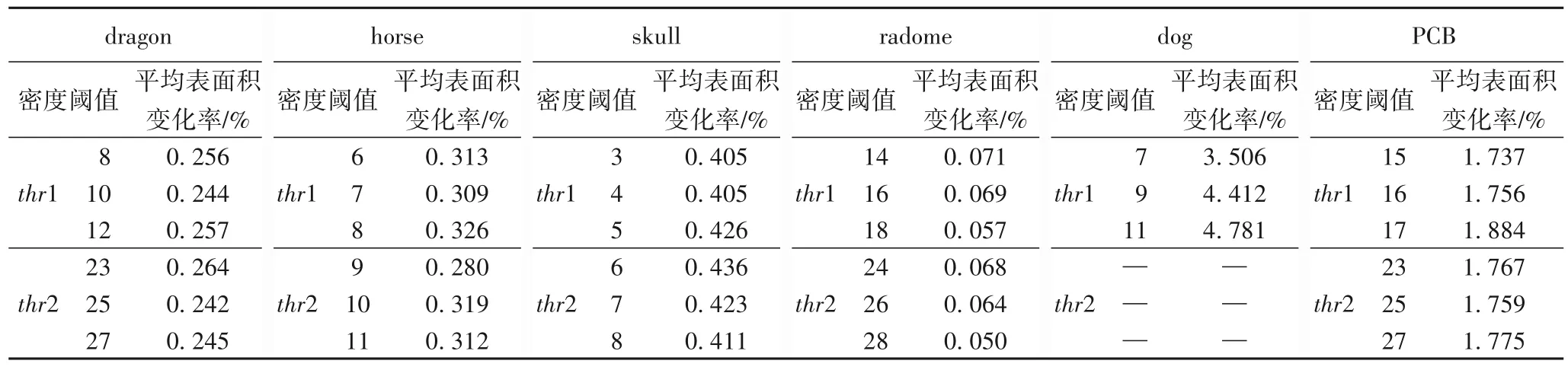
表4 原始点云使用不同阈值压缩后所得模型的平均表面积变化率Tab.4 Mean value of surface area change rate of the models obtained by original point clouds compressed with different threshold values

3.3 结果分析

分别用改进区域重心法［9］、曲率压缩法［14］、改进曲率分级法［7］、K近邻长方体法［8］和本文方法对原始数据进行处理。区域重心法的栅格大小和3.1 节提到的各点云体素大小一致；曲率压缩的方法，保证压缩率与本文方法大体一致；改进曲率分级压缩中特征区域尺寸与3.1 节提到的各点云体素大小一致，保证分析点云特征时最小单元一致；K近邻长方体法取α=0.8，同时控制压缩率与本文一致。

从表5 和表6 知，在体素大小一致的情况下，改进区域重心法比本文方法压缩更多的点，时间更快。在压缩率接近的情况下，曲率压缩法、改进曲率分级法和K近邻长方体法需要比本文更多的时间，这是因为这三种方法在计算曲率或法向量上消耗了大量时间。同时，表5中使用改进曲率分级法对skull 和dog 点云压缩时，剩余点数高于本文方法，这是因为受特征区域尺寸限制，记录的是压缩率最大（压缩因子最小）时剩余点数。即使如此，由于改进曲率分级法中主要耗时在于曲率计算和曲率对数化，压缩率变化对耗时影响较小，故表6中skull和dog点云使用改进曲率分级法的耗时远高于本文方法，也能侧面印证本文方法在时间效率上优于改进曲率分级法。所以，在时间效率上，本文方法介于改进区域重心法和需要计算曲率或法向量的方法之间。

表5 压缩后剩余点数对比Tab.5 Comparison of remaining points after compression

观察6 种方法结果，分别对压缩后的数据使用geomagic studio12 软件封装显示，并使用最大偏差、标准偏差和表面积变化率进行分析。图15～16 为6 种点云数据的geomagic 封装示意图。

图15 dragon、horse和skull点云geomagic封装示意图Fig.15 geomagic package schematic diagrams of dragon，horse and skull point clouds

图15（a～f）显示，dragon 点云经过改进区域重心法压缩，模型的头部、脖子和背鳍部分细节丢失，整体效果极差，而通过曲率压缩、改进曲率分级法、K近邻长方体法和本文方法得到的模型大部分特征保留。同时，本文方法压缩后的模型相较于曲率压缩和K近邻长方体法在细小特征上（椭圆部分）有较好效果。图15（g～l）显示，horse 点云使用改进区域重心法模型头部失真，并且在模型脚部（图15（g）黄色部位）因数据丢失过多造成相邻区域法向量方向不同。同时，K近邻长方体法压缩后所建模型在脚部明显比原始数据粗糙，而曲率压缩、改进曲率分级法和本文方法所建模型与原始模型更接近。图15（m～r）显示，skull点云通过5种方法得到的模型都出现不同程度的失真，但在整体效果和牙齿等特征部位，本文方法效果最好。

图16（a～f）显示，radome点云使用改进区域重心法效果最差，不仅表面粗糙还有大面积孔洞（图16（a）绿色线条圈出部位）；曲率压缩后所建模型有少量孔洞和相邻区域法向量方向不同现象；改进曲率分级法效果稍好，但仍有相邻区域法向量方向不同现象；本文方法和K近邻长方体法效果与原数据效果最接近。图16（g～l）显示，dog 点云原始数据所建模型在尾部因密度小，有断层情况；曲率压缩和K近邻长方体法所建模型出现腹部断层，这是因为该区域过度压缩，造成点云密度过小，不能成功封装，如图17 所示；改进区域重心法和改进曲率分级法压缩后尾部发生变形；本文方法压缩后不仅无过度压缩情况，而且尾部形状较完整。图16（m～r）显示，PCB 点云使用改进区域重心法效果最差，K近邻长方体法稍好，但在边缘处出现孔洞，而改进曲率分级法和本文方法压缩后得到的模型与原始模型更接近。

表7 反映出5 种方法压缩后的最大偏差和标准偏差。偏差分析可以显示出测试模型和参考模型之间的空间差异。其中，最大偏差测量的是测试模型到参考模型中任意点的距离的最大值，而标准偏差反映了整体模型的偏差情况，偏差越大则测试模型与参考模型差异越大。其中，dog点云因为使用曲率压缩法和K近邻长方体法压缩后得不到反映实际特征的模型，不考虑相应偏差。针对6 种点云数据，通过本文方法得到的最大偏差皆低于改进区域重心法、曲率压缩法、改进曲率分级法和K近邻长方体法。在标准偏差上，dragon 和PCB 点云标准偏差都是0；horse 点云基于改进区域重心法标准偏差最高；skull 和dog 点云压缩前后都有标准偏差，这是因为密度小的区域压缩发生了变形，但本文方法的标准偏差小于其他方法；radome点云本文方法标准偏差最小。数据显示，本文方法对于密度较大的点云，压缩后点云更接近原始点云。

图17 dog点云示意图Fig.17 Schematic diagrams of dog point cloud

同时，本文使用表面积变化率分析点云压缩精度。假设原始点云建模得到的表面积为真值，表面积变化率可以近似反映点云压缩的精度［8］。表8显示，压缩前后表面积变化率是区域重心法最高，本文方法最低，验证了本文方法比其他方法效果好。

通过对比不同方法可以得到，本文方法在高压缩率的情况下，可以保留原数据点云绝大多数特征，所建模型与原始点云模型最接近，整体压缩效果良好。

表6 压缩时间对比Tab.6 Comparison of compression time

表7 最大偏差和标准偏差对比Tab.7 Comparison of maximum deviation and standard deviation

表8 表面积变化率对比Tab.8 Comparison of surface area change rate

4 结语

针对非均匀采集点云数据压缩中压缩精度和压缩时间较难权衡的问题，本文提出了一种结合密度阈值和三角形组逼近的压缩方法。该方法在八叉树划分的基础上，对每个非空体素构造三角形组逼近体素内点云表面，并采用密度阈值决定三角形细分点的步长；通对对点云在不同体素尺寸下能够构造三角形组的体素占总体素的比例和体素内部点的分布分析，选择合适的八叉树分辨率；通过对点云的邻域分析，选择相应密度阈值。针对dragon、horse、skull、radome、dog 和PCB点云，分别进行改进区域重心法、曲率压缩法、改进曲率分级法、K近邻长方体法和本文方法的压缩对比实验。实验结果显示，区域重心法速度最快，压缩率最高，但特征丢失多，偏差最大，表面积变化率最大；曲率压缩速度较慢，特征保留较完整，有非特征区域过度压缩情况，偏差和表面积变化率较大；改进曲率分级法速度较慢，特征保留完整，偏差和表面积变化率小于曲率压缩；K近邻长方体法速度最慢，有非特征区域过度压缩情况，偏差和表面积变化率小于改进区域重心法；本文方法速度适中，特征保留完整，偏差和表面积变化率最小。实验验证了本文方法可以在较短的时间内较好地保留特征信息。

本文方法是通过数据分析后人为选取合适的八叉树分辨率和密度阈值，下一步将在该方法的基础上，进一步研究参数的自适应设定。