点云数据的凹陷体判定算法
杨作威 车 明
(天津大学智能与计算学部 天津 300350)
0 引 言
物体具有长、宽、高的三维物理尺寸。然而,大多数显示技术仍然属于二维显示技术,包含一些深度线索,但缺乏深度信息,这将导致人眼的深度、动态和视差功能的退化[1]。因此人类的大脑需要获取完全符合三维真实物体的信息,也就是三维信息。体三维显示是三维显示领域的重要研究方向,为人类视觉系统提供生理和心理深度信息以感知3D对象,可允许多个观察者同时从不同角度观察到同一三维场景的不同侧面[2]。但是当体三维显示系统处理带凹陷体的点云数据时,由于凹陷体区域无法正确判定,导致对应区域的颜色缺失,会影响体三维系统的显示效果。而现有的相关点云处理算法主要是对点云边界的判定与处理。3D点云中边界的提取方法可分为两类,分别是基于网格的方法和直接基于点的方法。基于网格的方法可以通过网格之间的拓扑关系来识别边界[3-8]。Jun[5]利用边界三角网格的相邻三个网格中至少一个为空的原理确定种子边界点,再通过跟踪获得闭环边界边,但是无法区分模型外边界和内部空洞边界。Huang等[6]首先对点云构建tin网格,初始化一个最大边界,再通过设立网格边长阈值逐步缩小边界边,最终得到精确的点云边界,该算法适合于处理复杂形状的点云数据。直接基于点的方法首先找到每个点的邻居,然后通过计算点的几何属性如法向量、密度等以确定边界[9-14]。丁承君等[10]首先构造点云kd树拓扑结构,通过RANSAC算法寻找种子点确定平面,并找出感兴趣区域,最后通过k邻域点的法线夹角与阈值对比确定边界点。Gai等[11]使用二维相位图和每个点的相邻区域来确定边界,然后使用边界点的行和列坐标删除轮廓点。陆帆等[12]首先将每个目标点及其相邻点投影到平面上,然后计算反距离权重和点云密度来确定其是否为边界特征点,但是算法依赖加权权重的选取。除此之外,Bao等[15]借助3D laser scanner将三维点云映射到二维range图像中,利用图像处理中的canny算子得到点云边界,但是算法无法区分内外边界。
现有的点云边界算法只能识别孔洞或点云的边界,缺乏对凹陷体判定的研究,因此,本文工作如下:(1)提出了凹陷体的定义,并为之做出了形象化的描述;(2)根据凹陷体的空间特性,提出了基于空间连通性原理的凹陷体判定算法,为点云中凹陷体的判定提出了一种解决方案;(3)通过实验验证了算法的可行性并对未来的应用前景做出了展望。
1 凹陷体判定算法
1.1 凹陷体定义
本文将凹陷体定义以y轴作为高度轴,凹陷体是指处于点云模型中,或不含点的空间,凹陷体与点云外界区域相被点所包围,且高度值低于点云中周围点的高度变化趋势,含少量点连通。如图1所示,图1(a)为点云数据,图1(b)三部分点云分别包裹的区域即为凹陷体,而点云内部的空洞由于不与外界连通,不属于凹陷体。本文针对该问题提出了PCDD算法以求出点云中的各个凹陷体,为后续的应用打下基础。
(a)点云数据 (b)凹陷体边界图1 点云凹陷体示意图
1.2 凹陷体判定算法原理
凹陷体判定算法流程如图2所示。
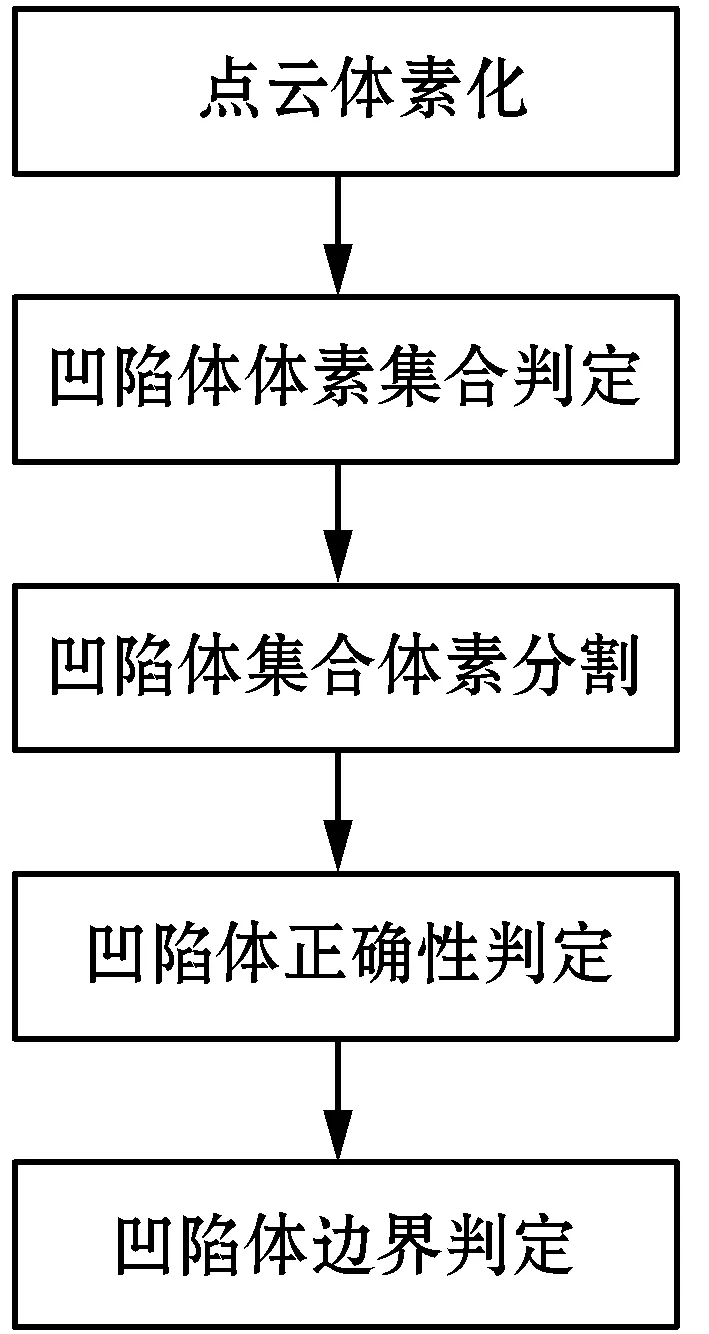
图2 凹陷体判定算法流程
1.2.1点云体素化
1)确定点云体素化分割大小。计算出点云数据在x、y、z轴上的范围,分别记作range_x、range_y、range_z。取三者其中的最小值记作min并将其k等分,其他两个方向上按照相同比例进行分割,其中k取决于实验经验值。
2)构建外表面层作为凹陷体正确性判定依据。由于在点云数据中,点只分布于实体边界周围而实体内部通常是没有点的,因此在本文的算法处理过程中模型内部的空洞也会被判定为凹陷体。对于这种模型本身的空洞及模型所包含的真实凹陷体如果不加以区分的话会造成判定错误。因此,本文考虑到真实的凹陷体是与点云外界区域相连通的原理,通过在点云的外表面附加一层体素来作为连通性判定的依据。将y轴作为点云数据的高度轴,点云体素化示意图如图3所示。
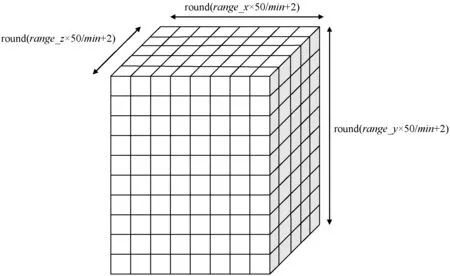
图3 点云体素化示意图
3)定义体素及平面区域结构体。对于每一个体素,本文定义其结构体如下:
struct VOXEL
{
introw,col,height;
//体素所处的空间位置坐标:行,列,高度
intsize;
//体素包含的点个数
intlabel;
//label为-2表示体素内包含点数大于阈值,label为-1表示
//体素为判别连通性的附加表面层,label为0表示体素包含点
//数小于阈值,label为大于0的自然数表示属于各个不同凹陷
//体。初始状态下体素label只有0、-1、-2三种
}
同时在xz平面方向上定义结构体:
struct grid
{
intmax_height;
//该区域的最大高度
VOXEL *voxel;
//存储该区域在高度方向上的体素,
//数组大小为round(range_y×k/min)+1
}
4)定义点云中点的空间位置。计算每个点所处的体素位置,记第i个点的三维坐标为(xi,yi,zi),记整个点云文件的x、y、z最小值分别为x_min、y_min、z_min,第i点所处矩阵的行:
round((zi-z_min)/(range_z/round(range_z×k/min)))+1
点所处矩阵的列:
round((xi-x_min)/(range_x/round(range_x×k/min)))+1
点所处每个矩阵的体素数组下标即高度。
round((yi-y_min)/(range_y/round(range_y×k/min)))+1
为了防止计算结果越界,当三个参数大于约束的范围时,将对应值减一即可。
1.2.2确定点云凹陷体素集合
本文确定一个体素是否可能属于凹陷体的判断原理主要有以下两点:
(1)以y轴作为点云的高度轴,该体素包含点数少于阈值且低于所处对应xz平面grid区域上的最高点。
(2)该体素包含点数少于阈值并对于该体素做xz平面上的切面,在如图4所示的8个方向上向外延伸,存在4个及以上方向被非空体素所阻隔。
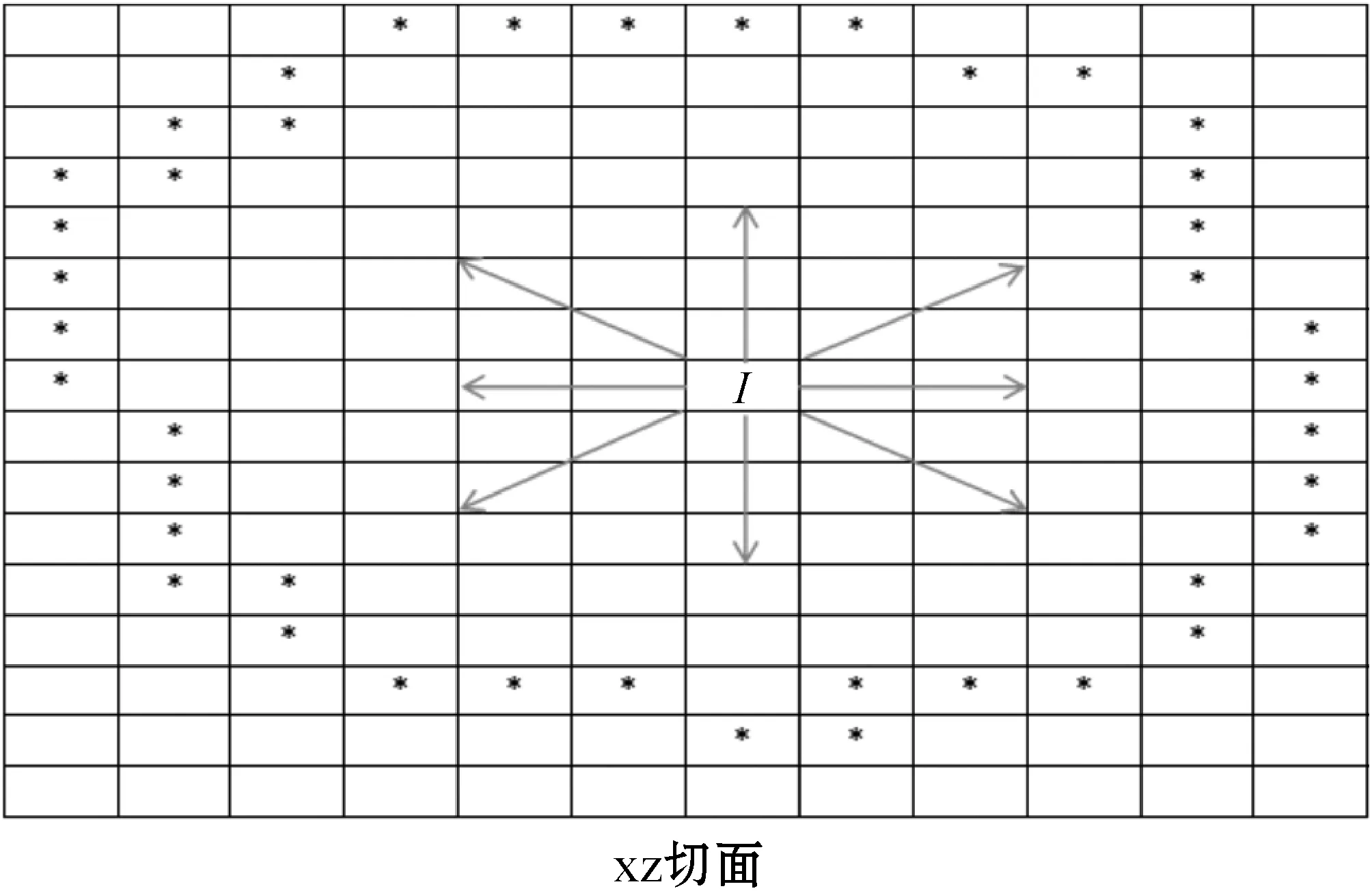
图4 体素判定原理图
图4为xz平面上的切面图,带*的方块表示label为-2即包含点数大于阈值的体素,不含任何标记的方块表示包含点数小于阈值的体素。
因此在遍历体素过程中,首先判断体素的label值,如果label值为0,判断其是否低于该平面区域上的最高点,若结果为true,放入凹陷判定集合Q;否则,对该体素在xz切面的8个方向上依次延伸,设当前正在进行处理的体素为I,如图4中带I标记的方块所示。以斜右上方方向为例,设体素I所处的空间中的行、列、高为I.row、I.col、I.height,依次判断(I.row+i,I.col+i,I.height)处的体素label值是否为-2即判断在延伸的过程中是否会碰到label为-2的体素,其中i为自然数。其他7个方向同理,若在4个及以上方向均满足条件,则放入集合Q。
按照上述判断原理进行判断,形成凹陷体判定集合Q进行下一步判定。
1.2.3凹陷体素集合分割与判定
对集合Q采取基于连通性原理的区域增长思想进行处理,设初始组数s=1,定义集合LK来存储各个凹陷体的体素。
(1)取出Q中未处理的体素,如果label为0,更改其label值为s并放入LK中。
(2)判断Q中是否存在与当前LK内体素相邻的元素,即在行、列、高三个方向上存在两者相等,另一个相差为1。若存在则将label修改为s,加入到LK中。
(3)按照第二步中规则继续处理新加入LK的体素直至找不到相邻的体素,清空LK,s++并重复第一步直到Q中所有体素均遍历完毕。
1.2.4凹陷体正确性判定
对于分割出的各个凹陷体,按照如下两种方式进行正确性判定:
1)凹陷体大小。有些判别结果所包含体素个数较小,表示这部分区域占模型的比例较小或者属于噪声区域,对结果的影响不大,因此本文通过定义组成凹陷体的体素个数与组成点云模型体积的体素个数的比值的一定比例作为阈值来筛选掉此类结果。
2)凹陷体连通性。经过该方法计算出的凹陷体中包含有模型内部的空洞,这是通过三维重建等方法获取点云的必然结果,因为点云中的点只分布于实体边界周围而实体内部没有点,因此按照本文算法,实体内部的区域也会被计算为凹陷体即假凹陷体。本文建立模型的外部附加层,以各个凹陷体与附加层的体素相邻的个数作为阈值进行判定。
1.2.5计算凹陷体边界
对于计算出的各个正确凹陷体,本文通过判断组成凹陷体的各个相邻体素判定其边界点。
对于组成凹陷体I的体素q,如果q在空间上的6个直接相邻体素中存在label为-2的体素,则该体素内的点即属于该凹陷的边界,通过遍历凹陷体的组成体素可以得到完整的边界点。依次对各个凹陷体进行同样处理可以得到对应的边界点集合。
2 实 验
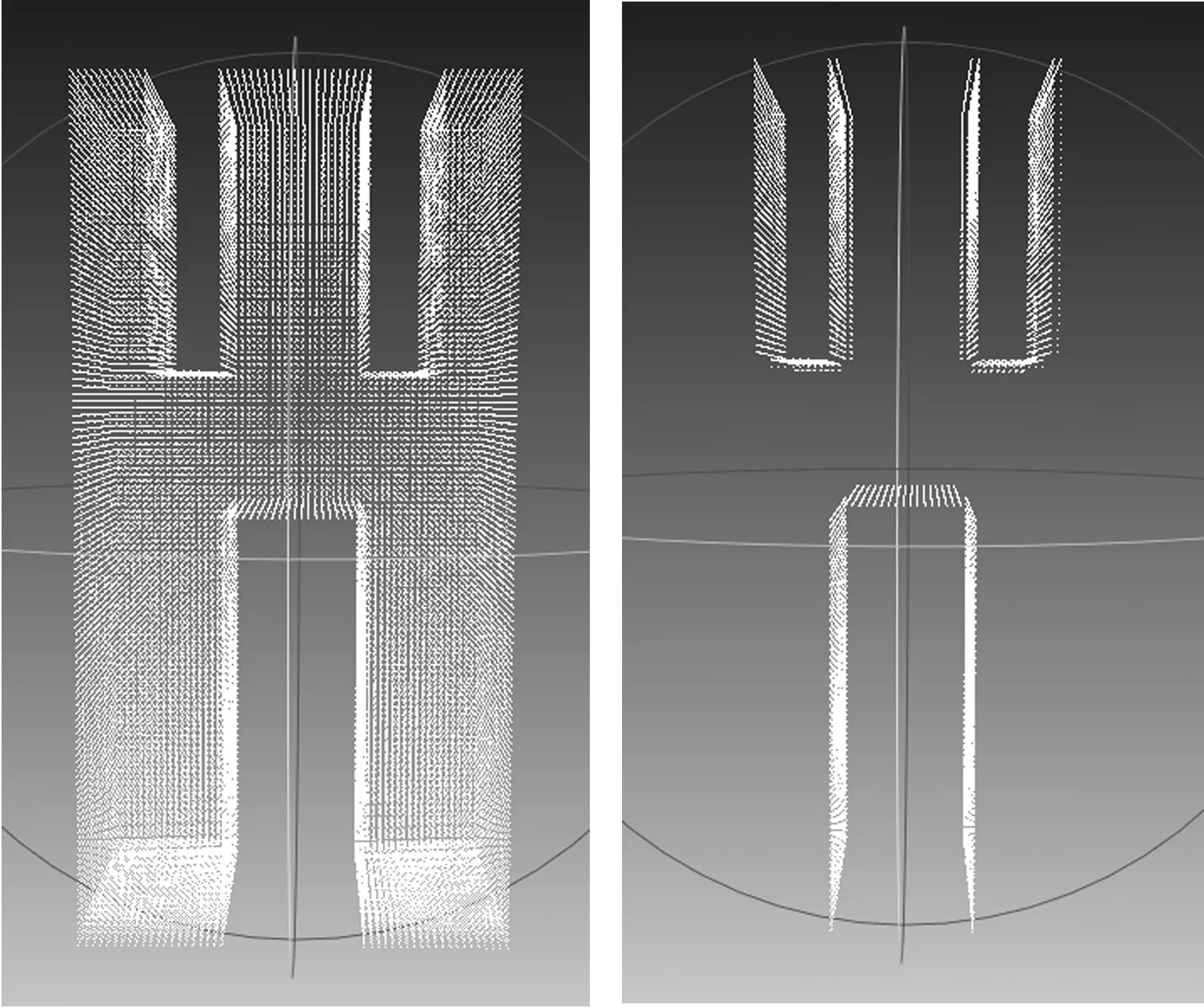
本文应用C++语言,借助visual studio 2013实现了上述算法。由于现有的研究中均是对点云数据边界或是孔洞边界的提取,缺乏对点云中凹陷体的判定研究,缺少相关的实验结果,无法进行对比。因此本文自行构建了两个带凹陷体的点云对算法进行测试。通过将点云文件分割成近60 000个体素得到的实验数据结果如图5、图6所示,本文借助Meshlab软件对处理的结果进行显示。图5(a)所示的实验数据中共包含三个凹陷体,图6(a)所示的实验数据中包含六个凹陷体,在图5(b)、图6(b)中均被正确地识别出来,实验结果中的点表示各个凹陷体的边界。点云数据内部的空洞由于不符合与外界连通的原则,则被排除。实验结果证明了本文算法的可行性,其可以稳定地判定出点云数据中的凹陷体。
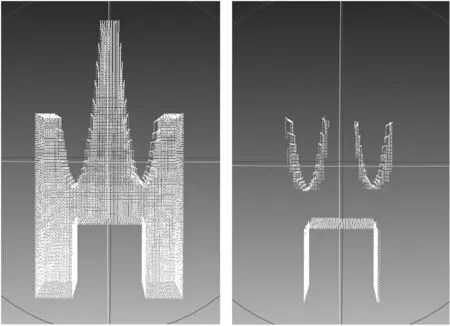
(a)实验数据 (b)实验结果图5 实验1

(a)实验数据
3 结 语
本文考虑到体三维显示系统无法正确显示带凹陷的点云数据问题,首先对凹陷体概念作了规范化定义,并根据凹陷体的属性特征提出了点云凹陷体判定算法PCDD,实验结果证明了算法的可行性。点云凹陷体能够应用于三维显示领域及CAD领域,体三维显示系统可以通过模拟透过凹陷体观察到的颜色来实现更真实的三维显示效果,CAD领域可以通过对凹陷体的精确把握实现高精度的模型设计,有很好的应用价值与发展前景。

