基于时间窗口聚类的时序数据索引压缩

刘 璐 王 鹏 汪 卫

1(复旦大学软件学院 上海 200120) 2(复旦大学计算机科学与技术学院 上海 200120)

0 引 言

随着智能设备的大量应用，在很多应用场景中会生成大型的数据集，如用户登录数据、设备运行状态数据等。这些数据在不同的时间段上会表现出不同的特征。在对数据进行挖掘的过程中，常需要去发现属于特定时间段的相似数据序列。以下的一个例子可以说明多时间段上相似性查询的问题。图1给出了一个收集了不同区域的降雨情况的数据集，横坐标代表时间戳，纵坐标代表具体的降雨量的数值。考虑这样一个问题：找出在特定时段(例如t1到t2时间段)内与上海表现最相似降雨趋势的区域。在这个问题中，查询的时间段是固定的。一种直接的查询方式就是通过遍历整个数据集中t1到t2时间段内的子序列来寻找最近邻。但是当数据量很大时，直接从数据集中读取全部的序列并进行序列相似性计算是很费时的。为了加快查询过程，可以给t1到t2时间段内的子序列建立索引。每一段子序列被表示成一个摘要的值，然后根据这些摘要来建立索引。数据序列的摘要可以近似序列之间的距离，从而剪枝掉不必要的时间序列。上述的过程是在固定的时间段上创建索引来支持该时间段上的查询。

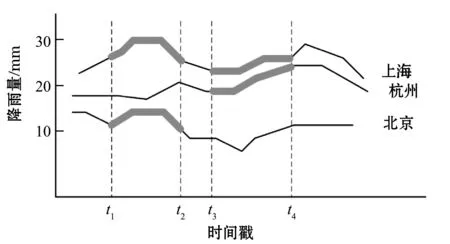
图1 多个地区降雨量

构建单个索引以支持限制在该窗口上的查询是可行的。但是，当查询窗口更改为(t3,t4)时，又需要构建一个新索引。以图1中的数据为例，时间序列在不同的时间段上是变化的。在时间段(t1,t2)中，北京的降雨量与上海的更为相似，但在时间段(t3,t4)内,答案应该是杭州与上海更相似。因此，需要建立不同的索引来满足不同的查询窗口。显然，如果要支持大量的查询窗口，建立索引需要消耗的时间和空间将是巨大的。例如，对于包含长度为104个时间戳的序列的数据集，可能窗口的数量约为108的数量级(考虑全部可能的时间窗口)。

目前的问题是，一些对时序数据建索引的方法只能为单个时间段(序列的一部分或整个序列)构建索引。换句话说，对于可变窗口的查询，这些方法需要在实际查询每个窗口上的子序列之前为该窗口建立索引。很明显，这既费时又费空间。另一方面，一些已有的可变长度索引对基于窗口的查询执行表现出较低的查询效率。因为当查询受窗口而不是长度限制时，它们的剪枝策略效率低下。本文提出一种构造轻量索引的方法，达到较低的总索引代价，对于可变窗口具有高的查询执行性能。本文方法可以支持精确和近似最近邻(NN)查询以及范围查询。

1 关键概念

(1)时间窗口：如图1所示，横坐标t1到t2这一段时间就称为一个时间窗口。

(2)时序数据子序列：数据序列T={p1,p2,…,pn}是长度为n的序列，其中每个数据点pi按时间戳的顺序出现。数据序列在窗口w上的子序列表示为Tw，其中窗口w通常表示为(s,e)，其中s和e定义时间窗口w的开始时间点和结束时间点。

(3)时间窗口的集合：时间窗口的集合可以表示为WS={w1,w2,…,wm}。集合中的每个窗口由一个开始时间戳s和结束时间戳e表示出来。

(4)带有窗口限制的N近邻查询：给定一个时间序列的集合D,给出一条查询序列Q和一个查询窗口w(s,e)，用规范化的欧氏距离来衡量时间序列之间的距离。查询N近邻的含义是：从所有限制在时间窗口w(s,e)的子序列中找到与查询序列Qw距离最近的N条子序列。

(5)带有窗口限制和阈值范围的查询：给定一个时间序列的集合D,给出一条查询序列Q和一个查询窗口w(s,e)以及距离阈值ε。范围查询的含义是：从所有限制在时间窗口w(s,e)的子序列中找到与查询序列Q距离不大于阈值ε的所有子序列。

2 相关工作

对于时间序列距离的衡量，目前已经有很多文献提出距离计算的方法。给定两个标准化的时间序列Q和T，一个相似的函数dist测量Q和T之间的距离，用dist(Q,T)表示两条序列之间的距离。目前主要的序列距离计算方式包括欧氏距离(ED)[1]、DTW[2]、最长公共子序列(LCSS)[3]等。在这项工作中，使用ED作为距离测量。ED是时间序列中最常见的相似性度量，因为它很简单且便于计算。对于距离测量的详细信息，可以参考文献[4]。

为计算在某个窗口上的相似子序列，直接扫描所有子序列进行查询非常耗时。之前很多工作提出了许多计算序列摘要方法，使用子序列的摘要值对子序列进行剪枝，例如：离散傅里叶变换[5]、奇异值分解、哈尔变换[6]、APCA[7]、分段均值(PAA)[8]和SAX[9]等。在不同的应用中通常需要根据剪枝的能力对摘要进行选择。

为了加快查询速度，现有方法通常会根据序列的摘要创建索引。索引构建方法可分为两种样式：自顶向下索引和自底向上索引。自顶向下的方式构造索引会从根节点开始把序列放到节点中[10-12]，当节点容量满了之后就将节点进行拆分。这种方法会导致许多小的随机I/O存储，从而降低索引构建速度。同时，由于节点大小不固定，整个指数结构是较难描述的。另一种自底向上的构造索引方式，例如Coconut[13]，在索引构建之前对数据序列进行排序，从而避免存储空间的再次分配。因此，它以更快的方式构建索引，而无须拆分节点。一旦序列被排好序，序列的摘要和序列指针就会直接被刷新到磁盘。

除了单独对每个时间窗口建立索引，目前有一些把多个窗口的索引压缩到一起的方法[14-16]。但是这些索引压缩的方法对基于窗口的查询表现出较低剪枝能力，因为这些索引压缩的方式没有充分考虑到索引的特征和相似程度，导致压缩后的索引比较粗糙。另一方面，这些方法通常只是把邻近的窗口上的索引压缩到一起，而并不能把非相邻窗口的索引进行压缩。

总之，不管是单窗口的索引还是已有的可变窗口的索引，都不能有效地用于基于窗口的相似性搜索问题。这项工作提出了利用不同查询窗口的索引的相似性，对索引的时间空间开销进行优化。

3 方法描述

3.1 方法目标和方法概述

对于查询窗口较多的时候，为每个时间窗口分别建立索引是很低效的方式。对于所有需要建立索引的时间窗口，本文的基本思想是，如果两个窗口上构建的索引具有类似的索引结构，则这两个窗口的索引是相似的。通过把相似的窗口聚类到一起，提取出相似的索引中冗余的部分，以达到索引压缩的效果。

3.2 窗口索引的相似度

这里主要考虑对于自底向上索引结构的压缩。正如前文讲到过的，自底向上的索引结构通常根据时间序列排序的情况来组织序列，基于排序来构建索引。也就是说，窗口上时间序列的排序情况决定了窗口的索引结构。这一特征有助于比较不同索引之间的相似程度。

序列和窗口之间的关系可以由图2体现出来。对于图2中的4个窗口w1-w4,12条序列T1-T12，每一条序列都可以在4个窗口上切出4条不同的子序列。每段子序列可以计算出一个摘要值(例如摘要可以定义为一段子序列中数据的均值)。由于在不同的窗口上计算出的摘要值不同，子序列的排序情况不同，从而不同窗口的索引结构就不同。在实现方法的时候，本文使用的序列排序方式参考文献[13]。

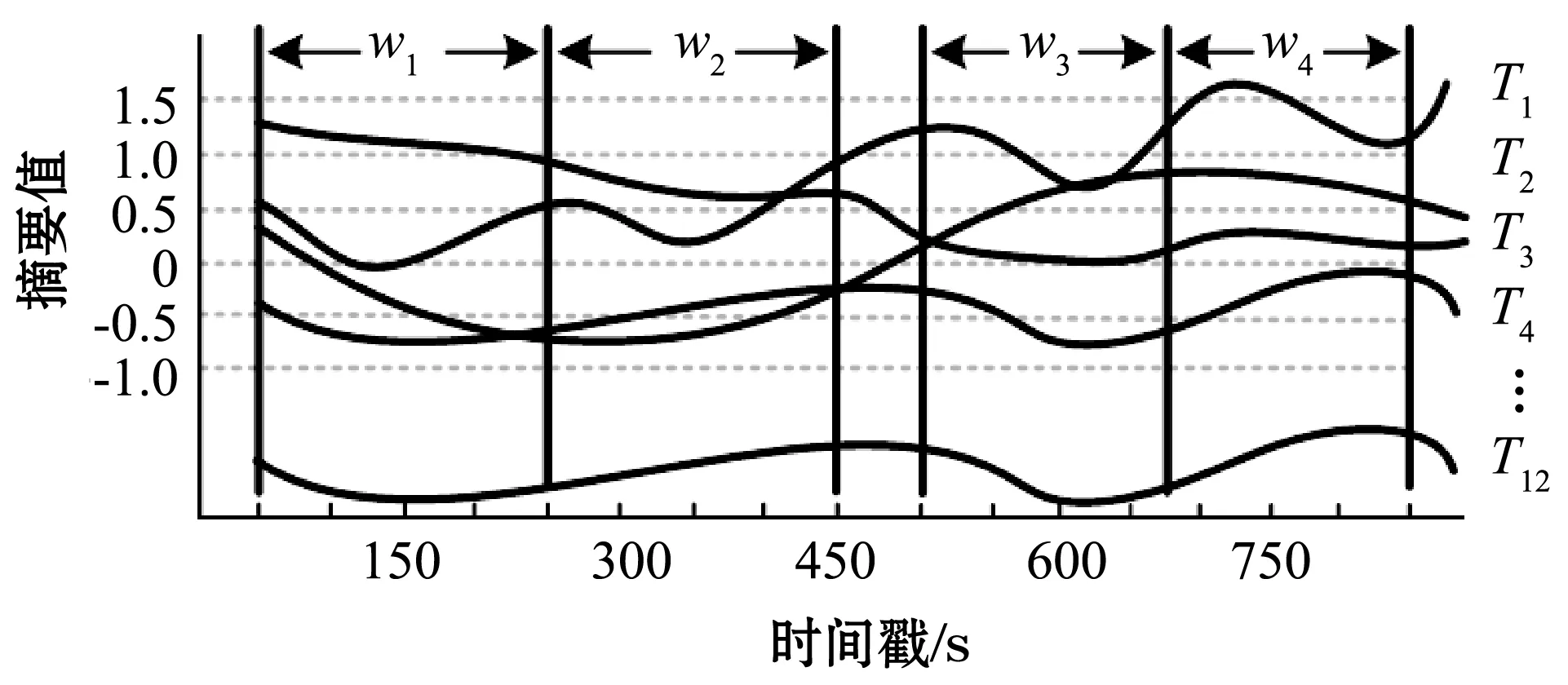
图2 不同窗口上序列的相对位置

下面说明如何根据窗口内序列排序的情况来计算窗口间的距离。这里举例了两个窗口w5和w6。表1中序列的顺序就是子序列的两个窗口上的排序情况，w5和w6上序列顺序略有不同。直接拿排序情况比较两个窗口的相似度复杂度会较高。事实上需要比较的是两个窗口上每个排序区间包含的序列的差异。

表1中列举了一个简单的例子。把排序后的12条序列划分成3个长度为4的排序区间：1～4、5～8、9～12。对w5和w6两个窗口而言，每个窗口上的12条子序列分别放到了如表1的排序区间里。那么通过比较每个排序区间，就能比较出两个窗口的差异。

表1 不同窗口上的排序情况

对表1两个窗口的表示，并不能直观地进行计算。为了数字化地表示出每个排序范围里分布了哪些子序列，本文把序列按照它们的编号又进行了分组。若设置编号分组大小为3，那么编号为前3的序列依次为T1、T2、T3就被分到第一个编号分组，T4、T5、T6属于第二个编号分组，以此类推第三编号分组中的序列是T7、T8、T9，第四个编号分组是T10、T11、T12。然后就可以通过计数的方式表示序列的分布情况。如表2所示，把每个排序区间都总结成4个数值(这里数值的个数等于编号分组的数量)，这4个数值分别表示各个编号分组内的序列有多少个出现在了当前的排序区间。例如，w5中的排序1～4的序列中有3个序列属于第一个编号分组，分别为T1、T2、T3，而T4属于第二个编号分组。第三和第四个编号分组的序列没有出现在排序区间1～4中，所以计数分别为3、1、0、0。w5中排序为5到8的序列中没有第一个编号分组中的序列，有2个(T5和T6)属于第二个编号分组的序列，第三个编号分组的序列(T7)和第四个编号分组的序列(T11)各有一个，所以计数分别为0、2、1、1。w6的序列分布情况计算是同理的。这样就统计出了各个窗口上序列的分布情况。可以看到虽然w5和w6的序列排序不完全相同，但是表示出来的序列分布情况是相同的。这就意味着本文方法根据索引结构的实际情况比较索引之间的相似程度，而不是仅仅依赖于精确的序列排序，这样的计算方法更有利于找到相似的索引，并且计算复杂度也相对低。

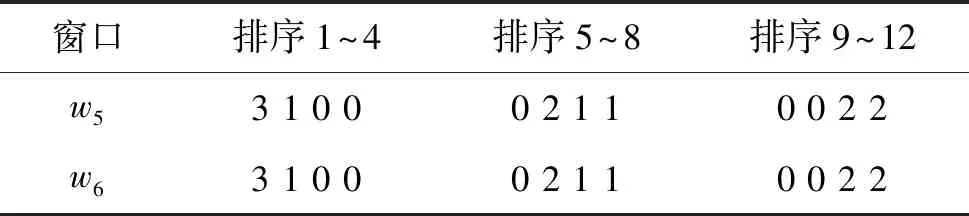
表2 窗口的表示

把窗口的每个排序区间的表示拼起来表示成一个向量，例如w5表示为<3,1,0,0,0,2,1,1,0,0,2,2>。进而，窗口间的距离就可以用窗口间的欧氏距离来计算。

3.3 窗口聚类

将每个窗口表示成了上述的向量形式，然后用向量间的欧氏距离来度量不同窗口的索引间的距离，根据这个距离来对窗口进行聚类。基于以上的窗口向量和窗口距离定义，本文使用k-means[17]对窗口进行聚类。参数k用来控制聚类的个数。聚类过程首先选择k个窗口的向量作为初始k个聚类中心：

(1)聚类更新：给每个窗口计算它的向量到k个中心向量的欧氏距离，把每个窗口分到距离最近的那个聚类。

(2)重新计算聚类中心：对更新之后的每个聚类中所有向量计算，计算这些向量的均值作为新的聚类中心。

这样就得到了k个窗口的聚类结果。接下来的建立索引的过程是逐一在这k个聚类上分别进行的。

3.4 索引结构和构建方法

对于每个窗口的聚类，只选择一个代表窗口，同一聚类中的其他窗口被称作附属窗口。本文选择离聚类中心最近的窗口作为代表窗口。下面分别介绍如何为代表窗口和附属窗口创建轻量级索引。

(1)代表窗口：代表窗口索引的构建遵循常规的自底向上构建索引的方式，首先对数据集中的所有时间序列切分出代表窗口内的子序列，然后对子序列进行排序[13]。指定索引中节点大小的参数，把排好序的序列依次放到节点中，当第一个节点装满后，就继续装第二个节点，以此类推。同时每个节点维护一个摘要用来描述节点中包含的时间序列的信息。每个节点的摘要就作为最终该节点的索引信息。

(2)附属窗口：在构造索引的步骤中，附属窗口内的子序列不需要再进行排序，而是使用该窗口所在聚类的代表窗口同样的序列排序。也就是说附属窗口的每个节点指向的序列集合与它所在聚类的代表窗口相同。附属窗口同样需要计算每个节点的摘要，作为描述节点的索引。由于窗口是不同的，节点的摘要计算出来也是不同的。

也就是说，每个聚类中只维护一次序列的排序情况，而不是给每个窗口都维护依次排序。由于只维护代表窗口的排序，这样很大程度上节省了索引占用的开销。这个聚类中唯一维护的排序称为聚类的排序。每个聚类的排序和聚类里所有窗口的对应关系如图3所示。聚类C1中只包含了一份排序信息，聚类中的两个窗口依次根据每个排序区间的序列构建节点的摘要。每个窗口的节点摘要和排序的对应关系如图3所示。

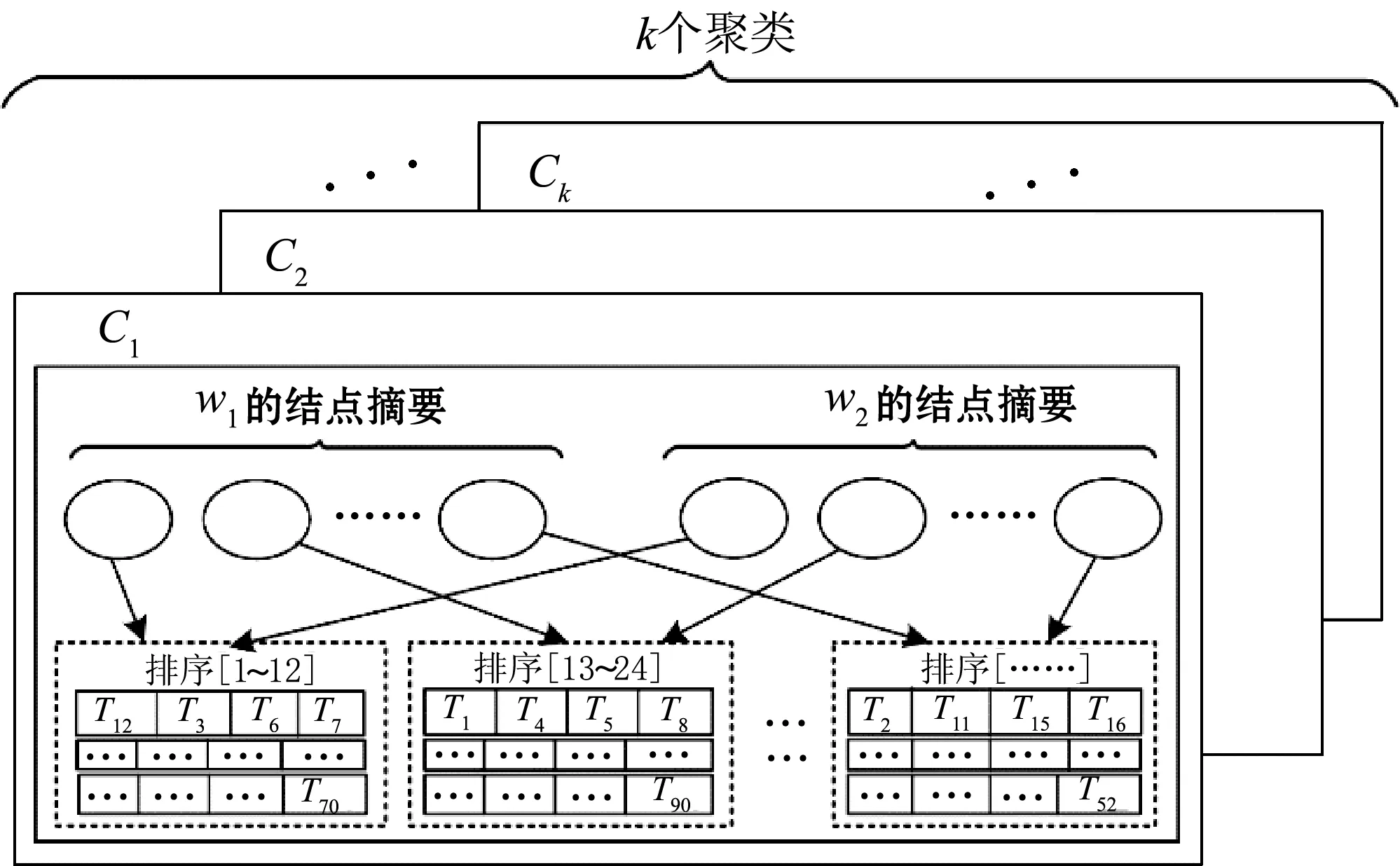
图3 索引结构图

(3)节点摘要的计算：无论是代表窗口还是附属窗口，每个节点的摘要其实总结了该节点指向的所有子序列。由于排序中只保留了序列的编号，在计算不同窗口上的节点摘要的时候，只需要把序列对应到不同窗口上的子序列然后计算即可。节点摘要可以用来计算任意一条查询序列到节点指向的全部序列的距离下界。

例如，给定一个序列子集S={T1,T2,T3,T4}，每个子序列可以表示成x段的SAX值[5]，这里举例x=3。那么指向子集S的节点摘要就由两个长度为3的下界和上界构成。下界用向量L来表示，上界由向量U来表示。另外，用SAXi(Tj)来表示序列Tj的SAX值的第i段，其中：i=1,2,3；j=1,2,3,4。那么L和U可以描述为：

式中:参数i表示L和U的第i个分段。有了这样的节点摘要，就可以明确计算出任意一条查询序列到一个节点指向的全部序列的距离下界，这样就能保证在查询的过程中不去访问那些一定不包含最终结果的序列。文献[16]给出了定理来说明如何计算这个距离下界。

4 基于索引的查询

本文的索引支持以下三种查询：近似N近邻查询、精确N近邻查询和带阈值范围的查询。对于一个查询Q和窗口w，Q到一个节点中所有序列的下界距离可以由公式计算出来，参考文献[16]。

4.1 近似N近邻查询

经典的基于索引的查询方式[13]在计算近似解的时候，通常优先访问最有可能包含结果的节点。类似地，CBI选择Q和节点的摘要之间下边距离最小的节点摘要。锁定节点摘要之后，可以定位到摘要指向的一段排序中包含的所有序列，然后计算Q到这些序列的确切欧氏距离，选出距离最小的N条就完成近似N近邻的查询。

4.2 精确N近邻查询

在精确N近邻查询中，首先使用近似查询的答案作为初始的最优解(BSF)。然后用BSF来检查查询窗口w的每个节点摘要。对于距离下界大于BSF的节点摘要可以直接剪枝掉，不再继续访问该节点中的序列。对于满足距离下界的节点摘要，定位到该摘要指向的一段排序中的全部序列，逐一计算Q到节点中每条序列的距离，并更新最优距离。完成对所有节点摘要的检查后，就得到了精确N近邻查询的解。

4.3 带阈值限制的查询

由于每个节点都维护了一个可以提供距离下界的摘要，当查询带有阈值限制时，直接检查每个节点摘要和Q的距离下界，如果节点摘要的距离大于阈值，则不再继续访问当前节点指向的序列。反之，如果当前节点的距离下界小于阈值要求，则逐条检查节点指向序列和查询Q的精确欧氏距离是否满足阈值，满足阈值的序列即加入到结果集合中。

5 实验与结果分析

5.1 实验设置

所有实验均在16 GB DDR4内存的Intel i7-7700k CPU上执行。本文测试了以下数据集：

(1)真实数据集使用的是一个湿度数据集，其中包含1998年1月至2018年12月从美国9 115个不同站点收集的湿度测量数据[18]。该数据集的总大小为8 GB，包含约2×109个浮点数，数值范围为[0,100]。

(2)生成数据集合成时间序列是由随机游走时间序列、高斯时间序列和混合正弦时间序列三种时间序列组合而成的。生成一个4 GB的合成数据，其中包含10万个数据序列，长度为10 000，数据数值范围为[-5,5]。

本文实验的所有方法都是使用Java语言实现的。

5.2 索引的性能

为了评估CBI创建索引的性能，进行了聚类效率的研究。如图4所示，3 200个聚类过程需要大约30 min。聚类几乎是CBI中唯一耗时的过程。这说明CBI建立索引所需要的时间开销较小。

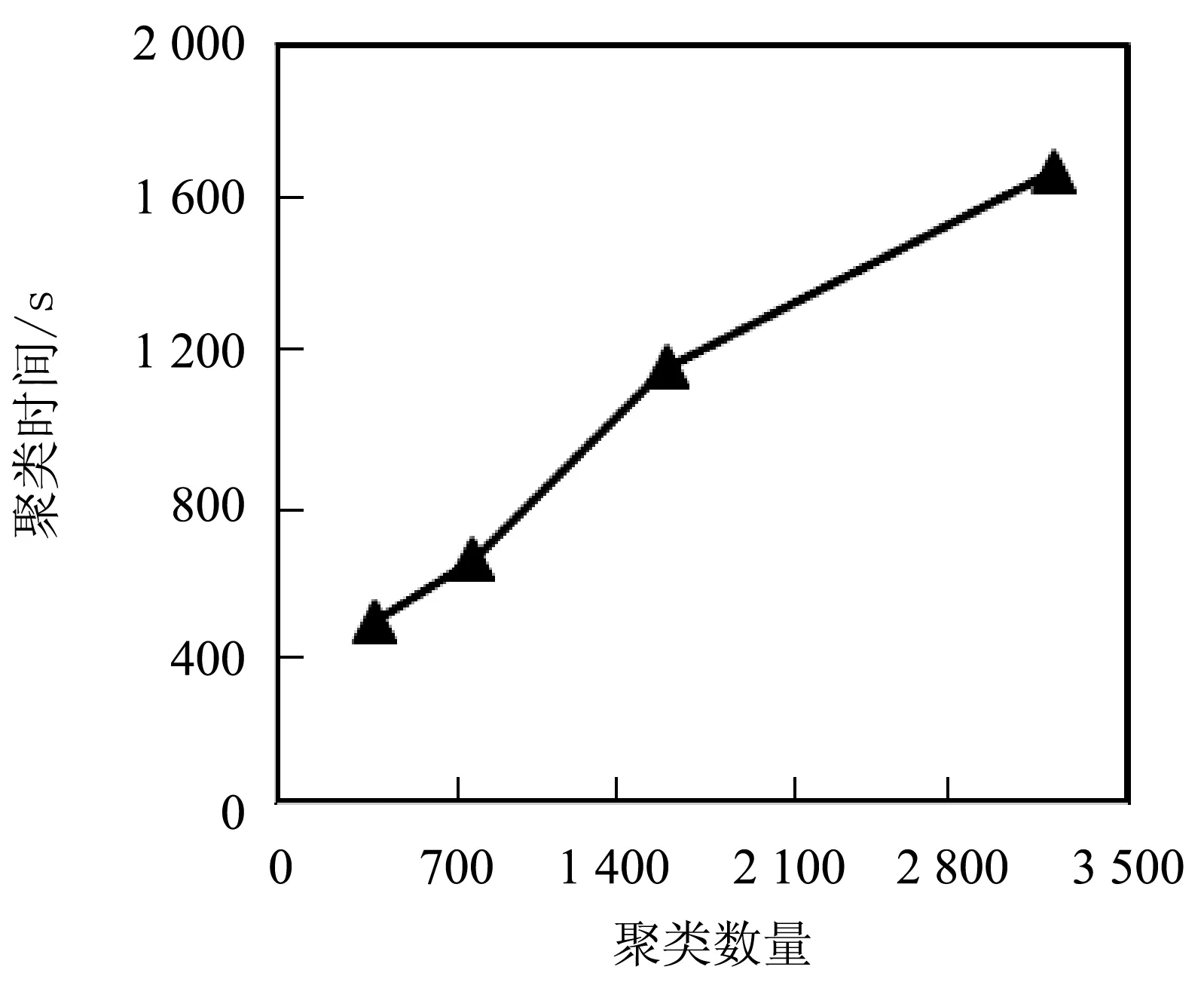
图4 CBI聚类时间

图5显示了CBI在多个窗口的索引建立方面如何优于Coconut方法。从平均每个索引建立的时间开销来看，本文的索引在基于窗口的索引时间上是优于普通的单索引构造方式的。

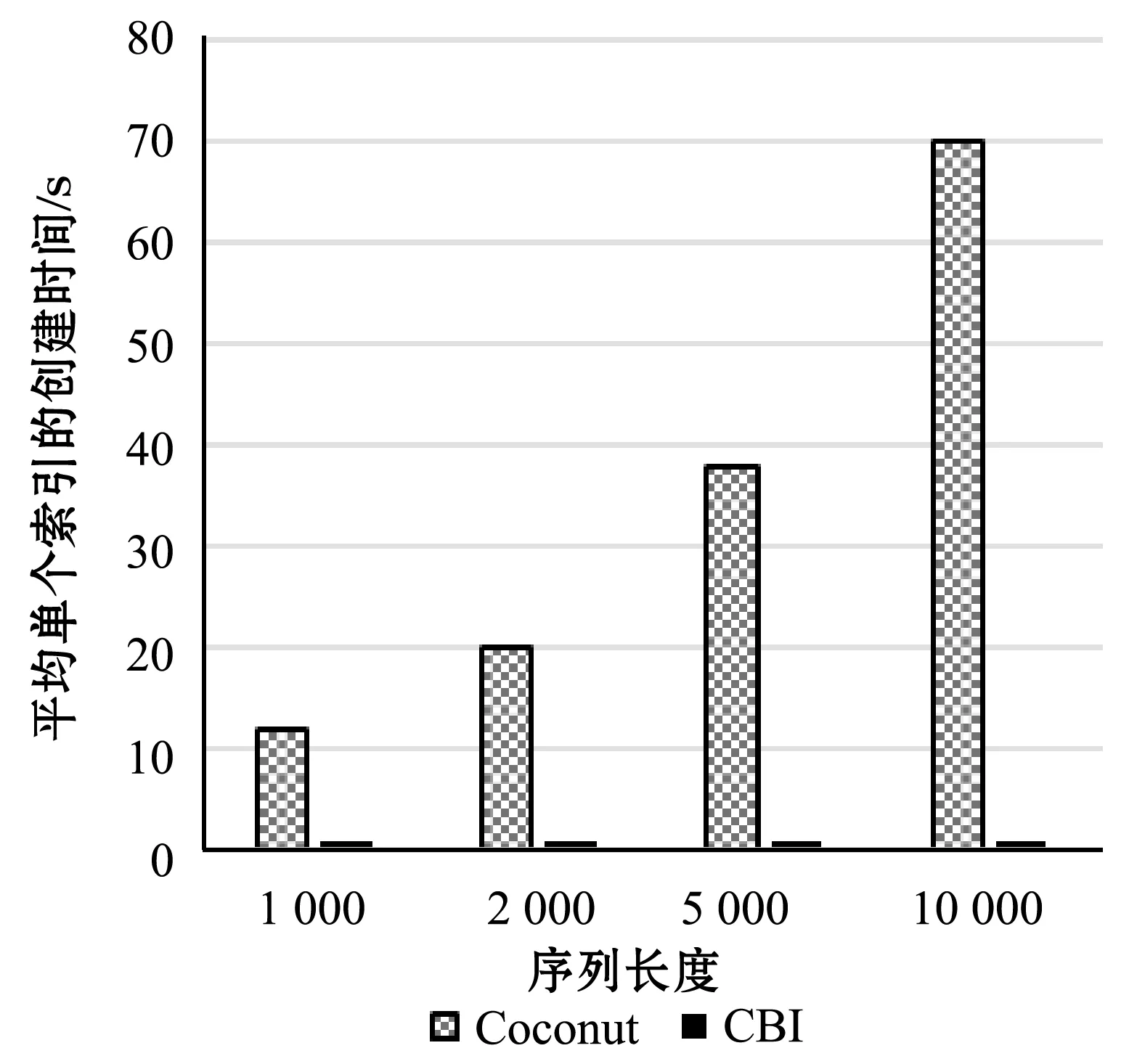
图5 平均每个窗口上索引的构造时间

空间使用分析：当索引参数固定时，CBI和Coconut消耗空间大小分别都是固定的。以4 GB的生成数据集为例，假设每个序列由16段的SAX表示，索引的节点大小设置为200，单个窗口的Coconut索引的最终大小为7 MB。CBI单个压缩索引的大小为32 KB。很明显，CBI索引大小比Coconut小得多。需要构建的基于窗口的索引越多，CBI节省的空间就越多。

5.3 查询性能

通过与Coconut索引和子序列匹配方法KV-match[19]进行比较，评估CBI的查询性能。由于这两个对比算法本身的原因，它们并不完全支持文中列出的这三种查询。Coconut支持精确和近似的N近邻查询，KV-match支持阈值范围查询。

(1)N近邻查询：比较了CBI与Coconut的剪枝效率，在生成数据集上选择查询窗口长度为1 000的整数倍，并对每个窗口运行10个随机查询。平均剪枝效率如图6所示，图中的数据比较了不同聚类情况下CBI的效率，横坐标CBI括号里的数字代表聚类个数。剪枝率定义为查询过程中从磁盘上读取的序列的数量比上总的序列数。6 400个聚类的CBI的剪枝率为91%，略低于Coconut的93.6%。对于CBI，构建的聚类数越多，剪枝效率越高。

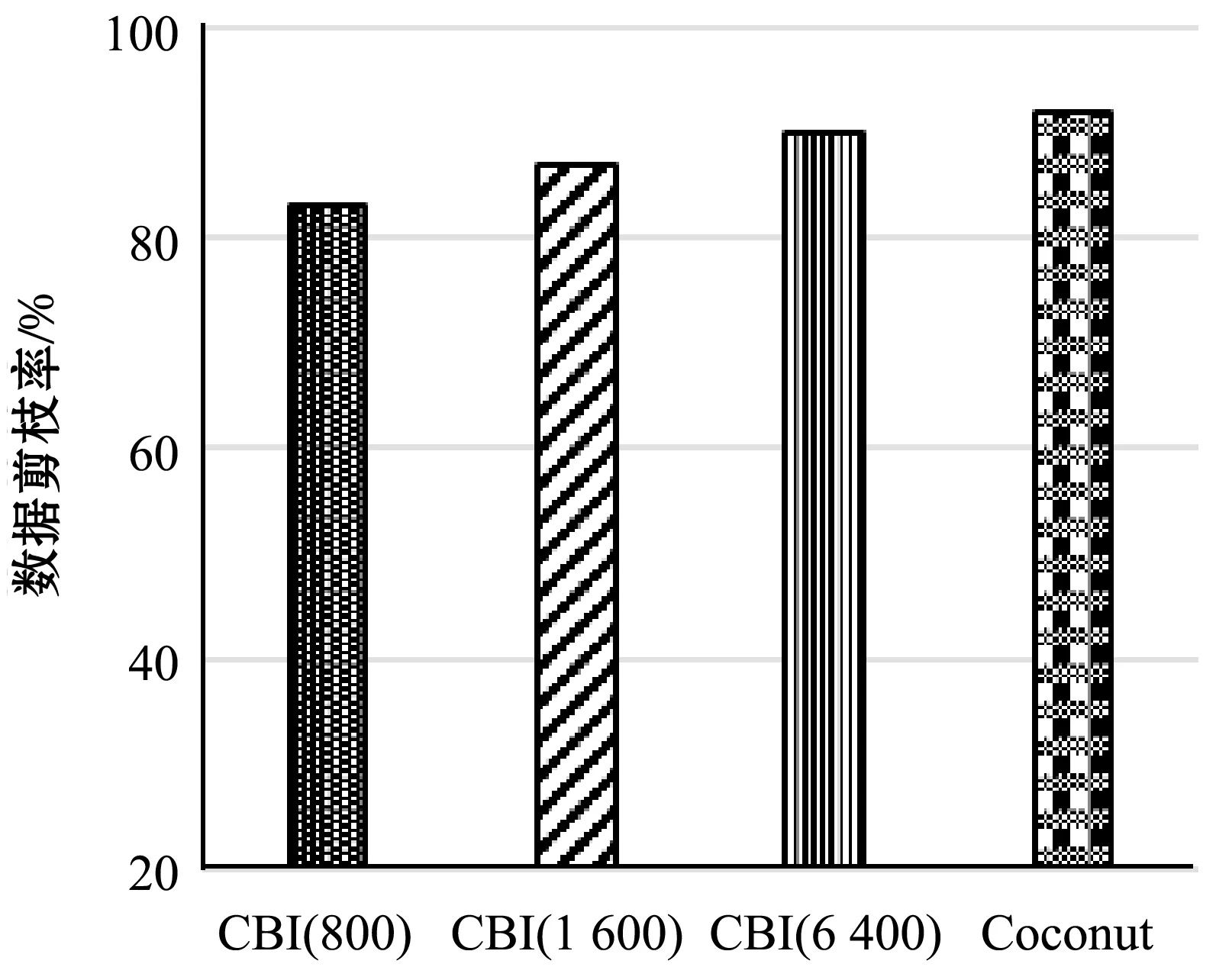
图6 剪枝率

查询时间如图7所示。随机选择长度为1 000的窗口，将查询时间与Coconut进行比较。除了CBI和Coconut之外，还对比了直接暴力搜索的方法运行查询的时间开销，该方法直接扫描磁盘上的数据集并计算查询与所有数据系列之间的标准化欧氏距离。结论是，CBI在节省空间开销的同时，可以很好地保证查询效率，平衡了直接搜索的查询方式和单索引Coconut的不足。

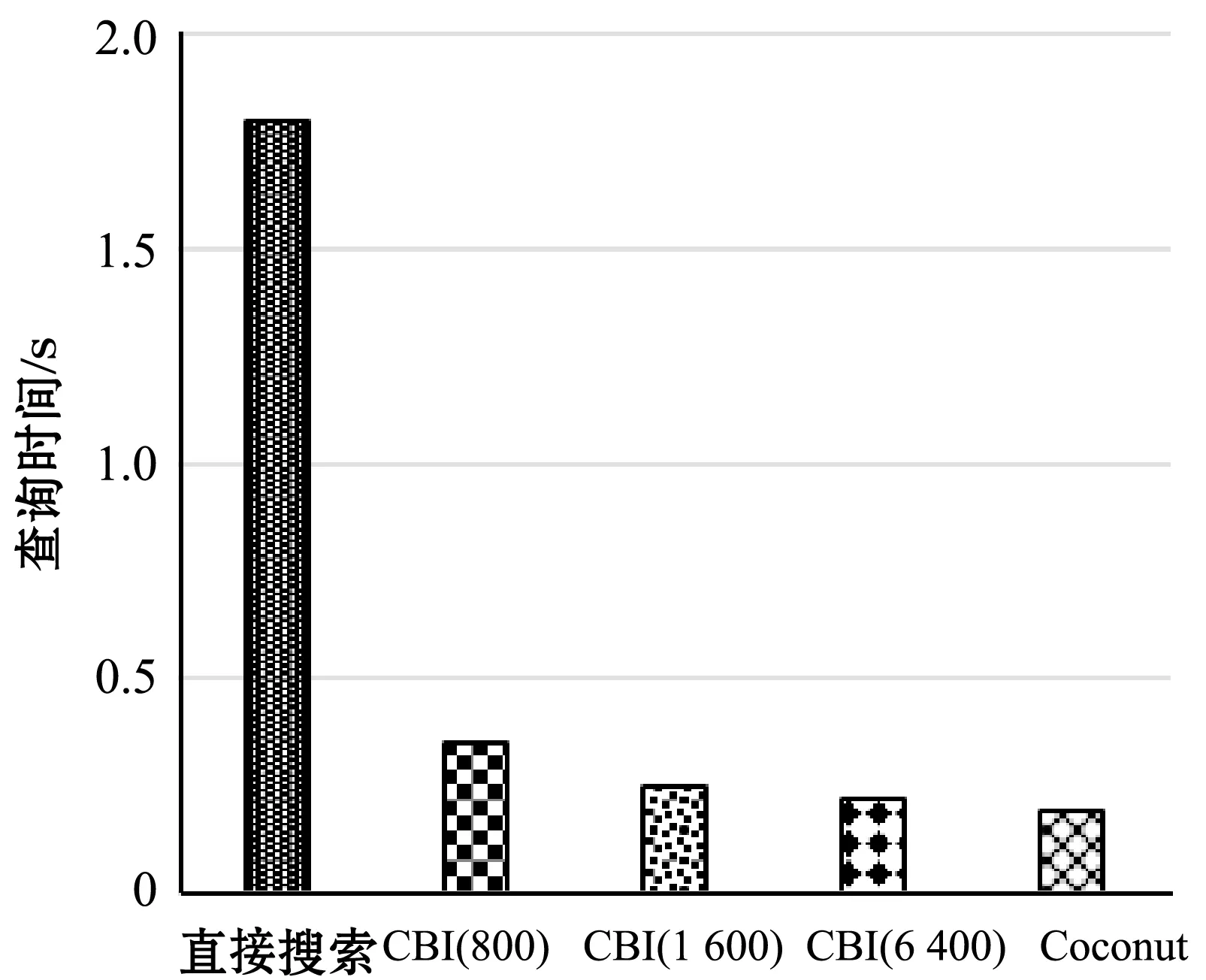
图7 不同方法的查询时间

(2)带阈值限制的范围查询：由于Coconut索引的结构不能支持阈值限制查询，通过选择可变长度的索引KV-match来验证CBI的阈值查询性能。在生成的数据集上测试了各种范围阈值，并使用1 000的查询窗口长度。图8给出了KV-match在变量窗口查询上执行的剪枝效率很弱。即使对于一个小的阈值3，KV-match也需要计算64 846个数据序列的精确欧氏距离，导致剪枝能力低于36%。CBI在范围查询中表现出较好的剪枝效率。

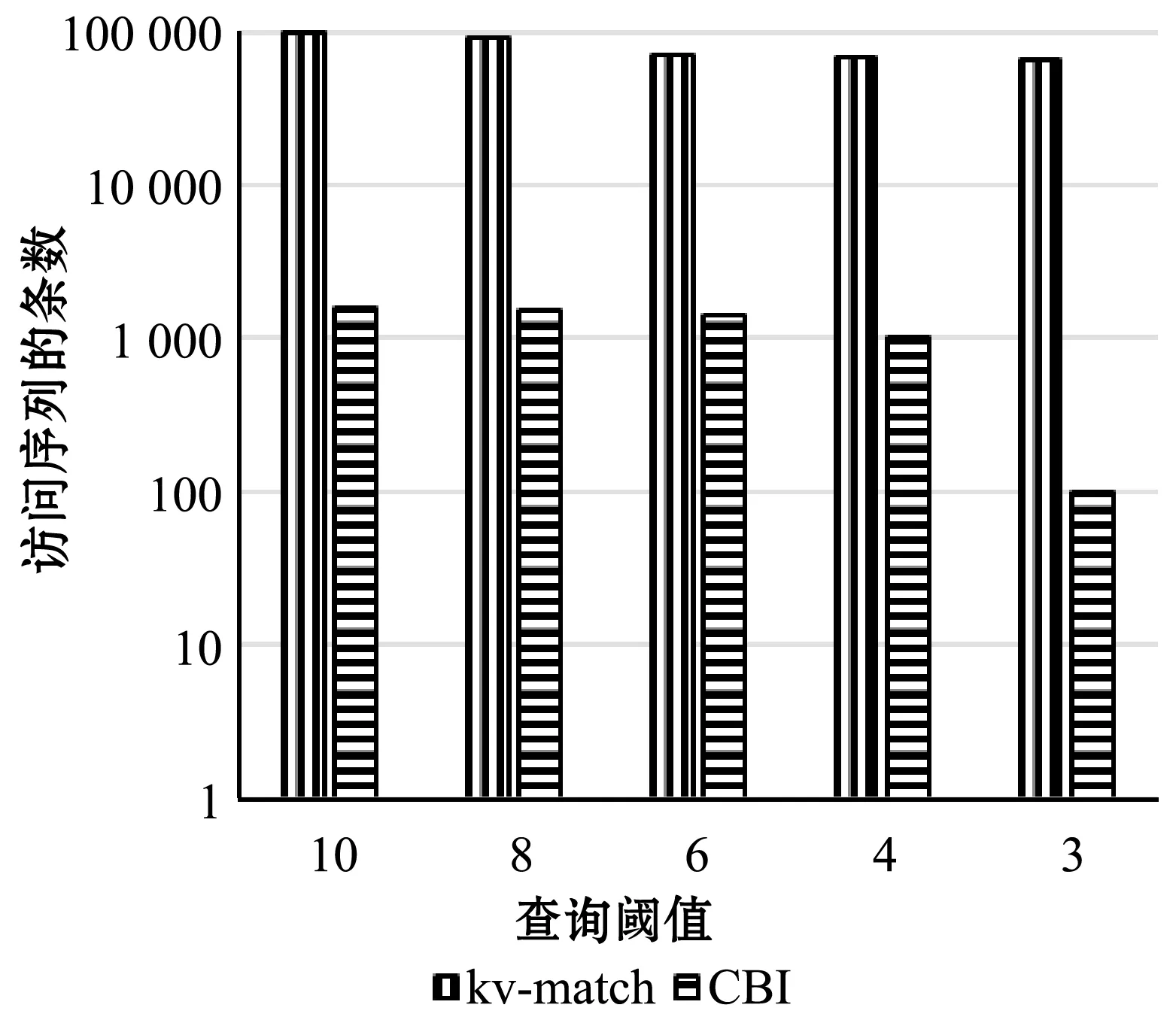
图8 不同阈值下的剪枝效率

6 结 语

本文论述了目前其他一些方法的索引不适合可变窗口查询的问题，提出一种压缩的自底向上索引(CBI)方法。本文从索引的原理、索引结构、索引构造方法等多个方面对提出的方法进行了阐述。实验结果表明，CBI能够高效、准确地回答给定数据集上的基于窗口的查询，比目前已有的方法在索引开销和查询效率方面有较大的改进。下一步将考虑如何进一步压缩CBI索引，进一步减少索引开销并继续提升索引查询效率。