基于正则互表示的无监督特征选择方法

汪志远，降爱莲，奥斯曼·穆罕默德

（太原理工大学信息与计算机学院，山西晋中 030600）

（*通信作者电子邮箱ailianjiang@126.com）

0 引言

各种智能电子设备和信息系统的广泛使用产生和收集了大量的高维无标签数据。利用相应的机器学习算法对这些数据进行处理和分析，可以发掘数据的潜在价值。在模式识别与机器学习研究领域中，对于机器学习算法而言，样本数据集是训练模型的重要前提，但是收集到的原始数据通常含有大量的冗余特征，导致其并不适合直接被使用。冗余特征不必要地增加了数据的维数，降低了训练性能［1］。如果不剔除数据中的冗余特征，将会导致机器学习模型的训练时间变长，训练后得到的预测模型泛化能力差，甚至因遭遇维数灾难而使训练无法进行。文献［2］表明，去除冗余特征可以明显地提升训练效率。

特征选择是一种有效的数据降维方法［3］，它可以选出数据中的重要特征，剔除不重要的冗余特征，从而得到更加低维的数据。数据维数降低，可以减少机器学习模型的训练时间，提高模型训练效率［4］。根据学习任务类型的不同，特征选择方法分为有监督特征选择方法和无监督特征选择方法两大类［5］。有监督特征选择方法依据特征与标签之间的相关性来选出重要的特征子集，因为重要特征与标签之间的相关性更强。然而，并非所有的数据集都带有类别标签信息，数据无标签使得有监督特征选择方法不再适用，也使得特征选择变得更加困难［6-7］。

较早提出的无监督特征选择方法，如最小化方差法［8］和Trace Ratio 方法［9］，这些方法单独计算每个特征的分数，按分数排名选出特征，此类方法评价标准单一，对数据的解释能力较差。之后发展出基于谱分析技术［10］的无监督特征选择方法，此类方法通过对邻接图拉普拉斯矩阵进行谱分解，利用关联矩阵的特征值度量各个特征的重要性，但是该方法在处理高维数据时面临计算量过大的问题。目前，正则回归也被应用到特征选择，Zheng 等［11］提出的自步正则化无监督特征选择方法（Unsupervised Feature Selection by Self-Paced Learning Regularization，UFS_SP）和刘艳芳等［12］提出的邻域保持学习特征选择方法（Neighborhood Preserving Learning Feature Selection，NPLFS）将特征选择问题建模为损失函数最小化问题，对权重矩阵施加正则约束，表现出较好的鲁棒性，但是现有的正则特征选择方法优化困难，计算复杂度较高。

正则自表示（Regularized Self-Representation，RSR）方法［13］首次提出特征自表示性质，即高维数据的每个特征可由全部特征线性近似表示，该性质考虑了特征间的相关性，具有较强的数据解释能力，但该理论也存在不足之处，在目标函数优化时，特征权重容易向自身倾斜，导致无法合理地为特征分配权重。其他的基于自表示性质的特征选择方法均无法避免自表示性质的缺陷。为此，本文提出特征互表示性质，即高维数据中的每个特征可由除该特征之外的其他特征线性近似表示，而不是由全体特征线性近似表示，这克服了特征权重容易向自身倾斜的缺点。然后，基于特征互表示性质，提出一种新的正则化无监督特征选择方法，该方法能够有效提升数据聚类准确率，降低数据冗余率，并且计算复杂度较低。

1 特征互表示性质

假定X是数据矩阵，X∈Rm×n，m是样本数量，n是特征数量，fi代表X的第i个特征，则X可以表示为特征的集合：X={f1，f2，…，fn}。

高维数据中的每个特征可以由数据中的其他特征线性近似表示，特征之间存在相关性，因此可以很好地互相近似表示，把高维数据所满足的这一数学性质称为特征互表示性质。利用特征互表示性质，数据矩阵X中的每一个特征fi可形式化表示为：

式中：wj是第j个特征的权重系数；ei为残差向量，代表特征fi重构前后的残差。本文期望重构后的特征可以很好地近似表示原特征，所以残差应当尽可能小，使用向量的l2-范数的平方度量残差大小，将损失函数定义为：

2 特征选择模型及其优化算法

2.1 正则互表示无监督特征选择模型

通过将X={f1，f2，…，fn}中的每一个特征进行重构，可得如下结果：

式中：Wo为权重矩阵，上标o是指权重矩阵W的对角线元素都为0，这是因为特征不参与自身的线性近似表示，所以权重系数为0；E为残差矩阵，表示原始数据X重构前后的残差。

从向量的角度分析，残差矩阵E由残差向量的有序集合{e1，e2，e3，…，en}组成，每个特征重构前后的残差使用度量。将残差度量标准由向量推广到矩阵时，可以使用度量原始数据X重构前后的残差大小。本文期望重构后的数据XWo能够很好地近似表示原始数据X，因此残差越小越好，对应的目标函数为：

目标函数式（3）的优化问题属于无偏估计回归问题，在无偏估计回归问题中，当数据矩阵X不是列满秩的，或者某些列之间线性相关性比较强时，得到的最优解将会不稳定。为了解决这个问题，在目标函数中加入一个正则项对权重矩阵的解空间进行约束，使计算出的最优解更稳定。基于上述分析，改进后的目标函数为：

本文把包含权重矩阵正则项的目标函数式（4）称为正则互表示（Regularized Mutual Representation，RMR）无监督特征选择模型。

2.2 分治-岭回归优化算法

针对提出的RMR 特征选择模型，为之设计一种高效的优化算法，该算法结合了分治算法［14］和岭回归［15］优化算法，本文称之为分治-岭回归优化算法。本节首先证明以下定理。

定理1给定如下两个优化问题的目标函数：

其中：fi是X的第i列；是Wo的第i列。则整体优化问题的最优解可通过计算所有岭回归子优化问题的最优解得到。

证明 将数据矩阵X按列数分解为特征的有序集合{f1，f2，…，fn}，将权重矩阵按列数分解为权重向量的有序集合{ω1，ω2，…，ωn}，则有：

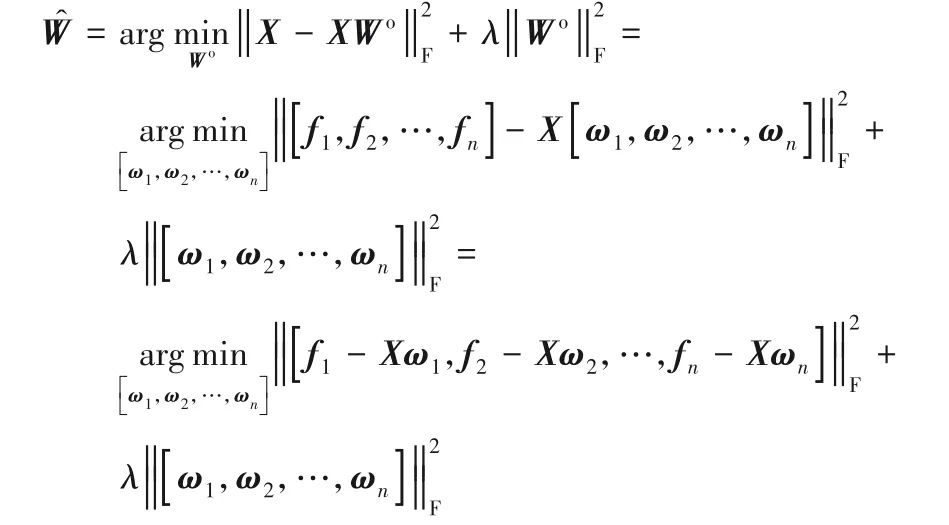
因为矩阵的Frobenius 范数的平方等于矩阵中所有列向量l2-范数平方的和，因此上式中可继续变形为：

至此可知，只要使得分解后的每个岭回归子优化问题都取得最优解，即可保证整体优化问题取得最优解。

定理1证毕

分治-岭回归优化算法首先利用分治算法的思想，将整体优化问题分解为若干个子优化问题；然后针对每个子优化问题利用岭回归优化算法计算最优解；最后将各个子优化问题的最优解进行整合，得到整体优化问题的最优解。

分治-岭回归优化算法的具体计算步骤如下。

首先，将RMR 模型的整体优化问题按照数据矩阵X的每个特征，分解为如下的n个岭回归子优化问题：

式中：i=1，2，…，n。第i个子优化问题的最优解用于重构特征fi，使得重构前后的误差最小的第i个元素为0，因为特征fi不参与自身的线性近似表示。

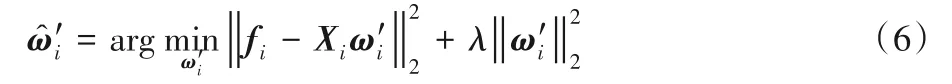
式（6）中的Xi是由X去掉特征fi得到，式（6）中的由式（5）中的ωi删除第i个元素得到。目标函数式（6）的优化问题是岭回归优化问题，该优化问题的损失函数以及推导过程如下：

由于岭回归优化问题的损失函数是一个光滑的凸函数，因此可以在导数为0 处求得损失函数的最优解，即能够使残差L(ei)最小的解析解。最优解的推导过程如下：

令L(ei)对求偏导，得：

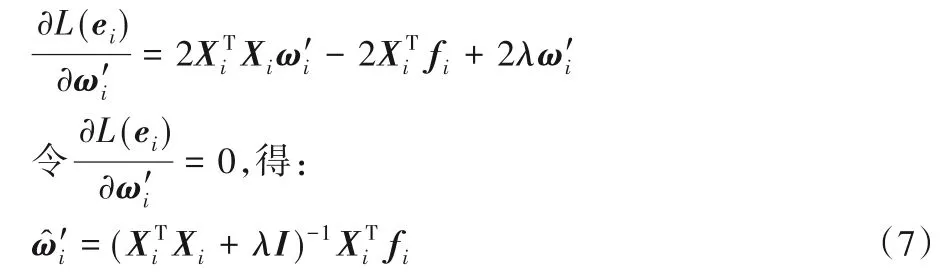
式中：I是单位矩阵；λ是正则项参数，且λ＞0。

总结上述分治-岭回归优化算法的具体计算步骤，得到RMR特征选择方法的计算框架1。

输入 数据集X，正则项参数λ，特征选择数量k；

输出 特征子集S。

3 实验验证与结果分析

3.1 实验数据集

实验中使用的数据集来源于UCI 标准数据集，共5 个数据集，关于这些数据集的详细描述信息请参考表1。

表1 实验数据集Tab.1 Experimental Datasets

表1中的Iris20 数据集为合成数据集，它是由UCI 标准数据集Iris 扩展而成，前4 列是Iris 数据集初始数据，后16 列数据是由前4 列进行随机线性组合得到，线性组合系数和为1，并在后16列数据中加入高斯白噪声。

3.2 评价指标

3.2.1 聚类准确率

使用K-Means 算法［16］对数据进行聚类，并计算数据样本聚类之后的准确率，聚类准确率（ACCuracy of clustering，ACC）的值越大说明聚类结果越好。ACC计算公式如下：

式中：m是样本个数；li是第i个样本的实际标签；map(ri)是第i个样本的聚簇标签，该函数使用Kuhn-Munkres 算法计算样本的聚簇标签；函数f(a，b)用于判断标签a和标签b的值是否相等，若相等则函数值为1，不相等则函数值为0。

3.2.2 归一化互信息

归一化互信息（Normalized Mutual Information，NMI）是评价聚类结果好坏的常用指标之一，用于度量聚簇标签向量与实际标签向量的一致程度，NMI 值越大说明聚类结果越好。NMI计算公式如下：

式中：p是聚簇标签向量；q是实际标签向量；I(p，q)是向量p与q之间的互信息；H(p)和H(q)分别是p和q的信息熵。

3.2.3 冗余率

冗余率（Redundancy rate，Rr）用于度量数据的特征之间是否具有较强的相关性，相关性越强说明数据冗余程度越高，因此冗余率越小越好。Rr计算公式如下：

式中：S是特征子集；n是特征子集的特征数量；βi，j是特征fi和特征fj的皮尔逊相关系数。

3.3 实验设置

为了验证所提出的RMR 无监督特征选择方法的有效性和高效性，实验中使用另外四种无监督特征选择方法用于对比，对比方法分别为经典的Laplacian 特征选择方法［17］、使用了谱分析技术的非负判别特征选择（Nonnegative Discriminative Feature Selection，NDFS）方法［18］、引入了正则约束的RSR 方法和自表示特征选择（Self-Representation Feature Selection，SR_FS）方法［19］。

每种特征选择方法从每个数据集中选出9 个不同维数的特征子集，选出特征数量依次是特征总数量的1/10，2/10，…，9/10，然后取这9 个不同维数的特征子集的聚类准确率平均值、归一化互信息平均值以及冗余率平均值，作为评价该特征选择方法效果优劣的三项指标。对于目标函数中有正则项的特征选择方法，将正则项参数的值域设置为｛0.01，0.1，1，10，100｝，对每个正则项参数均进行实验并选取最佳结果。

另外，针对聚类准确率这一评价指标，由于K-Means 聚类算法得出的聚类准确率会受初始质心选取的影响，为减少随机误差的影响，提升结果准确度，对每个特征子集进行100 次聚类，然后取100 次聚类准确率的平均值作为该特征子集的聚类准确率。

3.4 结果分析

首先，将本文提出的RMR 方法应用在Iris20 合成数据集上，因为Iris20 数据集的后16 列数据是由前4 列数据组合得到，且加入了一定的噪声，因此后16 列数据是应当剔除的冗余特征，而前4 列数据为特征选择方法应当识别出的重要特征。

图1 是RMR 方法计算出的Iris20 特征权重直方图，横轴代表Iris20 数据集的20 个特征，纵轴代表计算出的各个特征的权重。权重越大，特征越重要，越具有代表性。从图1 可以直观地看出，前4个特征的权重明显大于后16个特征的权重，这说明RMR 方法可以有效地识别出数据集中具有代表性的特征。从表2 的实验结果数据可以得知，RMR 特征选择方法与其他四种特征选择方法相比，其在5 个标准数据集上选出的特征子集的平均聚类准确率最大，说明RMR 方法对聚类准确率的提升能力更强。从表3 的实验结果数据可以看出，RMR 方法选出的特征子集的归一化互信息NMI 值最大，说明RMR 方法选出的特征子集的聚类效果更好。无论是聚类准确率还是归一化互信息，都是度量聚类结果好坏的常用指标，值越大越好。因此从表2 和表3 可以得出相同的结论，使用RMR 方法对原始数据集进行特征选择，可以选出数据中的具有代表性的特征，有效地改善数据在聚类时的表现，并且同其他四种对比方法相比效果更好。

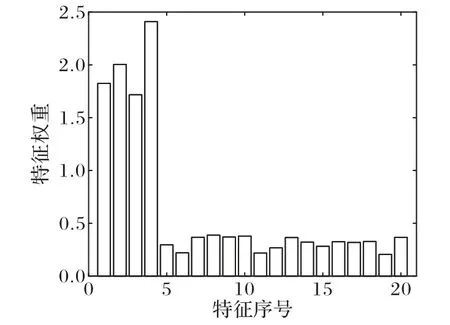
图1 Iris20特征权重直方图Fig.1 Histogram of feature weights of Iris20

表2 聚类准确率对比 单位：%Tab.2 Comparison of clustering accuracy unit：%

表3 归一化互信息对比 单位：%Tab.3 Comparison of normalized mutual information unit：%

从表4中的实验结果可知，RMR 方法与另外四种特征选择方法相比，其所选出的特征子集的冗余率最低，说明RMR方法从原始数据中选出的特征相关性较弱，数据冗余程度更低。

表4 冗余率对比 单位：%Tab.4 Comparison of redundancy rate unit：%

RMR 方法选出的特征子集之所以具有较好的聚类表现和较低的冗余程度，是因为RMR 模型是基于正则互表示性质，利用了特征间的相关性，同时克服了特征权重容易向自身倾斜的缺点。RSR方法和SR_FS方法虽然利用了特征间的相关性，但是忽视了特征权重容易向自身倾斜的问题。NDFS方法结合谱聚类技术进行特征选择，该方法的效果依赖于样本相似性矩阵，容易受其影响。Laplacian 方法没有考虑特征间的相关性，因此无法有效识别冗余特征。

在计算复杂度方面，RMR 数学模型中的误差项和正则项都是使用矩阵Frobenius 范数进行约束，使用分治算法将矩阵优化问题转换为若干个向量优化问题，如式（5）所示。此时的向量优化问题是岭回归优化问题，目标函数中的误差项和正则项均由向量l2-范数约束，l2-正则是凸形正则，可以在导数为0处直接取得使残差最小的解析解，如式（7）所示，式中：的计算复杂度是O(mn2)；求逆运算的复杂度是O(n3)；的复杂度是O(mn)；矩 阵与向量相乘的复杂度是O(n2)。考虑到样本数量大于特征数量（即m＞n），所以单个岭回归优化的总体渐进复杂度为O(mn2)。因为整体优化问题被分解为n个岭回归子优化问题，所以RMR 方法的整体优化问题的渐进计算复杂度为O(mn3)。RMR 方法计算特征选择模型最优解的过程仅相当于一次矩阵迭代运算，而非多次迭代，而NDFS 方法、RSR 方法以及SR_FS 方法都是采用矩阵多次迭代的方式逼近最优解，每一次迭代都会涉及大量的矩阵运算，计算复杂度与迭代次数成正比。因此，RMR 方法具有更低的计算复杂度，在计算性能上更具优势。

4 结语

本文研究利用高维无标签数据特征之间的相关性进行特征选择，通过在特征选择时对特征权重施加正则约束，提升了特征选择结果的鲁棒性，解决了特征权重分配不合理导致无法有效识别冗余特征的问题。实验结果表明，RMR 方法能够选出重要特征，减少数据冗余，提升聚类精度。算法理论复杂度分析表明，所提方法因使用分治-岭回归优化而具有较低的计算复杂度。RMR 方法也存在不足之处，其未考虑数据集的样本数量少于特征数量的情况，未来研究可考虑高维小样本数据情况下如何改进。