融合主题信息和卷积神经网络的混合推荐算法

田保军，刘 爽，房建东

（1.内蒙古工业大学信息工程学院，呼和浩特 010080；2.内蒙古工业大学数据科学与应用学院，呼和浩特 010080）

（*通信作者电子邮箱ngdtbj@126.com）

0 引言

随着互联网信息的指数型增长，用户的选择更加多样化，这样虽能更好地满足用户需求，但是快速查询所需要的信息变得越来越困难。为了帮助用户摆脱困境，推荐系统［1］应运而生，其中协同过滤推荐［2］和基于内容的推荐［3］是当前推荐系统的两种主流技术，但这两种方法都存在着诸多缺点。其中，数据稀疏性是传统的协同过滤模型存在的主要问题［4］，而基于内容的推荐获取的又是浅层特征，不能很好地描述用户与项目的行为［5］，导致推荐精度不高。深度学习模型恰好能够提取到深层次的特征，将深度学习能够学习到的稠密、连续、多层次的用户和项目的特征，例如：近邻关系、主题关系以及用户的评论和标签信息等［6-9］，与协同过滤推荐融合，使得混合推荐系统不仅具有传统推荐方法的简单、可解释性强等优点，而且使得推荐精度更高。目前，传统的推荐算法与深度学习算法进行结合已经成为越来越多的研究者关注的研究热点［10］。

Kim 等［11］提出了基于卷积矩阵因子分解（Convolutional Matrix Factorization，ConvMF）模型，利用卷积神经网络（Convolutional Neural Network，CNN）处理项目的文本信息，学习到项目的隐特征，融入到通过PMF 模型分解的评分矩阵中，提高了评分预测的准确性。但是该方法仅仅根据评论的原始文字来提取项目的连续全局特征，忽略了文档中显著的主题特征信息。Liu 等［12］提出了一种改进的基于主题模型隐狄利克雷分布（Latent Dirichlet Allocation，LDA）的协同过滤算法。该算法根据用户项目评分矩阵建立LDA 模型，获取用户多个显著特征单独表示信息，得到用户项目选择概率矩阵，然后按照项目属性对项目集进行聚类，根据聚类结果对矩阵进行裁剪。实验结果表明，主题模型可以有效地提高推荐的精度。张敏等［13］将评论信息引入推荐系统中，提出栈式降噪自编码器（Stacked Denoising AutoEndoder，SDAE）与隐含因子模型（Latent Factor Model，LFM）相结合的混合推荐方法，进一步地提升了推荐模型对潜在评分预测的准确性。Hyun等［14］提出了一个可扩展评论感知的推荐方法SentiRec（Sentic Reccommendation），它在建模用户和项目时被引导结合评论的情感。该方法分两步：第一步将每篇评论编码成一个固定大小的评论向量，这个向量经过训练以体现评论的观点；第二步根据向量编码的评论生成推荐。实验结果表明，该方法不仅优于现有的神经网络推荐方法，而且推荐效果优于仅仅考虑评论上下文连续特征的方法。Chen 等［15］提出了一种联合神经协同过滤推荐系统的方法，它是一种将深度特征学习和深度交互建模与关联矩阵相结合的联合神经网络。深度特征学习基于用户-项目评分矩阵，通过深度学习架构提取用户和项目的特征表示，联合训练使深度特征学习和深度交互建模过程相互优化，从而提高推荐性能。

综上所述，利用深度学习技术、融合多源异构数据成为提高推荐系统准确性的一种重要方法，但是已有相关研究还存在很多问题。其中，从项目评论信息提取的项目特征面临着艰巨的问题就是辅助数据的表示，辅助数据表示还存在着单一性和准确性不高问题。

针对以上问题，本文提出了一种基于隐狄利克雷分布（LDA）与CNN 的概率矩阵分解推荐模型（Probability Matrix Factorization recommendation model based on LDA and CNN，LCPMF）。该模型综合考虑项目评论文档的主题信息与深层语义信息，分别使用LDA 主题模型和文本卷积神经网络对项目评论文档建模，获取项目评论文档的显著潜在低维主题信息及全局深层语义信息，接着通过线性加权组合得到项目隐因子矩阵，最后融合到PMF 概率矩阵分解PMF 模型中，产生预测评分进行推荐。通过实验将本文提出的新推荐模型LCPMF 与经典的PMF、协同深度学习（Collaborative Deep Learning，CDL）与ConvMF 等模型进行实验结果对比，验证了本文提出模型的可行性和有效性。

1 相关理论

1.1 基本概率矩阵分解

基于矩阵分解的推荐模型是隐含语义模型的一种方法，属于基于模型的协同过滤算法［16］，概率矩阵分解模型是协同过滤的算法中最具代表性且广泛使用的，它的基本思想是通过分解评分矩阵再重构的方式补全评分矩阵中的不可观测值，具体来说，首先构建“用户-项目”矩阵R并将其分解为两个低维的矩阵U、矩阵V的乘积方式，然后通过U和V的内积来重构新的评分矩阵，这样原始的评分矩阵R中没有评分的项目也有了相应的评分，将用户已经评分的项目剔除掉，根据“重构”出的分值对剩余项目的评分进行排序即可得到最终的项目推荐列表，其目标函数为：

其中：Rij为真实评分；UTi Vj为预测评分；λU与λV为正则化参数，用来防止过拟合；n与m分别代表n个用户与m个项目；Iij为指示函数，有评分时为1，没有评分时为0。

在推荐系统中，真实的用户对项目的评分矩阵通常是非常稀疏的，例如Amazon 数据集的稀疏度为0.03%，这导致推荐的预测评分准确率较差。针对概率矩阵分解模型中数据稀疏和准确性问题，引入了辅助信息——项目评论文档，优化概率矩阵分解模型，从而缓解用户评分的稀疏性。

1.2 主题模型

LDA 是一种文档主题生成模型，也称为一个三层贝叶斯概率模型，包含词、主题和文档三层结构。所谓生成模型，就是说，认为一篇文章的每个词都是通过“以一定概率选择了某个主题，并从这个主题中以一定概率选择某个词语”这样一个过程得到。文档到主题服从多项式分布，主题到词服从多项式分布［17］。因此，由同一主题下某个词出现的概率，以及同一文档下某个主题出现的概率，两个概率的乘积，可以得到某篇文档出现某个词的概率，如图1所示。

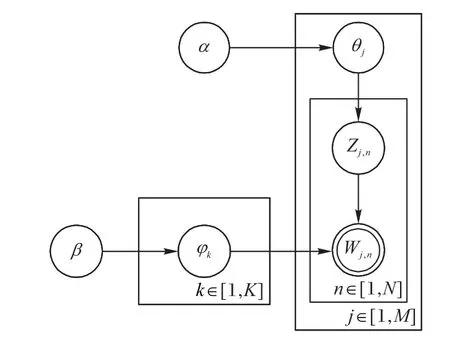
图1 LDA主题模型结构Fig.1 LDA topic model structure

因此在LDA模型中，一篇文档生成的方式如下：

1）从狄利克雷分布α中取样生成文档j的主题分布θj；

2）从主题的多项式分布θj中取样生成文档j第n个词的主题Zj，n；

3）从狄利克雷分布β中取样生成主题Zj，n对应的词语分布φk；

4）从词语的多项式分布φk中采样最终生成词语Wj，n。

在推荐系统的研究中，有学者将主题模型用于基于隐因子模型的推荐算法中，但是当辅助信息稀疏时，它不能够获取有效以及充分的辅助数据表示，提升的效果有限。

1.3 卷积神经网络

卷积神经网络（CNN）通常应用于计算机视觉领域做图像分类、检测，以及自然语言处理等任务［18-19］。近年来，卷积又被引入推荐系统，并取得了很好的效果。网络结构由嵌入层、卷积层、池化层和输出层这四个部分构成，可以隐式地从训练数据中进行学习特征，如图2所示。

图2 卷积神经网络结构Fig.2 Convolutional neural network structure

在之前的推荐系统研究中，也有学者将卷积神经网络用于基于隐因子模型的推荐算法中，它可以学习用户或者项目的隐藏特征，如Kim 等［11］使用卷积神经网络学习项目评论文档中的隐特征，然后使用学习到的特征与PMF 结合用于推荐，虽然神经网络学习到了项目文档的深层语义信息，但它同样忽略了项目文档的显著主题特征表示，不能获取项目文档的多层描述，导致了项目评论文档特征表示提取的不全面。

2 LCPMF算法描述

本章主要从以下三个方面介绍基于LDA 与CNN 的概率矩阵分解推荐算法（LCPMF）。

1）介绍融合CNN 与LDA 的具体思想过程（LDA and CNN，LC）模型，并通过分析项目评论文档生成项目文档的潜在特征表示；

2）介绍融合LDA与CNN的概率图模型，描述PMF模型和融合模型LC结合的主要思想，建立被优化之后的项目特征条件概率。

3）给出模型优化之后的目标函数以及求解过程。

2.1 融合主题和卷积神经网络的评论文本建模

已有的相关性研究中从项目评论文档提取的项目特征表示还存在着单一性和准确性不高问题。综合考虑评论主题特征与深层语义信息，本文首先使用word2vec与Glove构建词向量模型，它可以快速地构建单词的词向量模型［20］，把原先的词嵌入到一个新的空间，能有效地表征词的语义信息。建立词向量模型之后，分别使用LDA 主题模型和文本卷积神经网络对项目评论文档建模。

2.1.1 评论文档LDA建模

LDA 是一种基于概率模型的主题模型算法，用来识别文档中隐含的主题信息。LDA主题模型虽然忽略了特征之间的联系，但是可以获取项目评论文档的多个显著特征单独表示。使用LDA 构建项目评论文档潜在主题表示，在项目评论文档数据集中，每一行为一个项目的所有评论，每一个项目的评论代表了一些主题所构成的一个概率分布，而每一个主题又代表了很多单词所构成的一个概率分布，从而将文本信息转化为了易于建模的向量信息。针对于每个项目的评论文档，从项目评论的全部主题分布中提取其中一个项目评论主题分布，从被抽到的项目主题下的单词分布中提取一个单词，直至遍历整个评论文档中的每个单词，LDA 认为每篇文档是多个主题混合而成，而每个主题可以由多个词的概率表征，主题模型LDA的核心公式为：

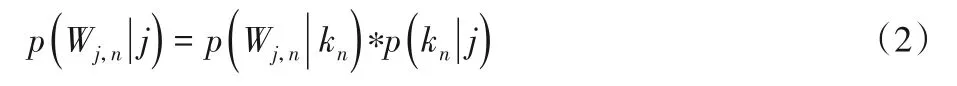
其中：Wj，n表示项目评论j中的第n单词；kn表示单词对应的主题。本文生成项目评论文档-主题向量过程如下：

步骤1 输入为项目评论文档Yj，对每一篇项目评论文档，Yj从项目主题分布中抽取一个主题。

步骤2 从已经被抽到的项目主题所对应的单词分布中抽取一个单词。

步骤3 重复步骤1～2直至遍历文档中的每一个单词；最后输出主题模型、主题词文档、词概率文档、文档主题文档、主题概率文档。

步骤4 先对每个主题下对应的单词分别进行词向量表示，并与对应的概率进行相乘；然后进行加权得到主题词向量表示。

步骤5 对每个文档下的主题概率与主题词向量进行乘积表示，加权得到文档主题向量表示。

步骤6 输出项目评论文档潜在主题表示向量。

2.1.2 评论文档CNN建模

卷积神经网络CNN 模型虽然不能挖掘项目评论文档中关键性和代表性信息，但是它可以获取全局信息以及上下文的之间的联系。CNN模型中的多层卷积可以获取项目评论文档中词语之间的相互关联，并学习到项目的全局信息以及上下文的之间的联系，继而得到项目的隐表示，具体过程如下所示：

1）嵌入层。

本文实验的项目评论文档的最大长度max-length设置为300，每个单词的词向量维度为200 维，组成词向量矩阵如式（3）所示。

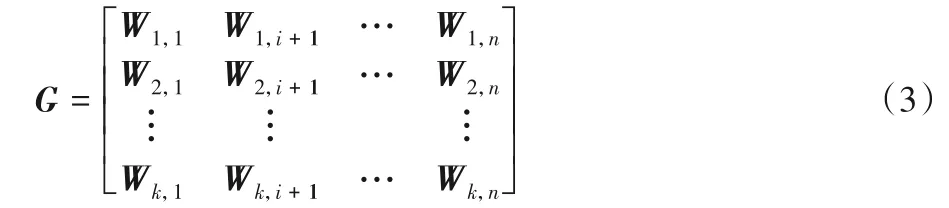
其中：W1，i为词向量；G表示由词向量组成的矩阵。

2）卷积层。

在卷积层中，对词向量矩阵G提取特征，卷积中使用的滑动窗口大小分别为3、4、5，得到不同文本卷积神经网络的卷积操作可以用式（4）表示：

其中：A表示某个卷积核上的激活值；wi，j是权重；relu为本文采用的激活函数；G表示卷积层的输入词向量矩阵。

经过以上的卷积操作，卷积层的输出公式如下：

其中，A为经过不同卷积核形成的项目评论文档新特征，作为卷积池化层的输入。

3）池化层。

池化层采用最大池化，池化的大小为(300-滑动窗口+1) ×1，每一个卷积核对应一个值，把这些值拼接起来，就得到一个表征该句子的新特征量。

4）输出层。

在输出层中，将新特征量映射成最后的项目隐特征表示。利用卷积神经网络将原始的项目评论文档转换成项目特征向量，输出项目评论文档的深层语义表示矩阵，用式（6）向L维空间进行映射：

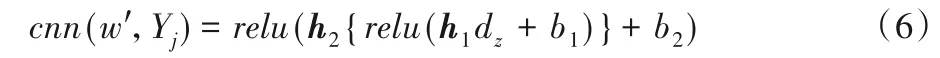
其中：h1、h2为映射矩阵；b1、b2为偏置；dz为池化层的输出；Yj为卷积神经网络的输入；w'为卷积神经网络的参数，最后卷积神经网络的输出维度要与概率矩阵分解PMF 模型中的隐特征向量维度相等。

2.1.3 融合LDA和CNN获取项目的多层次表示

使用LDA 模型和CNN 模型获取相同维度的项目潜在低维主题信息及深层语义信息之后，考虑了项目评论文档局部的潜在的主题特征，同时也注意到推荐也会受到项目评论的全局的深层语义影响。为了同时综合考虑两者的关系，使用线性函数将两者关联起来，加权整合主题信息及语义信息得到新的项目评论文档特征，如式（7）所示：

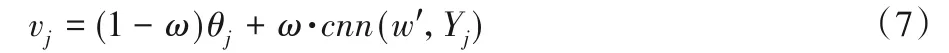
其中：cnn(w'，Yj)为经过卷积神经网络CNN 处理得到的文档的特征；θj为通过主题模型LDA 提取的文档的主题特征；ω为权重。LDA主题模型可以获取项目评论文档多个显著特征单独表示，忽略了特征之间的联系，而CNN中不能挖掘文档中关键性和代表性信息，但是可以获取全局信息以及上下文的之间的联系。通过线性函数将两者结合起来，得到新的项目评论文档向量，对于项目评论文档，既考虑了项目评论文档的局部信息，又考虑了项目评论文档的全局信息，得到项目评论文档的多层次表示，解决项目评论文档特征提取不全面问题。接下来，将两个模型融入概率图模型PMF中。

2.2 融合主题和卷积神经网络的概率图模型

针对传统的协同过滤算法中数据稀疏性和推荐结果不准确性问题，提出了基于LDA 与CNN 的概率矩阵分解推荐模型（LCPMF）。

2.2.1 构建模型LCPMF

算法首先使用基于线性关系的LDA 主题模型与CNN（LC模型）提取项目评论文档多层次特征表示Yj；然后将多层次特征应用于项目的隐因子V中，其中LDA 主题模型输出与CNN输出都与PMF的隐因子个数相同；最后，使用用户的隐因子U和物品的隐因子V重构评分矩阵R，如图3所示。

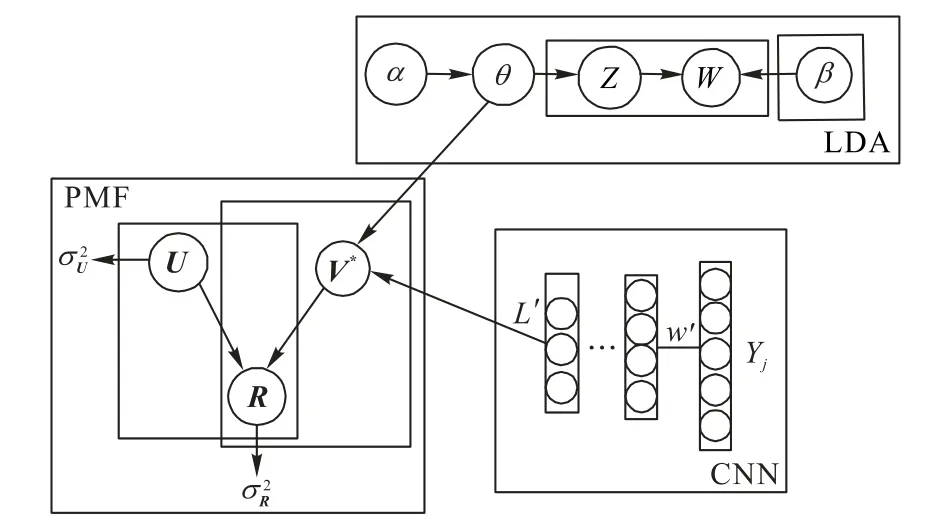
图3 LCPMF概率图Fig.3 Probability diagram of LCPMF

图3中，R为评分，U、V分别为用户与项目特征，θj为主题分布，Yj为卷积神经网络的输入，w'为权重，L'为卷积神经网络的输出。

对于传统的概率矩阵分解模型PMF，用户对项目的评分Rij的条件概率分布为：

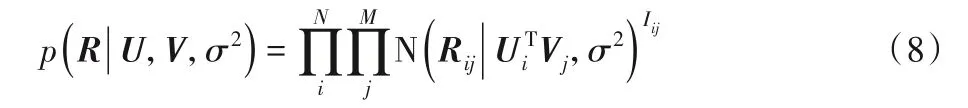
其中：Rij服从均值为μ、方差为σ2的高斯正态分布的概率密度函数；Iij是指示函数，如果有评分为1，否则为0。

同时假设用户隐特征均服从μ=0、σ2=σ2U的高斯先验。

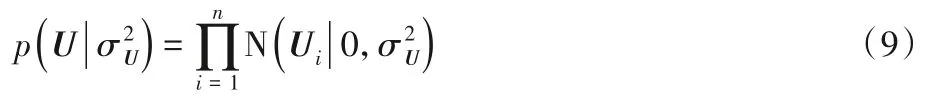
和传统PMF 算法中不同的是：项目的隐特征向量不再由高斯分布生成，而是由四个变量构成，分别是：项目评论文档Yj，卷积神经网络权重w'，主题分布θj，高斯噪声ρj。因此，被优化之后的项目隐特征的条件概率表达式为：

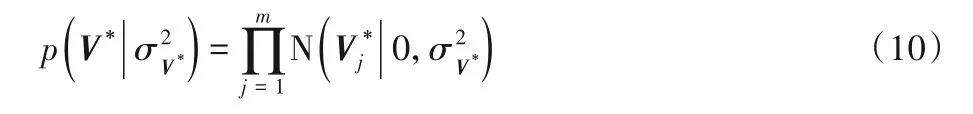
其中V*的构成如下所示：

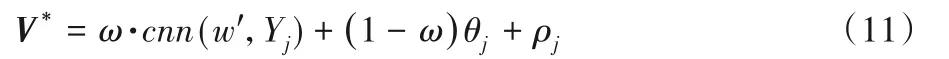
V*表示融合LDA与CNN的项目特征向量，对于所有项目评论文档运用LDA生成的主题分布服从θj～Dirichlet(α)。

令卷积神经网络w'与高斯噪声ρj也服从高斯分布：

从LC 模型提取的项目评论文档的多层次表示特征向量作为项目的隐因子，其中项目的隐因子满足均值为ω·cnn(w'，Yj)+(1-ω)θj，方差为ρj的高斯分布。

2.2.2 模型优化

为了优化用户隐因子的提取、项目偏差变量和LC的隐向量，使用最大后验估计，根据贝叶斯公式可得：

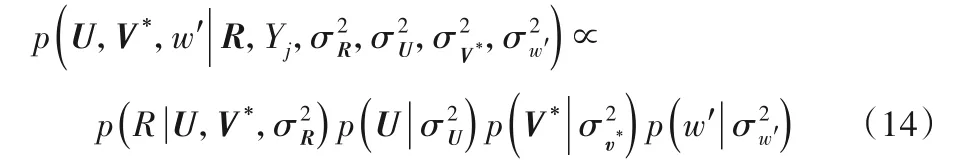
其中：U、V*分别代表用户和优化之后的项目；R代表评分矩阵；Yj为卷积神经网络与主题模型的输入，ω代表衡量卷积神经网络与主题模型的权重系数。

对式（14）取对数，可得最终的目标函数如下所示：

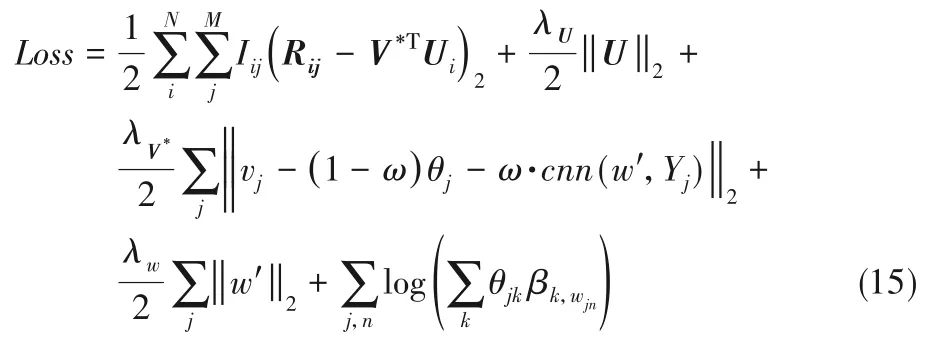
其中：Rij为处理之后的原始矩阵；(ω·cnn(w'，Yj)+(1-ω)θj)TU为预测评分；U、V*各代表用户与项目的特征；w'为卷积神经网络的权重；Yj为卷积神经网络的输入；wkn代表单词；K为主题；θjk为第j个项目的主题分布，且，。

根据Loss 损失函数进行求解时，采用梯度下降法对用户隐向量和项目隐向量进行更新。更新表达式如下：

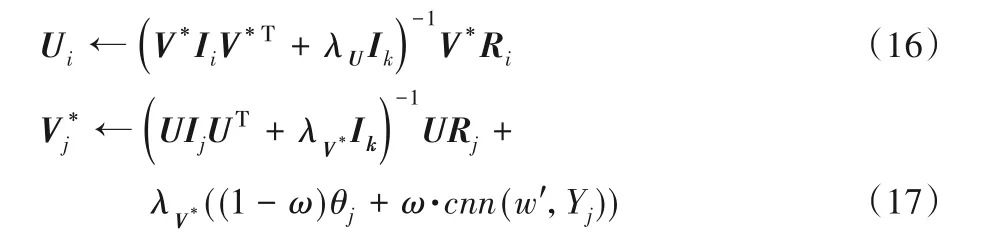
其中：Ik为对角矩阵；λU与λV*为正则化参数。式（17）中影响项目的潜在向量为CNN 模型与LDA 模型融合之后的项目评论文档特征。在给定U和V*之后，根据优化之后的项目隐特征向量与输入时的项目特征隐向量的误差，采用误差反向传播算法更新卷积神经网络的参数。

2.2.3 算法总体流程

基于LCPMF的推荐算法流程如下所示。

3 实验与结果分析

3.1 实验环境

采用 GPU Tesla P100-PCIE-12GB；操作系统为Ubuntukylin-16.04-desktop-amd64；编程环境使用Pycharm 2018.3.1 x64；开发语言为Python 2.7；深度学习框架为Keras 2.2.4；后端使用TensorFlow 1.8.0。

3.2 实验评价标准

为了评估模型的总体性能，采用均方根误差（Root Mean Square Error，RMSE）、平均绝对偏差（Mean Absolute Error，MAE）作为评价标准。通过预测值和真实值之间的差距来反映推荐模型的好坏，MAE与RMSE值越小，代表着推荐结果的精度就越高。本文采用上述两种方式进行，具体计算式如下：

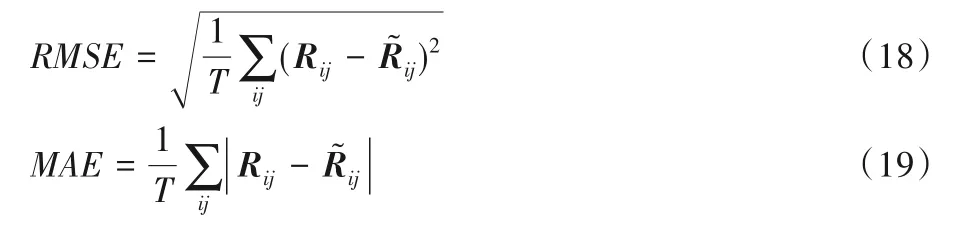
其中：T表示测试集评分记录数；Rij表示用户i对项目j的真实评分；表示用户i对项目j的预测评分值。

3.3 实验结果分析

本文中采用的数据集为Movielens 1M、Movielens 10M 和Amazon 真实数据集。数据集中包括用户项目的打分。Amazon 数据集包含评论文档。Movielens 数据集中的评论文档从IMDB数据集中获取，数据集详细描述如表1所示。

将实验数据集按照8∶1∶1 的比例分为训练集、验证集与测试集，分别计算MAE的值和RMSE的值。

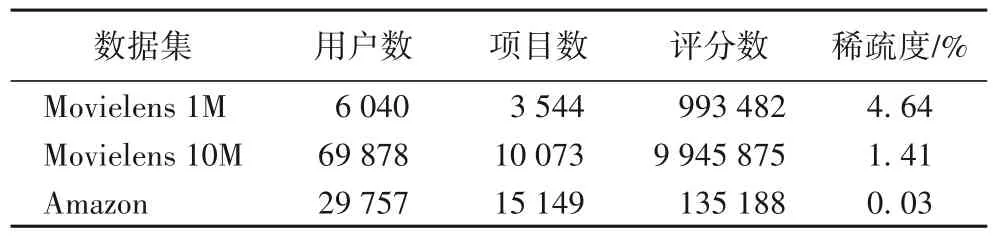
表1 实验数据集详细描述Tab.1 Detailed description of experimental datasets

本文主要考虑以下几个主要参数对算法的影响：

1）卷积与主题模型的权重ω对模型的影响。

首先，评测卷积与主题模型的权重ω对模型的影响，参考ConvMF 和深度学习在自然语言处理中的研究，假定K=5，α=0.5，β=0.01，L=50，λU=90，λV*=10。

分析参数ω对实验评价标准RMSE 值的影响，实验结果如图4 所示。从图4中可以得出：在确定主题LDA 模型参数K=5，α=0.5，β=0.01，隐特征向量维度L=50，正则化参数λU=90，λV*=10的情况下，RMSE的值将随着ω的值先下降再升高，当ω=0.5时达到最小，之后再增加。

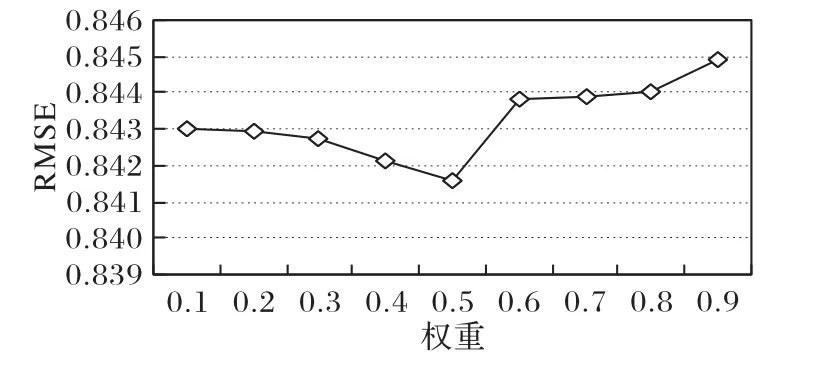
图4 参数ω对RMSE的影响Fig.4 Influence of parameter ω on RMSE

分析参数ω对实验评价标准MAE 值的影响，实验结果如图5所示。从图5中可以得出：MAE的值随着权重参数ω的增加是先下降，之后一直升高，在项目隐向量特征中，LDA 主题特征占据较小的权重相较CNN 语义特征占据较小的权重时，前者推荐精度较好，但是当ω=0.5时，RMSE 与MAE 取最小值。

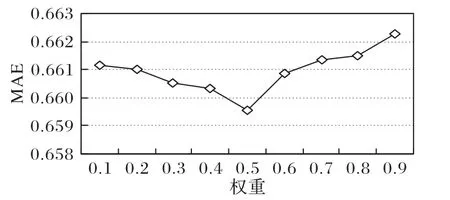
图5 参数ω对MAE的影响Fig.5 Influence of parameter ω on MAE

通过以上两组实验，可以看出CNN 与LDA 提取项目评论文档的特征表示具有差异性和互补性；而且，利用这一点将它们的特征表示融合之后，获取项目文档多层次的表示，提升了推荐系统的准确性，解决了项目评论文档特征提取不全面问题。

2）正则化参数λU与λV*对模型的影响。

通过上述实验，在ω=0.5的情况下，RMSE 与MAE 取得最小值。因此，在同样条件下，采用此参数调节正则化参数λU与λV*的实验。从表2中可以看出，当λV*=10时，随着λU的不断增大，RMSE 和MAE 在不断减小；当λU=90时，RMSE 与MAE 取得极小值。当λU=90时，λV*不断增大时，RMSE 和MAE 反而增高了，说明当λU=90，λV*=10时，RMSE 与MAE 达到最小值。

3）LDA主题个数K对模型的影响。

通过上述实验，在λU=90，λV*=10的情况下，RMSE与MAE取得最小值，因此，在相同条件下，采用此参数进行主题个数K的最优取值实验，K值采用0、5、10、15、20、25。

分析主题个数K对实验评价标准RMSE 值的影响，实验结果如图6 所示。从图6中可以看到，当K=0时，只利用CNN 提取了项目评论的全局的深层语义影响，也就是经典的ConvMF 模型，但此时的RMSE 达到最大值，效果最差。图中的折线呈现出先下降再上升的趋势，当主题个数K=5时，RMSE达到最小值。

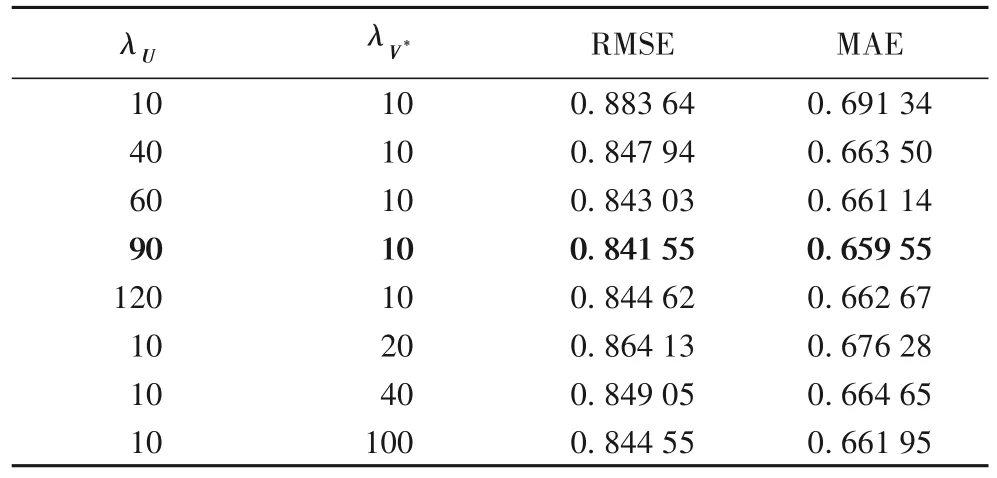
表2 参数λU与λV*对RMSE、MAE的影响Tab.2 Influence of parameter λU and λV*on RMSE and MAE

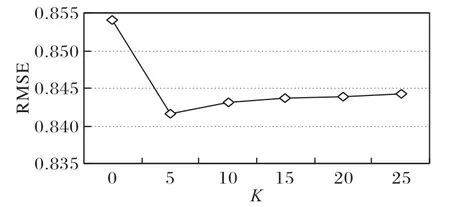
图6 参数K对RMSE的影响Fig.6 Influence of different parameter K on RMSE

分析主题K对实验评价标准MAE 值的影响，实验结果如图7所示。从图7中可以得出：MAE的值随着主题个数K的先下降再升高，同时在K=5时，MAE取最小值。

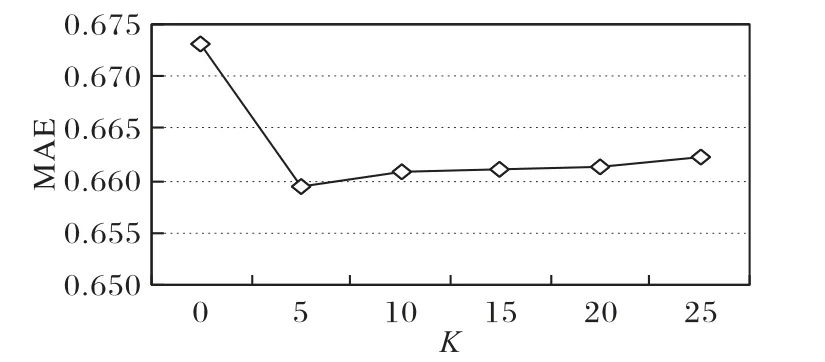
图7 参数K对MAE 的影响Fig.7 Influence of different parameter K on MAE

通过以上两组实验，使用线性函数加权整合主题信息及语义信息得到新的项目评论文档特征，可以明显地提高推荐的准确性，证明了综合考虑LDA 提取的评论文档的主题特征和CNN提取的评论文档全局特征两者的关系是可行的。

4）隐特征维度L对模型的影响。

通过上述实验，在主题个数K=5 的情况下，RMSE 与MAE取得最小值，因此，在相同条件下，采用此参数进行对隐特征维度L值的实验，隐特征维度L分别采用25、50、75、100。

分析隐特征维度L对实验评价标准RMSE 值与MAE 值的影响，实验结果如表3 所示。从表3中可以看到：当隐特征维度L为25时，虽然花费时间较短，但是RMSE 与MAE 的值较高，准确度较低；当隐特征维度L为75和100时，虽然RMSE和MAE的值与50维度时相差不大，但是训练时间效率上远超过50 维。最后，综合考虑时间效率和准确度的因素，将隐特征维度L=50时作为维度选择的最优值。

5）项目文档最大长度max-length对模型的影响。

通过上述实验，在隐特征向量维度L=50 的情况下，RMSE 与MAE 取得最小值，因此，在相同条件下，采用此参数进行对项目文档最大长度max-length的实验，项目文档最大长度max-length分别采用50、100、200、300、350。

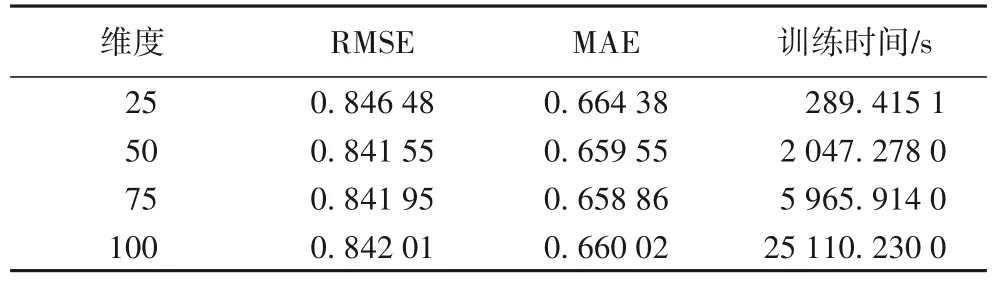
表3 参数L对模型性能的影响Tab.3 Influence of parameter L on model performance

分析项目文档最大长度max-length对实验评价标准RMSE值与MAE值的影响，实验结果如表4所示。从表4中可以看到：当项目文档最大长度max-length较小时，RMSE 与MAE 的值较高，准确度较低；当项目文档最大长度max-length逐渐增大时，RMSE与MAE的值也逐渐降低，当项目文档最大长度max-length达到350时，RMSE 与MAE 的值反而又开始增大了。所以，当项目文档长度max-length=300时，RMSE 与MAE达到最优。

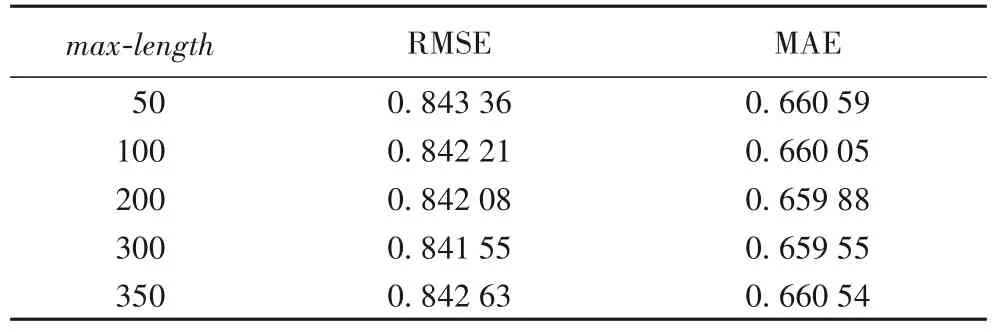
表4 参数max-length对RMSE和MAE的影响Tab.4 Influence of parameter max-length on RMSE and MAE

6）LCPMF与其他不同模型在不同算法的对比。

将本文所提出的LCPMF，与4 种经典模型：PMF 模型、使用深度学习SDAE 与PMF 结合的推荐模型（CDL）、使用CNN与PMF 结合的推荐模型（ConvMF），分别在Movielens 1M、Movielens 10M 和Amazon 三种数据集上，进行了实验评价标准RMSE值的比对，如表5所示。

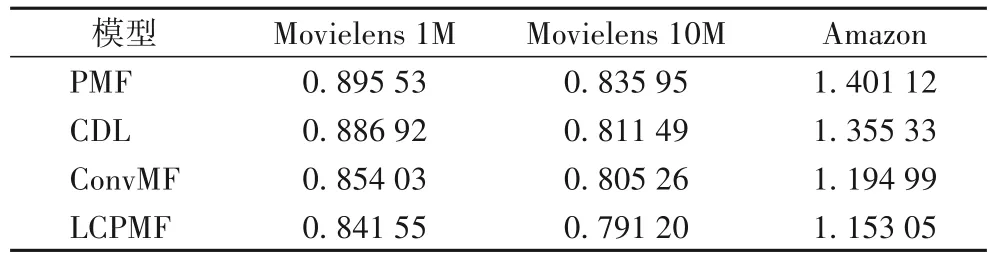
表5 不同算法在不同数据集下的RMSE对比Tab.5 RMSE comparison of different algorithms on different datasets

本文的模型LCPMF 在Movielens 1M、Movielens 10M 和Amazon 三种数据集与PMF、CDL、ConvMF 模型的实验评价标准MAE值比对，如表6所示。

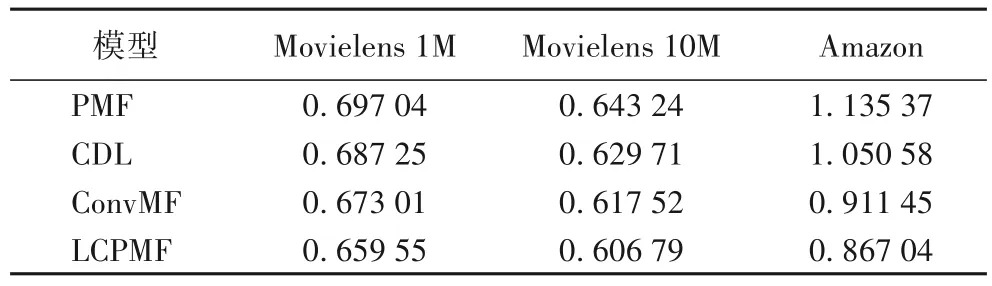
表6 不同算法在不同数据集下的MAE对比Tab.6 MAE comparison of different algorithms on different datasets

从表5 与表6中可以看出，与经典的PMF 模型、CDL 模型和ConvMF 模型相比，本文提出的算法在不同数据集中无论是RMSE 还是MAE 都有明显降低。相较PMF、CDL、ConvMF模型，所提推荐模型LCPMF 的均方根误差（RMSE）和平均绝对误差（MAE）在Movielens 1M 数据集上分别降低了6.03%和5.38%、5.12% 和4.03%、1.46% 和2.00%，在Movielens 10M 数据集上分别降低了5.35%和5.67%、2.50%和3.64%、1.75%和1.74%，在Amazon 数据集上分别降低17.71%和23.63%、14.92%和17.47%、3.51%和4.87%。这表明本文提出的基于LDA 与CNN 的概率矩阵分解推荐模型（LCPMF）是有效的，融合LDA 和CNN 的方法可以更准确地获得用户评论的特征表示，进一步提高推荐算法的准确性。

4 结语

本文提出了一种基于LDA 与CNN 的概率矩阵分解推荐模型（LCPMF）。该模型综合考虑评论主题与上下文信息，通过结合卷积输出的上下文特征和主题模型LDA 提取的主题特征，并使用权重系数决定两个特征定义新文档的影响程度，在一定程度上解决了数据稀疏和项目文本隐特征向量提取特征欠缺的问题，突出了用户对项目的偏爱程度，提高了推荐的准确性。在三种公开真实的数据集Movlens 1M、Movlens 10M和Amazon 上进行实验，使用MAE 和RMSE 指标作为评价标准，将本文模型与经典的模型PMF、CDL、ConvMF 进行对比，实验结果表明本文提出的模型在推荐质量上都有明显的提高，验证了该模型在推荐系统中的可行性与有效性。由于本文仅仅优化了项目隐特征向量的表示性问题，并没有对用户的隐特征向量进行优化，下一步可针对该问题进行研究。