基于区块链的安全电子选举方案

吴芷菡，崔 喆*，刘 霆，蒲泓全

（1.中国科学院成都计算机应用研究所，成都 610041；2.中国科学院大学，北京 100049）

（*通信作者电子邮箱cuizhe@casit.com.cn）

0 引言

随着现代信息技术的发展，社会对电子选举技术以及社会民主进步的关注日益增加。近年来，电子选举已经成为国际信息技术界一个特殊重要的领域。如今国际电子选举系统研究主要分为两个方向：一是基于远程网络通信的电子选举（Remote e-Voting），主要是基于数论的密码学工具和应用技巧，主要有基于同态加密的电子选举方案、基于秘密共享的电子选举方案、基于盲签名的电子选举方案和基于混合网络的电子选举方案；二是基于抵近物理站站点投票的电子选举（Site-Polling e-Voting），主要凭借物理设备和先进的信息技术手段实现高可信、高可靠的选举系统，例如应用于我国人民代表大会的选举系统。本文的研究方向是基于远程网络通信的电子选举。

基于同态加密的方案通过同态加密算法：ElGamal密码体制［1］、LWE（Learning With Errors）密码体制［2］和Paillier［3］密码体制对选票进行加密，然后由可信第三方计票机构接收和计算加密选票，文献［1-2］采用乘法同态、全同态运算，计算效率低，复杂度高，实用性较低。基于秘密共享［4-5］的方案通过将拆分后的选票发送至多个机构存储，由部分或全部机构恢复选票并统计结果，虽然多个可信任计票机构中心降低了单一权威计票机构内部欺诈的风险，但超过一定门限数量的机构串通仍可进行共谋攻击，控制选举。基于盲签名的方案有FOO（FUJIOKA-OKAMOTO-OHTA）［6］、基 于ElGamal 签名体制［7］等协议，通过盲签名技术对选民选票签名，存在依赖选举管理机构的公正性、选票碰撞、选举过程操作繁琐、协议效率低等问题。基于混合网络的方案算法复杂，实现困难［8］。针对现有方案存在的投票效率低、可能存在内部欺诈、依赖可信第三方等问题和电子选举主要的两个矛盾点，结合区块链公开透明、不可篡改、集体维护等特性，本文提出了基于区块链的去中心化电子选举方案。选民身份管理设计基于非交互式零知识证明算法zk-SNARKs（zero-knowledge Succinct Noninteractive ARgument of Knowledges）［9］和区块链架构，既保证了选举的匿名性又保证了公开可验证性；选票隐私保护设计基于Paillier 公钥密码体制；通过以太坊智能合约实现选举投票和计票流程自动化，去中心化。

1 预备知识

1.1 以太坊与智能合约

以太坊（Ethereum）是一个基于区块链技术的，可创建、使用智能合约（Smart Contract）和去中心化应用（Decentralized Application，DApp）的开源平台［10］。智能合约是以太坊网络上运行的程序，是一种由事件驱动的，具有具体状态的代码合约和算法合约。智能合约的代码编译后生成的字节码可以在以太坊客户端和节点运行。以太坊平台对底层区块链技术进行了封装，让区块链应用开发者可以直接基于以太坊平台进行开发，只专注于开发应用本身逻辑的智能合约，这样可以大幅度降低开发难度和成本。智能合约适用于对信任、安全和持久性要求较高的应用场景，例如数字货币、数字资产、投票、保险、金融应用、预测市场、产权所有权管理、物联网、点对点交易等。

1.2 零知识证明

零知识证明（Zero-Knowledge Proof）由Goldwasser 等［11］在20世纪80年代初提出，证明者能够在不向验证者提供任何有用的信息的情况下，使验证者相信某个论断是正确的。Goldwasser 等［11］提出的是交互式零知识证明，需要证明者和验证者进行多轮通信证明，对于复杂问题证明效率较低。De Santis等［12］首次提出了非交互零知识证明的概念，证明者只需要按照协议向验证者发送一次消息就可以让验证者以高概率确信一个论断是正确的。最初的非交互式零知识证明系统的效率是非常低，难以应用于实际问题。后续研究证明对于所有的NP语言都存在对应的非交互式零知识证明［13］，研究者们通常将非交互式零知识问题规约到NP 问题上。非交互式零知识证明已被广泛应用于当今的密码体制中。

区块链中每一笔交易的共识验证过程都涉及区块链网络的每一个节点，采用交互式零知识证明开销过大，所以在区块链系统中更适合采用非交互式零知识证明。zk-SNARKs是典型的非交互式零知识证明协议，通过同态隐藏、多项式盲估、匹诺曹协议、椭圆曲线配对等技术，实现了证明者只需要提供的短小的零知识证明字符串proof 就可以完成简洁、高效的证明过程。目前匿名性较好的密码学货币Zerocash［9］就是利用zk-SNARKs 实现交易信息隐私保护。Zerocash中隐私交易信息可以在区块链上完全加密，在加密的情况下仍然可以通过zk-SNARKs证明在该交易在共识规则下的有效性。

1.3 Pailier公钥密码体制

Paillier 算法是一种具有语义安全性，是基于复合剩余类的困难问题的公钥密码体制，该加密算法满足加法同态性和混合乘法同态性，其中加法同态性适用于电子选举系统的选票加密［14］。加法同态指的是通过密文E(X)和E(Y)可计算获得E(X+Y)，解密后可得到X+Y。

Paillier 密钥生成 随机且彼此独立地选择两个大质数p和q，且满足gcd(p×q，(p-1) ×(q-1))=1，gcd 表示最大公约数，计算n=p×q和λ=lcm(p-1，q-1)，lcm 表示最小公倍数。选择随机整数g∈G，G为模n2的乘法群，并且满足μ=(L(gλmodn2))-1modn，其中定义函数L(x)=(x-1)/n。Paillier算法公钥为(n，g)，私钥为(λ，μ)。

Paillier 加密 设m(0 ≤m＜n)为需要加密的信息，选择加密随机数r，r需满足0 ＜r＜n和r∈G，确保gcd(r，n)=1。加密算法EP(m)=gm×rnmodn2，分别对明文m1 和m2 进行加 密，得到对应密文为c1=gm1×rnmodn2和c2=gm2×rnmodn2。密文性质有c1×c2=g(m1+m2)×r2nmodn2=EP(m1+m2)，所以Paillier算法具有加法同态性［14］。

2 去中心化电子选举方案

2.1 方案设计

在本电子选举方案中，参与者如下：

选举发起方 发起选举，初始化选举信息。

线下认证中心（由选举发起方指定） 选举方在注册阶段设置线下验证点，对选民的身份进行验证。

选民 用V1，V2，…，Vn表示。

候选人 一场选举中有多个候选人，对应的候选人用C1，C2，…，Cm表示。

选举初始化阶段，选举发起方初始化选举信息，部署选举智能合约至区块链；选举注册阶段，选民在线下认证中心认证、注册获得投票资格；选举投票阶段，选民通过zk-SNARKs零知识证明算法生成身份证明proofV和选票合法性证明proofB，通过Paillier 算法加密选票，将零知识证明和加密选票发送至区块链；选举计票阶段，智能合约自动调用计票算法，获取区块链上的加密选票，利用Paillier 算法加法同态实现加密计票。整个选举过程数据经国密算法SM2椭圆曲线公钥密码算法［15］、SM3密码杂凑算法［16］处理后公开写入区块链，任何参与者都可以验证投票数据和选举结果。

2.2 基于zk-SNARKs算法选民身份隐藏方案

选民身份管理是电子选举的一大难题，在选举过程中为保证选民身份合法性，需要对选民身份进行有效的认证，但在选举过程中又要需要保证匿名性。针对这个问题，通过区块链架构和zk-SNARKs非交互式零知识证明实现选举匿名性和选民身份合法性验证。投票阶段，通过zk-SNARKs 生成选民身份证明proofV，将proofV和加密选票一同写入区块链；计票阶段，智能合约通过调用验证算法验证proofV间接验证选民身份的合法性。区块链的数据是公开透明的，任何人都可以对区块链上的proofV进行验证；区块链具有一定的匿名性，在区块链实现一次身份隐藏的基础上再通过zk-SNARKs实现二次身份隐藏；基于zk-SNARKs 非交互式特性，一次生成证明proofV，无需多次交互，保证选举效率。

由于zk-SNARKs 不能直接应用于任意问题，必须有可量化的输入，因此需要将实际问题转换成zk-SNARKs 可处理的数学描述模型：首先将需要证明的问题约化为指定的NP 问题，实现基于算术电路的NP 问题的证明和验证；然后再通过多项式盲验证、同态隐藏、匹诺曹协议等技术生成零知识证明字符串proof；最终生成的proof基于多项式等式的抽样验证只需要O（1）的验证代价，验证更为高效、简洁。

zk-SNARKs身份证明算法生成proofV过程如下［9，17］：

1）算术逻辑方程验证转化为算术电路验证。

选民需要在不暴露i的具体数值情况下证明自己是合法选民V1，V2，…，Vn中的一员Vi，算术逻辑方程可表示为：

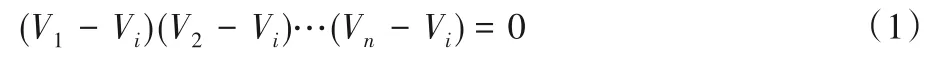
式（1）的门电路可表示为方程组（2）：

将算术方程转化为算术电路，首先将方程分解为加法、乘法组成的最小操作，然后增加中间变量，把复杂的计算方程转化为简单的门电路表示，最终门电路的输出结果与原表达式等价。

其中sys1，sys2，…，sysm是算术电路设计新增的中间变量，out是整个电路的输出，等价于方程的计算结果。该方程的电路表示如图1所示。

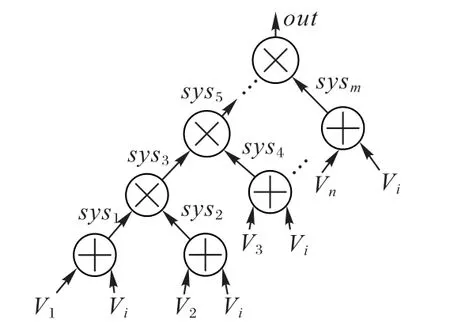
图1 选民身份证明算术电路Fig.1 Arithmetic circuit of voter identification

2）算术电路验证转化为向量验证R1CS（Rank-1 Constraint System）［18］。

将每一个门电路表示为等价的向量点积形式，这个过程称为R1CS，就是将门电路转化成向量的表达方式。首先用一组向量定义算术电路中的所有的变量。上述电路可表示为：one代表常量变量1，V1，V2，…，Vn，Vi代表输入，sys1，sys2，…，sysm代表中间门电路的输出，out代表整体电路输出。则定义s如下：

然后对于每个门电路，存在一组向量(a，b，c)，使得s⋅a*s⋅b-s⋅c=0 成 立。例如门电路sys1=(V1-Vi)，存在向量组：

a=[1，0，…，0，0，0，…，0]，s⋅a结果为one；

b=[0，1，…，0，-1，0，…，0]，s⋅b结果为V1-Vi；

c=[0，0，…，0，0，1，…，0]，s⋅c结果为sys1；

代入s⋅a*s⋅b-s⋅c=0，可计算得到：one*(V1-Vi)-sys1=0，等价于sys1=(V1-Vi)。以此类推，可将所有门电路转化成向量表达式s⋅a*s⋅b-s⋅c=0，获得每个门电路对应的向量组(a，b，c)。

3）向量验证R1CS 转化为QAP（Quadratic Assignment Problems）［19］多项式验证。

本文方案选择将选民身份验证问题归约的NP 问题为二次算数问题QAP，证明QAP 多项式成立就是证明选民身份合法性。QAP 指的是有一系列多项式和一个目标多项式，存在多项式的组合能整除目标多项式。

已知w个门电路都对应存在向量组(a，b，c)，将a，b，c中每个系数看成一个多项式的结果，例如每个门电路对应的向量a的系数作为一个多项式的解，可以反推出多项式a(x)=[f0(x)，f1(x)，…，fk(x)]：对于门电路1，已知解f0(1)，以此类推f0(2)，f0(3)，…，f0(w)都是已知值，可以通过拉格朗日插值法反推出多项式f0(x)，当向量比较大时，可以通过快速傅里叶变化进行优化。同理可以算出f1(x)，f2(x)，…，fk(x)。最终，转化完成后可获得三个多项式数组a(x)，b(x)，c(x)。

定义多项式P(x)=s⋅a(x)*s⋅b(x)-s⋅c(x)，x∈(1，2，…，w)，w是门的数量。已知每个门电路对应的向量组都满足s⋅a*s⋅b-s⋅c=0，则当x取1 至w任意值，都有P(x)=0。根据多项式特性，若P(a)=0，则(x-a)可以整除P(x)，以此类推，P(x)可以被(x-1)(x-2)…(x-w)整除，即满足QAP 定义，存在H(x)=0 使得T(x)=(x-1)(x-2)…(x-w)目标多项式可以整除多项式组合P(x)，生成QAP方程：

s⋅a(x)*s⋅b(x)-s⋅c(x)=T(x)*H(x) （3）

将验证计算方程式（1）转化为验证QAP 方程式（3）过程中的向量s是证明者独有，也只有正确的s才能使方程成立，且在转化过程中插入的混淆值与计算方程的逻辑没有任何关系，QAP多项式的验证不等于原方程的验证，而是原方程的验证包含在QAP 方程的验证里，那么验证QAP 方程等于验证原方程。zk-SNARKs 算法通过抽样实现简洁验证，并不需要验证所有的x，x∈(1，2，…，w)，只需要随机抽查任意一个点验证即可，所以算法验证速度快。

4）zk-SNARKs零知识证明。

验证方程为式（3），为了方便表示，定义A(x)=s⋅a(x)，B(x)=s⋅b(x)，C(x)=s⋅c(x)，则方程表示可为A(x)*B(x)-C(x)=T(x)*H(x)。

椭圆曲线配对［20］证明过程采用椭圆曲线加密算法E(x)=gx，g为生成元。已知椭圆曲线满足加法同态，在验证方程A(x)*B(x)-C(x)=T(x)*H(x)时涉及乘法，可以通过椭圆曲线配对实现计算层面的乘法同态。已知配对函数定义如下：e(gx，gy)=e(g，g)xy，对于明文m1 和m2，对应密文为E(m1)，(m2)，存在等式：

椭圆曲线α对［20］zk-SNARKs 零知识证明利用了α对的性质实现多项式盲验证。椭圆曲线的α对指的是椭圆曲线上满足y=α*x的一对值(x，y)，利用α对的性质，可设计如下证明过程以满足在不暴露隐私信息的情况下让验证相信证明者拥有某个信息：

验证者生成α参数，根据参数生成α对(x，y)，验证者保存参数α，将α对(x，y)发送给证明者。

证明者持有信息β，与验证生成的α对进行计算可获得(x'，y')=(β*x，β*y)。已知y=α*x，利用交换律，则y'=β*y=β*α*x=α*(β*x)=α*x'，根据定义(x'，y')也是一个α对。证明者将(x'，y')发送给验证者。

验证者验证(x'，y')是否是α对，就可以知道证明者是否持有信息β，且验证过程不会暴露证明者拥有的信息β。

公共参考串（Common Reference String，CRS）模型［21］zk-SNARKs 为了实现非交互式零知识证明，采用了公共参考串模型CRS，将验证参数进行处理后公示。若k，α，βa，βb，βc随机参数被泄露，则证明的安全前提将不复存在，所以ZeroCash选择了世界各地6个可信任机构分别生成密钥的一部分，6份密钥拼接在一起生成随机参数k，α，βa，βb，βc和随机参数的公示数据CRS 后便被分别销毁，随机参数k，α，βa，βb，βc也被销毁，由此来保证CRS的安全性。生成proof阶段：

步骤一 验证者确定生成元为g、阶为n的有限群，已知A(x)，B(x)，C(x)多项式的最高阶为d，随机选择有限群中的元素k，和随机参数α，βa，βb，βc计算生成CRS式（5），写入区块链并公布。

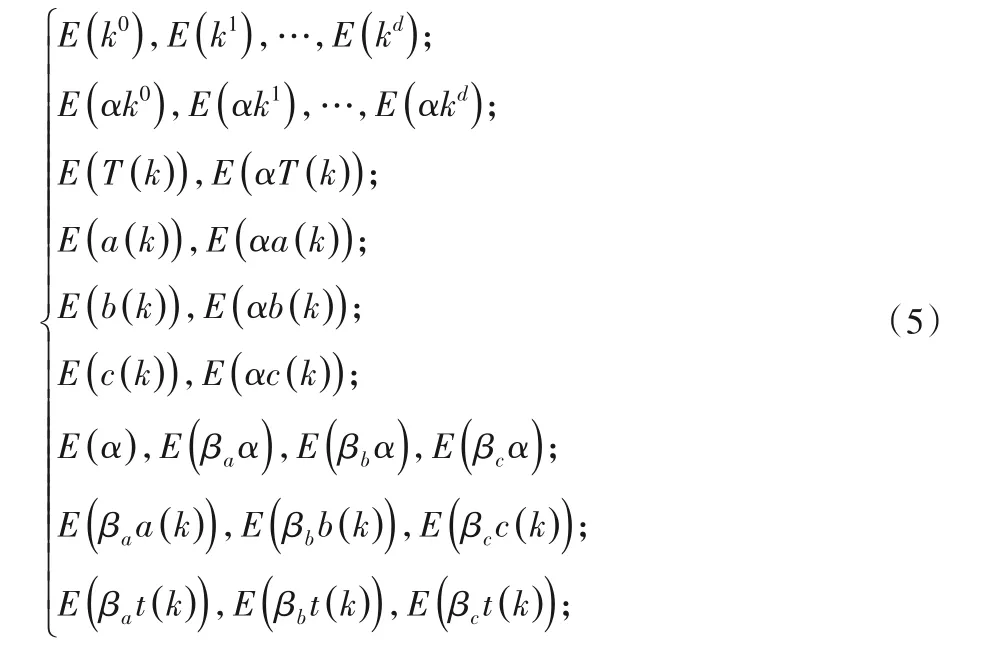
步骤二 证明者利用椭圆曲线的同态性质，读取验证者公布在区块链上的参数CRS可计算生成proofVi如式（6）：

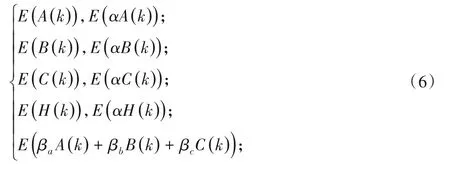
验证proof阶段：

步骤一 验证者仅根据E(A(k))，E(B(k))，E(C(k))是无法确认是由多项式A(x)，B(x)，C(x)的计算生成，利用α对的特性，进行多项式盲验证，验证选民的proofVi是由多项式计算生成。以A(x)为例，验证式（7）和式（8）运算结果相等，则证明E(A(k)) 和E(αA(k)) 是α对，以此类推E(B(k)) 和E(αB(k))，E(C(k))和E(αC(k))，E(H(k))和E(αH(k))是α对，由此证明A(x)，B(x)，C(x)，H(x)都是多项式形式。

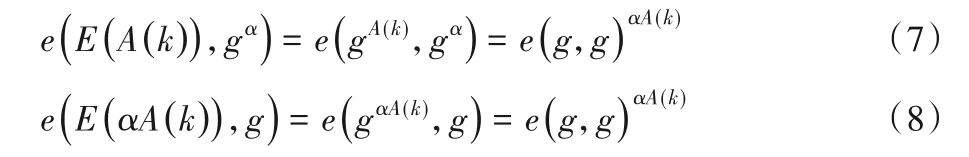
步骤二 整个验证过程中，验证方只随机抽查任意一点k，若验证者无法确认方程（3）是否由s生成，同时证明者知道验证者选择的验证点k，那么证明者就可以任意构造满足验证点的方程，而这个方程可以不由向量s生成。所以验证过程还需要验证A(x)，B(x)，C(x)是由同一个向量s生成，利用多项式特性，只要证明者给出A(x)，B(x)，C(x)的线性组合，则能证明A(x)，B(x)，C(x)从同一组参数s生成，验证式（9）和式（10）相等，则证明βa A(k)+βbB(k)+βcC(k)为线性组合。

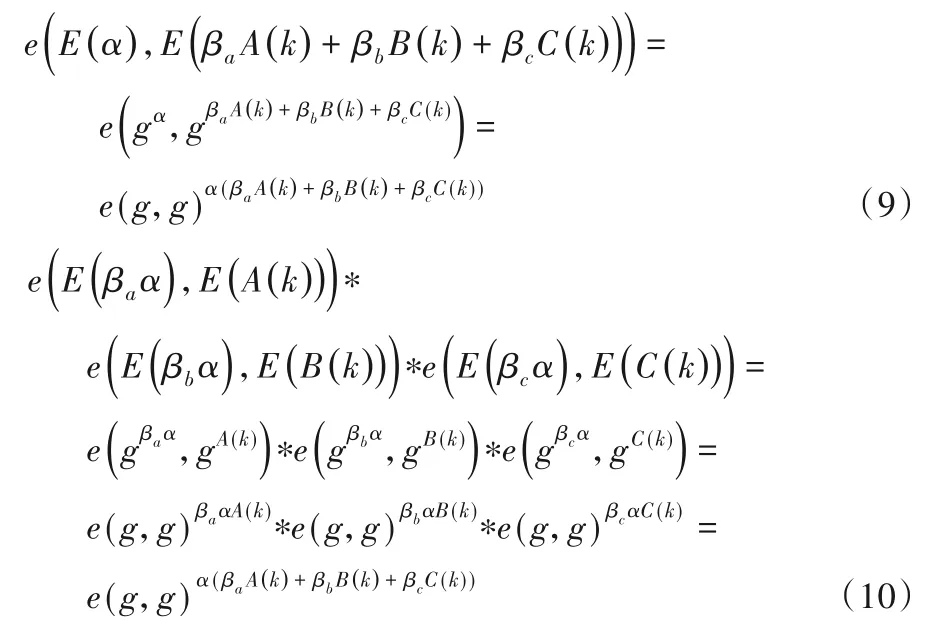
步骤三 通过步骤一和步骤二保证验证数据的合法性，然后验证式（11）和式（12）若相等，则证明A(x)*B(x)=T(x)*H(x)+C(x)，即证明方程A(x)*B(x)-C(x)=T(x)*H(x)成立。

2.3 基于Paillier算法的选票加密方案

针对既要保证选票信息的隐私保密要求，又要保证选举结果的公众可验证性，通过区块链架构、zk-SNARKs 算法、Paillier 密码体制选票实现选票加密方案。投票阶段，将Paillier算法加密的选票和zk-SNARKs算法生成选票合法性证明proofB写入区块链；计票阶段，通过以太坊智能合约实现自动计票，利用Paillier 算法加法同态性质计算选举结果。算法实行多次加密选票，一次解密选举结果，既提高了计票效率又实现选票隐私保密；利用加法同态比乘法同态和全同态计算效率更高；选举数据写入区块链，任何人都进行验证，满足公众可验证性。

选票表示为(ViC1，ViC2，…，ViCm)，ViCj指的是第i位选民投给第j位候选人的票数，ViCj∈(0，1)，i∈(1，2，…，n)，j∈(1，2，…，m)。初始化选票阶段，数组每一位为0，投票阶段，选择哪位候选者就将对应的那一位置为1。用于选票加密的Paillier算法的公钥为(g'，n')，私钥为(λ，μ)。对选票进行加密，加密后公开发布至区块链，选民选票加密情况如表1所示。

表1 加密选票Tab.1 Encrypted ballots

则候选人Cj的加密票数由Paillier 算法加法同态计算得到：使用私钥(λ，μ)进行解密即可获得候选人Cj的总票数：以此类推可计算出所有候选者的票数(t1，t2，…，tm)。

由于选票加密后无法验证选票具体数值，也就无法直接验证选票是否合法（最多只能有一位置为1，其余位全为0），将选票合法性验证问题归约为zk-SNARKs证明。选民需要在不暴露选票(ViC1，ViC2，…，ViCm)的情况下证明选票合法，则逻辑算术表达式为ViC1+ViC2+…+ViCm=0 或ViC1+ViC2+…+ViCm=1，转化为算术电路如图2。

图2 选票合法性证明算术电路Fig.2 Arithmetic circuit of proof of ballot legality

若选民没有选择候选人，则电路out=0，否则out=1。两种不同情况对应不同的out，该电路可表示为：one代表常量变量1，(ViC1，ViC2，…，ViCm)代表输入，sys1，sys2，…，sysv代表中间门电路的输出，out代表整体电路输出。则定义s如下：

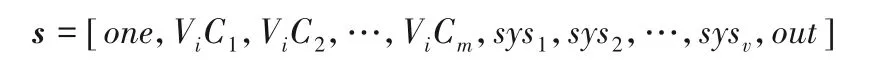
后续根据s计算每个门电路对应的向量组(a，b，c)，转化为向量验证和再转化为QAP 多项验证与选民身份证明s生成过程相同，最终可生成选票合法性证明。

2.4 去中心化电子选举方案流程

整体选举流程如图3所示。

1）选举系统初始化阶段。

选举发起方登录以太坊账号：

初始化选举基础信息：选举名称、选举起止时间等；

初始化用于选票加密的Paillier公私钥：公钥为(g'，n')，私钥为(λ，μ)；

初始化用于选票序列号加密的SM2 公私钥：公钥为P0，私钥为d0；

初始化投票智能合约：候选人名单，C(C1，C2，…，Cm)部署投票智能合约至区块链。

图3 选举流程Fig.3 Election flow

2）选民注册阶段。

选民需要在线下官方机构认证是否是此次选举的合法选民。认证通过后，利用物理可信通道为选民进行注册；

生成选民的SM2 公私钥对(di，Pi)，随机生成唯一选票序列号Ni；

调用SM3算法，对选民身份信息进行加盐哈希处理，生成Esm3(Vi，Salti)，调用智能合约存储至区块链合法选民名单V=(Esm3(V1，Salt1)，Esm3(V2，Salt2)，…，Esm3(Vi，Salti))；

调用SM3 算法，对选票序列号进行哈希处理Esm3(Ni)，调用智能合约存储至区块链合法选票列表N=(Esm3(N1)，Esm3(N2)，…，Esm3(Ni))；

调用SM2 加密算法对Salti进行加密处理Esm2(Pi，Salti)，调用智能合约存储至区块链加盐加密随机参数列表S=(Esm2(P1，Salt1)，Esm2(P2，Salt2)，…，Esm2(Pi，Salti))；

选民自行保管身份信息Vi，私钥di和选票序列号Ni。

注册完毕后，区块链上存储的信息为：

调用zk-SNARKs算法生成后续零知识证明需要的公示参数CRS，写入区块链公示。

3）投票阶段。

选民在终端使用以太坊账号登录。

选民读取存储在区块链上的S，获取对应的Esm2(Pi，Salti)，通过SM2 解密算法获得处理身份信息的Salti：Dsm2(di，Esm2(Pi，Salti))。

选民调用SM3 哈希算法计算得到Esm3(Vi，Salti)，读取存储在区块链上的选民身份信息集合V，调用基于zk-SNARKs选民身份证明算法生成证明字符串proofVi：证明Esm3(Vi，Salti)属于选民集合V。

选民选择对应的候选人Cj，然后生成选票Balloti=(ViC1，…，ViCj，…，ViCm)，如：(0，…，1，…，0)；调用基于zk-SNARKs 选票合法性证明算法生成proofBi，证明选票合法；调用基于Paillier 加密体制的选票加密算法对选票进行加密获得EP(g'，n'，Balloti)；调用SM2 加密算法对选票序列号进行加密获得Esm2(P0，Ni)。

选民将选票信息块Mi发布至区块链即完成投票环节：Mi=(Ep(g'，n'，Balloti)，proofBi，proofVi，Esm2(P0，Ni))。

投票结束，所有选票信息块为M=(M1，M2，…，Mn)。

4）计票阶段。

整个计票流程写入智能合约，当计票环节开始时，自动调用智能合约进行以下流程：获取区块链上所有选票信息块列表M，通过zk-SNARKs 验证算法验证每张选票对应证明信息proofBi、proofVi是否合法 ；通 过 SM2 算法解密Dsm2(d0，Esm2(P0，Ni))获得Ni，验证Esm3(Ni)是否属于N；若两项验证都通过即证明该张选票合法，Ni只能使用一次，证明该张选票合法后，对应的Esm3(Ni)失效。

利用Paillier 算法加法同态性质计算获得候选人(C1，C2，…，Cm)的票数(t1，t2，…，tm)，公布选举结果。

选举结束。

3 实验与结果分析

本文采用以太坊Rinkeby 测试链作为去中心化数据库，Web 端通过Web3j接口与链上智能合约进行交互。实验条件为：64 位操作系统Windows10，内存为16 GB，CPU 为Intel Core i5-7300HQ 2.5 GHz。实验目的：1）验证该去中心化电子选举方案的可行性；2）测试在不同选举规模下选民身份证明算法效率以及计票效率。实验设定选举参数为5 位候选人，分别测试不同选民数量零知识证明proofV生成和验证平均耗时，以及选举结果计算耗时（每张选票平均耗时）。实验过程中，选举执行流程按照智能合约的设定执行，实现无需可信第三方计票机构完成计票流程。实验结果表明，随着选举规模的扩大，选民身份证明的生成与验证耗时、选举结果计算耗时增加，该方案适用于小规模选举应用场景。测试结果如图4所示。

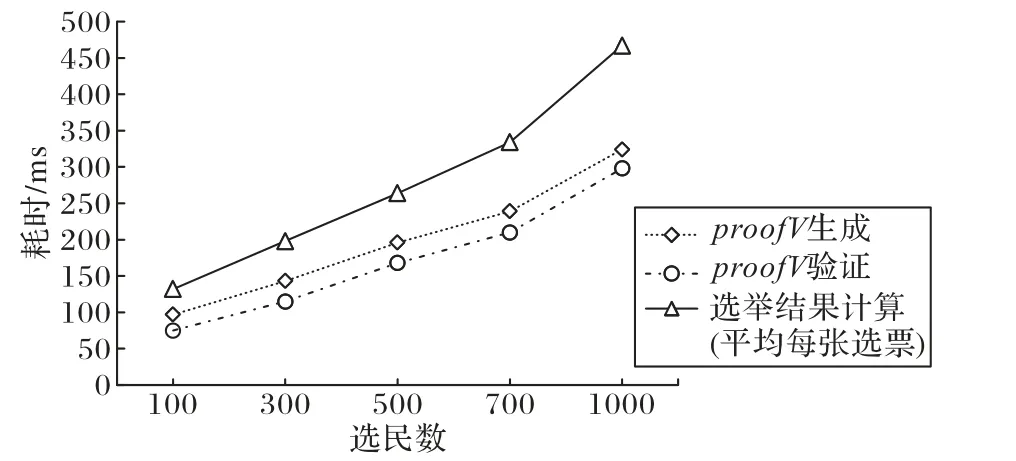
图4 不同选民数量各环节耗时比较Fig.4 Time comparison of different stages with differentnumber of voters

匿名性 区块链具有一定匿名性，所有用户都通过以太坊账户地址进行交易，对选民身份进行了第一次隐藏；基于zk-SNARKs 实现的身份隐藏算法生成proofV对身份信息Vi进行二次隐藏。攻击者无法通过写入区块链的身份证明proofV追踪具体的选民。选民在不暴露身份信息的情况下实现合法性证明，实现了选举的匿名性。

选票的隐私性 该选举方案中通过Paillier 密码体制加密选票，通过zk-SNARKs 算法生成选票合法性零知识证明proofB，攻击者无法通过proofB获取任何信息。且相较于基于乘法同态、全同态选举方案，Paillier 算法加法同态计算效率更高。

健壮性 非法选民不能破坏系统的正常运行。测试环节中，针对投票、计票阶段进行攻击测试。构造非法选民Vh(h∉(1，2，…，n))写入非法投票信息块Mh，计票环节验证非法身份证明proofVh无法通过，非法选票被丢弃。只有合法有效的投票才能被正确地统计。选举数据存储在区块链分布式数据库中，单一节点损坏不影响系统正常运行。

可验证性 整个选举过程的数据都公开写入区块链，任何投票者都可以检验自己的选票是否已经被正确计入，也可以验证区块链上任意一张选票的投票信息块Mi的proofV、proofB的合法性，实现了公开可验证。

4 结语

本文针对电子选举主要的两个矛盾点，设计了基于区块链的去中心化安全电子选举方案。通过零知识证明算法zk-SNARKs 实现了选民身份隐藏，通过Paillier 算法实现了选票信息隐藏，切断了公布的选票信息与每张选票具体持有选民这二者之间的直接联系；通过智能合约实现自动计票，无需可信第三方计票机构。但是实验表明由于零知识证明算法和同态加密算法限制，随着选民规模的扩大，验证与计算的速度降低，仅适用于小规模选举。如何实现去中心化、高效率的大规模选举是今后的研究方向，可以对零知识身份证明算法和同态计算进行进一步研究。