社交网络中对立影响最大化算法

杨书新，梁 文，朱凯丽

（江西理工大学信息工程学院，江西赣州 341000）

（*通信作者电子邮箱jhcpl05@163.com）

0 引言

社交网络用户间的关系是多样化的，或协作配合、或对立排斥或动态博弈，传统单源信息的影响传播研究无法描述其复杂性，因此产生了多源信息影响传播的研究。多源信息影响最大化也称之为竞争影响最大化。谣言阻碍、捆绑销售、党派博弈、病毒营销、游戏竞赛的规则模拟均属于多源信息影响最大化的研究问题［1-3］。现有工作主要依靠经典独立级联（Independent Cascade，IC）模型和线性阈值（Linear Threshold，LT）模型开展研究，部分用于求解竞争影响最大化问题的算法仅适用于特定结构的数据，尚缺乏普适性。针对上述不足，本文扩展热量传播模型为多源热量传播模型，研究对立影响最大化问题。

1 相关工作

2007 年，Bharathi 等［4］首次给出竞争影响最大化（Competitive Influence Maximization）问题的定义：已知种子集SA分布的情况下，选拔种子集SB，使SB的影响传播效果最大化，其中SA和SB代表不同信息源。竞争影响最大化的相关研究产生了许多具有代表性的成果，本文围绕竞争影响传播模型、竞争影响传播问题的优化算法两方面介绍国内外研究现状。关于竞争传播模型，已有相关工作主要针对单源信息的独立级联（IC）模型和线性阈值（LT）模型加以扩展。基于IC模型，文献［5-6］提出了基于IC 模型的多实体竞争（Multi-Campaign IC）模型、波扩散（Wave Propagation）模型及基于距离的（Distance-based）多源信息传播模型。Borodin等［7］率先利用LT 模型研究竞争影响最大化问题，设计了权重竞争阈值（Weight Competitive LT）模型、分隔竞争阈值（Separate Competitive LT）模型。He 等［8］首次定 义了竞争线性 阈值（Competitive LT）模型。

关于竞争影响最大化问题的优化算法，相关工作已取得了积极进展。文献［4］提出的FPTAS（Fully Polynomial-Time Approximation Scheme）在理论上具有63%的下界保证。针对竞争影响最大化问题，He 等［8］提出了适用于有向无环图的CLDAG（Competitive Local Directed Acyclic Graph）算法。Zhu等［9］研究了基于位置感知的影响阻碍最大化（Location-aware Influence Blocking Maximization，LIBM）问题，利用位置数据划分区域，设计了LIBM-H和LIBM-C两种启发式算法，实验表明两种算法均能有效求解竞争最大化问题。文献［4，9］的算法仅适用于树型数据结构。Pham 等［10］研究了回避多余用户（unwanted users）的竞争影响最大化问题，多余用户是非预期内被影响的特定群体。文献［10］基于竞争阈值模型证明了该问题是NP-Complete问题，设计了一种启发式方法并在真实数据集中验证了有效性。

本文考虑信息对立式竞争影响传播的形式。对立影响传播是指多源信息传播中，成功影响个体的信息是唯一的。对立信息的影响传播可以概括许多生活化的场景。例如社交网络中用户对舆论事件正面及负面观点往往是对立的。或是通过社交网络的广告影响，用户确定购买某个品牌商品后，短期内不会考虑再购买同类别其他品牌商品。针对信息的对立竞争形式，本文扩展单源热量传播模型为多源热量传播模型，设计了预选式贪心算法，并在编程爬取的大规模社会网络数据集中验证其有效性。

2 问题及模型的定义

2.1 对立影响最大化问题的定义

给定社交网络G=（V，E）与信息传播模型，其中：V表示由网络节点构成的集合，E表示网络节点间边的集。已知种子集SA⊆V的分布情况，选拔由k个节点构成的种子集SB⊆V且SB⊆VSA，使SB的影响收益σ(SB，SA)最大化，其中SA和SB代表对立的信息源。对立影响最大化（Reverse Influence Maximization）问题的形式化表达为：

当SA=∅时，传统单源信息传播的影响最大化问题即为对立影响最大化问题的特例。σ(SB，SA)是集合V的子模函数，因此仍具有子模特性。以σ(SB，SA)为目标函数，贪心近似（Greedy Approximation）算法经过有限次的迭代计算，可以得到保证下界的近似最优种子集SB，即≥(1-1/e)σ(SB，SA)。

2.2 多源热量传播模型的推导

根据物理经验，热量总是自高处向低处转移以达到均衡。社交网络的信息传播过程与此相似，向外传播影响的个体总是最先被激活的种子。同样，设具有不同标记的热量与不同的信息是对应的，则单源信息的热量传播（Heat Diffusion，HD）模型［11］可被扩展为多源信息热量传播（Multi-Source HD，MSHD）模型。该模型可用于模拟对立信息的影响传播，解决对立影响最大化问题。下面给出MSHD模型的推导过程。

给定有向社交网络G=（V，E），G中的任意一个节点vi在传播初始时刻t=0时，其热量参数记为hi(0)；t≥1时，vi的热量值记为hi(t)。采用h(ξε，t)记录G中全部节点在t时刻的热值，向量长度为节点总数n(n=|V|)，其表达式为：

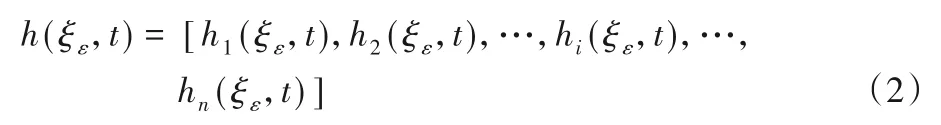
其中，ξε(ε＞2，ε∈Z+)对应的是ε个信息源的不同激活状态。热量总是沿有向边，自高向低转移。以节点vi为例，若节点vi与节点vj间存在有向边，即evj，vi∈E。根据节点有向边的不同方向，将vj与vi的热量转移分两种情况讨论。

考虑情况一，若节点vj指向节点vi，此时节点vi热值为0，或节点vj和vi的激活态相同且vj热值高于vi。自t时刻开始，经过一段时间Δt后，热量从vj向vi转移的量为(α⋅hj(t)⋅Δt)/dj，dj表示节点vi的出度邻居数量，导热系数（Thermal Conductivity）α表示信息的传播能力。在Δt的时间长度内，节点vi收到的总热量记为Ghi(t，Δt)。

考虑情况二，若节点vi指向节点vj，此时节点vi和vj的激活态相同且vi热值高于vj。自t时刻开始，经过一段时间Δt后，热量自vi向vj转移的量设为Phi(t，Δt)。则节点vi对其前向节点及后继节点的能量转移公式为：

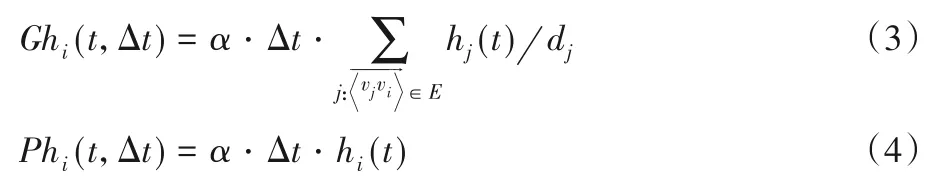
仍以节点vi为例，在t+Δt时刻内，节点vi所转移的热量为应为hi(t+Δt)-hi(t)，其表达函数为：

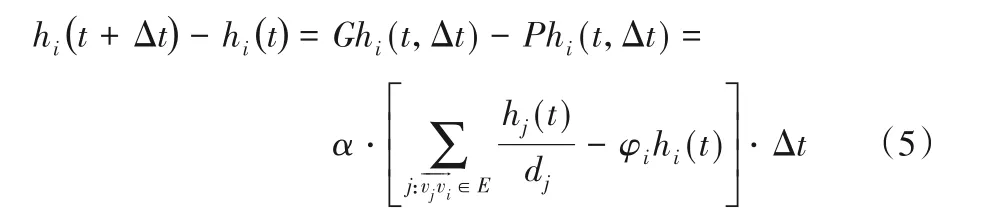
式中，φi是热量输出的标志位，其值只能为0 或1。当φi为0时，表示热量无法发生转移，即节点vi无后继节点（di=0）或节点vi与其邻居的热量标记不同(ξε(i) ≠ξε(j))；当φi值为1时，热量可以发生转移，即节点vi存在后继节点（di＞0）且节点vi与其邻居的热量标记相同(ξε(i)=ξε(j))。根据泰勒公式（Taylor series），整理式（5）得到节点在t时刻的热量表达式为：

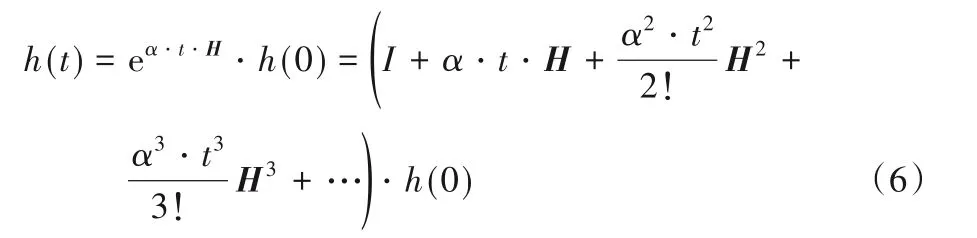
其中：e是自然数，H是图G中节点连接关系的n阶矩阵：

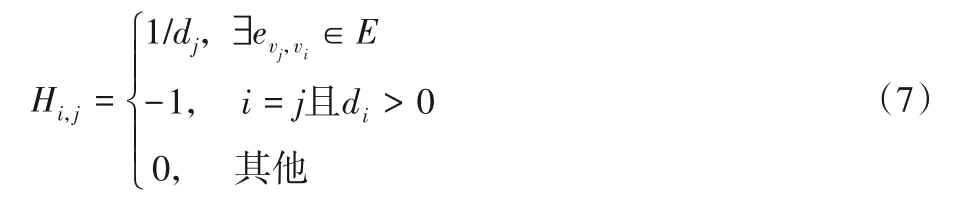
同样，根据节点当前的标记状态、热量值的大小加以相应的调整，MSHD 模型也可适用于无向网络。将MSHD 模型应用至实际问题中，以对立的两个信息源为例即可。

2.3 打破平局规则的设定

传播模型和打破平局规则（tie-breaking rule）［12］是对立信息影响传播机制的核心。打破平局规则用于处理节点被多源对立信息同时影响的状态响应问题。现实社交网络中，个体所接收的信息五花八门，而其最终采纳的信息源总是唯一的。以市场上存在竞争的笔记本电脑品牌为例，用户若锁定某品牌并购买，该用户在短期内不会购买同类别商品。可以认为不同品牌的商品对普通用户的影响是对立传播的。为合理表达上述情境中个体的决策问题，本文设计了一种随机规则（random rule）。该规则设定激活同一个节点的信息源是唯一的，且被激活的过程不可逆，其具体步骤见图1。

以图1（a）的简单网络为例，此时节点u同时面对4股对立的热源，采用随机规则，节点u的状态响应的过程如下：列举由节点u直接邻居构成的序列，如图1（b），将图1（b）的序列乱序排列得到图1（c）。根据图1（c）的排列次序，种子以激活概率p（本文设为0.5）依次尝试激活节点u，首个激活节点u的信息源将作为成功激活节点u的种子。节点u被激活后，不再接受其他状态种子的影响。

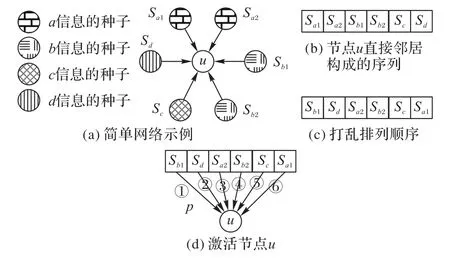
图1 随机规则Fig.1 Random rule

2.4 模型的传播步骤及示例

2.2 和2.3 节完善了MSHD 模型的传播机制，下面给出该模型的传播步骤：初始时刻t=0，对立种子集SA已知，部署种子集SB至网络G中并赋予初始热量。当t＞0时，集合SA和SB中的初始节点参照热量传导公式沿有向边转移热量，当节点预接收的热量不属于同个信息源，采用随机规则处理。重复该过程直至经过有限步长，统计当前热值高于热量阈值的节点，并标记为激活节点。以图2 的简单网络为例，给出MSHD模型的仿真计算过程。

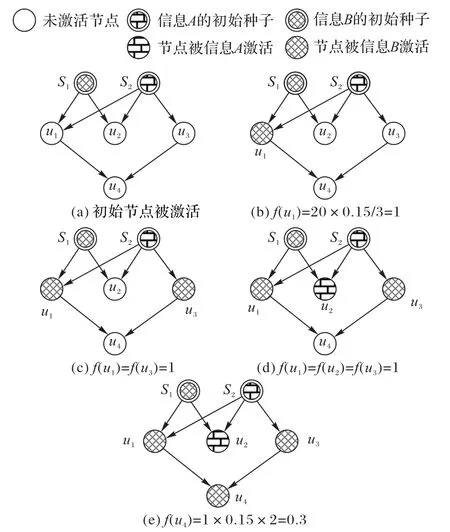
图2 MSHD模型的计算过程Fig.2 Computing process of MSHD model

假定网络中存在A、B两种对立信息源，初始节点的热量值为20，导热系数为0.15，f（）表示节点当前的热量值，节点的热量激活阈值等于0.2。当t=0时，网络中仅有S1、S2作为初始节点被激活；当t=1时，热量开始传导，对立种子S1、S2共同影响节点u1、u2、u3。根据2.3节的随机规则，考虑节点u1、u3被信息B激活以及节点u2被信息A激活的情况（对应图2（b）至图2（d））；当t=2时，节点u4接收节点u1、u3共同传导的热量，根据式（6），f（u4）=0.3。传播结束，根据热量阈值，信息A对应的激活节点数量为2，信息B对应的激活节点数量为4。

3 预选式贪心近似算法

根据2.2 节，热量值和激活阈值是多源热量模型传播机制的重要组成部分，该部分信息可用于统计个体的传播收益，本章基于多源热量模型对个体影响力的评价特性及目标优化函数的子模特性，设计了预选式贪心近似（Pre-Selected Greedy Approximation，PSGA）算法。该算法对网络中的每个节点赋予0～1 随机值，将随机值大于拦截值r、出度值大于平均出度值的节点加入临时种子集S，且该临时集的长度不能大于k。在M次的迭代过程中，根据式（6）和随机规则，统计第m次迭代的临时种子集Sm中全部个体的影响收益，迭代结束后将其收益值降序排列，取Top-k节点作为种子。

对于有向的社会网络图G，选择节点出度及出度均值作为PSGA 算法关键指标的理由如下：在有限的传播步长内，热量和影响总是沿有向路径向外传递和扩散，因此节点的出度值可概括其传播能力。其次，度方法的同一度量值存在若干节点与其对应，众多具有相同度量值的节点被确定为种子时其顺序相对随机，存在高影响力节点被排除的可能。PSGA算法的随机策略可避免该缺陷，并减少计算量。算法1 给出了PSGA算法的运行步骤。

在算法1中，u.degree表示节点u出度值，avgD（G）表示图G中节点的出度均值，I（u）表示节点u的传播收益，SM表示第M次迭代的临时种子集，getSize（）函数用于获取临时种子集Sm的宽度。其中，第2）～7）行含义为：对于每个节点进行判断，将满足条件的节点加入临时种子集，作为种子候选。

算法1 预选式贪心近似算法。

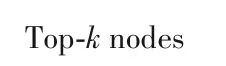
4 仿真结果及分析

4.1 网络数据集

表1列举了仿真实验所需的四组网络数据，n表示网络节点数量，m表示边的数量，＜c＞表示网络的平均聚类系数，type表示网络类型。表1中：p2p-Gnutella08 和CA-HepTH 网络是SNAP的开源数据集，分别表示分布式协议交互网络和维基百科的管理员投票网络。twitter 数据集通过编程爬取自twitter社交平台，记录的是用户间的互粉关系。TecentWeibo 爬取自腾讯微博，该数据记录的是朋友间的关注关系。

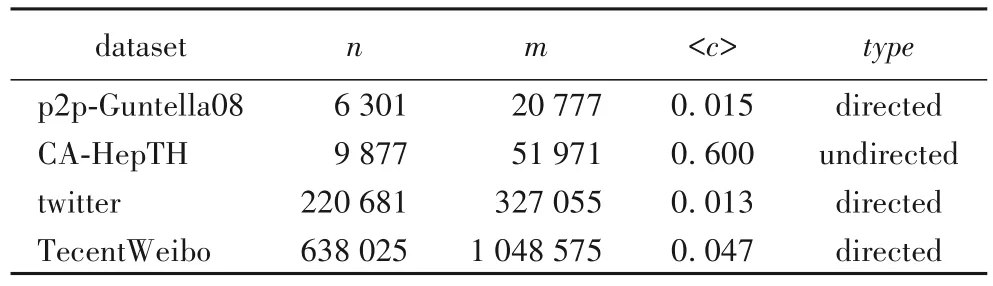
表1 实验网络基本特征Tab.2 Basic characteristic of experimental networks

4.2 仿真实验条件

本节介绍仿真实验的对比算法、算法特点、实验参数和评价方法。

仿真实验采用C++语言编写，在内存为16 GB 的个人工作站上运行。实验选取局部中心性（Local Centrality，LC）［13］、SIR（Susceptible Infected Recovered）评价方法、k-shell［14］方法、基于局部集体影响的自适应排序（Local Collective Influence Rank-Adaptive Recalculation，LCIR-AR）算法［15］、局部三角中心性（Local Triangle Centrality，LTC）方法［16］、密度中心性（Density Centrality，DC）方法［17］同PSGA 算法对比。LC、kshell、LCIR-AR 及LTC 均属于依赖网络拓扑特性的启发式算法，SIR 评价属于模型评价方法。SIR 评价方法利用传染病模型计算个体的影响值F（t），每个节点的F（t）均为重复运行103次的均值。其中，twitter 和TecentWeibo 网络数据因节点数量较多，分别重复运行100 次及50 次。SIR 模型设定传染概率为0.015，传播步长为10，治愈概率为1/k，k为网络节点度的均值。传播步长设定太短会抑制部分节点的传播能力，导致传播停止的时刻提前，传播步长参数对应的值较高，可以反映出节点的真实传播能力。SIR 模型相关参数的设定是复杂网络传播动力学文献较为常见的设置办法，该方法也常用于节点重要性的评估领域，例如本文所对比的文献［13，16］。实验设定LCIR-AR 算法的控制参数为0.3，度量层级为3，根据对比文献［15］的描述，此时该参数对应的实验效果最佳。PSGA算法的拦截值r设为0.85，迭代次数M设为104。

以A、B两种对立信息为例，设100个由随机选拔得到的A种子已知。为了满足实验的公平性，MSHD 模型的传播步长同SIR 评价模型的传播步长均为10。MSHD 模型初始热量值100，激活阈值0.5，导热系数0.15。B信息的种子个数自0 至50 以2 为间隔，逐批投放。其中，B种子仿真收益的计算公式等于B种子收益同A种子收益的差。当信息A的种子集SA和信息B的种子集SB存在相同节点，即SA∩SB≠∅时，采用抛硬币式随机规则处理该冲突。因所采用的冲突处理办法具有随机性，最终仿真收益均为重复运行104次的均值。评价对立影响最大化算法的优劣，从运行时长及影响收益两方面判断。运行时长短，影响收益高，则算法更优。

4.3 仿真结果及分析

图3描述的是7种算法在四组网络数据集的收益表现，其纵坐标影响收益值被归一化处理，横坐标表示种子数量。

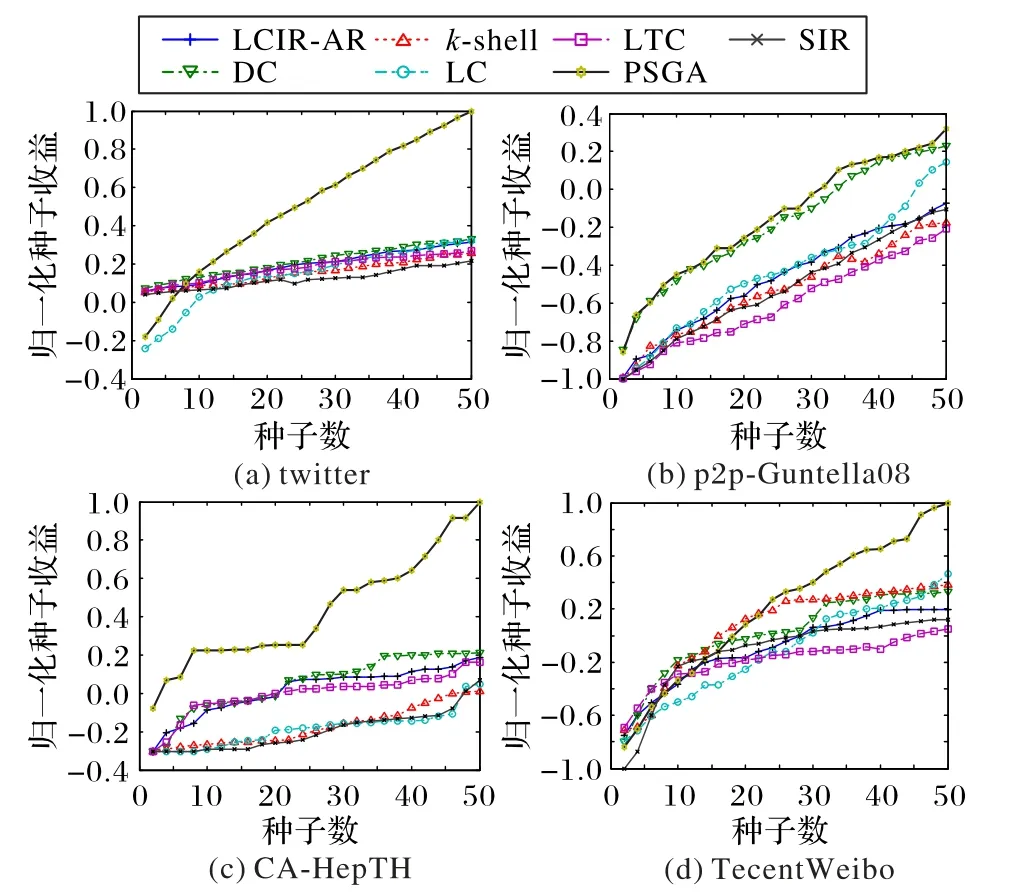
图3 7种算法的仿真收益比较Fig.3 Simulated revenue comparison of seven algorithms

根据图3 仿真结果，PSGA 算法随着种子投放数量的增加，其影响收益涨幅十分明显。twitter 数据集种子数量小于8以及TecentWeibo 数据集种子数量小于14时，PSGA 算法的优势不够明显，但整体上PSGA 所获得的收益最高。尤其是在p2p-Guntella08 和CA-HepTH 数据集中，PSGA 算法表现最优。可以认为，在对立影响最大化问题中，种子投放数量越多，PSGA 算法越能体现出优越性。SIR 模型作为复杂网络度量单体影响力的评价标准，在解决对立影响最大化问题中的表现逊于PSGA 算法。密度中心性（DC）方法在所对比的启发式算法中表现最优，但其整体表现仍无法超过PSGA 算法。LC、LTC、LCIR-AR 及k-shell 方法在四组数据集中的收益排名并不稳定，说明在不同规模和不同类型的网络中，其适用性有限。以k-shell方法对TecentWeibo 网络数据的度量结果为例，k值为57 的个体有759 个，自759 个节点中选拔50 个作为种子，其次序相对随机。因此，k-shell方法度量值区分度不高是其影响收益较低的关键因素。LTC 方法统计节点所处拓扑结构的三元闭包数量，在有向图中其表达的含义为节点经有向路径指向自己的回路数量，在无向图中，其表达含义为节点与紧邻个体的紧密程度。可以认为，针对对立影响最大化问题，三元闭包的统计量无法高效地反映节点潜在的博弈和竞争能力。

为直观表达不同算法的影响收益水平，图4 给出了各方法的平均收益。根据图4 的仿真结果，在四组数据集中，PSGA 算法的平均收益最多，DC算法表现次优，其他算法的表现则不够稳定。

图5 给出了仿真实验每运行104次的平均时间。为统计每个节点的F（t）值，SIR 模型在四个数据集上的运行时间均超过3.5×105s（4 d），TecentWeibo 网络数据的运行时间超过1.8×106s（20 d），其平均时长在图中没有标注。根据图5统计结果，整体上DC 算法的平均运行时间最短，在所对比的启发式算法中，LC 算法的运行时间较长。根据4.2 节对立影响最大化的两项评价指标，PSGA 算法同SIR 评价方法相比，影响收益高、运行时长短，具有优越性。同其他启发式算法相比，PSGA算法虽耗时更久，但平均收益领先于启发式算法。可以认为，PSGA算法能够有效求解对立影响最大化问题。

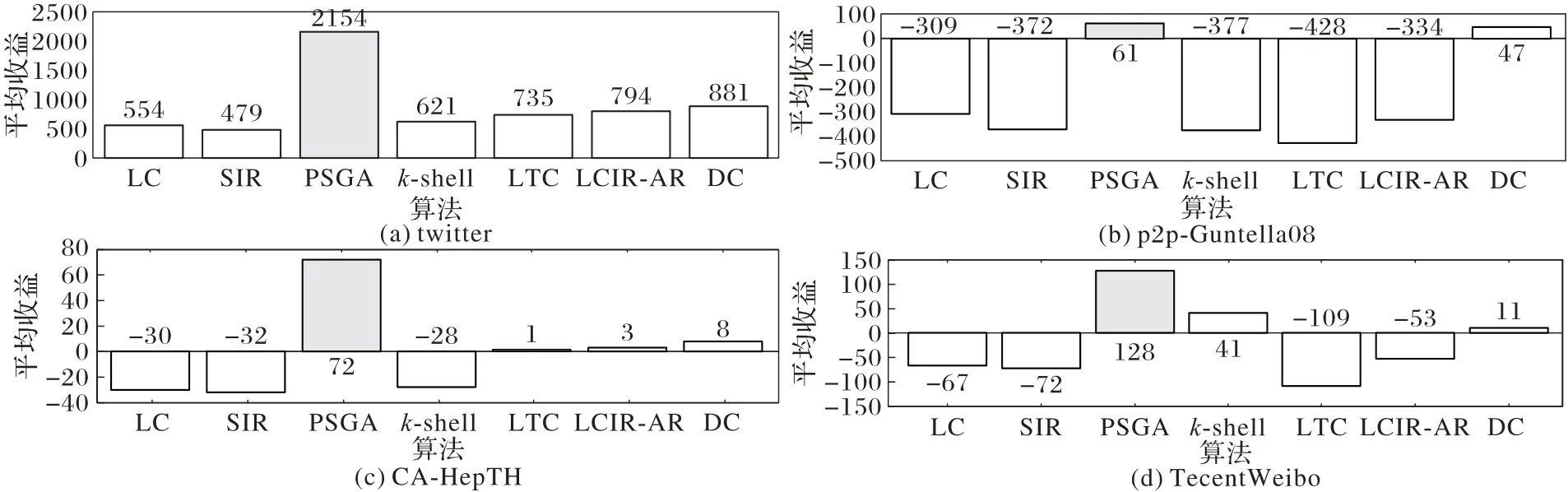
图4 7种算法的平均收益比较Fig.4 Average revenue comparison of seven algorithms

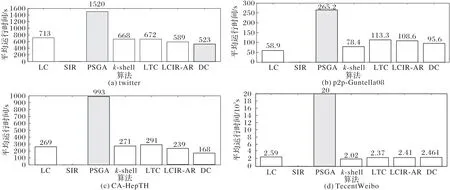
图5 7种算法的运行时间比较Fig.5 Running time comparison of seven algorithms

4.4 种子富集性分析

为进一步分析各算法的仿真收益表现，设计了种子富集性实验，探究各算法所选种子集的特征。种子富集性（richclub）也称富人俱乐部现象，它描述的是关键节点间边的密集情况。种子节点间连接紧密，则不利于影响力的扩散；种子节点间连接稀疏，则有利于初期快速地扩散影响。以图6（a）的简单网络为例，该网络中被对立信息A激活的节点已知。当B种子以图6（b）的方式投放，种子节点相互抱团，处于网络边缘的种子无法对传播起到促进作用。当B种子以图6（c）的方式投放，则有利于初期的影响传播。图6（b）中B信息种子间边的数目为7，图6（c）中B种子间边的数目为0。可以认为种子节点间边的数量能够反映出种子集的富集程度。

根据上述分析，本节设计了种子富集性实验。实验首先读取社交网络图G=（V，E），输入某方法选拔出的k个关键节点，针对E中每条边ei，j∈E作如下判断：若图G中的边ei，j所连接的节点均为关键节点，则对该条边添加标记。最后统计该方法的标记数量。其中，CA-HepTH 网络添加了预处理过程，删掉了个体指向自身的12 条回环边。图7 是种子富集性的实验结果。

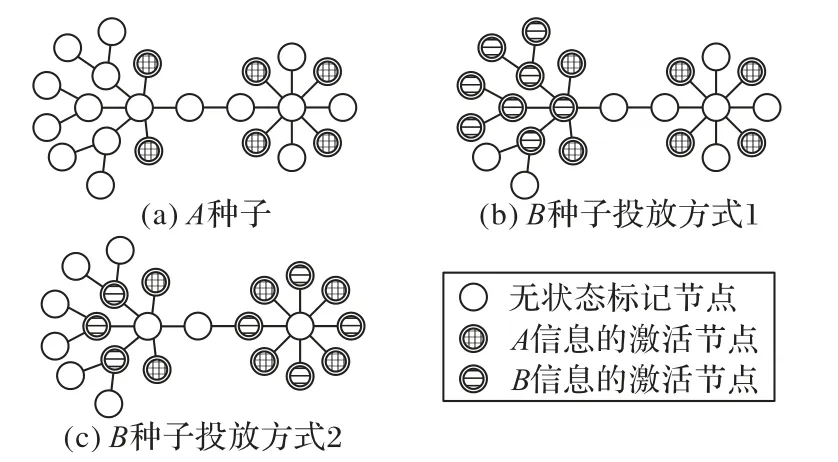
图6 种子富集性示例Fig.6 Diagram of seed enrichment degree

根据图7的实验结果，整体上SIR评价模型的种子富集性最为稀疏，PSGA 算法其次。LC 算法在有向图中的富集性程度高，即种子间的连接较为紧密，在无向图中其富集程度较弱，即种子间的连接较为稀疏，DC、k-shell 和LCIR-AR 算法则与之相反。启发式算法依靠网络局部拓扑特性，SIR 和PSGA依靠各自模型传播机制评价节点的重要性，因此在种子富集性方面具有优势。

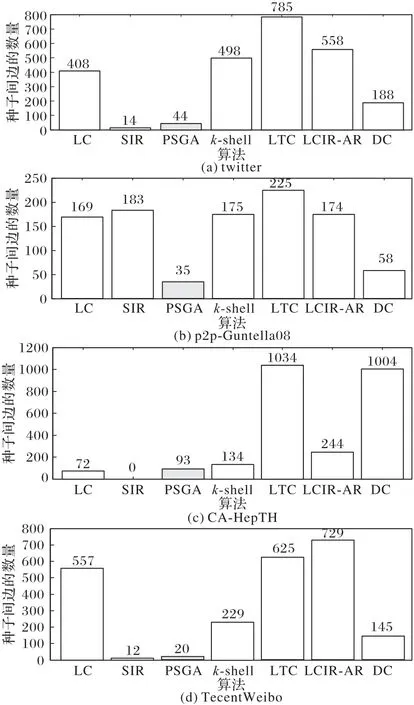
图7 种子富集性实验结果Fig.7 Experimental results of seed enrichment degree

5 结语

针对信息的对立传播情形，本文研究对立信息传播的影响力最大化问题。研究分析了对立信息的传播机制，设计了多源热量传播模型以及用于处理传播冲突的随机处理办法。实验结果表明，本文所设计的PSGA 算法能够有效求解对立影响最大化问题，且在种子富集性的指标上占据优势。然而，PSGA算法存在时间复杂度较高的问题，未来将针对算法运行效率加以改进，使其合理适用于规模较大的社交网络数据集。