利用齐次化处理圆锥曲线问题

袁方程 黄俊峰

(湖北省大冶市第一中学，435100)

解析几何问题因为计算量大,运算复杂,使得很多学生大伤脑筋,甚至望而却步.其中有一类与斜率相关的问题,按照一般思路计算较为繁琐,但如果能利用斜率巧构齐次式,运用类比联想反向推演,寻找与所求问题的内在联系,可使问题简便获解.

一、斜率之和问题

(1)求C的方程;

(2)设直线l不经过点P2且与C相交于A，B两点.若直线P2A与P2B的斜率的和为-1,证明:直线l过定点.

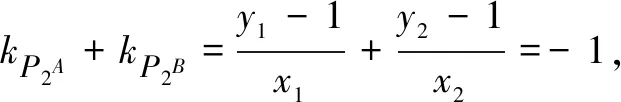
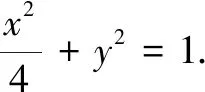
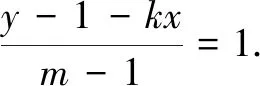
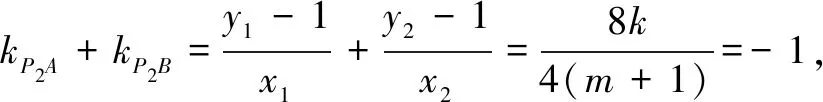
(1)求椭圆C的方程;

(2)E，F是椭圆C上的两个动点,如果直线AE与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.

二、 斜率之积问题

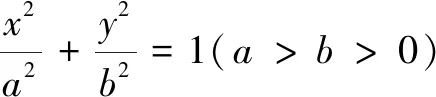
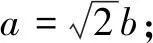
(2)设Q1，Q2为椭圆上的两个动点,OQ1⊥OQ2,过原点O作直线Q1Q2的垂线OD,垂足为D,求点D的轨迹方程.

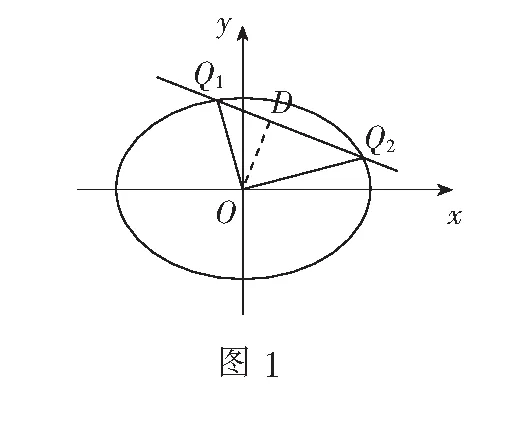
解(1)略.

(2-2b2n2)k2-4mnb2k+1-2m2b2=0.

例3(2011年浙江高考题)已知抛物线

C1:x2=y,圆C2:x2+(y-4)2=1的圆心为点M.

(1)求点M到抛物线C1的准线的距离;

(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A，B两点,若过M，P两点的直线l垂直于AB,求直线l的方程.

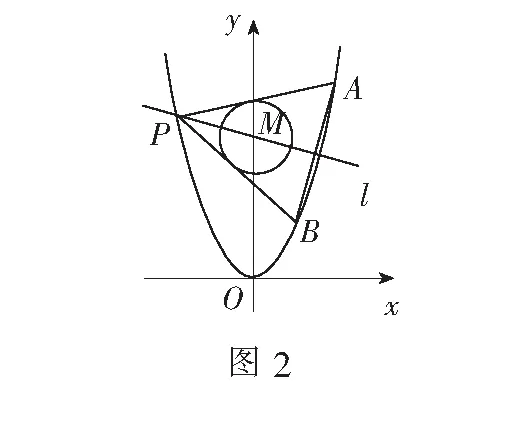
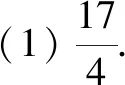
(2)设A(x1,y1)，B(x2,y2)，P(t,t2),其中t≠0,t≠±1,x1≠x2,则切线AP的方程为y=(x1+t)(x-t)+t2,即

(x1+t)x-y-tx1=0.

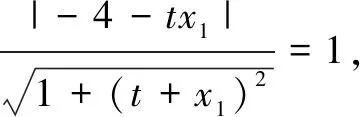
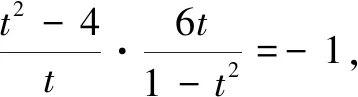
解析几何的同构式方法中，把解析几何大题的关注点从粗放的“联立求解”转移到分析推理上来，从而自然地将几何问题代数化，这本身也是解析几何的精髓所在.通过以上典型例题分析，能让学生多从高考真题中体会其“设而不求”的技巧，可以大大简化运算.