基于卷积神经网络的风电机组轴承机械故障智能诊断方法

史光宇， 徐 健， 杨 强

(1.上海电力大学 电气工程学院，上海 200090； 2.浙江大学 电气工程学院，浙江 杭州 310027)

0 引 言

近年来，随着风电技术不断发展，风力发电快速发展，风能已受全世界高度青睐[1]。全球风能理事会在2019年发布的统计报告显示，2018年全球风电新增装机容量约51.3 GW，累计装机容量突破591 GW，相比去年增长9%。截至2018年中国风力发电累计装机容量已达211.4 GW，占全球累计风电装机容量35.4 %，占比位居第一[2]。

风电机组运维问题日渐突出，维护费占总投入的10%～25%[3]。随着机组运行时间增加，风机叶片、齿轮箱、发电机及其他部件极易发生异常和故障，导致机组运行异常甚至停机[4]。

齿轮箱为风力发电机中重要传动部件，在实际运行中故障率较高，据统计约20%的停机时间是齿轮箱故障造成的[5]。统计数据[6]显示，约76%的故障发生在轴承部件上，齿轮和其他部件的故障率分别仅为17.1%和6.9%。故轴承故障是造成风机齿轮箱失效的主要因素。

目前，用于风电机组故障诊断的信号主要有：振动信号(Vibration)、声发射信号(Acoustic emission)、应变力信号(Strain)、温度信号(Temperature)、油液参数(Oil parameters)、电信号(Electrical signals)等。我国电力系统常用监控和数据采集系统(Supervisory Control and Data Acquisition，SCADA)进行数据采集和监测控制[7]。振动信号是最广泛应用的监测信号，在轴承、齿轮、叶片、传动轴等部件故障诊断中发挥重要作用。因振动信号蕴含内在故障特性，通过信号处理技术能准确有效地识别出故障种类、故障位置、故障严重程度等[8]。

1 风电机组振动信号处理与故障诊断方法

目前，机械振动信号处理常用方法主要分为时域分析、频域分析和时频域分析[9]。

(1)时域分析

时域分析计算多个时域统计指标作为时域特征，并以此为依据进行故障诊断，如均值、绝对平均值、最大值、均方根值、方根幅值等有量纲参数，及峰值指标、裕度指标、脉冲指标、偏度指标和峭度指标等无量纲参数[10]。时域分析简单和直观，但反映的故障信息有限，对于噪声干扰和复杂故障信号处理存在诸多困难。

(2)频域分析

频域分析主要包括幅值谱、功率谱、能量谱、倒频谱、高阶谱和包络谱等[11]。幅值谱是幅值在频域的分布。能量谱也称能量谱密度，是单位频带内信号能量。功率谱为单位频带内信号功率，反映了信号功率随频率变化情况。包络谱可通过对信号做Hilbert变换后取包络信号进行FFT，来剔除不必要的频率干扰而凸显故障特征频率，多用于发现早期故障[12]。频域分析可得丰富而有效的特征信息来实现故障辨识，但仅限于平稳信号分析。

(3)时频域分析

风电机组复杂且运行工况多变，时域分析和频域分析都只能提取单一域信息，而时频分析兼顾时域和频域的特征信息，利于非平稳信号分析。时频分析主要包括短时傅立叶变换(Short-term Fourier Transform, STFT)、小波包变换(Wavelet Packet Transform，WPT)、希尔伯特-黄变换(Hilbert-Huang Transform，HHT)、S变换和魏格纳-威利分布(Wigner-Ville Distribution，WVD)等[13]，它可将一维信号转换为时间和频率关系的二维图像信号，时频图结合灰度直方图、灰度共生矩阵法等纹理特征构造法可用于故障分类识别。局部均值分解(Local Mean Decomposition，LMD)和经验模态分解(Empirical Mode Decomposition，EMD)等自适应非平稳信号时频分析法也在风机齿轮和轴承故障诊断中被广泛应用[14，15]。

近年来，智能诊断方法在机械故障诊断中受到了广泛的关注。故障智能诊断本质是模式识别，正常运行与各种故障状态都可看作特定模式，可根据提取的特征进行分类识别。在智能诊断方法中，主成分分析(PCA)和独立成分分析(ICA)常用于特征选择[16]，有些分类器能在训练过程中自动进行特征选择，如决策树(DT)等[17]。目前，智能诊断方法中常用基于统计学习方法的分类器，包括k近邻(k-NN)算法[18]，随机森林(RF)算法[19]，支持向量机(SVM)[20]和人工神经网络(ANN)[21]等。

深度学习方法因具备自动学习能力，也为故障诊断提供一个新的解决方案[22]。深度学习模型即具有多隐含层的深度神经网络，比传统机器学习模型具有更强的非线性特征学习和故障特征分析能力，例如，深度信念网络(DBN)[23]、稀疏自编码器(SAE)[24]、稀疏滤波(Sparse Filtering)[25]、卷积神经网络(CNN)[26]和递归神经网络(RNN)[27]等。

2 基于CNN的风电机组轴承故障诊断算法设计

2.1 基于CNN的故障诊断流程

图1为从样本取得数据预处理、再到模型训练的诊断流程。模型经过训练优化即可用于未知状态样本分类识别，实现对风电机组机械故障分析和诊断。

2.2 数据预处理

原始振动数据是一维信号，无法用于二维图像识别，需对数据转换。图2(a)为简便数据处理方式，将一维信号采样值按顺序重新排成二维矩阵，视作振动灰度图(Vibration Image，VI)。因原始测量数据有限，在构造样本时按一定长度进行重叠采样以增加样本数，如图2(b)所示。

图2 信号预处理Fig.2 Signal preprocessing

本文信号采样和样本构造根据实际采样频率和系统旋转频率等调整单个信号样本的长度(即单个样本所包含的采样点数)。为方便卷积神经网络处理输入图像的边长为偶数，边长为以2为底的指数幂时更利于简化网络结构参数设计，常用样本长度有400=20×20，1 024=32×32，4 096=64×64等。相关文献已证明该信号处理方式有效[28]。

本文还将短时傅里叶变换(STFT)和连续小波变换(CWT)作为信号处理方式。短时傅里叶变换通过时间窗内一段信号来表示某一时刻信号特征。窗长度决定频谱图的时间分辨率和频率分辨率，窗长越长，截取的信号越长，变换后频率分辨率越高，时间分辨率越差。短时傅里叶变换先将一个函数和窗函数相乘，再进行一维傅里叶变换，通过窗函数滑动得到一系列傅里叶变换结果，并将这些结果排成二维时频图。相关公式为式(1)[29]，x(t)代表信号，w(t-τ)代表窗函数，可知短时傅里叶频谱是关于频率ω和时间τ的函数。

X(ω,τ)=〈x(t),w(t-τ)ejωt〉=

(1)

因短时傅里叶变换窗口大小固定，故只适于频率波动小的平稳信号。小波变换可根据频率高低自动调节窗口大小，可进行多分辨率分析。连续小波变换定义如式(3)所示[29]，其中式(2)为小波基函数，s和τ分别为尺度因子和平移因子，分别控制小波变换的中心频率与其在时间轴上沿着信号的平移。s和τ均取连续变化值，是由同一个母函数φ(t) 经过伸缩平移得到一组函数系列，连续小波变换也因此得名。因小波有尺度和平移两个变量，才能将时间信号投影到二维时间-尺度相平面上，利于提取某些时间函数的特征。

(2)

W(s,τ)=〈x(t),φs,τ(t)〉=

(3)

由上可知，与振动信号灰度图相比，短时傅里叶变换和连续小波变换都较复杂，但在解决某些问题时具有优势。本文对上述方法进行实验对比研究，进而在故障诊断效果和分析处理复杂度之间取得权衡。

2.3 模型设计

借鉴于类似LeNet-5卷积神经网络结构，本文初步设计有3个卷积-池化对和2个全连接层的网络结构如图3所示。

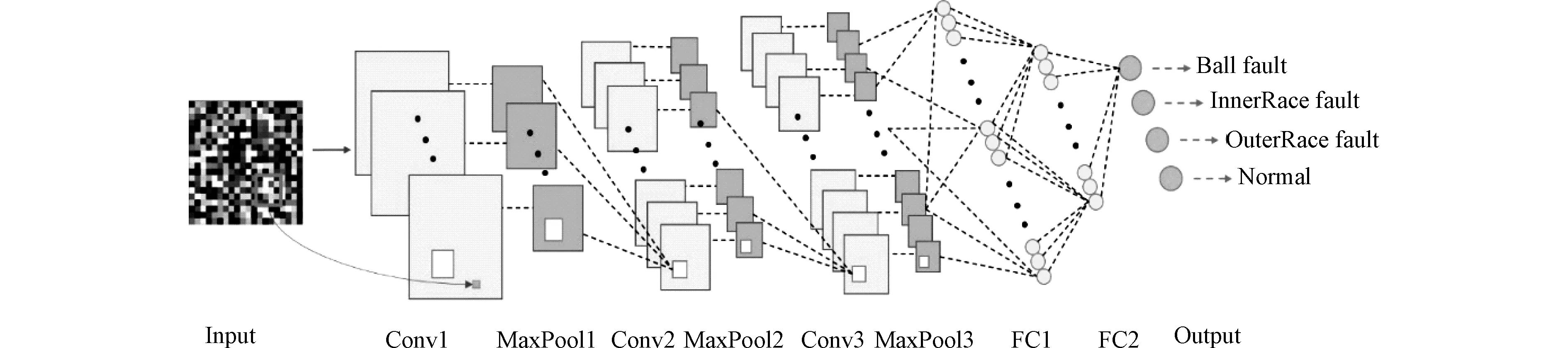
图3 所采用的卷积神经网络结构图Fig.3 Network diagram of CNN

当故障诊断任务变化时，如故障种类增加，可增加输出层神经元个数而特征提取层结构不变，故该网络结构具有一定适用性。本文卷积层采用Same填充方式保持输入输出尺寸不变，池化层采用Valid填充方式即不填充，实现降采样。表1为卷积神经网络模型的结构细节，其中32×32@16意思是有16个通道，每个通道尺寸为32×32，其它各项意思类似。用于训练的细节和技巧还有批量归一化(Batch Normalization)和随机失活(Dropout)，其中批量归一化用在卷积层和全连接层中来加速训练，而随机失活用于全连接层中来防止模型过拟合，提高模型泛化能力，本文随机失活比率采用推荐值0.5[30]。

表1 卷积神经网络网络结构设计

3 实验验证与算例分析

为验证所提方法有效，采用TensorFlow框架[31]进行深度学习编程开发，所有实验均在配置为Intel Core i5 CPU和 GEFORCE GTX 940 M GPU的PC机上进行，选取凯斯西储大学(Case Western Reserve University)滚动轴承试验台的真实数据[32]进行验证分析。

(1)实验平台

图4为滚动轴承试验台，左侧是2马力(hp)电机，提供动力源，中间是扭矩传动装置，右侧是负载电机，也为测功装置。实验时加速度传感器分别安装在风扇端和驱动端电机外壳上方，部分实验也在基座上安装传感器，每秒采样频率为12 kHz或48 kHz。故障轴承安装在驱动端或风扇端分别进行测试，故障缺陷由电火花加工(Electro-discharge Machining)法制造，根据故障位置分为内圈、外圈和滚动体故障。本实验选取采样频率为12 kHz测得的驱动端故障轴承数据与正常轴承数据进行分析。所用SKF轴承设置三种故障直径，分别为0.007 inch、0.014 inch和0.021 inch，代表不同的故障程度。上述各种故障类型和故障尺寸的轴承分别在4种负载大小(0，1，2，3 hp)下进行测试和数据收集。

实验用驱动端轴承参数如表2所示，故障频率为轴承转速频率的倍数，按上文故障频率公式计算。每次实验都用同一型号轴承，而故障点位置和大小不同，一次只设一种故障类型。

图4 美国凯斯西储大学滚动轴承测试台和测试实验范围Fig.4 Public bearing test bench and test range from Case Western Reserve University

表2 轴承参数

(2)实验数据准备

本实验选取三种故障位置、三种故障尺寸和无故障，共10种状态的振动信号来分析，相同故障位置和故障尺寸在不同负载下所测得数据为同一类别。图5为负载为0 hp时10种状态下时域波形图，其中N代表正常状态，BF、OF、IF分别代表滚球故障、外圈故障和内圈故障，07、14、21代表三种故障尺寸。从图5可看出不同故障类型和故障程度的轴承振动信号有明显区别，特别是故障冲击成分的存在，信号总幅值的大小也不同。如正常状态下轴承振动信号幅值较小且平稳，无明显冲击成分，当发生滚动体故障时，存在很明显的冲击成分，不同故障程度下幅值也各不同。从图中还可看出某些故障类型下时域信号具有一定相似性，若无信号处理肉眼较难区分，如0.014 inch和0.021 inch大小的外圈故障。

本实验数据集如表3所示，分别从4种负载状态下原始振动数据中进行重叠采样，不同故障位置和故障程度共计10种状态，每种状态下训练样本和测试样本分别为400个和200个，总计6 000个样本。每种类型在每种负载条件下获取样本数为150个，这是考虑单个样本长度、重叠率及原始振动信号数据总长度之后，获得的比较合适的数据集大小。

图5 测试台轴承故障信号的时域波形Fig.5 Time domain waveform of bearing fault signal from test bench

表3 轴承故障诊断数据集

(3)信号处理方式比较

此处将比较振动灰度图(VI)、短时傅里叶变换(STFT)、连续小波变换(CWT)这三种信号处理方式。

振动灰度图只需对传感器采样到的信号点进行重新排列即可实现。因未进行数据运算，将保留数据的原始特征，可供神经网络进行后续特征提取。图6为不同故障位置和不同故障程度的9种故障类型的振动灰度图，样本信号长度为1 024点，转换后振动灰度图大小为32×32。从图中可看出不同类型振动信号在转换为振动灰度图后纹理表现出不同特征。

图6 测试台轴承故障信号的二维灰度图Fig.6 Two-dimensional VI of bearing fault signal from test bench

本文短时傅里叶变换采用汉明窗口函数，窗口大小设为64，重叠率设为34，则1 024长度的振动信号经过变换后可得33×32的时频图，经简单处理可得32×32的时频图，直接送入卷积神经网络。图7为0负载、0.007 inch故障大小下三种故障类型和正常状态下的时频图，它们之间存在明显区别。时频图横轴代表时间，纵轴代表频率，因信号采样频率为12 kHz，短时傅里叶变换直接得到的时频图覆盖0～6 kHz频率范围，图中省略了坐标值。

图8 连续小波变换得到的时频图和时频图压缩效果Fig.8 Time-frequency map and its compression effect from CWT

图7 短时傅里叶变换得到的时频图Fig.7 Time-frequency map from STFT

本文利用MATLAB 2014a软件进行连续小波变换，并采用cmor1-3小波基函数[33]。图8(a)为部分轴承故障状态下小波时频图，从图可看出小波变换后时频图与短时傅里叶变换后不同，具有更多时间和频率细节。因连续小波变换后时频图在时间轴上分辨率较高，不能直接送入卷积神经网络。本文对原始小波时频图基于三次样条插值进行压缩，压缩成32×32大小。图8(b)为压缩前后滚动体故障下振动信号时频图，可看出仍保留大部分重要图像特征。

本实验对前文设计的10种状态测试。根据一维振动信号处理方式不同，设置三组对照实验。表4为实验结果，从中可看出，三种方式数据处理后的时频图送入卷积神经网络，都可得很高故障识别准确率，接近100%，证明本文的数据处理方法合理和有效。

从表中也可看出：信号处理方式越复杂，模型训练所需时间越短，说明复杂的信号处理已初步提取振动信号故障特征，时频图较好区别，降低了卷积神经网络特征提取难度，故模型很快收敛并有很高准确率。基于振动灰度图的方法，准确率也很高，但训练时间相对较长；此方法不需要专家经验和复杂的信号处理。由上可知，基于卷积神经网络的轴承故障诊断法能在数据质量好的任务中取得较好效果，在无复杂的信号处理和缺少专家经验时能采用振动灰度图的方法实现高效的轴承故障诊断。

表4 基于CNN的诊断结果

4 结 论

本文以风力发电机组齿轮箱轴承的机械故障诊断为背景，分析了基于机器学习的智能故障诊断的流程框架，并提出了具有三对卷积-池化层和两层全连接层的深度卷积神经网络模型设计方法和诊断算法。在此基础上，结合凯斯西储大学(Case Western Reserve University)滚动轴承试验台公开数据集对所提出的机械故障诊断方法进行了实验验证。同时，基于对深度学习诊断模型中采用振动灰度图、短时傅里叶变换时频图和连续小波变换时频图三种不同振动信号变换方式对诊断准确率的影响进行了比较。实验结果证明了所提出的机械故障诊断方法的可行性和有效性。未来工作将进一步优化故障诊断模型，提升其故障诊断准确性和对早期故障的辨识能力，并将继续开展基于深度学习智能诊断方法在齿轮箱不同部件(如齿轮等)的机械故障诊断中的应用。