考虑损耗约束的百万千瓦级海上风电汇集系统分析与设计

李雨佳， 赵海森

(华北电力大学 电气与电子工程学院，北京 102206)

0 引 言

在绿色低碳的大环境下，新能源发电被提出，风作为一种丰富的清洁能源，其发电技术也被用于广泛的研究，相继有世界各地有许多风电工程投入运营。海上风力资源相较于陆上更为丰富，欧洲是全世界范围内海上风电技术的领先国家，到2020年，欧洲海上风电总装机容量将达到24.6 GW[1]；我国海上风电是未来风电行业的重点发展方向，预计到2020年建成30 GW的海上风电[2]。因此，海上风电场的规模将逐步转化为大规模大容量的海上风电集群。

而大规模大容量的海上风电汇集系统的结构需要花费更多的投资成本，一般比陆上要高出2～3倍[3]，大容量大规模海上风电的汇集系统拓扑结构的经济性的优化显得尤为重要。海上风电汇集系统的拓扑优化时一般可看作图论问题，即求解以海底电缆成本为权重的加权边长最小和的问题，但此种方式下得出的仅仅是电缆排布最优的最短路径，而整个损耗不一定是最小的，没有对最后接入点的不同产生的损耗差异进行分析[4]。针对海上风电场经济性等问题，文献[5]通过全生命周期成本的优选模型，对并网方式的经济性选择提供了可靠达到依据，但结论仅适用于一般参考，没有进行具体拓扑分析。文献[6]分析了江苏如东海上风电并网方式及其对应拓扑的投资、维护、损耗成本，比较了交流输电系统，直流输电系统，交直流混合输电系统的总成本，但没对相应的拓扑进行成本优化。文献[7]采用改进蚁群算法对海上汇集输电线路的拓扑优化，但其未考虑损耗约束。

本文从海上风电场内部电气汇集系统的特征出发，根据海上风电汇集系统的经济性组成因素对各个经济性因素建立数学模型，以全局投资成本最低为目标，同时考虑损耗约束条件对汇集系统设计，并在此基础上优化海底电缆拓扑。本文中对风机排布采用放射型模糊聚类算法RFCM(Radial Fuzzy C-Means)与最小生成树算法相结合。对风机进行模糊聚类分片后将聚类片区得出的风电机群的海底电缆分布路径采用Prim最小生成树算法进行优化找出电缆连接最小路径，得出最经济性的分布拓扑，此组合算法能够解决穷举法维数过多的问题，为海上风电汇集系统优化问题的提供了一种快速简洁的方法。本文在此算法的基础上考虑电缆损耗大小因素的约束，得出经济性优良且电缆线路损耗更小的设计方案。最后算例分析一个规划中的海上风电场，证明该组合优化算法与联合优化的有效性。

1 不同接入点的内部损耗分析

海上风电场风机的排布一般分为放射性、环形、链型或者复合型，不同排布的海底电缆线路的各不相同。不同的电缆汇集拓扑会造成每条支路不同段上的电流不相同，每段电流的大小决定其产生的功率损耗的大小，不同的拓扑组合会导致不同的损耗大小结果。所以需要对海上风电场内部汇集网的每一条支路的电流进行计算，才能得到准确的损耗结果。

相同支路的每段电流的大小计算如图1所示。

图1 相同支路的每段电流大小计算Fig.1 Calculation of current of each segment of same branch

根据图1，对于一条支路到汇集点的总损耗可表示为[8]

P=i2R+(2i)2R+……+(ni)2R

(1)

式中：P为电缆线路的总损耗；R为每一段电缆的电阻值；i为电缆通过电流的有效值。

当考虑一个海上风电场的一个片区内的能量汇集的时，海上风电场的汇集系统的拓扑结构往往不是只有一条支路，而是有多条支路汇集到汇聚点，在这种复杂情况的拓扑之下，每条支路每段电流的大小计算示意图如图2所示。图中，n为海底电缆线路的总段数，kj表示该段海底电缆的总电源电流单位注入量，该段的总单位电流注入量视不同拓扑的不同情况而定。

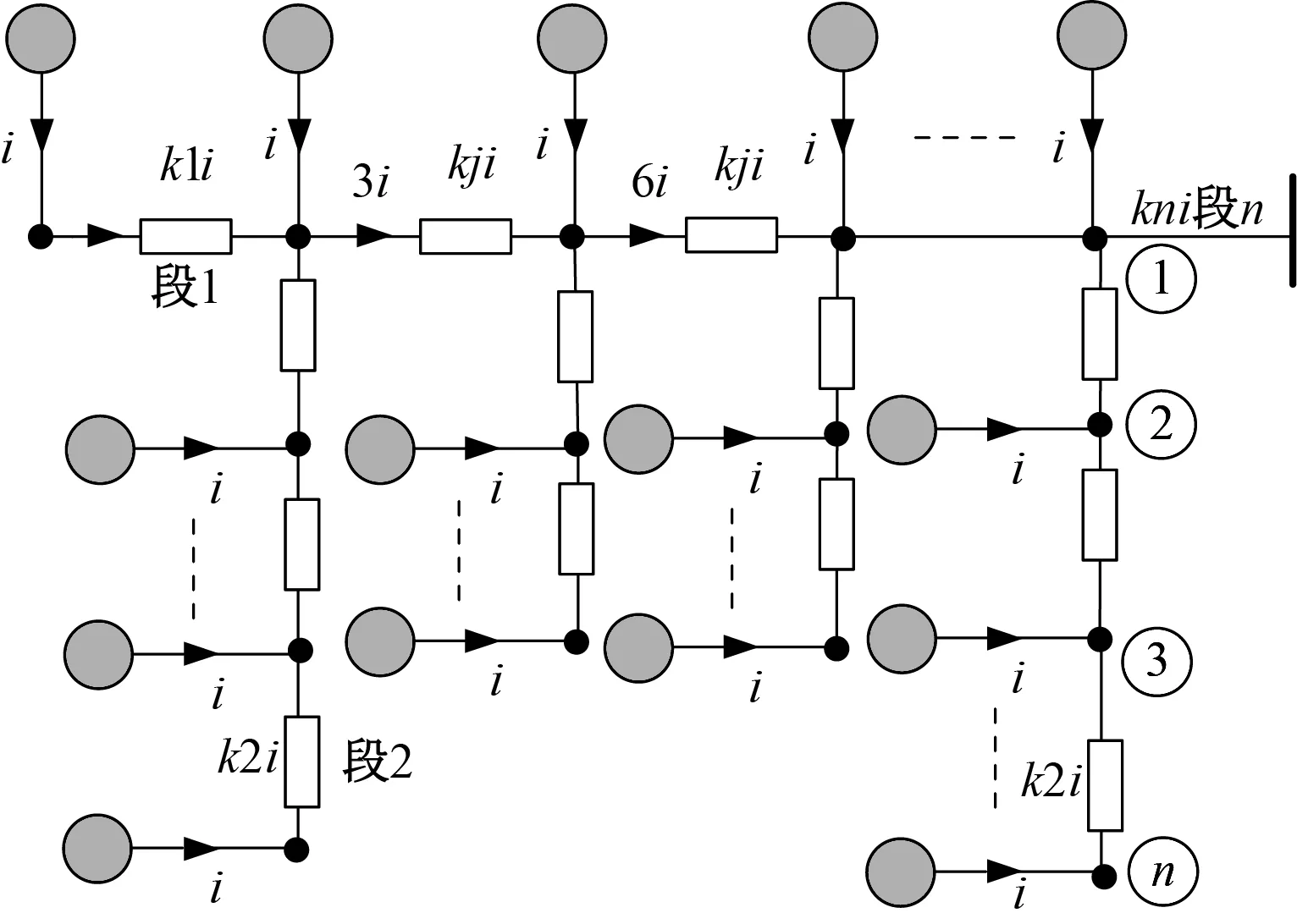
图2 复杂拓扑下的电流大小计算图Fig.2 Calculation diagram of current size under complex topology

根据图2可得到复杂情况下的总电流大小计算式为

(2)

式中：I为每段电流加权和。

故复杂拓扑下的海底电缆线路损耗表达式为

(3)

式中：R为每段海底电缆线路的等效电阻，其阻值大小由该段电缆线路的长度决定：

(4)

将式(4)带入式(3)可得

(5)

不同拓扑会造成不同的损耗，如图2所示，最终汇入点1到n的不同选择会导致整个拓扑损耗完全不一样。

(6)

(7)

(8)

2 计及损耗约束的汇集系统经济性优化建模

2.1 基于RFCM-Prim的经济性优化算法

海上风电集电系统中，风机、机组箱变、开关等优化空间比较小，因为这些与地理位置、附近环境以及资源等紧密相关[9]。海上风电场上每台风机的海底电缆线路的连接方式可以有很多种，连接方式非常灵活，不同的连接方式会导致不同连接拓扑，每种拓扑下的海底电缆线路的长度与型号都不相同。总的来说海上风电汇集系统的经济性各项因素相互关联相互制约，优化经济性的可实现的组合空间很多[10-12]。本节根据海上风电场的特点和约束条件，设计了一种算法，可以较好地解决经济性优化的问题。

算法的主要流程如下：

(1)选择一个大型分区的海上风电场的典型海上风电场，采用放射性模糊聚类RFCM算法对该典型风电场进行变电区域内的风机分区，考虑的条件包海上换流站的位置，换流站容量以及风机之间的距离等。

(2)对每个分区分串后的风机找寻最优电缆拓扑链接路径，这一步可以用图论法和最小生成树Prim算法完成，假设风机为一个点，各电缆连接就是点点之间的线段相连的方法，即图生成树。此步考虑的条件包括风机间的距离，电缆额定容量等。

(3)根据所分片区和风机串的种类计算所有分法下的最优汇集拓扑总成本，寻求最优成本，算法结束。

对于第一步，采用改进后的放射形模糊聚类算法RFCM(Radial Fuzzy C-Means)，对单个汇集区域内风机群的分组(片)。

放射形模糊C聚类RFCM算法是在传统模糊C聚类算法上基于海底电缆拓扑规划的特点进行改进的一种算法。如用传统的聚类算法对一个区域风电场内的风机进行分片，每个片区都存在一个聚类中心点，即海上换流站。但是每台风机均要与海上换流站有连接的通路，且不经过其他的片区，所以一个风电场只布置一个换流站的情况下，采用传统的聚类分类方式会形成如图3所示的风机群块状聚类，造成电缆连接路径复杂交叉。理想的分片方式是以风机接入点换流站为中心，呈放射性分布如图4所示。

图3 块状聚类Fig.3 Block clustering

图4 放射状聚类Fig.4 Radial clustering

所以为了得到放射状聚类分布，对传统的FCM算法进行改进得到新的模糊聚类算法放射型模糊聚类算法RFCM(Radial Fuzzy C-Means)。

用RFCM方式对风机进行分串的步骤为

步骤1：定义各参数数值，包括聚类簇数C，模糊系数m，迭代次数限制N，误差范围ε；读入每台风机坐标f(x,y)和海上换流站的位置坐标O(x,y)，用小于1的随机正数初始化隶属度矩阵U，满足归一化条件如式(9)。

(9)

步骤2：计算风电机群聚类的c个群心(聚类中心)ci，i=1,…,c。

(10)

步骤3：计算目标函数。如果它小于设定的临界值值，或它相对上次目标函数值的改变量小于设定临界值，则算法停止。

(11)

步骤4：计算新的隶属度U矩阵。返回步骤2。更新模糊分类矩阵时，考虑的不再是风机和聚类中心的距离而是与各聚类群心c到海上换流站连线的距离dij，如图5所示，每类聚类群心到海上换流站的连线距离为A，每台风机到海上换流站的距离为B，根据A与B的夹角α的大小计算风机到聚类中心ci与海上换流站的线段的距离dij考虑到方向的问题，定义dij为：当α< 90°时，dij=|B| sinα；当α≥ 90°时，dij=∞。这样可以使位于每类聚类群心到海上换流站的连线距离A前端的附进风机群尽量的聚类在一起，形成图4的放射状聚类效果。

图5 放射型模糊聚类算法RFCM 求dij解示意图Fig.5 Schematic diagram of radiating fuzzy clustering algorithm RFCM to obtain dij solution

所以迭代公式如式(12)所示：

(12)

在此改进下目标函数更新为

(13)

每次迭代判断群心O有没有发生变化用一个矩阵范数比较c(k)与c(k+ 1)，若‖c(k+ 1) -c(k)‖ ≤ε则停止迭代，输出结果，否则进行下一次迭代[13]。

风机群分片之后就可进行拓扑寻优汇集接入的设计。图的最小生成树是指一颗连接图中所有顶点，具有权重最小的树，树的权重为所有树边的权重之和。最小生成树可以应用在电路规划中，规划出既能连接各个节点又能使材料最为节省的布局。计算最小生成树有两个经典算法，分别是Kruscal算法和Prim算法[14]。本文将会介绍Prim算法的原理以及实现。Prim算法是以贪心算法为基本原理，其思路是从某一顶点出发，判断与其相邻的点所连的边的距离，在生成树中加入距离最短即权重最小的边。同理，从当前生成数中的所有种子的顶点出发，选择最小权重相邻边加入其中，以此类推，从而得到最小生成树。

图6 Prim算法求解最小生成树图示Fig.6 Prim algorithm to solve the minimum spanning tree diagram

对于海上风电场风机间的电缆通路，可用Prim算法寻求最优拓扑来使经济性达到最优。具体实现方法如下图6所示，最后得出的绿色路径即为最优经济的电缆拓扑。

2.2 优化模型

一般来说，海上风电场的集电系统包括风电机组，机组箱变、断路器、以及海底电缆线路和换流站组成[9]。其中，风机、机组箱变、开关等优化空间比较小，因为这些与地理位置、附近环境以及资源等紧密相关。而风机就类似于负荷，与风机相连的海底电缆线路与风机在风电场的排布正如电网规划中变电站选址定容的问题，不同的方案，不同的拓扑机构，会整个建设的经济性成本产生较大的影响和差异。

海上风电场上每台风机的海底电缆线路的连接方式可以有很多种，连接方式非常灵活，不同的连接方式会导致不同连接拓扑，每种拓扑下的海底电缆线路的长度与型号都不相同。典型情况下，风机可通过链型、星型、环形等方式组成一个小“队”，而小“队”如何组成并且采用何种连接方接入换流站，能使得在同种运行方式下得到更低的建设投资及其运维成本是值得研究的。因此，海底电缆线路连接方式的组合多样性会造成拓扑的多样性，使之具有较大的不确定性产生可被优化的经济性空间。

海上风电场汇集系统的经济性分析需要考虑不同因素的影响，其中投资成本与各个不同的因素有着直接或间接的约束与联系。本文以海上风电场电气接线汇集系统全局总投资最小为目标函数，对所设计集电系统进行经济性优化设计。

建立总投资成本目标函数：

(14)

式中：Ec为海上风电场汇集系统电气连接的投资费用；Sb为每条线路所传输的视在功率；Sm为每条线路能传输的额定最大视在功率。

经济性影响因素包括投资成本、维护成本以及损耗费用[15]。

(1)投资成本

E=E1+E2+E3

(15)

式中：E1=f1N，为风机配套箱变的投资成本，f1为单价由风电场汇集系统的电压等级决定，N为风机数量，E2=Bi+Si为变电站投资成本包括变压器成本Bi以及其他费用Si；E3=C1+C2，C1为海底电缆总成本是单位长度，总段数以及电缆总长度的乘积，C2为海底电缆敷设成本。

(2)维护成本

根据统计规律可得直流输电系统的维护成本占按照总投资成本的0.5%计算[16]。

(3)损耗费用

(a)换流站损耗

换流站损耗通常由换流站损耗率给出。对于换流站损耗率，交流输电系统损耗率为0.8%左右，直流系统的换流站损耗率约为1.75%[16]。

(b)线路损耗

(16)

式中：P为线路输送总功率;Udc为直流电压输送等级;R为单位直流电阻大小取0.036 6 Ω/km;L为线路长度[16]。

通过经济性建模可分析出，海上风电汇集系统的经济性由各成本因素组成，每个个因素直接相互影响制衡[17]，本文从经济性优化更灵活的海底电缆线路排布角度出发，以投资成本最优为目标对海上风电汇集系统进行优化分析。

2.3 电缆线路损耗约束条件

优化模型的约束条件决定了海底电缆拓扑路径经济性优化的要求，在上述约束条件中，损耗约束即不同点汇入海上换流站的总电缆线路的损耗限制约束，在最小生成树寻最优拓扑过程中，排除聚类中心海上换流站的坐标，根据每一片区风机与放射型聚类中心的位置，不同位置与聚类中心相连会构成许多拓扑场景，使计算量大大加大，因此可限制换流站到个风电区域的距离大小，对计算场景适当削减，减少计算量和时间，根据图2与式(3)可知，与换流站的连接点选择在风机片区的边界上，并且接入点应该尽可能满足使得整个汇集拓扑的串数和段数最小，因此应选择汇集系统风机串中部的点。

本文在全局经济最小的目标下，接入点的位置的选择范围是与聚类中心以γ为半径的圆形距离内的放射片区边界上的节点，如图7所示，每个风机节点相隔(α，β)单位。由于每串电缆的段数决定了每段电流的大小，当接入点接在最边缘，此时串的的加权段数最多，导致电流平方最大Imax2，根据汇集点-汇集段电流矩阵与附加电流矩阵，可得此时最大电缆线路损耗Pmax为

(17)

式中：ilmax为主汇集道上的电流的最大平方和；Ri22为此情况下汇集支路的功率损耗。

因此损耗约束采取电流约束如式(18)所示：

(18)

式中：点(x,y)为拓扑最优经济拓扑下的接入点;γ1为研究过程中限定电源边界与海上汇集点的最远距离。

图7 损耗约束范围示意图Fig.7 Schematic diagram of loss constraint range

3 算例分析

3.1 风电场描述

利用本文提出的方法，对一个规划中的海上风电场进行算例分析。海上风电场面积93 km2，离岸距离40～51 km，离岸距离最远适合使用柔性直流汇集输送。该海上风电场共有80台2 MW的风机，具体参数见表1～3。海底电缆敷设成本30(万元/km)。变流器换流站成本为200(万元/MW)。

表 1 海上风电场风机参数

表 2 海上风电场参数

表 3 中压海底电缆参数

3.2 设计过程

按照前文的的优化算法对半岛北海上风电场中的典型风电场其进行设计，具体如下:

(1)进行变电区域内的风机分片

采用上文所述RFCM模糊聚类方法对风电场进行分成放射型区域，本算例对规划的海上风电场的风机群进行分3片放射机群区与分6片来进行对比，在传统的优化基础上再进行考虑损耗条件的分析，对比不同方案的优化结果。如图8、9为利用MATLAB计算后，得出的风机距离片区图，标出海上换流站的位位置以及分片区的范围。图中五角星为海上换流站的位置，每个点代表风机的位置。

图8 RFCM算法区内风机分6片结果Fig.8 Results of 6 pieces of fan in RFCM algorithm region

图8为将海上风电场区域内的风机进行RFCM算法的分六片区的聚类结果，如图所示风电机群以海上换流站为中心，六片区风机呈放射状分布在海上换流站的周围，为之后Prim最小生成树最短路径寻优做准备。

图9 RFCM算法区内风机分3串结果Fig.9 Results of 3 series of fans in RFCM algorithm region

图9为将图8中的海上风电场区域内的风机进行RFCM算法的分三片区的聚类结果，可以看出以海上换流站为中心，三片区风机呈放射状分布在海上换流站的周围。

(2)寻找最优电缆拓扑链接路径

图10 优化结果：分六串时的拓扑结构 Fig.10 Optimization result: topology with six strings

图11 优化结果：分三串时的拓扑结构 Fig.11 Optimization result: topology for three strings

选取分片后的风机，采用Prim最小生成数算法对其进行电缆拓扑最优路径计算，本文分别得出分3串与分6串时的电缆连接拓扑结构，并且列出海底电缆分6串时的每一区最小路径计算的结果。图10、11为分三串与分六串的整体优化结果，图中五角星为海上换流站位置，各个点为风机的排布位置，蓝色虚线为电缆的拓扑路径。

此路径为经济性最优的路径，当计及换流站损耗约束时，得到最优拓扑如图12、13所示。在该算例下，损耗约束条件γ取3.16×104。

图12 损耗约束下分三串最优拓扑Fig.12 Three series optimal topologies with loss constraints

图13 损耗约束下分六串最优拓扑Fig.13 Optimal topology of divided into six series under loss constraint

4 优化结果

从表4的优化结果可知分片数3时的总投资为1.435亿元要小于分片数6的总投资1.508亿元。相较于穷举法，本文所述算法更具有参考依据，并且能缩短计算时间，对解决海上风电场汇集系统优化更具有针对性，且优化过程更具有可操作性。在考虑损耗约束的条件下，得到损耗较小与经济性较好的综合性更优的拓扑，拓扑中每段汇集电缆上的汇聚电流更小，使总损耗得以减小，如表5所示，无论风电场是分三区还是分六区，考虑损耗约束条件下的损耗大小均小于传统模式，并且总投资相差不到2.8%。

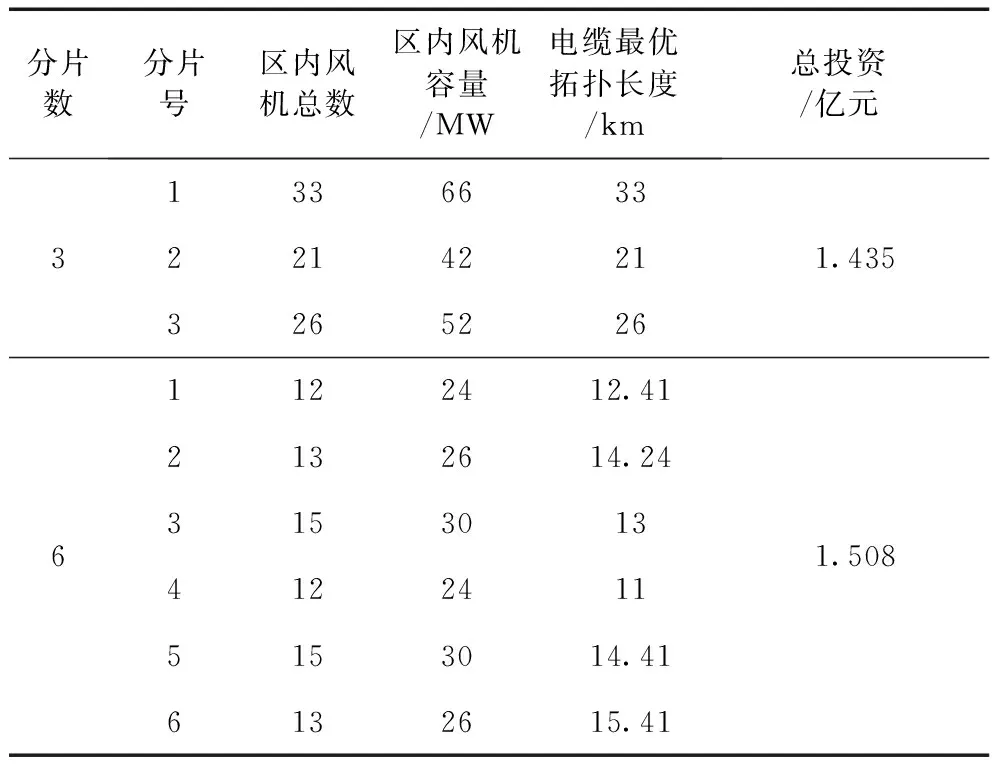
表 4 海上风电场分区优化结果

表 5 海上风电场计及损耗优化结果

5 结 论

本文基于海上风电场内部汇集系统的每根电缆损耗角度分析，建立了计及损耗约束条件下海上风电内部汇集系统全寿命周期成本的优化模型，设计了一种自上而下的组合优化RFCM-prim算法，对大规模的优化问题进行了多次降阶，同时在经济性和损耗大小两者之间选择最优方案。通过一个规划中的海上风电场实例分析，得出以下结论：

(1)分析得出拓扑优化模型，提出一种优化海底电缆拓扑算法采用RFCM算法对该典型风电场进行变电区域内的风机分串，对每个分区分串后的风机用图论最小生成树Prim算法找寻最优电缆拓扑链接路径，对每个分区分串后的风机找寻最优电缆拓扑链接路径。根据所分区域和风机串的种类计算所有分法下的最优汇集拓扑总成本，寻求最优成本，算法结束。

(2)提出考虑电缆线路约束条件下的拓扑设计模型，与单纯考虑拓扑经济性的模型进行比较分析，得出损耗更小且经济性较好的设计方案。

(3)通过实际风电场算例的计算优化对比，论证了设计方法的简洁性与直观性，在考虑损耗约束条件下，每段汇集电缆上的汇聚电流更小，使得损耗大小均小于传统模式，并且总投资相差不到2.8%。为实际的海上风电场规划问题提供了一种科学的定量的规划思路和评估手段，对实际工程实施具有很强的指导意义。