抛物方程(PE)方法在风电场噪声传播中的应用研究

吴鑫波， 朱卫军， 曾明伍， 曹九发

(1.扬州大学 电气与能源动力工程学院，江苏 扬州 225100； 2.东方电气风电有限公司，四川 德阳 618000)

0 引 言

在世界不可再生能源过度消耗的时代，风能作为一种可再生能源受到了全球能源行业的关注，它也是我国大力发展的新能源之一。截至2019年底，我国新增陆上风电装机容量为2 620万kW，海上风电装机容量新增270万kW，总新增装机容量相较于2018年增长达37%[1]。同时，全国风电新增并网装机容量2 574万kW，累计并网装机容量2.1亿kW[2]。然而风力机在带来清洁能源的同时，也带来了一些危害，特别是在沿海发达地区，风资源丰富，分散式风电场备受推广，风力机与人的距离越来越近，其运行时所产生的不间断噪声会影响人的睡眠质量和精神状态，严重危害人的身心健康[3]。因此，关注风电场的噪声传播分布规律，避免居民区处于高噪声区域内，有利于风电的持续发展。

计算声传播主要依靠三大类模型：工程模型、建立在时域上的数值模型和建立在频域上的数值模型。在三种模型中，建立在频域上的数值模型具有比工程模型精度高，比建立在时域上的数值模型速度快的优势。在该模型中，又包括了两种方法：抛物方程(PE)方法以及快速场程序(FFP)。由于PE方法比FFP局限性更小，它不受均匀地表和均匀大气层的限制，因此可以作为风电场噪声传播模拟计算的较优方法。然而国内文献中对PE方法计算噪声的应用研究还主要在海洋声学领域，并未拓宽到空气中的声传播计算[4,5]。同样的，在国外文献中，该方法早期也广泛应用于研究海洋声传播[6-8]，但经过学者的研究发展，在风力机噪声传播方面有了较为成熟的应用。Lee S等用三种方法验证了PE方法的可靠，但只研究了单台风力机在二维的传播，有一定的局限性[9]。Barlas E等应用致动线和大涡模拟方法结合FAST v8/NAFNoise方法与PE方法，深入考虑并综合分析了在尾流、噪声源及地面特性等因素共同影响的情况下，风力机噪声在传播中的声压变化[10]。Cao J等首先用改进Jensen尾流模型模拟了风电场的尾流，然后将模拟结果作为输入，应用PE方法研究了考虑尾流影响的风电场噪声传播，最后用该方法模拟分析了某风电场在不同风向和风速条件下尾流和噪声的变化[11]。

本文选取某兆瓦级风力机组作为研究对象，采用扬州大学基于修正BPM模型自主开发的噪声源计算软件NoiseGen计算该风力机噪声源频谱，利用MATLAB软件基于PE方法，同时应用声传播模型及声叠加理论，编程计算研究风电场噪声，并采用流行商业软件WindPro进行对比验证，对风电场的噪声传播分布规律展开研究。

1 抛物方程(PE)方法

在风电场噪声传播的计算中，PE方法主要用于前期求解风力机噪声在传播过程中的衰减情况，再结合运用声传播模型以及声叠加模型，从而最终求解得到风电场的噪声分布情况。图1给出了本文计算风电场噪声分布的技术路线。

图1 风电场噪声传播计算技术路线Fig.1 Route for calculation of wind farm noise propagation

1.1 噪声源计算

翼型自噪声主要由5种噪声构成[12]：翼型后缘湍流噪声(TBL-TE)、分离/失速噪声(SEP)、层流边界层噪声(LBL-VS)、钝尾缘噪声(TEB-VS)和叶尖噪声(TIP)。

翼型后缘湍流噪声是由于翼型表面流体由层流状态转变为湍流状态，从而在尾缘形成波动的压力场产生的噪声；当风力机在超过临界攻角运行时，翼型表面边界层分离失速，产生了非定常流动，从而出现了分离/失速噪声；风力机在低于106的雷诺数下运行时，层流扩散到尾缘时产生脱落涡，形成了层流边界层噪声；钝尾缘噪声则是由于翼型尾缘过厚，从而在尾缘产生涡脱落形成的噪声；叶尖噪声是从三维角度分析叶片得到的，它是由流体在叶尖周围扰流，从而造成叶尖附近压力的波动而产生的噪声。图2～图5描述了这几种噪声产生的机理。

图2 翼型后缘湍流噪声Fig.2 TBL-TE noise

图3 分离/失速噪声Fig.3 SEP noise

图4 钝尾缘噪声Fig.4 TEB-VS noise

图5 叶尖噪声Fig.5 TIP noise

针对这些噪声，采用扬州大学自主研发的噪声源计算软件NoiseGen计算某兆瓦级风力机的噪声源声功率级。图6中(a)，(b)分别为8 m/s和10 m/s风速时噪声源大小。

图6 某兆瓦级风力机噪声源声功率级 Fig.6 Sound power level of a megawatt wind turbine

可以发现，该型号风力机在风速8 m/s和10 m/s运行时，总声功率级的主导频率分别在500 Hz和630 Hz左右，其它噪声源则处于中低频区域，只有压力面的后缘噪声和叶尖噪声的主导频率处于高频区域内，而相对高频噪声，低频噪声由于其具有传播距离远，危害大的特点，需要重点关注。

在该风力机处于10 m/s的风速下运行时，其噪声源相较于8 m/s风速时的总声功率级略低，究其原因，是该型号风力机在10 m/s风速运行时，超过了额定风速，风力机变桨、偏航运行后，叶片攻角和桨距角的改变导致了叶片表面流动状态的变化，使风力机产生的噪声源降低。

1.2 PE方法

在声音的远距离传播时，可以把声源(风力机)假想为一点，声音从该点处向四周均匀辐射，图7给出了声音传播时的坐标示意图。

图7 声传播直角坐标系和柱坐标系示意图Fig.7 Diagram of sound propagation in cartesian and cylindrical coordinate systems

PE方法的应用即求解三维亥姆霍兹方程：

(1)

式中:keff=ω/ceff(ω为圆频率，ceff为有效声速)；为梯度算子；pc为复杂压力幅值。

在把声源假设为一点的前提下，再忽略其中方位角φ的变化，则可以把上述声音的三维传播简化为在r-z坐标下的二维传播，即可求解简化后的二维亥姆霍兹方程：

(2)

在噪声传播的研究中，一般选取1/3倍频程区间内的频率进行分析，由于更高频噪声的衰减相对较快，在远距离传播中研究价值较低，因此选择频率f=[31.5 40 50 63 80 100 125 160 200 250 315 400 500 630 800 1 000 1 250 1 600 2 000 2 500 3 150] Hz。以式(2)为基础，利用MATLAB软件编程计算，可得到不受翼型等因素影响的声衰减情况。

1.3 传播衰减分析

在噪声传播过程中，地面声阻抗系数影响了噪声的反射率，由于该项目建设于平坦草地，因此可根据式(3)计算其声阻抗系数。

(3)

式中：Z为声阻抗；σ为流阻系数；f代表频率。对于草地类型的地表，据文献[13]其流阻系数取值范围为100 kPa·s·m-2到300 kPa·s·m-2。本文选取流阻系数为250 kPa·s·m-2。

由于计算频率较多，因此本文只选取低(100 Hz)、中(630 Hz)、高(2 500 Hz)频各一种进行分析，并且本文只研究人耳接收到的噪声，因此仅选取距离地面1.5 m高度处的噪声进行分析。PE方法计算所得声衰减如图8和图9所示。其中，图8为100 Hz噪声在r-z平面传播的云图，在图9中，图(a)、图(b)、图(c)分别为100 Hz、630 Hz、2 500 Hz噪声在1.5 m高度处的声衰减。

图8 r-z平面内100 Hz噪声衰减云图Fig.8 Cloud chart of 100 Hz sound attenuation in r-z plane

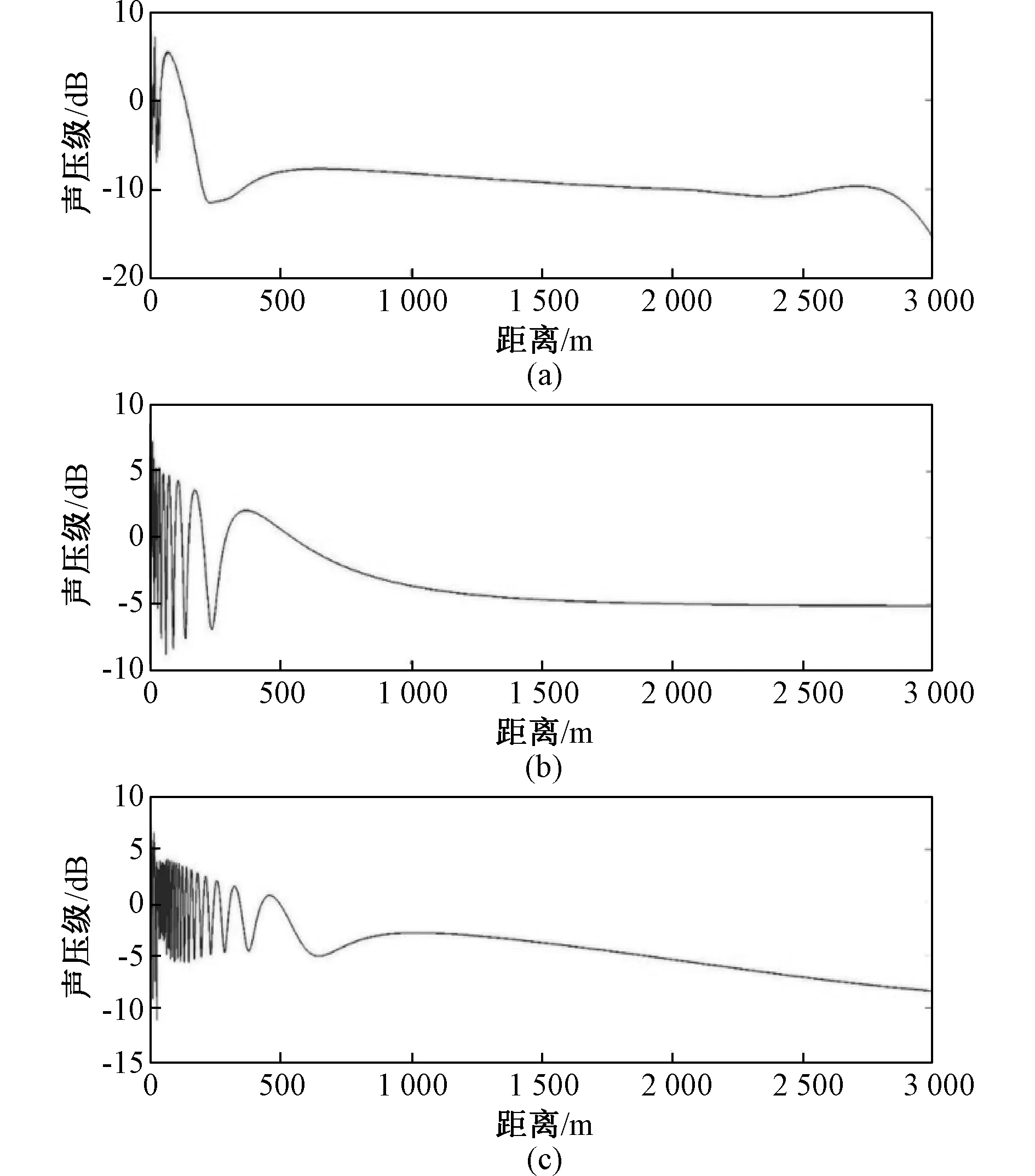
图9 1.5 m高度处声衰减Fig.9 Sound attenuation at height of 1.5 m

从上图中可以分析，声音的衰减并非呈线性，而呈现一种振荡衰减的形式，并且频率越高，其初期的振荡越剧烈，这是高频噪声声波短，相较于低频噪声，其所受地面反射效应更强烈导致的。

1.4 声传播及叠加模型

声传播模型如式(4)所示：

Lp(f)=Lw(f)-10lg(4πD2)-αD+ΔL

(4)

式中：Lp(f)代表频率f对应的声压级；Lw(f)代表频率f对应的声源声功率级，在第一节中已给出；等式右边第二项代表噪声的几何衰减，该项是由噪声随传播距离的增加而发散所产生的；D为声源点到噪声接收点的距离；等式右边第三项代表空气吸收衰减，α为吸收系数；ΔL则为由PE方法求得的衰减，该衰减规律来源于方程(2)，包含了声波传播过程中反射、折射和衍射等物理规律。

声音的叠加需要对数叠加，本文需要应用的声叠加模型模型如下：

(5)

式中：Lp(j)为第j个噪声的声压级；LPTotal为叠加后的噪声。

应用上述模型并利用MATLAB编程，可以计算风电场的噪声传播分布。

2 实例分析

本文选取某兆瓦级大型风电机组进行研究，单台额定功率2 500 kW，风轮直径141 m，轮毂高度90 m。该风电机组布置于平坦地形，并且其周围有5个噪声敏感点，要求该5处区域噪声不高于45 dB，其相对位置示意图如图10所示。

图10 风电机组及噪声敏感点相对位置示意图Fig.10 Relative position of wind turbines and observers

2.1 风电场噪声传播

将各频率、各风力机的噪声先后叠加计算后，可以得到风电场的噪声传播，图11中(a),(b)分别代表风速8 m/s和10 m/s时风电场的噪声云图。

从云图中可以分析，风电场的噪声总体是随着距离的增加而降低的，但是风力机之间会受到叠加效应的影响，使各风力机间的噪声数值偏大。

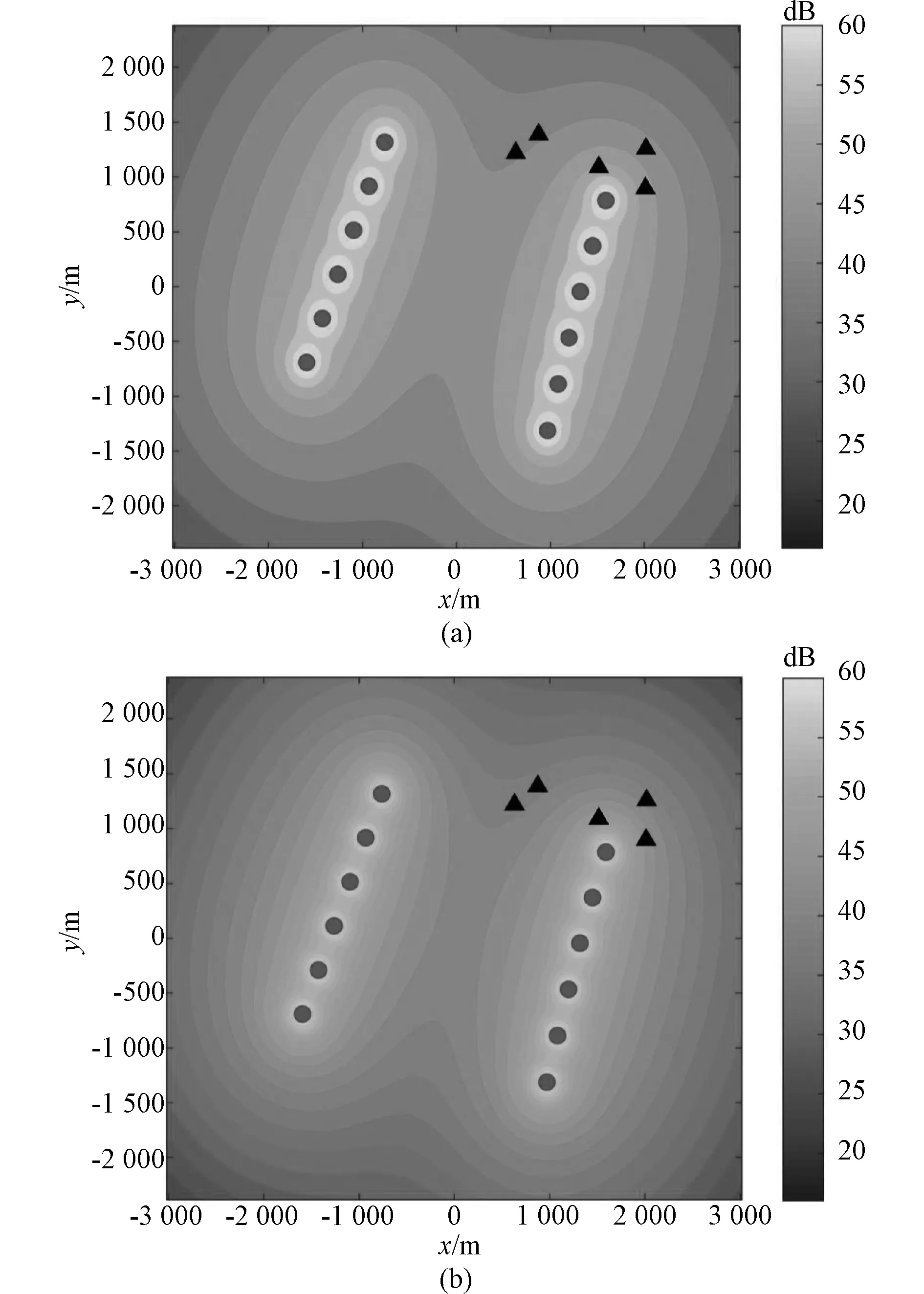
图11 风电场噪声云图Fig.11 Cloud charts of wind farm noise

提取图中各噪声敏感点处的数据，其具体噪声数值大小见表1所示。

表1 各敏感点的噪声情况

从表中数据可以看出，A点噪声声压级总是最大的，其次是E点，这是由于E点相对其他位置更靠近风力机，其他是D,B,C点逐渐减弱。而风速10 m/s时各点声压级比8 m/s时低，这是由于风速达到10 m/s时，超过了风力机的额定风速，此时风力机变桨、偏航运行，造成了声压级的降低。

2.2 WindPro软件与PE方法对比

本文采用商业软件WindPro的计算结果与当前方法进行对比。两种方法之间存在较多区别，表2列出了PE方法和WindPro两者特点以作比较。表3给出了两者计算结果对比情况。

表2 PE方法和WindPro的特点对比

表3 各噪声敏感点在两种风速下WindPro和PE方法的噪声数值对比

对比两种方法的计算结果，可以看出结果大部分都相差±0.5 dBA内，其他结果都在±1dBA左右，相对于WindPro，PE方法计算结果最大差值为3%，最大平均差值控制在1%左右，可以肯定PE方法的准确性与可靠性。

3 结 论

本文针对某兆瓦级风电机组，应用噪声源软件及MATLAB编程，基于PE方法分析了噪声传播衰减的特点，发现中低频噪声在风力机噪声中占主导地位；噪声在传播时通常不是线性衰减，而是以一定的振荡形式衰减；高频噪声的声波短，近距离位置受到的地面反射效应更强烈。同时把PE方法结合声传播模型及声叠加模型，研究了平坦地形风电场的噪声传播，并对比了WindPro软件与PE方法的特点和计算结果，发现PE方法与WindPro计算结果较为吻合，肯定了PE方法计算结果的精度要求和可靠性。

出于对研究的简化，本文并未考虑声指向性对声传播的影响，尽管这种简化在研究风电场噪声传播的普遍规律时有一定的合理性，但精确度还有待更进一步提高。并且本文中仅对平坦地形风电场噪声传播进行了模拟计算，在以后的研究工作中，还需要综合考虑到声指向性的影响以及复杂地形的噪声传播，以期提供更准确的风电场噪声分布情况，从而为风电场布局提供更可靠的支持。