基于长短记忆神经网络的短期光伏发电预测技术研究

李畸勇， 班 斓

(广西大学 电气工程学院，广西 南宁 530000)

0 引 言

随着电力需求的增长，电网规模的不断扩大，传统的大容量集中式发电、远距离高电压传输的互联大电网的弊端日益凸显。随着新一代电力系统的发展，继风力发电之后，光伏电源在电网的渗透率越来越高[1-2]。2016～2019年，中国光伏发电装机容量平均年增长量超过30 GW，是全球市场的主要增长点之一。由于出力的不稳定性，高比例的光伏电源接入电网系统中，会对整个电网的安全运行产生影响。精确的短期光伏发电预测可以帮助电网调度人员合理安排机组启停，制定合理的需求侧响应策略，减小光伏出力波动对配电系统的影响。因此，可靠的光伏发电预测技术对提高电力系统的稳定性、维持电能质量、促进含光伏电网智能化运行极为重要。

光伏发电与日照强度具有强相关性，因此光伏电站是一种典型的间歇式电源。光伏发电预测的精确度强依赖于天气状状态类型[3]，因此光伏发电与天气系统同样具有周期性和季节性。在极端恶劣的天气情况下，光伏发电会由于空气可遮挡因素的增加而存在严重的随机波动，在乌云密布的天气光伏输出功率可能达到零[4]。幸运的是，国内外已有不少机构提供光伏发电预测服务，例如美国的AWS Truepower,法国的MeteoDynSolar，瑞士的Meteonorm等。在国内的国家电网公司D5000系统中，光伏功率预测作为高级应用包含于调度高级应用系统中。这些系统为光伏发电预测的研究提供了大量的历史数据，使得数据驱动的光伏发电预测研究成为可能。

目前，国内外已有不少学者对短期光伏发电预测进行了研究，主要的预测方案有三种：基于概率模型[5，6]，基于机器学习模型[7，8]以及基于多模型组合预测[9-11]。概率算法是一种不确定性的算法，它通过概率论与图论知识的结合，给出下一个时间片的光伏发电在各个值的概率。相较于确定性算法，概率算法拥有更好的灵活性和鲁棒性[12]。但大多概率算法在研究时间序列时，需要基于马尔可夫假设和稳态假设，并非适用于所有的时间序列预测。机器学习模型旨在脱离物理层面直接从数据中挖掘出它们的关联性，在光伏发电预测这种非线性拟合问题上有良好的表现。文献[13]提出了一种基于前馈神经网络的光伏发电预测算法，并使用back propagation(BP)算法提高了预测算法的收敛速度，预测精度在大多数情况下达到了85%以上。文献[14]提出了一种基于多维时间序列局部支持向量回归的光伏发电预测方法，预测精度达到90%。但大多数机器学习方法由于非线性拟合能力过强，对数据噪声敏感度高，在投入运行时无法保证模型的鲁棒性。基于多模型预测方法将非监督学习算法作为监督学习的前驱，从原始数据构建一套完整的光伏发电预测技术方案，是目前数据驱动方法研究中的主流方案。

总的来说，虽然目前光伏发电预测具备大量的技术成果和运行数据，但考虑光伏发电的周期性和季节性方面的研究仍处于初步阶段。长短期记忆神经网络(Long-Short Term Memory, LSTM)是循环神经网络特殊的类型，适用于学习时间序列长短期依赖信息，在语言模型，机器翻译，视频分析等领域得到了广泛的应用[15，16]。对于带有周期性的时间序列，LSTM往往在预测精度上和鲁棒性上表现出更好的预测效果。

本文针对光伏发电的特点，提出了一种基于长短记忆神经网络的光伏短期发电预测模型。首先分析了LSTM模型的学习机制和在光伏预测方面的优势。然后采用相关性分析法得到光伏发电的影响因素，确定了LSMT模型的输入。最后以真实世界的光伏电站数据为例，分别选择两个季节的典型日对提出的预测模型进行验证。

1 光伏发电预测的长短记忆神经网络模型

就像卷积网络是专门用于处理网格化数据的神经网络，循环神经网络(Recurrent Neural Network, RNN)是专门用于处理序列的神经网络。RNN的不同之处在于其网络会对前面的信息进行记忆并应用于当前输出的计算中，即隐藏层之间的节点不再无连接而是有连接的。相较于输入输出固定的传统神经网络结构，RNN可以更好的对时间序列进行建模，但同时，RNN面临着长期依赖问题的挑战[17]。对于一个经典的RNN隐藏单元，有

h(t)=f(h(t-1),x(t);θ)

(1)

式中：h(t)表示隐藏单元在t时刻的状态；h(t-1)表示隐藏单元在上一时刻的状态；x(t)表示当前时刻的输入；θ表示扰动变量。为了更好地说明长期依赖问题，式(1)表示的函数还可以用矩阵乘法表示：

h(t)=(Wt)Th(0)

(2)

式中：Wt代表网络在t时刻的权重；h(0)表示初始时刻的特征向量。当时间间隔不断增大时，除去与初始特征向量的正交部分，权重的剩余分量将被多次相乘，此时梯度消失或者爆炸取决于剩余分量的赋值。

为了存储记忆并对小扰动有鲁棒性，Sepp Hochreiter在1997年设计出了LSTM的结构[18]。LSTM是一种特殊的RNN，其核心贡献在于在每一个计算节点中加入了3个阀门：遗忘阀门、输入阀门和输出阀门。LSTM细胞的结构如图1所示。

图1 LSTM cell结构图Fig.1 Structure of LSTM cell

如图1所示，LSTM细胞中各单元循环连接，代替一般RNN中的隐藏单元，输入单元、输出单元均通过具有非线性的激活函的阀门压缩控制，状态单元线性自循环的权重由遗忘门控制。当阀门打开的时候，前面模型的训练结果就会关联到当前的模型计算，而当阀门关闭的时候之前的计算结果就不再影响当前的计算。因此，通过调节阀门的开关我们就可以实现早期序列对最终结果的影响。LSTM细胞中的状态单元加入了遗忘门控制自循环的权重：

(3)

(4)

因此，单个LSMT细胞内部的状态通过以下方式更新：

(5)

(6)

(7)

除了由LSTM细胞构成的隐藏层，整个LSTM网络还包含输入层和输出层。光伏发电预测的长短记忆神经网络模型将在下一小节特征选择后进行详细说明。

通过在循环神经网络单元上加入阀门，LSTM能够判断模型网络的记忆态(之前网络的状态)在该层输出的结果是否达到阈值，来决定是否将以往信息加入到当前该层的计算中。这种决定哪些信息被遗忘或保留循环的方法是科学而高效的[19]。

2 光伏发电预测的长短记忆神经网络模型特征选择

光伏发电量预测的本质是回归，回归模型的精确度很大程度上取决于算法的输入。光伏发电不仅于光照强度、温度、湿度、云量、降水等环境因素有关，而且与光伏发电站的地理位置、当前的季节有关[20，21]，因此需要从多个维度分析光伏发电预测的影响因素。

短期光伏发电预测准确度与天气状态呈高度相关性，在不同天气情况下，光伏电站的发电量可以相差数百甚至数千千瓦。本文通过基于kendall系数的相关性分析，得到天气状态中温度和云层数量与光伏发电量具有高度相关性。光伏发电量和温度、云层数量的相关性分析图如图2所示。

图2 光伏发电与天气状态相关性分析Fig.2 Correlation analysis between photovoltaic power and weather conditions

图2表明，光伏发电量与温度一定程度上呈正相关性，与云层数量呈明显的负相关性。

与此同时光伏发电具有季节性，不同季节的光伏发电量如图3所示。

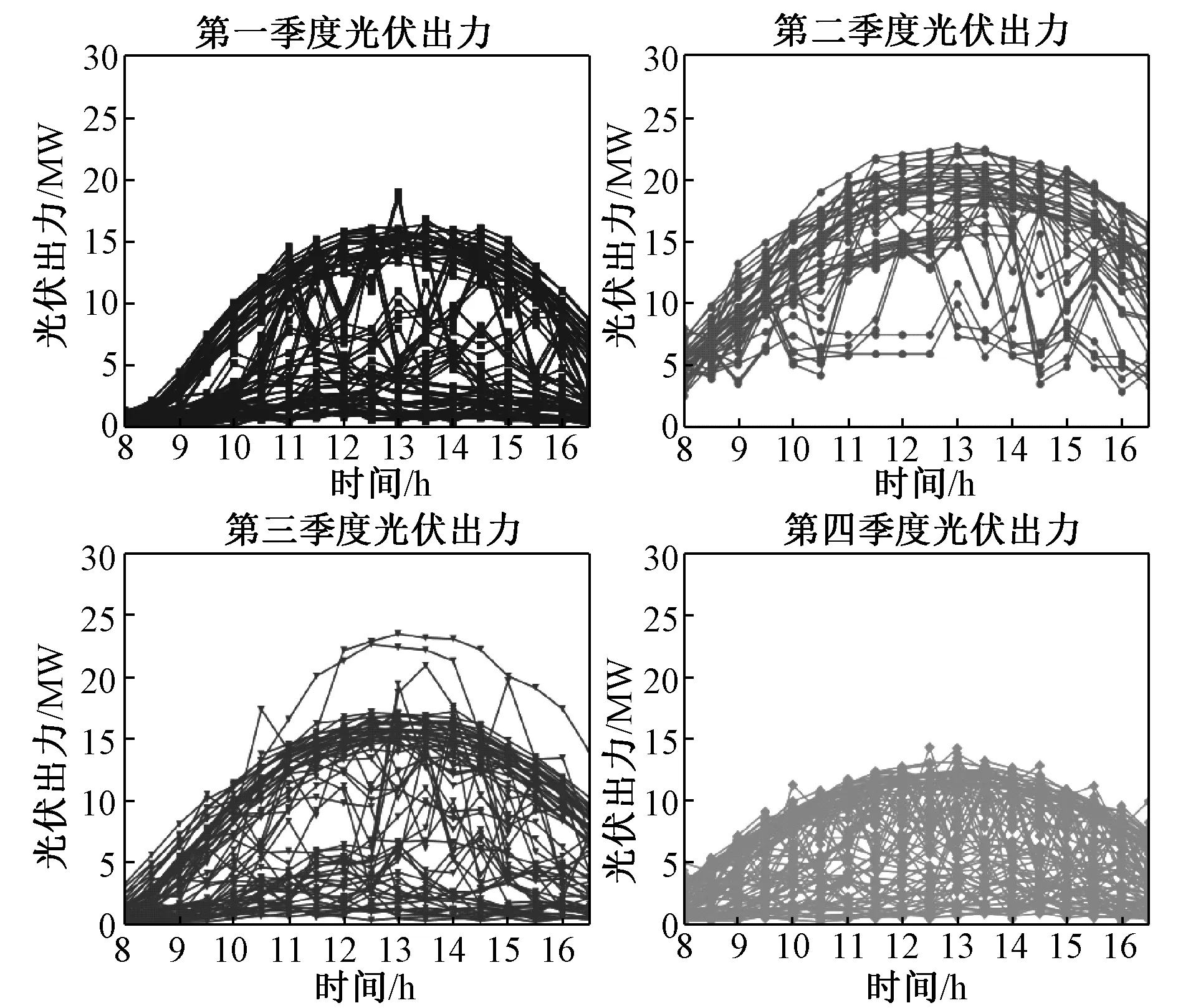
图3 光伏发电季节性波动分析Fig.3 Seasonal fluctuations of photovoltaic power analysis

图3表明，第二季度的光伏发电量明显高于第一、第三季度的光伏发电量，第四季度的光伏发电量明显低于第一、第三季度的光伏发电量，因此，季节也是影响光伏发电的重要因素。

为确保模型的输入尽可能包含所有影响光伏电源出力的重要特征，避免特征过少造成数据挖掘不充分，在现有的特征子集的基础上，加入与温度耦合的湿度、同样含有周期性信息的日类型(周一到周日)作为补充。考虑到选取的特征中，季节、日类型是离散特征，它们不以连续的方式变化。如果直接将这些变量的数字化结果作为模型的输入，不利于光伏出力模型的稳定性。但这种表征时序性特征的变量本身具备连续属性，因此本文采用一次样条插值的方式将离散变量连续化。构建的基于LSTM的光伏发电预测模型如图4所示。

图4 基于LSTM的光伏发电预测模型 Fig.4 LSTM based photovoltaic power forecasting model

图4所示，光伏发电的LSTM模型包含输入层，LSTM层和输出层。构建3层LSTM包含99个输入节点，100个隐藏节点和96个输出节点(日前光伏出力)。原始数据通过输入层输入到神经网络中，经过计算节点时与节点上一时刻的输出进行加权、函数映射处理后进入下一节点，预测的结果即为输入数据不断经过各层计算节点处理后获得的值在输出层函数映射的结果。

3 光伏发电预测的长短记忆神经网络模型训练算法优化

深度学习的优化算法，核心在于梯度下降。神经网络的参数更新有两种方式，第一种，遍历全部数据集算一次损失函数，然后算函数对各个参数的梯度，更新梯度。这种方法每更新一次参数都要把数据集里的所有样本都看一遍，计算量开销大，计算速度慢，不支持在线学习，这种算法称为批梯度下降(Batch Gradient Descent, BGD)。 另一种，每看一个数据就算一下损失函数，然后求梯度更新参数，这种算法称为随机梯度下降(Stochastic Gradient Descent，SGD)。SGD算法的计算量小，迭代速度比较快，但是收敛性能较差，梯度震荡幅度大，能否靠近最优点取决于训练样本的质量。两次参数的更新也有可能互相抵消掉，造成梯度难以下降，进而导致神经网络训练效率不高。

为了克服两种方法的缺点，在训练LSTM模型时，采用一种折中手段：小批的梯度下降(Mini-Batch Gradient Decent, MBGD)，MBGD把数据分为若干个批，按批来更新参数，一个批中的一组数据共同决定了本次梯度的方向，下降起来就不容易跑偏，减少了随机性。另一方面因为批的样本数与整个数据集相比小了很多，计算量也不是很大，每次epoch的时间大大缩短，使得在线学习成为可能，如图5～7所示。

图5 批梯度下降过程Fig.5 Process of batch gradient descent

图6 随机梯度下降过程Fig.6 Process of stochastic gradient descent

图7 小批梯度下降过程Fig.7 Process of mini-batch gradient descent

通过调节模型批尺度在每次循环中分多个批次训练样本，这样既可以利用向量化，有并行运算优势，又可以比批梯度下降法更快的收敛。表1展示了含有100个LSTM节点的神经网络在训练时不同批尺寸的训练效果。

表1 不同批尺寸下LSTM训练效果

表1表明在训练误差相近的情况下，小批梯度下降较批梯度下降节省了将近一半的训练时间，在训练样本数据量较大的情况下，提高了神经网络训练的效率。

4 算例分析

为验证本文提出的光伏发电长短记忆神经网络模型，本小节将提出的模型与现阶段一些前沿的机器学习模型进行对比，并对预测结果进行分析。实验中光伏发电的历史数据来自国网公司智能电网调度控制系统，主要包括每15 min采集一次的光伏发电数据，天气数据来自中国54 511气象台，数据的采集频率为1 h。历史数据的时间跨度为2018年11月1日到2019年10月31日。

数据驱动方法是利用数据训练模型，以构建输入和输出间的映射关系，数据的质量直接决定了模型的预测和泛化能力的好坏。来自不同系统的原始数据采集频率不同，因此首先采用Python Pandas模块对天气数据进行样条插值，补全数据后将两数据按照内连接的方式进行合并。利用drop_duplicates函数剔除运行数据中的重复数据，用pandas.isnull.sum函数检测出变量的缺失比例，在缺失率较低(小于95%)且重要性较低的情况下，使用dropna函数进行数据去空。

为对比模型预测的精确度和效率，在完成数据的预处理后，支持向量回归(SVR)，动态贝叶斯网络(DBN)以及标准循环神经网络(RNN)这三种算法被用来作为对比算法。实验中LSTM的构建与训练使用的是纯Python编写的高层神经网络API Keras。选择Nesterov Adam optimizer作为LSTM的优化器，Adam优化器的优势在于带有动量项的RMSprop，Nadam就是带有Nesterov 动量的Adam RMSprop。

选择电网某一光伏电站在冬季和夏季的两个典型日的光伏发电量作为预测目标，不同算法的预测结果如图8所示。

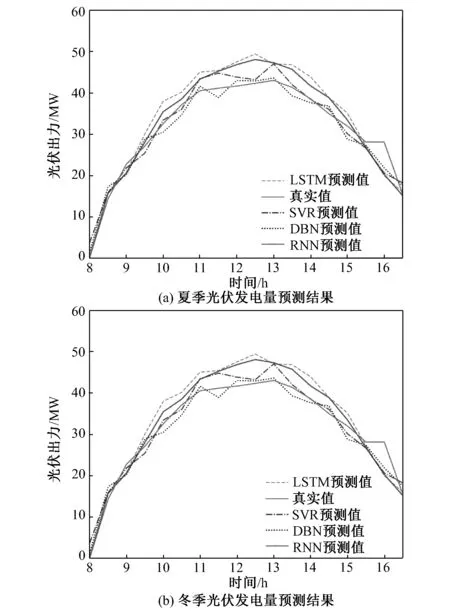
图8 不同算法典型日光伏发电预测结果Fig.8 Photovoltaic power forecasting results of different algorithms at typical days

图8表明，提出的LSTM模型在典型日光伏发电预测较目前主流的机器学习算法更加精确。但在冬季典型日光伏发电预测实验中，几处的预测值偏差依然很大，造成这种误差的情况有两种：一种是由于batch_size选择较大，模型陷入了局部最优，另一种是该时间点处光伏发电波动分量较大，难以通过时间序列模型准确预测。以均方差衡量预测结果的误差，不同算法的预测结果如表2所示。

表2 不同算法的光伏发电预测均方差

实验证明，基于LSTM算法的光伏发电预测，在结合数据清洗、特征工程以及超参数优化的情况下，往往能够得到较为精确的结果。在光伏发电波动分量较小的夏季，LSTM模型平均预测精确可以达到90%。

5 结 论

影响光伏发电的因素复杂多样，且相互耦合。针对现有预测算法在长期依赖关系学习存在不足以及光伏发电与影响因素之间的内在规律挖掘不充分的问题，本文提出了一种基于小批梯度下降LSTM的光伏发电预测模型。实验结果表明小批梯度下降的LSTM较目前主流的机器学习算法有更高的预测精度。提出的LSMT模型可以科学精确的对光伏电站在未来短期内的出力情况进行评估，一定程度上提高了电力系统的经济性、稳定性和安全性，对于电力系统制定调度计划、减轻光伏出力不确定性对电网的影响具有重要意义。