基于核心素养的数学广角“找次品”教学案例探析
何树标


摘 要:“数学广角”单元以培养学生的核心素养为目标,其教学有助于践行课程标准的理念,渗透数学思想方法。统编版小学数学五年级下册第八单元“数学广角”模块为“找次品”,由于在四年级上册学习过“优化”的思想,本单元的学习将进一步深化学生对“优化”这一数学思想的认识,拓展学生的思维,让学生感受数学的魅力,最终掌握分析和解决问题的有效方法。
关键词:小学数学;优化思想;教学案例
一、教材及學情分析
统编版小学数学五年级下册第八单元“数学广角”模块为“找次品”,该内容经常出现在“奥数”题中,小学生学习起来有一定的难度。在小学数学教学中,教师引导学生借助图形、表格或者文字进行分析思考,培养学生的动手能力和思维能力。笔者认为,学生虽然初次接触“找次品”,但根据已有的生活经验,通过动手实践、小组讨论、探究等方式,便不难掌握最优化的解决策略。
本节课的学习目标有两点:第一,让学生能够借助纸笔对“找次品”问题进行分析,归纳出解决这类问题的最优策略,经历由多样到优化的思维过程;第二,让学生感受数学源于生活、广泛应用于生活实际需要,尝试用数学的方法来解决实际生活的简单问题,初步培养学生的应用意识和解决实际问题的能力。教学的重难点是学生归纳最优化的解决策略时可能存在一定的难度,教师要适时引导。
二、教学案例分析
(一)创设生活情境,激发兴趣
与其他学科的特点不同,数学教学具有一定的抽象性,而创设生动有趣的教学情境,能够使教学内容形象化、具体化,同时也能激发学生的好奇心和求知欲,使学生主动参与到教学中。根据小学生的身心发展规律以及个性特点,笔者创设了一个童话故事的教学情境,以此激发学生的兴趣,导入新课。
猪妈妈开了一家糖果店,有一天猪妈妈有事外出,猪小天从货架上取下了一瓶水果糖,偷偷吃掉了2颗。怕被妈妈发现,猪小天又把这瓶糖放回到了货架上。放回的这瓶糖就是“次品”。(PPT课件演示)
师:同学们,你们觉得什么是次品呢?
生:物品的数量、重量、大小等不符合标准的,就是次品。
师:糖果店的货架上有50瓶糖,有什么办法可以找到那瓶次品?
生1:掂一掂,或者倒出来数一数。
生2:还可以用天平称一称。
师:如果一粒一粒地数的话,会破坏包装;单凭用手掂一掂,当两瓶重量差不多时,也不一定能找出来;而用天平,不仅简便,而且准确。此外,要从50瓶糖中找一瓶次品有些困难。在数学上,我们可以从简单的数开始研究,找到规律后再来解决较复杂的问题,这种策略叫做“化难为易”。我们就从3瓶开始研究。
创设新颖有趣的情境,不仅能营造轻松愉快的课堂氛围,渗透“化难为易”的数学思想,还能够唤醒学生的注意力,诱发学生的学习动机,激发学生探究的热情。
(二)理解题意
例题1:现在有3瓶糖果,其中1瓶少了2片,你能设法把它找出来吗?
生:1次就能找到次品。如果天平平衡,那没称的就是次品;如果天平不平衡,那么天平上两端偏上的那一端的就是次品。
师:为什么你断定偏上的那一端就是次品,能说说你的理由吗?
生:因为次品重量轻一些。就像我们玩跷跷板时,体重轻一些的人会在上方,这是一样的道理。
师:能够通过联系生活实际来解决问题,你真棒!
例题2:8瓶糖果里,有1瓶是次品。假如用天平称,至少称几次就保证一定能找出次品?
师:至少称几次能保证找出次品?
生1:如果运气好的话,只需要称一次就能找出次品,第一次称的就是次品。
生2:我觉得不能单凭运气来找次品。如果运气不好的话,一次找不出次品。
生3:每次称两个,不管运气好不好,4次肯定能找出次品了。
师:“至少称几次能保证找出次品”是什么意思呢?
生:既要找出次品,又要做到次数最少。
在数学教学中,正确理解题意至关重要,有助于学生形成良好的审题习惯。笔者引导学生理解本次课的关键词“至少”“能保证”,抓住关键词深挖教材。学生在讨论中明白题意,深入理解题意。笔者总结,“能保证”就要往运气最差的方向想;“至少”是指保证找到次品的各种方法中,称的次数最少的那种方案。此外,笔者编了一个小口诀帮助学生记忆天平的规律:天平平衡,两边一样重;天平不平,下沉那边重。
(三)在“做”中学
美国著名的教育家杜威在《民主主义与教育》一书中提出“在做中学”的教学思想,他认为“所有的学习都是行动的副产品,教师要通过‘做,促使学生思考,从而学得知识”,教师要把“从做中学”贯穿到教学的方方面面。数学新课标指出动手实践、自主探索、合作交流是学生学习数学的重要方式。笔者在授课时积极践行“做数学”的教育思想,在动手操作中锻炼学生解决问题的能力。
师:请同学们继续看例题2,说说你们打算怎样表示找次品的过程?
生1:我想用摆卡片的方式,摆一摆。
生2:我打算用文字加上画图的方式。
生3:我要用手中的学具代替这8瓶糖,然后称一称……
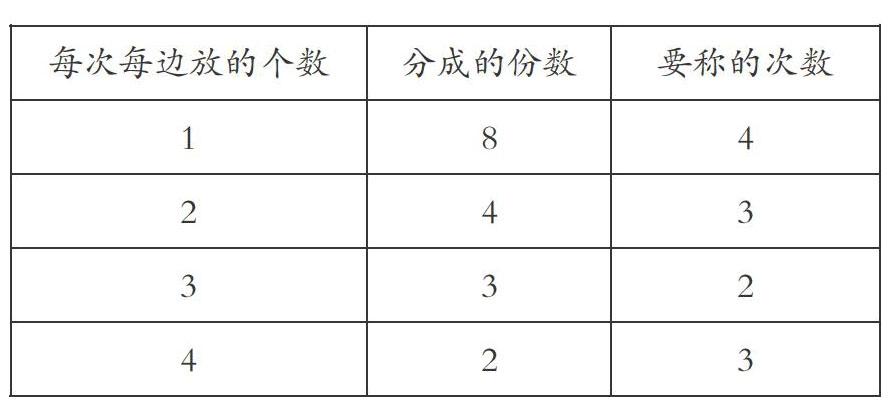
学生各抒己见,经过热烈的讨论后,便采用自己喜欢的方式进行自主探究。笔者在一旁适时提示,比如“若平衡,再放……若不平衡,轻的……”,最后,学生将自己找次品的过程汇总成下表。
笔者引导学生总结出“找”次品的一般规律:利用天平找次品的时候,把待分的物品分成3份,能够平均分的平均分成3份;不能平均分的,也应使多的与少的一份只差1。这样不但能保证找出次品,而且称的次数一定最少。
(四)拓展探究,发散思维
根据维果茨基的“最近发展区”理论,在教学时,教师应着眼于学生的最近发展区,为学生提供有一定难度的内容,调动学生的积极性,发挥其潜能,超越其最近发展区而达到下一发展阶段的水平,然后在此基础上进行下一个发展区的发展。因此,数学教学活动必须基于学生的认知发展水平和已有的知识经验基础。
在例题1的教学中,笔者先以3个糖果为起点,设计的问题相对简单,以此消除了学生的畏难情绪,让学生能较顺利地完成初步的逻辑推理。那就是并不需要把每个物品都放上去称,3个物品中把2个放到天平上,无论平衡还是不平衡,都能准确地判断出哪个是次品。只有理解了这些,后面的探究、推理活动才能顺利进行。在学生基本掌握了找次品的规律后,笔者设计了一道探究性的习题——“在50个金币里面找次品”,以呼应新课导入时创设的教学情境。这样,问题由浅入深、层层递进,使学生在自主探究中收获获得知识的快乐。
例题3:有50枚金币,其中一枚是假币,而外观和真的一样,只是比真币轻一点,你能用一架没有砝码的天平称4次把假币找出来吗?
最优化的解题步骤则为:第一,把50枚金币分成17、17、16三组,先称量17、17两组,若平衡,次品就在16个那组;若不平衡,则在较轻的那17个当中。第二,如果在17枚当中,再将17分成6、6、5三组,如果在16枚当中,再分成5、5、6三组,方法同上进行称量。第三,如果在6枚当中,分成2、2、2三组,如果在5当中,分成2、2、1三组,方法同上。第四,将确定的放在天平上称量即可。这样共需要4次即可找出次品。
最后,笔者引导学生归纳出“找次品”的最优策略:(1)把待测物品分成3份;(2)能够平均分成3份就平均分成3份,如9(3,3,3);不能平均分成3份的,要使3份每份分得尽量平均,如7(2,2,3)。
三、结语
统编版小学数学教材中的“数学广角”蕴含丰富的数学知识,其教学内容结合了学生的日常生活经历,具有极高的研究价值。“找次品”的教学有助于培养学生的优化意识和逻辑推理能力,促进学生思维能力的提高。
参考文献:
[1]王岩,郭微.基于核心素养下小学“数学广角”教学研究[J].数学学习与研究,2019(20).
[2]蒙泽颖.小学高年级“数学广角”单元渗透数学思想方法的教学策略研究[D].贵阳:贵州师范大学,2019.
[3]付瑶.基于核心素养的“数学广角”教学研究[D].哈尔滨:哈尔滨师范大学,2019.

