轮胎刺扎物理过程及其抗刺扎性能改进研究

李冠伦，江 楠，顾寅初，袁晓光*

（1.南通大学 交通与土木工程学院，江苏 南通 226019；2.南通大学 信息科学技术学院，江苏 南通 226019）

当车辆高速行驶时，轮胎有可能因碾压石子、螺丝等尖锐物而造成爆胎，引起重大交通事故。为了增强轮胎的抗刺扎性能，保障行车安全，有必要开发适合现有汽车行驶条件的新型抗刺扎轮胎。尖锐物作用于高速滚动的轮胎类似于子弹冲击防弹衣，因此设想使用芳纶[1-2]抗击尖锐物，并利用芳纶的易加工性[3]衬入普通轮胎。

本工作运用芳纶材料的强抗冲击性并结合传统轮胎材料，系统研究橡胶、芳纶轮胎碾压尖锐物的物理过程，提出一种新型抗刺扎轮胎结构。

1 轮胎碾压尖锐物模型

1.1 橡胶和芳纶的本构关系

首先，由文献[4]得到橡胶、芳纶的应力-应变数据，进行曲线拟合[5]，获得相应的应力-应变拟合曲线，如图1所示。橡胶和芳纶的应力（σ）与应变（ε）的拟合关系式为

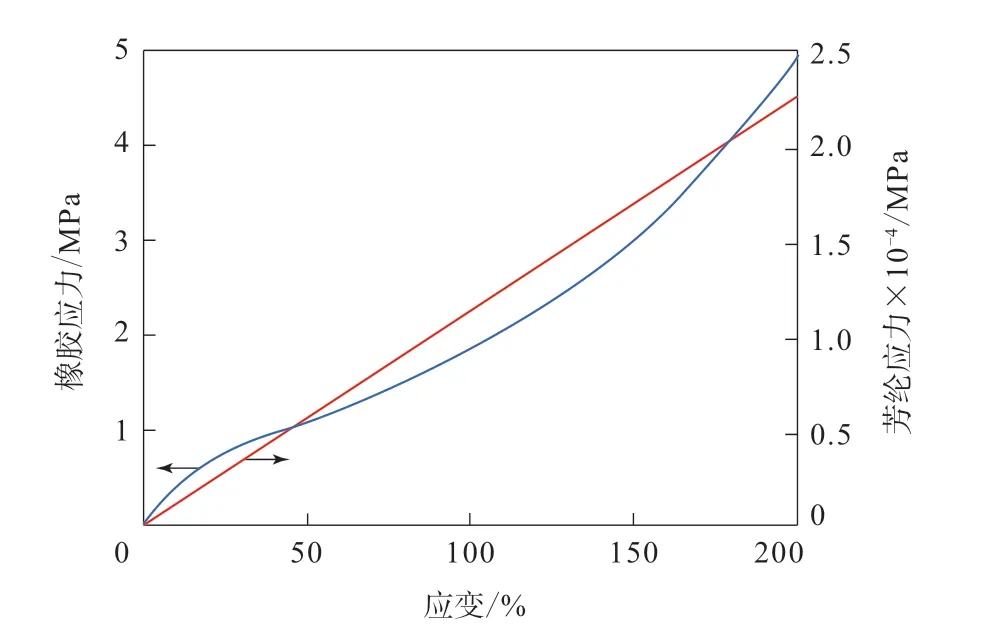
图1 橡胶和芳纶的应力-应变关系曲线

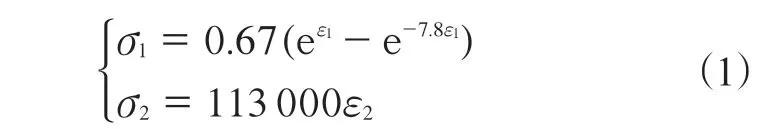
式中，下标1和2分别表示橡胶和芳纶。

从图1可以看出：芳纶的应力与应变大致呈正比关系；两者相比，橡胶的应变范围更大；在相同应变下，芳纶的应力更大，即可承受更大的内力，或在相同内力下，芳纶的变形要小得多。

1.2 尖锐物对轮胎的作用模型

行驶的轮胎经常会碾压尖锐物[6]，见图2，此时轮胎会在接触点发生局部变形。

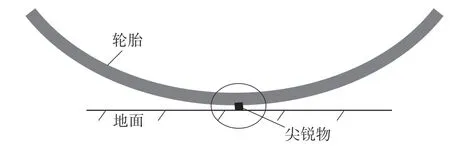
图2 行驶轮胎和地面尖锐物示意

受力分析时认为胎面材料各向同性，取一个自由体如图3所示，即沿着尖锐物轴向以r0为半径[须大于尖锐物的半径（rs）]旋转一周，取部分轮胎。该自由体近似为扁平的圆柱体，在尖锐物的作用下近似变为圆锥体，轮胎截面上作用的主要是拉应力（σ），见图3，r0即为影响半径。

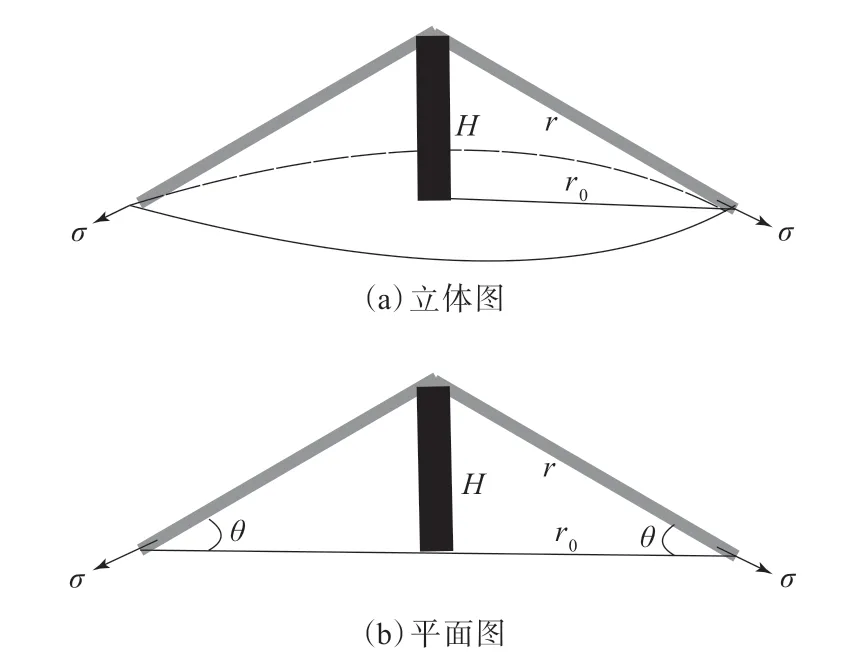
图3 轮胎局部受尖锐物作用下的自由体示意

根据垂直方向的力平衡关系得到

式中，N为尖锐物对轮胎的支撑力，θ为凹起胎面与地面的夹角，A为拉应力的作用面积（圆柱体侧面），则

式中，h为轮胎厚度。

将式（3）带入式（2）得

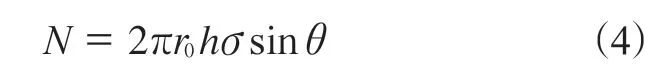
设尖锐物顶起的高度为H（见图3）时，则

同时，在接触点附近原来的半径r0变为r（见图3），由此发生的平均拉应变（fr）为

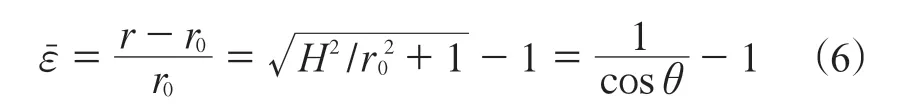
将式（6）代入式（4），并结合式（1），即可建立支撑力与应变的关系式：

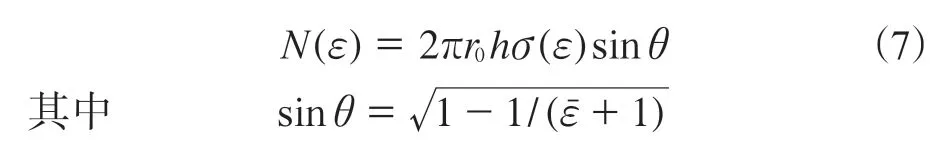
显然，支撑高度越大，应变越大；r0最小可以等于rs，因此rs越小，应变越大，越有可能刺穿轮胎[7-8]。

2 公式的适用性讨论

实际尖锐物与轮胎的接触面积取决于尖锐物的接触面半径，随着轮胎对尖锐物的碾压，接触面积由零变大，刚开始的零意味着一个点接触，但是轮胎此时并未发生变形，亦无破坏；当轮胎与尖锐物开始有接触力的时候，接触由点逐渐扩大到面，接触面半径是影响半径的最小值，影响范围有一个发展的过程，与尖锐物本身的几何特征及支撑力相关。由公式（7）可知，影响半径与支撑力呈线性关系，该关系在接触面外是准确的，即在支撑力一定时，截面（圆柱体外表面）上的拉应力和截取的自由体半径成反比，即

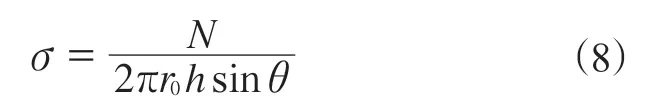
r0的最小值r0min是接触面半径（其值等于rs），可见r0为接触面半径时应力达到最大，即σmax，如图4所示。

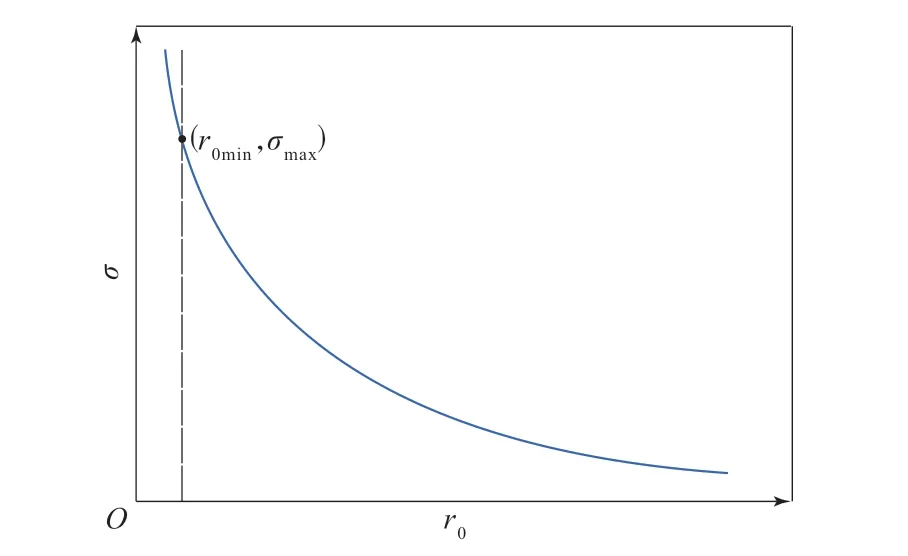
图4 接触点外轮胎拉应力与影响半径的关系

关于在接触面内应力公式的适用性问题，分析如下：从一般的物理事实来看，轮胎总是在接触点及附近破坏，观察应力公式或对应曲线可以发现，当支撑力一定时，尖锐物的接触面半径即r0min越小，应力越大，当接触面半径非常小时，应力会非常大，材料承受不了即发生撕裂，因此应力公式是可以解释这个现象的，也符合圣维南原理对于接触力分布不十分清楚但其合力明确的情况。

3 支撑力的说明及计算方法

以小钢珠与小钢针为例进行比较，来说明支撑力的重要性。小钢针头部和小钢珠具有同样很小的半径。相比钢珠，钢针能轻易刺穿轮胎，就因为支撑力起了关键作用。同时，在一定支撑力作用下，接触面半径须足够小才能产生足够大的拉应力，引起轮胎破坏；反之，如果接触面半径较大，则最大拉应力不足以破坏轮胎，例如轮胎不会被一个鹅卵石刺穿。

从轮胎开始接触尖锐物的点开始，沿中心接触点方向取一个自由体，尖锐物接触面用半径很小的球体来表示，如图5所示。σ′是界面正应力，μσ′是摩擦切应力。

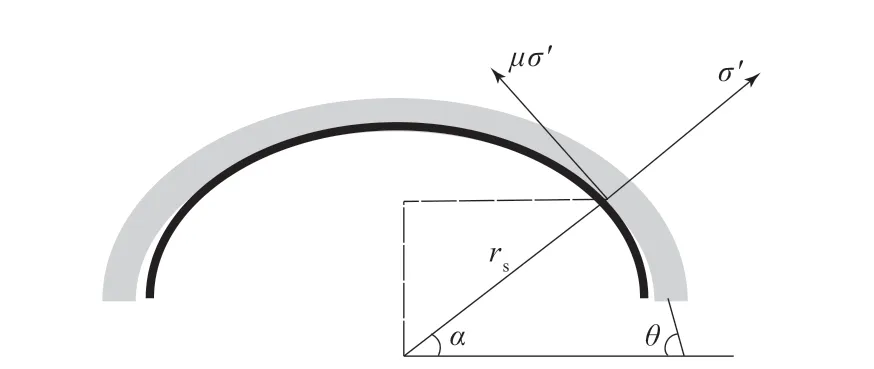
图5 接触面内的正应力和摩擦切应力示意

根据垂直方向的力平衡关系得到

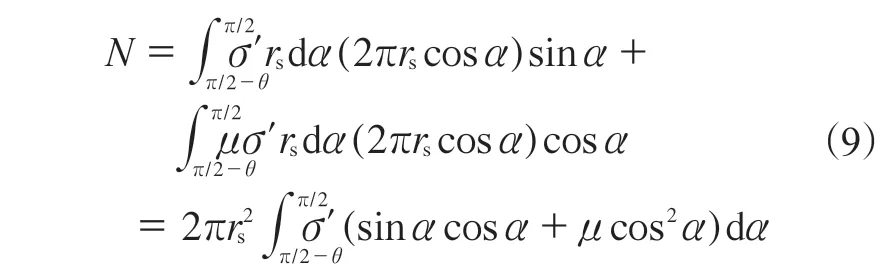
对公式（9）两边求微分得到

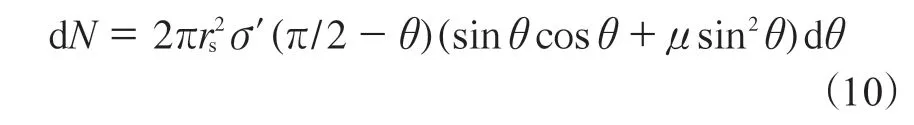
上式表明，轮胎发生刺扎时，θ增大（即影响半径变小），N反而减小，反之则增大。这一现象可由下面的算例来说明。

进一步从最大支撑力和相应尖锐物特征方面探讨支撑力的计算方法[9-10]。最大支撑力（Nmax）应该发生在轮胎刺穿的时候，即在尖锐物的作用下，轮胎材料达到了强度极限，据此改写公式（7）为

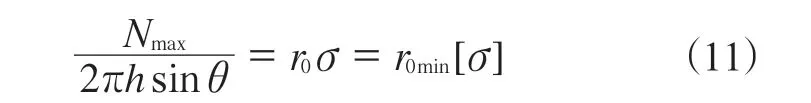
式中，[σ]为轮胎材料的许用拉伸强度。

由此可以看出，一定的尖锐物和轮胎可以确定最大支撑力。除了这3个因素外，需要注意的是变形后胎面与地面的夹角，它是由轮胎变形引起的，公式（6）给出了其与轮胎局部平均拉应变的关系，但是确定该角度需要变形区域上的点应变。考虑轮胎碾压尖锐物的过程，两者开始接触后，影响范围逐渐扩大，直至轮胎开始破坏。变形过程中，r0转变成为r，两者的夹角即为θ。从公式（11）的后两项（即确定的r0min，[σ]）可知，拉应力与影响半径成反比，也就是说，达到强度极限点的拉应力最大，根据本构关系，此时应变也最大，同样道理在影响范围的边缘处，应力和应变最小。因此，在r上每一点的应变不相同，需要逐一求出。影响范围边缘处的拉应力认为是零，接触端的极限应力已知，中间点的应力在这两个值之间，具体计算时可取若干应力值，并根据应力-应变关系算出相应的应变，最后算出相对变形量Δ。

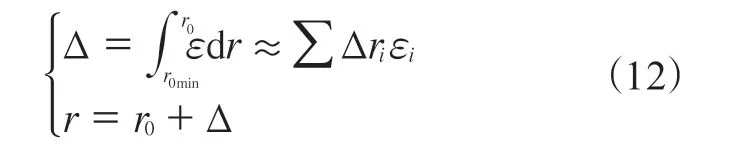
进一步可以确定：

根据公式（11）即可以确定支撑力。

橡胶、芳纶轮胎碾压尖锐物时的计算示例见图6，一根普通螺丝钉的顶头直径为2 mm，橡胶和芳纶的拉伸强度分别为30和1 000 MPa。当螺丝钉全部陷入轮胎时，芳纶的支撑力约是橡胶的10倍，普通汽车单轮对地载荷为5 000 N左右，芳纶轮胎是足够安全的，橡胶轮胎则较危险，不过橡胶轮胎的影响半径要小得多，显示了其缓冲性能优势，因此兼顾二者的优点，提出橡胶/芳纶复合轮胎结构。

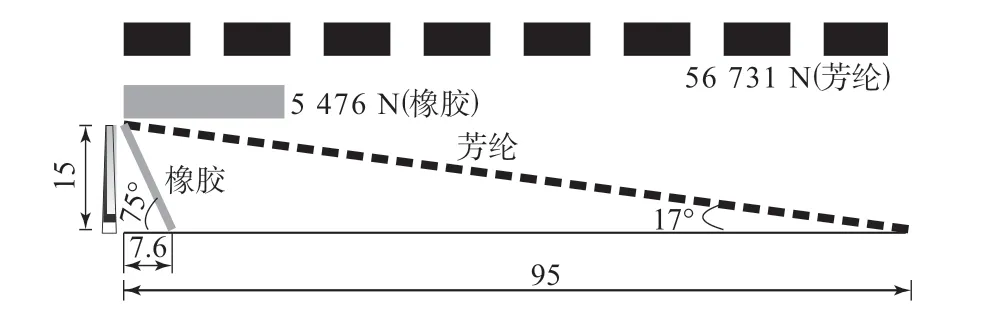
图6 橡胶、芳纶轮胎碾压尖锐物时的计算示例

以橡胶厚度为10 mm，内衬5 mm厚度芳纶为例，计算橡胶/芳纶复合胎面层对尖锐物的作用。根据变形协调，两者具有同样的应变，但应力不同。若芳纶在接触端达到应力极限1 000 MPa，应变为0.088 5，将其带入公式（1）得到对应的橡胶应力，再根据公式（11）分别计算出芳纶层和橡胶层所分担的支撑力（18 910.3和14.5 N）。结合图6可以明显看出，橡胶/芳纶复合轮胎在抗刺扎方面比传统橡胶轮胎具有显著的优势。

前面仅分析了沿r方向的径向应力，其实同一点的环向的应力具有相同的值，这就造成双向受拉的应力状态，对应的莫尔圆是个点，从这个角度看轮胎只能发生撕拉破坏。

4 结论

为了增强轮胎的抗刺扎能力，保证行车安全，本工作研究了尖锐物作用于轮胎的问题并提出了相应的新型轮胎设计思路。

类似于子弹冲击防弹衣，使用芳纶来主要抗击尖锐物，研究橡胶、芳纶轮胎碾压尖锐物的物理过程，依据变形胎面与地面的夹角和支撑力，比较了两种材料轮胎的特点，提出橡胶/芳纶复合新型抗刺扎轮胎结构。计算结果表明，相对传统橡胶轮胎，嵌入芳纶层的新型轮胎能抵抗大得多的尖锐物刺穿力，可以较为可靠地保障汽车的行驶安全。