预应力部分外包组合梁抗裂性能试验

张 鹏， 桂金洋， 邓 宇, 赵晓冬, 孙 飞

(广西科技大学土木建筑工程学院，柳州 545006)

预应力部分外包组合梁是在预应力钢-混凝土组合梁和部分外包组合梁前期研究和应用基础上提出的新型组合结构形式，主要构成方式是采用H形钢或热轧薄壁钢板组合而成具有腹板形式的截面，腹板两侧张拉预应力钢绞线，在翼缘板与腹板之间配置适量的抗剪件并填充混凝土。预应力部分外包组合梁结合了预应力构件和部分外包组合构件的优点，一是钢梁腹部被混凝土包裹，形成良好的约束作用，具有较大承载力和刚度，整体稳定性好；二是施加预应力可以节省钢材，减轻结构自重，降低结构高度,增大承载力，更重要的是由于预应力的存在，提高了构件的开裂和屈服荷载，在相同荷 载作用下减小了变形，非常适用于大跨结构[1-4]。

现阶段，预应力部分外包组合梁在中国工程实践中应用很少，但是随着社会的发展迫切需要这种具有自重轻、跨度大、截面尺寸小和节约材料等特性的新结构形式的出现[5-6]。中外研究工作者对部分外包组合结构已进行了一系列试验研究，形成了比较丰富的理论成果[7-9]，但是这些工作尚未涉及关于预应力引入、抗裂性能和开裂荷载计算等方面的研究。因此，对预应力部分外包组合进行试验分析，重点研究预应力部分外包组合梁的抗裂性能及裂缝规律，为今后预应力部分外包组合结构在工程领域的应用提供计算理论指导。

1 试验概况

1.1 试验目的和内容

试验重点研究预应力部分外包组合梁的抗裂性能及裂缝开展机理，分析预应力水平和截面宽高比对构件开裂荷载、裂缝特征及承载力的影响，基于试验提出开裂弯矩的计算方法。

试验内容包括：预应力对组合梁受力性能及抗裂的影响；组合梁腹部混凝土开裂机理和裂缝的发展；不同截面宽高比和预应力水平的组合梁抗裂性能和承载力；验证组合梁开裂荷载计算方法。

1.2 试件的设计

试验设计2组共8根试验梁，包括6根预应力部分外包组合梁(L1-3P～L1-5P、L2-4P～L2-6P)，2根为非预应力对比梁(L1、L2)。为避免加载过程中剪弯段产生剪切破坏和增强混凝土的包裹效果，所有试件的上下翼缘板之间均焊接直径8 mm的HPB400级横筋，间距200 mm，沿梁全长布置，试验中发挥替代箍筋的作用。考虑到型钢与其所包裹的混凝土接触面易产生黏结滑移，所有型钢腹板中部两侧每间隔300 mm焊接一个φ19 mm(φ为钢筋等级符号)的完全抗剪连接栓钉，栓钉间距根据塑性理论确定，满足完全抗剪连接要求[10]。C30混凝土、试验梁截面尺寸和详细配筋分别如表1、图1所示，钢材性能指标如表2所示。

表1 试验梁设计参数Table 1 Design parameters of test beams

图1 试验梁(L2-4P)截面尺寸及配筋Fig.1 Section reinforcement and dimension of L2-4P

表2 钢材力学性能Table 2 The mechanics properties of steel

1.3 预应力钢绞线张拉锚固

预应力筋采用直径为15.2 mm的1860级钢绞线，试验采用一端张拉一端锚固的张拉方式，锚具一端固定在构件端部的承压钢板后，将张拉端锚具与前卡式千斤顶的端部连接。钢绞线张拉至预定位置后，通过设置在千斤顶端部的局部压缩装置将锚具夹片向内顶进，夹片在顶压作用下挤压套筒，产生握裹力，最后卸载，即完成锚固。因张拉端锚具采用顶压时不允许夹片随钢绞线移动，最大限度地减少锚具回缩量，同时形成更大握裹力，可有效控制加载时荷载增大和锚具变形引起的梁端滑移。

1.4 试验装置和加载方案

试验采用量程1 000 kN的液压千斤顶，荷载通过分配梁传递，三分点加载，装置如图2所示。正式开始前先预加载，消除连接装置间隙，观测仪器数据是否正常。开裂前，每级荷载增量为3 kN，以保证开裂荷载和裂缝的量测，开裂后每级荷载增量为10%的计算极限荷载，当荷载降至极限荷载的85%时卸载。每个加载步匀速进行，且持荷10 min。

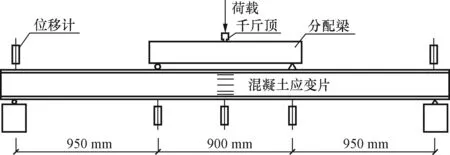
图2 试验装置Fig.2 Test setup

2 试验结果和分析

2.1 试验结果

试件的主要试验数据如表3所示。

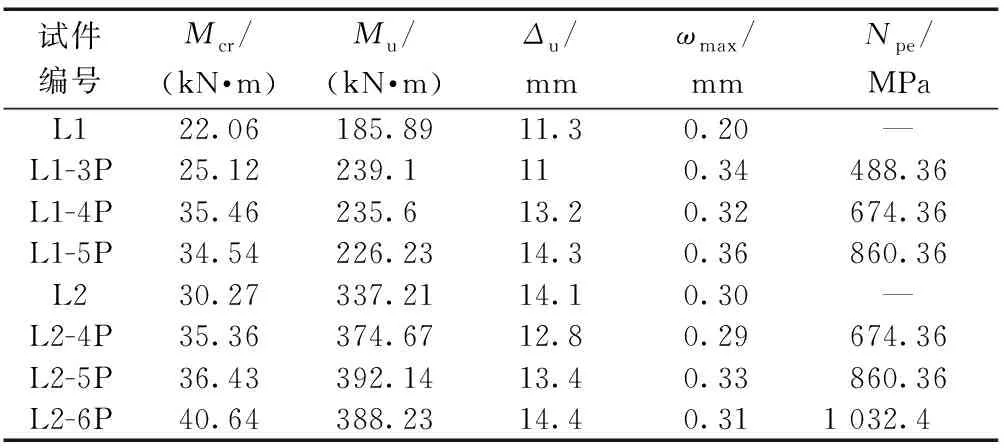
表3 主要试验结果Table 3 Main test results

2.2 荷载-挠度曲线

图3为截面宽高比不同的2组试验梁的荷载-挠度曲线。由图3可以看出，试验梁在施加预应力后，开裂荷载均有不同程度的提高，承载力得到提升；随着预应力水平提高，对宽高比为1.0的组合梁影响更明显，因而极限承载力提升幅度更大；从屈服至破坏阶段，高持荷能力强，相较于非预应力梁，其破坏时的挠度增大，且卸载后有较好回弹量。

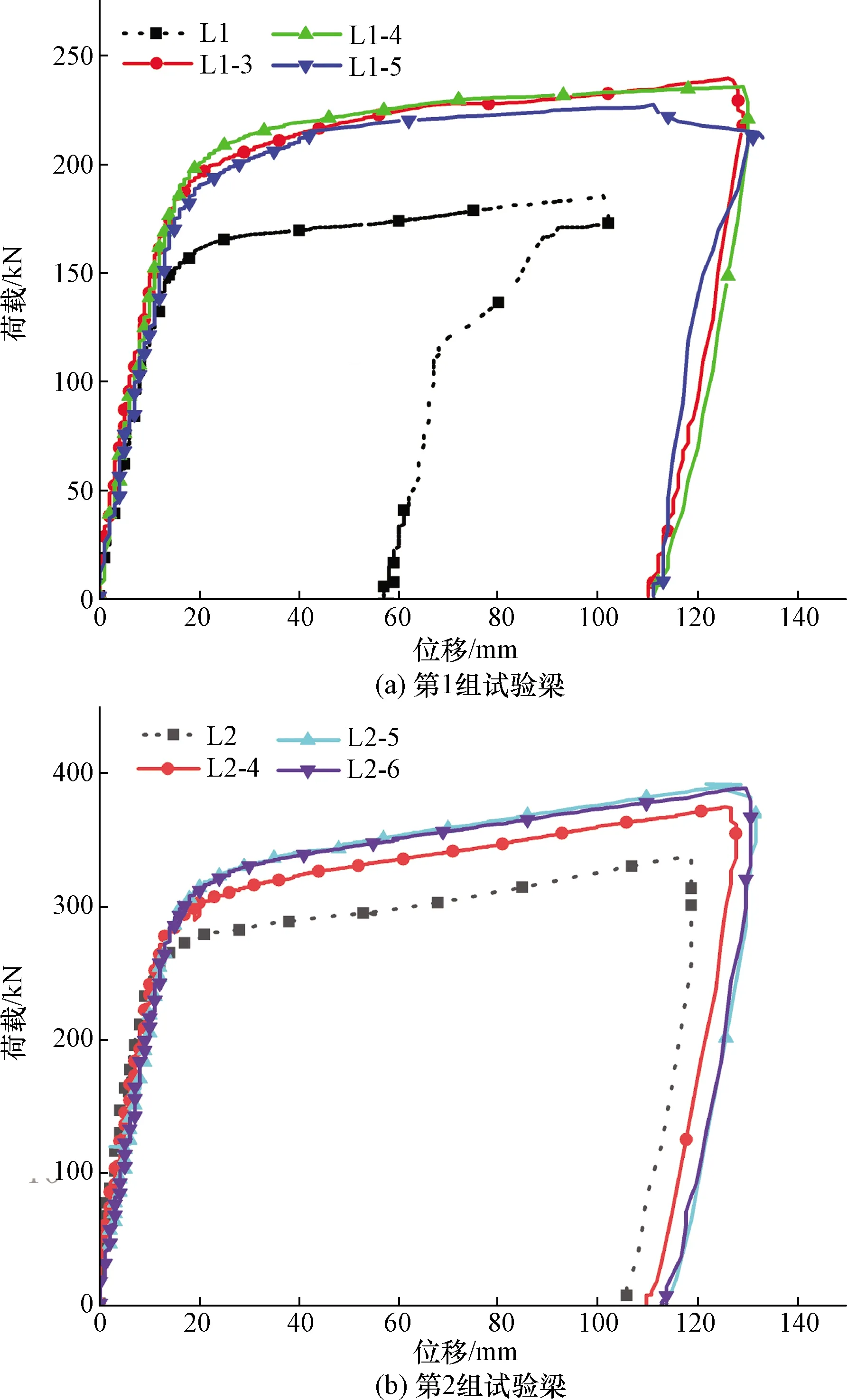
图3 不同截面宽高比试验梁荷载-挠度曲线Fig.3 Load-deflection curve of test beam with different section height-width ratio

2.3 跨中截面型钢和混凝土应变

图4为第1组试验梁混凝土应变分布，Pu为峰值荷载。由图4可以得出，非预应力组合梁先于预应力梁开裂，开裂前符合平截面假定。混凝土开裂后，非预应力组合梁曲线出现折线，不再满足线性关系；预应力组合梁从开裂至0.7Pu，由于钢绞线对弹性阶段的刚度贡献较大，其应力-应变曲线一直为直线或近似直线。说明部分外包组合梁中引入预应力，一方面利用预压力增大了开裂弯矩，延缓裂缝；另一方面增大了截面刚度，使其在开裂后的一定范围内保持较好的弹性工作性能，承担更大荷载。

图4 试验梁混凝土应变Fig.4 Test beam concrete strain

图5为第1组试验梁的型钢腹板的应变分布，由图5可以看出，当腹板受拉区混凝土开裂后，其截面应力-应变曲线仍具有较好的线性关系，基本与混凝土截面应力-应变曲线保持协调。将图4、图5的试件应变图进行一一对照分析后，得出在相同荷载作用条件下，型钢与混凝土截面普遍存在一定的截面应变差，表明型钢与混凝土的连接即使是按照规范采用的完全抗剪连接，仍存在相对滑移现象，难以避免。但是考虑到两者的截面应变差较小和加劲肋构造的增强作用，在进行相关的抗裂和抗弯等理论分析时，可忽略相对滑移，对结果影响很小[7]。

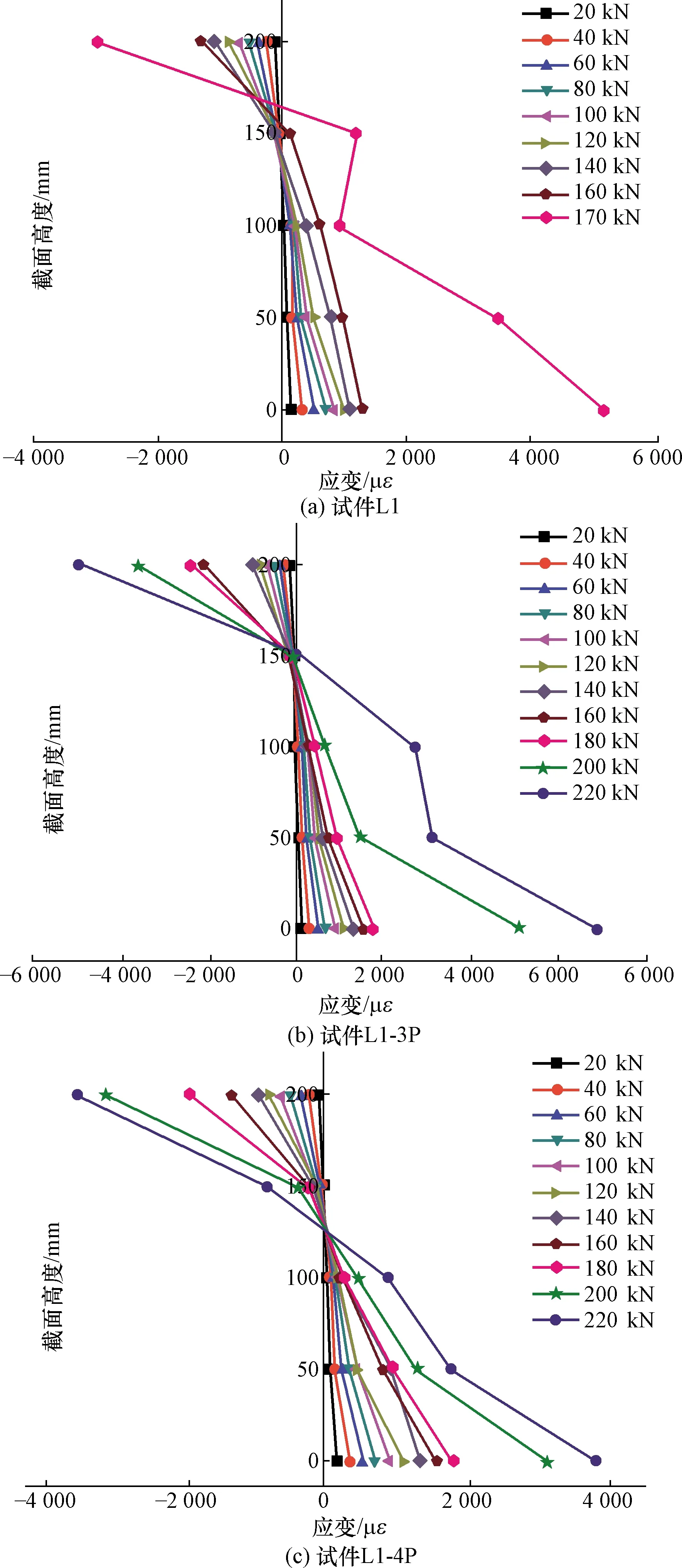
图5 试验梁型钢应变Fig.5 Test beam steel strain

2.4 开裂荷载曲线

图6为试验梁的开裂荷载-预应力水平曲线，可以得出以下结果。

图6 开裂荷载-预应力水平图Fig.6 Cracking load-prestressed horizontal diagram

(1)将非预应力梁L1和L2与预应力梁对比，预应力施加提高了开裂荷载，对第1组宽高比0.77的效果优于宽高比为1.0的试验梁，但预应力水平越高，影响效果减弱。

(2)对于第1组试验梁，一定范围内，开裂荷载与预应力水平成正比，但预应力达到40%左右后开裂荷载略微降低，说明试验梁已经接近最佳预应力水平。

(3)对于第2组试验梁，开裂荷载与预应力水平正相关，始终保持较稳定的增长态势。

综合来看，一定范围内，预应力部分外包组合梁的开裂荷载与预应力水平成正比，且宽高比为0.77的组合梁在较低预应力水平时更易于达到最佳抗裂性能；其他条件相同时，宽高比为1.0的组合梁的抗裂度大于宽高比为0.77的组合梁，但预应力的引入明显减小了宽高比不同所引起的开裂荷载差值。

2.5 裂缝特征及机理分析

图7为2组试验梁主裂缝宽度曲线。由图7可以得出以下结果。

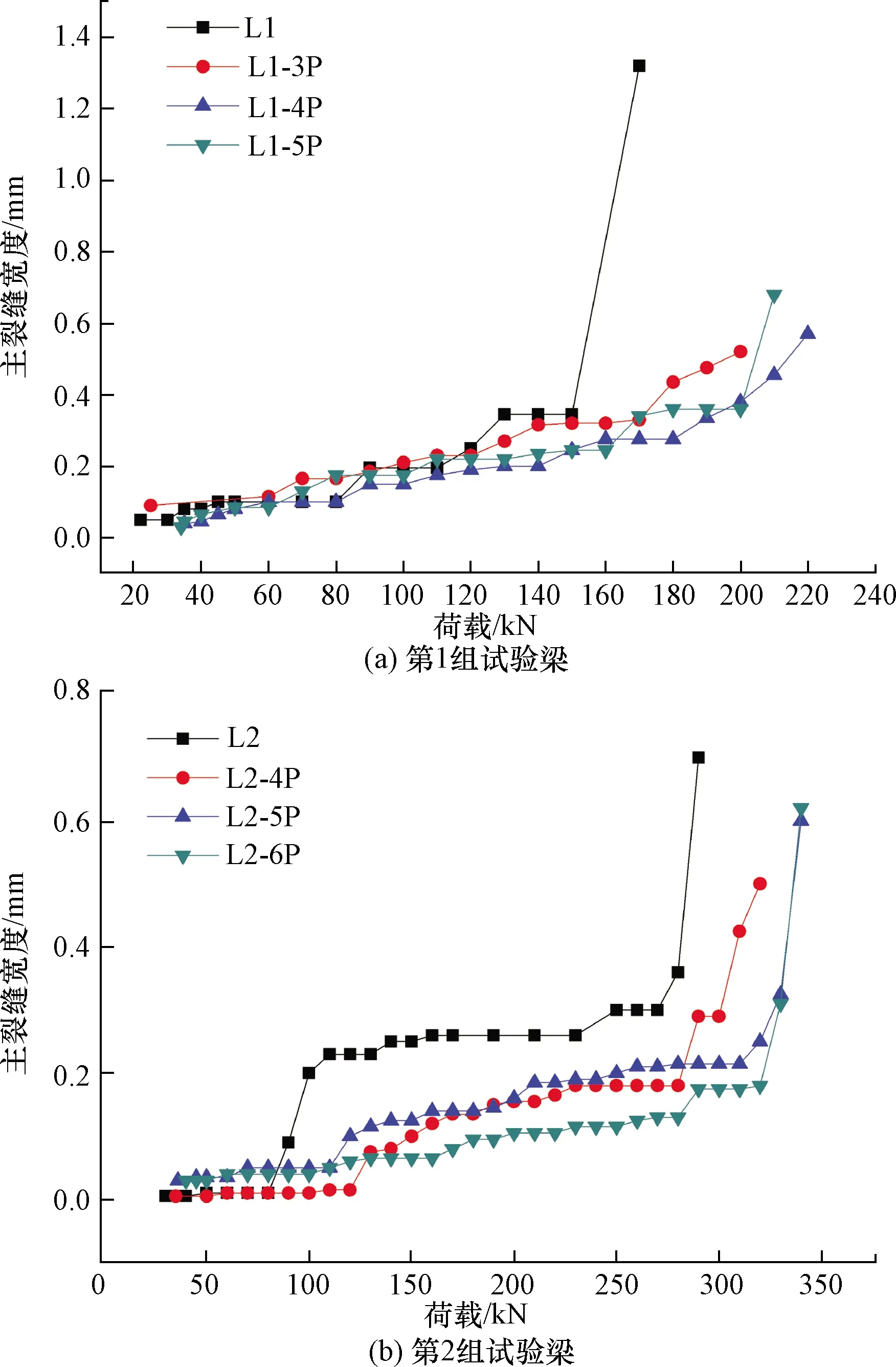
图7 试验梁主裂缝宽度Fig.7 Main crack width of test beam

(1)将L1-3P～5P、L2-4P～6P分别与L1、L2对比，预应力施加后试验梁的主裂缝开展比较缓慢，破坏时的主裂缝宽度显著减小，承载能力得到大幅提升。

(2)将L1-3P～5P及L2-4P～6P分别对比，随着预应力水平的提高,2组试验梁的主裂缝宽度均有比较明显改善，对裂缝发展速度影响较小。

(3)将2组试验梁对比，第2组截面宽高比为1.0的试验梁加载阶段的主裂缝宽度和发展速度明显小于第1组，特别是从开裂至0.35Pu左右时裂缝宽度几乎没有发展；从裂缝出现至急剧增大阶段，宽高比为1.0的预应力梁和非预应力梁的曲线相较于宽高比为0.77的更分散，说明预应力对截面宽高比相对较大的试验梁抗裂性能影响更明显，在工程实践中控制裂缝延伸开展、提高抗裂能力会更加理想。

图8为所有试验梁的整体裂缝形态图，结合试验现象，可以得出以下结果。

图8 裂缝分布Fig.8 Fracture distribution

(1)试验梁的初始裂缝没有出现在纯弯段，均发生在梁中间的加劲肋与型钢下翼缘板连接处。随着加载进行，裂缝缓慢向上发展至1/3梁高后停止延伸，纯弯段裂缝相继出现，其原因有：一是加劲肋处截面几乎全部由型钢组成，截面刚度大，与横筋、腹部混凝土组成的截面刚度差较大，导致加载初期截面的应变差大、变形不协调；二是因为试验采用三分点加载，经分配梁传递的集中力直接作用在左右侧的加劲肋上部，裂缝易在集中荷载作用处产生。

(2)预应力和非预应力组合梁的平均裂缝间距比较接近，但预应力组合梁的主裂缝间衍生裂缝较多且宽度稍大。说明预应力筋增大了截面刚度，改变了组合梁受力性能，在较高荷载水平下，持荷能力好，材料强度得到充分利用。

(3)将L1-3P～5P、L2-4P～6P分别与L1、L2对比，预应力和非预应力组合梁的最终裂缝分布形态差别不大，其中最显著的区别是预应力组合梁纯弯段受压区混凝土裂缝比较集中，沿梁长度方向连通，破坏时压碎区面积较大且特征明显，型钢上翼缘起皮现象更严重。

(4)L1-3P～5P以及L2-4P～6P对比，随着预应力水平提高，裂缝数量变化不大，但在承载力大幅提升情况下其延伸高度显著降低。说明预应力增大，截面的预压力随之增大，不仅提高了开裂荷载，而且使开裂后钢绞线分担更大的弯矩作用，其抗拉强度高、抵抗变形能力强的特点得以有效发挥，从而抑制了钢绞线上部的裂缝延伸，体现预应力大小对预应力部分外包组合梁阻裂性能的重要作用。

3 开裂荷载的计算

预应力部分外包组合梁在外荷载的作用下，钢梁腹部受拉边缘混凝土拉应力与预压应力相互抵消，此时组合梁处于消压状态。在混凝土拉应力增大至开裂期间，预应力部分外包组合梁的受力与非预应力组合梁相似。因此，预应力部分外包组合梁的开裂荷载可认为由相同条件下的非预应力组合梁开裂弯矩和消压弯矩两者叠加得到。其中预应力部分外包组合梁混凝土在受拉区应力达到混凝土 抗拉强度标准值ftk时，混凝土应变为εtk，此时组合梁处于弹性阶段，沿截面高度方向变形协调，开裂时其截面应力和应变分布如图9所示。

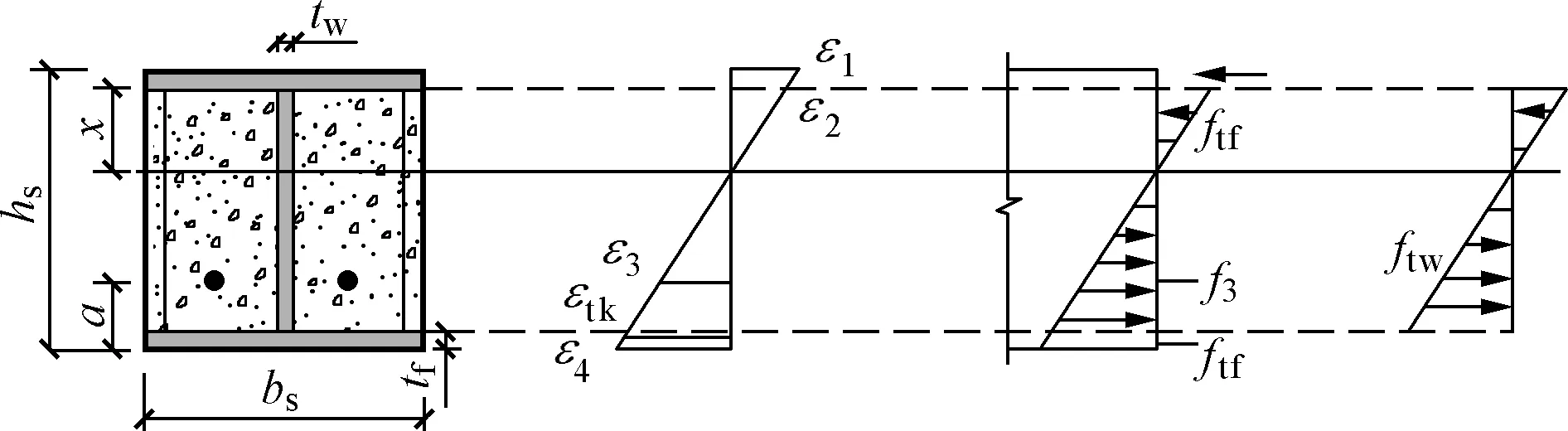
x、hs和tw依次为截面受压区高度、腹板高度和厚度；bs、tf为翼缘宽度和厚度；ε1和ε2、ε3、εtk及ε4分别为型钢上翼缘的上下表面、钢绞线重心、型钢下翼缘的上下表面位置处的应变；和ftf、ftw及f3分别为型钢上下翼缘合力点、腹板和钢绞线重心处的应力图9 截面应力和应变分布Fig.9 Cross section stress and strain distribution

利用换算截面法，将腹板和翼缘分别换算为混凝土面积，则部分外包组合梁换算截面面积A0为

(1)

式(1)中：Ec、Ey分别为混凝土和型钢弹性模量。

根据面积矩相等得到受压区高度x：

(2)

由式(2)受压区高度x计算截面惯性矩I0：

(3)

W0=I0/(hs-x)

对照组患者并发症检出率是25.81%,与研究组的3.23%相比高出许多,统计学存在差异(P<0.05),详情如下表2:

(4)

σpe=Npe/A0+Npeep/W0

(5)

式(5)中：W0为受拉边缘截面抵抗矩；σpe为预应力钢绞线的有效预拉力；ep为偏心距；Npe为有效预应力。

消压阶段弯矩Mcr1为

Mcr1=σpeW0

(6)

由图9得到型钢上翼缘上下表面应变ε1、ε2和钢绞线重心应变ε3：

(7)

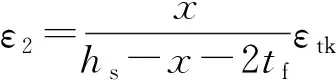
(8)

(9)

由∑X=0得出：

(10)

由∑M=0得到非预应力梁开裂弯矩Mcr2：

(11)

将两者叠加，得到预应力组合梁开裂弯矩Mcr：

Mcr=Mcr1+Mcr2

(12)

利用式(6)～式(12)计算出试验梁的开裂荷载，并与试验值进行对比，结果如表4所示。

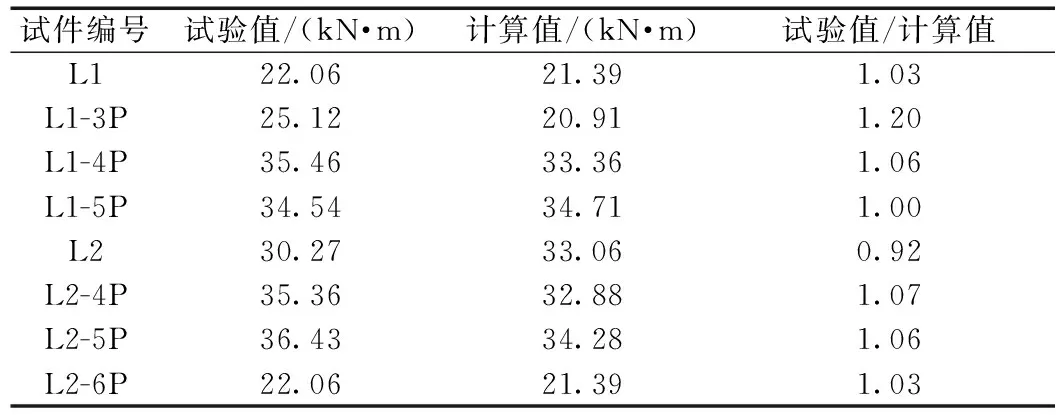
表4 试验值与计算值比较Table 4 Comparison of calculated results with test results

(1)相较于非预应力组合梁L1、L2，2组预应力组合梁开裂荷载均值分别提高42%和23%，说明预应力的存在有效抑制了裂缝开展，极大提升了梁的抗裂性能。

(2)试验梁截面宽高比增大，提高开裂弯矩的效果减弱，主要是因为加大截面宽高比会引起截面刚度的增大，抵抗变形的能力增强，相同条件下，自身抗裂性能得到提高，预应力的影响相对削弱。

(3)弯矩计算法的开裂荷载与试验值非常接近，平均误差在5%左右，证明公式的适用性良好。

4 结论

通过2组试验梁的静力加载试验，对预应力部分外包组合梁的抗裂性能及裂缝规律进行了探究，并提出开裂荷载的计算方法，得到以下主要结论。

(1)未施加应力的部分外包组合梁开裂荷载较小，预应力的施加对提高开裂弯矩有较大作用，但达到一定预应力水平后，效果不明显。适当增大截面宽高比对提高开裂弯矩和承载力有较大影响，且预应力的引入会减弱宽高比对抗裂度的影响。

(2)预应力筋除了可以施加有效预压力外，还能增大截面刚度，使组合梁在开裂后的一定范围内仍能保持较好的弹性工作性能，承担更多的荷载，但增大截面宽高比后，效果会有一定程度削弱。

(3)加载过程中型钢与混凝土存在截面应变差，说明型钢与混凝土的连接存在相对滑移现象，但是截面应变差较小，而且加劲肋有增强作用，可不考虑黏结滑移对组合梁受力分析的影响。

(4)给出的部分外包组合梁开裂荷载计算公式适用性良好，经试验验证是可行的。