基于积分器初值的无人机飞行控制律平滑切换方法

郝现伟，李皓伟，李 铎

(北京宇航系统工程研究所，北京 100076)

0 引言

运载火箭、无人机等飞行器飞行控制系统不仅要完成轨迹制导与姿态控制，还要完成导航和飞行任务管理，是关系飞行器飞行成败的关键系统之一，因此为保证飞行器圆满完成飞行任务，须确保飞行控制系统具有很高的可靠性和安全性[1-2]。

无人机自主飞行过程包括起飞、爬升、定高、下降、下滑、拉平、着陆滑跑等飞行阶段，每个飞行阶段具有不同的控制目标[3]。为保证无人机在每个飞行阶段均具有较好的控制性能，需根据无人机特性及各飞行阶段的控制目标，设计相应的飞行控制律。不同的飞行阶段可能采用不同的控制律，这必然面临着多组复杂控制律之间的切换问题。控制律之间的切换可能会引起舵面瞬间跳变，从而产生较大的力矩，姿态变化剧烈，可能使无人机不可控，因此如何实现多组复杂控制律之间的平滑切换，避免舵面瞬变，是无人机自主飞行控制的关键技术。

对于多模态控制律切换问题，段广仁等[4]基于参数化特征结构配置结果及模型跟踪方法，设计了满足输出跟踪性能并使多模型系统中各闭环子系统逐渐稳定的多模型切换控制律集合，通过协调选取各子系统控制律中的参数来抑制切换时刻的输出跳变，这种方法理论性太强，工程可实现性较差；王元超等[5]基于Stateflow给出了6种飞行模态之间的控制律逻辑切换条件，但没有对不同飞行模态之间控制律平滑切换进行研究。目前，工程上常采用的控制律平滑切换方法有双模态同步运算瞬变抑制法和单模态运算瞬变抑制法[6]。虽然双模态同步运算瞬变抑制法瞬变抑制效果明显，但需要同时运算两种模态的飞行控制律，将占用过多的计算机机时和内存，并且在切换过程中系统的稳定裕度难以确定。单模态运算瞬变抑制法在双模态同步运算瞬变抑制法的基础上做了改进，虽然只须运算当前模态的飞行控制律，克服了双模态抑制法须同时运算两组控制律的缺点，但是切换过程中系统的稳定裕度仍难以确定，并且要根据经验调整淡入淡出时间参数，以达到较好的切换效果。

针对无人机多组复杂控制律之间的平滑切换问题，本文提出基于积分器初值的控制律平滑切换方法。首先将复杂控制律的各个环节进行形式变换，拆分成由比例和积分组成的基本单元结构；然后以舵面平滑切换为目标，由后向前(从舵面指令向给定指令方向)依次递推出复杂控制律中所有积分器的初值，从而实现不同控制律之间的平滑切换。通过算例仿真验证不同控制律之间平滑切换方法的有效性。

1 问题描述

无人机各飞行阶段控制目标不同，控制率也不同，因此需进行多组控制率切换。若多组控制率切换问题处理不当，会引起舵面跳变，可能造成无人机飞行姿态剧烈变化，致使无人机不可控。尤其在进场着陆阶段，无人机会经历下滑、拉平和着陆滑跑，该过程无人机飞行高度和飞行速度逐渐降低，对无人机的接地速度、接地俯仰角、侧偏距等均有较强的约束性[7]，此时采取措施抑制舵面瞬变实现复杂控制律之间的平滑切换，可提高无人机对期望着陆轨迹的跟踪精度，提高无人机的着陆平稳性和安全性。

复杂控制律之间的切换示意图如图1所示。图1中，飞行模态1对应着控制律A，飞行模态2对应着控制律B。控制律A和B为常规的PID控制，由PID控制器和综合校正环节组成。在控制律切换之前，无人机处于飞行模态1，通过运算控制律A得到舵面偏角指令δc=δc1。当满足控制律切换条件后，无人机转为飞行模态2，此时任务管理与控制律调度模块发出指令由控制律A切换成适用于飞行模态2的控制律B，通过运算控制律B得到舵面偏角指令δc=δc2。由此可见，如何保证控制律切换后的第一个运算周期，使经控制律B解算得到的δc2等于前一个运算周期经控制律A解算得到的δc1，是实现两组控制律之间平滑切换的关键研究。

图1 复杂控制律之间的切换示意图Fig.1 Smooth switching between complex control laws

2 飞行控制律平滑切换方法

无人飞行控制律通常为常规PID控制，包括PID控制器和综合校正环节。由数字积分器工作原理[8]可知，在控制律切换后的第一个运算周期，积分器输出值为初值，在之后的运算周期，积分器输出值为初值累加积分器输入值。根据此积分器的特性，在控制律切换后的第一个运算周期，首先将复杂控制律的各个环节进行形式变换，拆分成由比例和积分组成的基本单元结构，然后以舵面平滑切换为目标，由后向前(从舵面指令向给定指令方向)依次递推出复杂控制律中所有积分器的初值，之后再对复杂控制律中所有积分器赋上递推出的初值，即可使经新控制律解算得到的舵偏指令与经前控制律切换前最后一个运算周期解算得到的舵偏指令相等，最终实现两组控制律之间平滑切换。

(1)

拆分后的校正环节Gjz(s)的结构如图2所示。

图2 校正环节拆分后的结构图Fig.2 Diagram of the correction link after split

图2中含有积分器环节。定义yin为校正环节输入值，yout为校正环节输出值，I0为积分器初值。

控制律切换时，以下等式成立

(2)

可推导出积分器初值I0和校正环节输入值yin的表达式

(3)

式中，输出值yout与前一个运行周期的舵面偏角指令有关，即yout=f(δc1)。

PID控制器结构如图3所示。

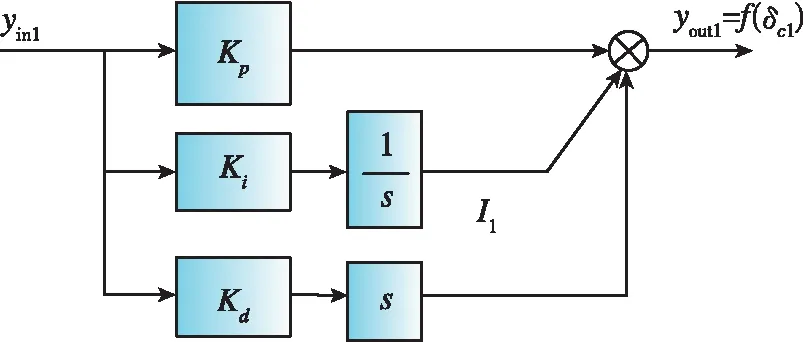
图3 PID控制器结构图Fig.3 PID controller structure

控制律切换时，以下等式成立

(4)

可推导出积分器初值I1的表达式

(5)

式中，输出值yout1与前一个运行周期的舵面偏角指令有关，即yout1=f(δc1)。

控制律切换时刻，已知前一个运行周期舵面偏角指令δc1，则可求得yout，yout1的值，进而根据式(3)，(5)可求得积分器初值I0，I1。

将推导出的积分器初值赋入新控制律中相应的积分器中，在控制律切换后的第一个运算周期经新控制律解算的舵面偏转指令即可与前一个运行周期的舵面偏角指令相等，从而实现不同控制律之间的平滑切换。

3 算例

以某无人机进场着陆为例，对两种飞行模态下升降舵通道不同控制律之间的切换进行分析。

某无人机进场着陆飞行，为增升需要，襟翼将下偏至某规定位置，同时当满足起落架释放条件后，无人机起落架将缓慢放下，该过程称为构型变化。为保证构型变化前后的俯仰通道着陆控制系统均具有较好的控制性能，设计了两组不同的飞行控制律，则必然面临着两组控制律之间的切换问题。控制律之间的切换可能会引起升降舵舵面瞬间跳变，从而产生较大的俯仰力矩，致使飞行器姿态剧烈变化，因此需采用抑制措施，避免舵面瞬变。图4给出了构型变化后的升降舵通道控制结构。

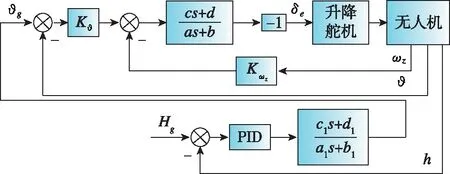
图4 构型变化后的升降舵通道控制结构Fig.4 Control structure of the pitch channel after the configuration change

图4中，PID控制器结构如图3所示，控制律参数包括Kp，Ki，Kd。各控制律参数值如下

Kp=1.5，Ki=0.32，Kd=0.9，Kϑ=2.3，Kωz=1.2，a=1，b=3.11，c=2.16，d=2.31，a1=1，b1=4.84，c1=0.77，d1=2.57

根据第2节提出的基于积分器初值的控制律平滑切换方法，对图4中两个校正环节和PID环节共3个积分器赋初值。用Ih0表示内回路校正环节中积分器的初值，用Ih1表示外回路校正环节中积分器的初值，用Ih2表示外回路PID环节中积分器的初值，已知控制律切换时刻前一个运行周期的舵面偏角指令为δe1，则Ih0，Ih1，Ih2的表达式为

(6)

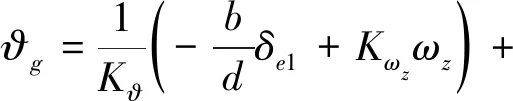
为检验本文提出的基于积分器初值的控制律平滑切换方法的合理性和有效性，以下分别采用双模态同步运算瞬变抑制法、单模态运算瞬变抑制法和积分器赋初值法进行非线性全量仿真对比。记录并给出飞行高度、高度差(正高度差表示期望高度大于实际飞行高度)、升降舵指令、法向过载和俯仰角的响应曲线，如图5所示，图中xd为无人机距理想接地点的水平距离。

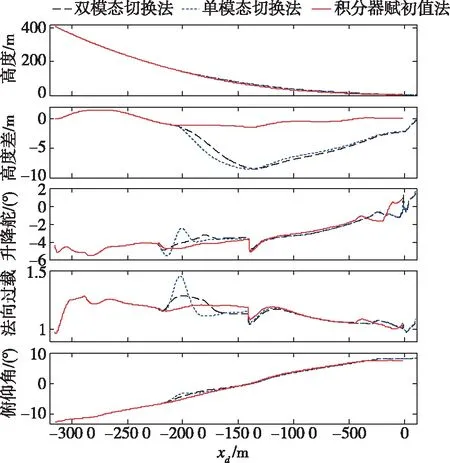
图5 复杂控制律平滑切换仿真对比Fig.5 Simulation comparison of complex control law smooth switching

由图5可见，采用双模态切换法和单模态切换法时，飞行器对期望着陆轨迹的跟踪精度较差(最大高度跟踪误差均近9 m)，着陆飞行过程波动较大(最大法向过载分别为1.32和1.46)，接地散布较大(实际接地点距理想接地点的纵向偏差为98 m)；但采用本文提出的串联递推积分器初值控制律平滑切换方法时，无人机对期望着陆轨迹的跟踪精度最高(最大高度跟踪误差为1.3 m)，实际接地点距理想接地点的纵向偏差最小(仅为-16.3 m)，接地散布最小，着陆飞行过程最平稳(最大法向过载为1.18)。由此可见，本文提出的控制律平滑切换方法是有效的，该方法同时提高了飞行器的着陆平稳性和安全性。

4 结论

对于无人机自主飞行过程中复杂控制律之间切换时出现的舵面瞬变问题，本文提出了基于积分器初值的控制律平滑切换方法，实现了复杂控制律之间的平滑切换，提高了无人机飞行平稳性和安全性。本文提出的控制律平滑切换方法不仅适用于无人机飞行控制系统，还适用于运载火箭、机器人等研究对象的控制系统，具有较高的工程应用价值。