基于神经网络和证据理论的火箭发动机故障诊断

孙成志，闫晓东,2

(1. 西北工业大学航天学院, 西安 710072； 2. 陕西省空天飞行器设计技术重点实验室, 西安 710072)

0 引言

随着航天科技的发展，高可靠性逐渐成为航天发射任务的追求目标。在全箭众多的故障模式中，动力系统故障是运载火箭最常发生、造成后果最严重的故障，轻则使运载火箭入轨精度降低，重则直接导致飞行任务失败[1-2]。因此，研究运载火箭发动机故障诊断具有非常重要的工程价值和实际意义。

运载火箭动力系统模式复杂，建立系统的解析模型十分困难，故障诊断正确率不高[3]。目前，针对运载火箭动力系统故障诊断方法层出不穷，基于信号检测的故障诊断方法[4]、模糊理论的故障诊断方法、专家系统的故障诊断方法以及一些常规的故障诊断方法存在很大的局限性和适用性较差的问题[5]。然而，基于神经网络的故障诊断方法，处理数据能力较强，适合处理数据量丰富的运载火箭发动机数据[6]，同时，神经网络良好的非线性特性也适合对故障模式繁多、故障原因复杂的非线性运载火箭动力系统进行故障诊断[7]。但是神经网络容易陷入局部极小值，有时只能得到局部最优解，可能会出现误诊的情况。在进行故障诊断时，不同故障特征相互混杂在一起会出现多耦合、模糊性等复杂特征[8]，因此不能利用单一的方法判断故障模式。证据理论在无需先验知识的情况下，能够根据自身的算法融合不同方法的结果并以推理的形式获得确定的结果[9]，已经成为故障诊断领域的热点方向。

禹建丽等[10]通过构建BP神经网络、RBF神经网络和GRNN(广义回归神经网络)故障诊断模型对变压器进行故障诊断。张炜等[11]通过建立复杂设备故障诊断的多重神经网络模型结构，将其应用于液体火箭发动机涡轮泵的故障诊断。刘兵等[12]提出了一种基于模糊神经网络的故障诊断方法，较好地解决了固体火箭发动机地面试验系统的不确定故障诊断问题。郝大鹏等[13]运用PNN(概率神经网络)建立故障诊断模型，对汽车尾气进行分析并诊断发动机故障。卢俊文等[14]通过改进L-M算法优化BP神经网络的学习算法，对航空发动机气路故障进行诊断。汪广洪等[9]运用BP网络良好的非线性映射能力和D-S证据理论基本概率分配计算的客观化能力，提出基于BP神经网络和D-S证据理论信息融合的航天器故障诊断方法，但并未给出仿真算例验证。张雷[15]提出一种基于重组粒子群算法的神经网络故障诊断方法，对滚动轴承故障进行诊断。刘小明[16]针对运载火箭的复杂特性以及传统BP算法的收敛速度慢、极易陷入局部极小的缺点和实际的故障样本少的特性，提出了一种基于故障树和SVM算法神经网络的故障智能诊断方法。李化南[6]在BP网络结构的基础上，提出了一种基于BP网络的3层诊断模型，对液体火箭发动机的故障模式进行诊断。

虽然国内外许多学者在故障诊断方面做了很多研究，但是在神经网络的应用层面上，大多数都是使用单个网络进行诊断，之后将各个网络的诊断结果进行对比，这样很容易出现误诊的情况；也有学者将多个网络融合，但是诊断网络较为简单，只适用于已经存在的故障模式，对于未参与网络学习的故障模式无法诊断，并且无法估计故障模式下具体的特征参数。因此本文提出了基于神经网络和证据理论的方法对运载火箭发动机故障模式进行诊断，并通过滚动时域估计方法对运载火箭飞行状态特征量进行估计，对于未参与网络学习的故障模式也能达到很好的诊断效果。首先采集运载火箭的视加速度和角速度信息；之后通过归一化神经网络输入数据，将不同故障模式标签化并对神经网络进行训练，建立用于运载火箭发动机故障诊断的神经网络模型；接着通过D-S证据理论融合BP神经网络和RBF神经网络的诊断结果，判断最终的故障模式;最后在确定故障模式的情况下利用滚动时域估计方法，估计运载火箭发动机故障下的飞行状态特征量。

1 BP神经网络

BP神经网络是一种按照误差反向传播算法训练的多层前馈网络。主要由输入层、隐含层和输出层组成[17]，其结构如图 1所示。

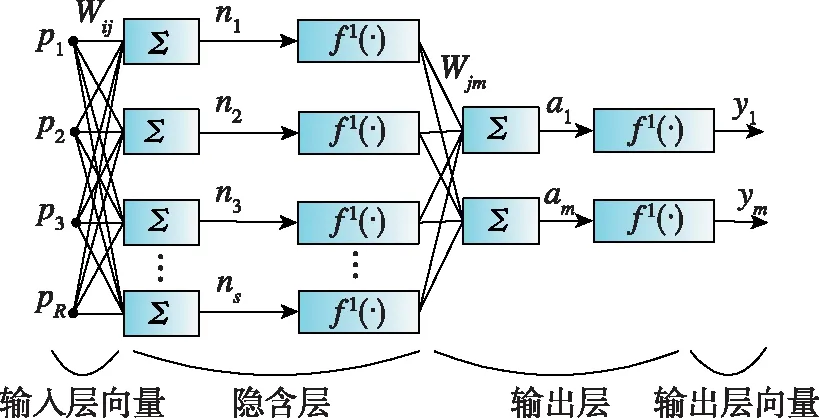
图1 BP神经网络模型结构Fig.1 Model structure of BP neural network

BP神经网络学习包括信号的前向传播和误差的反向传播两个过程[18]。

BP网络三层节点表示为：输入节点xj，隐节点yi，输出节点Ol。输入节点与隐节点间的网络权值为ωij，阈值为θi；隐节点与输出节点间的网络权值为Tli，阈值为θl；输出节点的期望输出为tl。

BP算法的步骤如下[19]：

1)设置各个权值和阈值的初始值；

2)利用式(1)，(2)计算隐含层和输出层的输出

yi=f(∑ωijxj-θi)

(1)

Ol=f(∑Tliyi-θl)

(2)

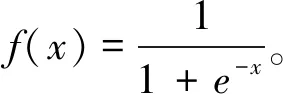
3)计算输出节点与期望输出之间的误差

(3)

4)按照公式更新各权值和阈值

Tli(k+1)=Tli(k)+η(tl-Ol)Ol(1-Ol)yi

(4)

(5)

θl(k+1)=θl(k)+η(tl-Ol)Ol(1-Ol)

(6)

(7)

其中，η为学习效率。

5)重新计算各层的输出值，当误差小于目标误差时训练完成，否则重复上述步骤更新权值、阈值，直至达到制定精度或者达到指定训练次数。

BP神经网络学习流程如图 2所示。

图2 BP神经网络学习流程Fig.2 Learning process of BP neural network

2 RBF神经网络

如图 3所示，RBF由单隐层的三层前馈网络构成，其中隐藏层中神经元的变换函数。

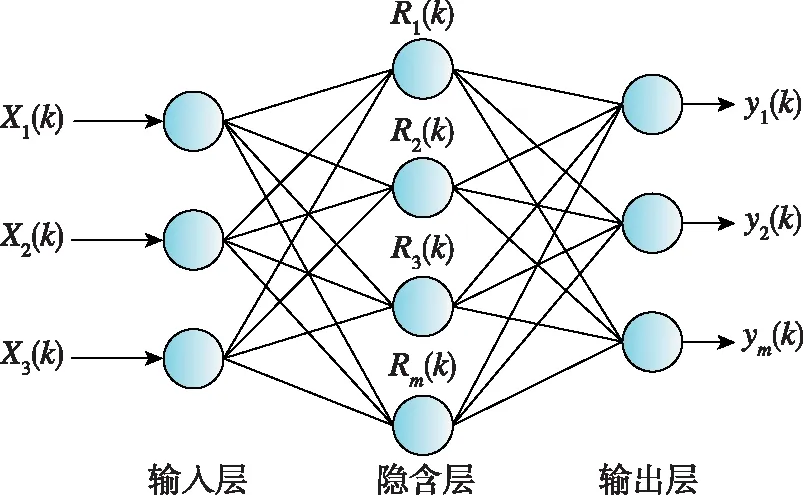
图3 RBF神经网络模型结构Fig.3 Model structure of RBF neural network

RBF神经网络学习过程中，首先采用无监督学习确定隐含层中心、扩展常数，最后通过梯度下降法训练权值[20]。

假设t为迭代次数，则第t次迭代时聚类中心μ1(t),μ2(t),…,μk(t)，相对应的聚类域为W1(t),W2(t),…,Wk(t)。采用K-means聚类算法确定 RBF 神经网络隐含层的中心和扩展常数的步骤如下[21]：

1)根据算法应用环境初始化K个聚类中心，每个聚类中心的维度和输入数据的维度保持一致；

2)通过式(8)计算训练样本与聚类中心的距离dk，j

(8)

其中，k=1,2,…,K;j=1,2,…,N，N为样本长度。

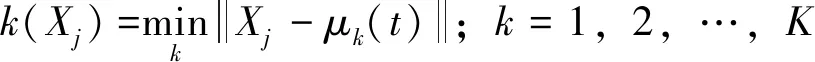
4)通过式(9)计算新的聚类中心

(9)

其中，k=1,2,…,K;Nk为第k类中的样本个数。

5)如果μk(t+1)≠μk(t)，转到第2)步，否则聚类结束，转第6)步执行；

6)根据式(10)计算RBF神经网络隐含层神经元的扩展常数

σ=κdk

(10)

其中，κ为重叠系数，dk为第k个数据中心与其余K-1个数据中心距离的最小值，即

(11)

通过K-means聚类算法确定隐含层神经元中心和扩展常数得到网络输出权值后，通过梯度下降法训练网络权值。基于梯度下降的权值训练算法[21]为：

RBF神经网络学习的目标函数为

(12)

其中，κj为遗忘因子，误差信号ej定义为

(13)

考虑所有训练样本和遗忘因子的影响，μk，σk和ωk的调节量为

(14)

(15)

(16)

其中，φi(Xi)为第k个隐节点对Xj的输出，η为学习率。

3 D-S证据理论

D-S证据理论建立在一个非空集合Θ上，Θ称为辨识框架，在航天器故障诊断中，Θ为一个故障模式对应的基本故障组成的集合[22]。

定义基本概率分配函数BPAF(Basic Probability Assignment Function)

m:2Θ→[0,1]

其中，m满足

m(Φ)=0

(17)

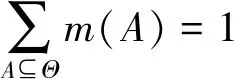
(18)

(A,m(A))称为证据体，利用证据体定义信度函数和似然函数

(19)

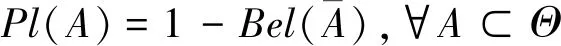
(20)

Bel和Pl表示信度函数上的上下限值，称为信度区间[23]，如图 4所示。

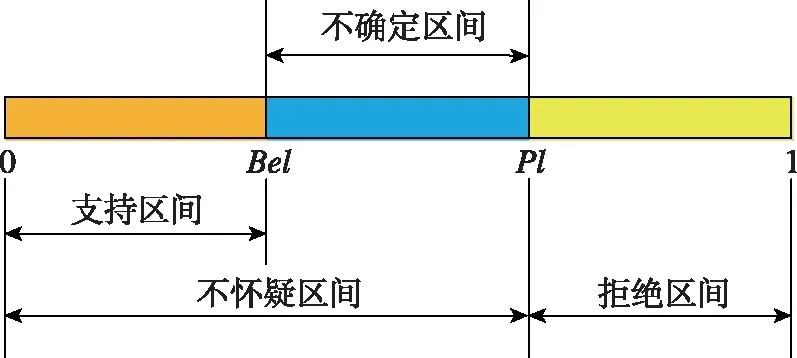
图4 命题不确定度Fig.4 Uncertainty of proposition

D-S合成规则是在相同的识别框架下，给定不同证据的信度函数，运用合成法则计算各个证据融合之后的信度函数。

设Bel1和Bel2分别为同一识别框架上的两个基本概率赋值分配，基本元素分别为A1,A2，…,AK和B1,B2，…,BK，则组合后的基本概率赋值为

(21)

其中，K为冲突因子。

(22)

该合成规则通过融合多个证据体，可以降低各个命题之间的冲突，提高诊断结果的精确性。

4 滚动时域估计

滚动时域估计(Moving Horizon Estimation，MHE)可以将估计问题转为优化问题，同时将系统的约束条件描述在优化问题中，通过在线滚动优化使其动态满足[2]。

考虑如下类型的线性离散系统

Xk+1=AXk+GWk

(23)

Zk=CXk+Vk

(24)

其中，Xk为系统状态，Zk为测量输出，Wk为系统噪声，Vk为量测噪声，A为状态转移矩阵，G为输入矩阵，C为量测矩阵。

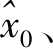
(25)

满足约束式(26)～(28)。

xk+1=f(xk,uk,wk,k)

(26)

yk=h(xk,k)+vk

(27)

xk∈Xk,wk∈Wk,vk∈Vk

(28)

其中，h(xk,k)为非线性的观测函数。

通过引入固定的数据时域，可以将带约束优化问题的计算时域分为两个部分

{t1:0≤k≤T-N-1}和{t2:T-N≤k≤T-1}，目标函数定义为式(29)

(29)

定义到达代价函数为式(30)

(30)

其中，极小化问题满足约束式(26)～(28)。在此基础上根据前向动态规划原理，可以将优化问题等价为式(31)

ΘT-N(xT-N))

(31)

并且

(32)

满足约束式(26)～(28)，N为滚动时域窗口长度。

对于非线性目标运动模型，使用扩展卡尔曼滤波和滚动时域估计算法得到目标的状态估计[25]。

扩展卡尔曼滤波的状态估计和状态估计的协方差矩阵的递推估计方程如式(33)，(34)

(33)

(34)

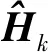
基于扩展卡尔曼滤波的滚动时域估计的状态估计递推方程如下

(35)

其中，T为当前仿真时刻。

5 基于证据理论融合和滚动时域估计的诊断模型

5.1 神经网络诊断模型

神经网络的训练误差是一个不确定因素。网络输出节点的输出被归一化处理为焦点元素的基本概率值并代入计算公式

(36)

其中，fi表示故障模式，y(fi)表示神经网络的输出结果，En表示神经网络样本误差。

由于发动机的构型和参数是固定的，因此，在飞行前可以建立一系列的故障模式，并建立其特征参量模型，这些作为在线轨迹的先验信息。通过对飞行状态的观测来估计发动机故障模式。神经网络的输入选取为运载火箭的箭体坐标系下的三轴视加速度和三轴角速度，为了满足网络对输入输出的要求，须在训练开始之前对数据进行归一化处理；输出选取运载火箭的故障模式矩阵。建立故障类型矩阵如表 1所示。

5.2 证据理论融合诊断模型

由BP神经网络、RBF神经网络和D-S证据理论决策融合系统组成的运载火箭发动机故障模式融合诊断系统如图 5所示。

识别框架为

Θ=(ENG11，ENG12，ENG13，ENG14，ENG15，ENG21，ENG22，ENG23，ENG24，ENG25，ENG31，ENG32，ENG33，ENG34，ENG35，ENG41，ENG42，ENG43，ENG44，ENG45)。

定义一种新的基本函数构建方法，以式(37)作为基本概率函数

(37)

m(Θ)=En

(38)

C(Ai)为BP神经网络和RBF神经网络的初步诊断结果，m(Θ)为证据体的不确定性表示，N为故障类型数，En表示BP神经网络和RBF神经网络诊断结果与期望值的均方差。

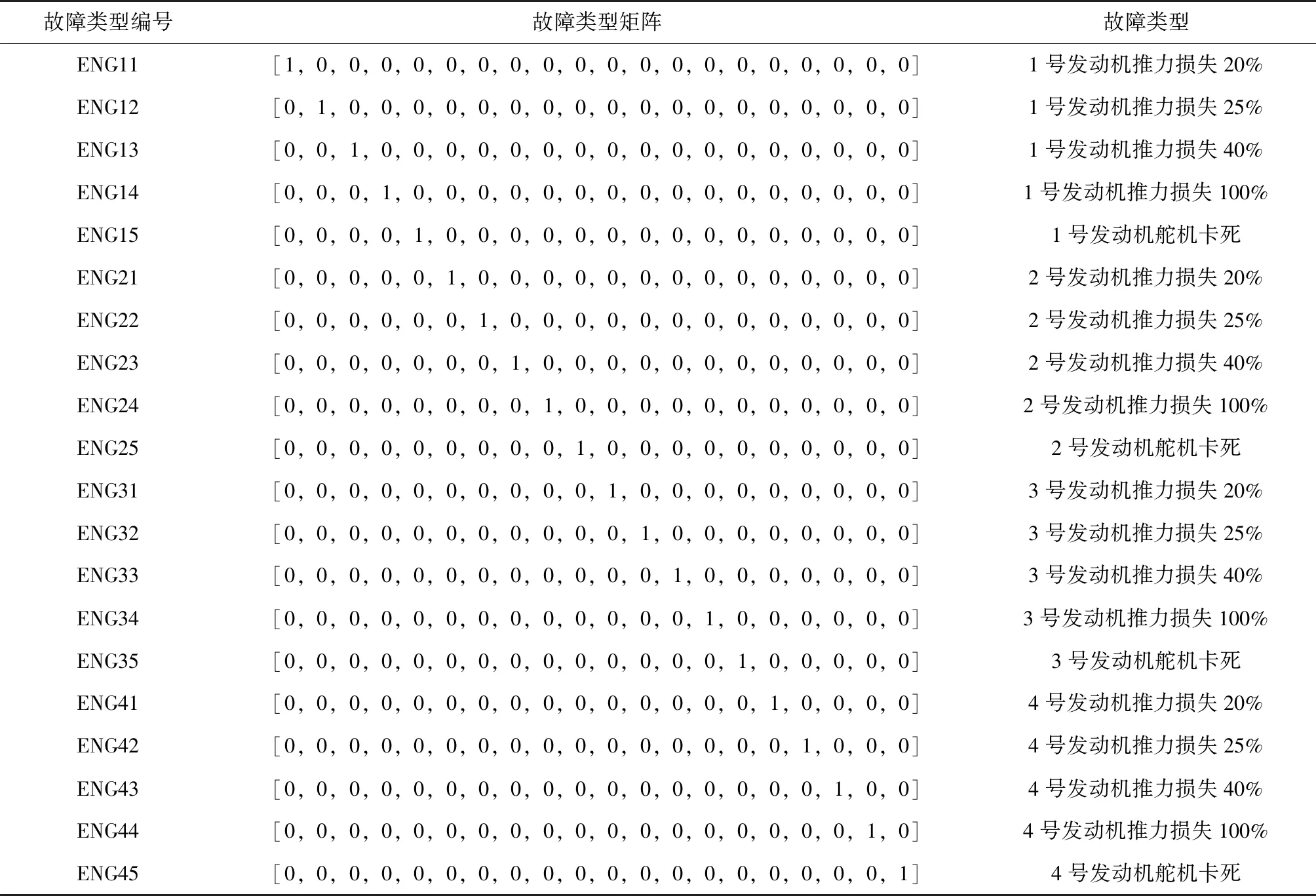
表1 故障类型矩阵

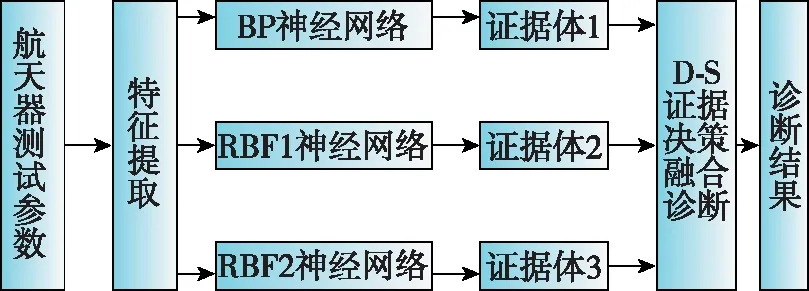
图5 火箭故障融合诊断系统Fig.5 Fusion diagnosis system of rocket fault

5.3 滚动时域估计算法模型

系统的状态向量为

分别为运载火箭在发射坐标系下的加速度、角速度、速度以及位置。

量测向量为

分别为运载火箭弹体坐标系下的三轴视加速度。

单个发动机推力损失量

Ploss=Pc-Pr

(39)

其中，Pc为发动机当前总推力，Pr为发动机额定总推力。

单个发动机推力损失百分比

(40)

6 仿真算例

6.1 BP网络诊断结果

仿真生成8 000组不同故障模式下的数据，利用6 000组数据作为训练样本，2 000组数据作为检测样本。

选取BP神经网络精度为0.001，网络学习率为0.5，最大训练次数为300次。隐含层神经元个数为128的训练效果如图 6所示。

图6 BP神经网络训练效果Fig.6 Training performance of BP neural network

对2 000组测试数据使用训练好的BP神经网络诊断，诊断正确率为99.1%。

6.2 RBF网络诊断结果

选取RBF神经网络的目标精度为0.01，网络传播速度为1，最大训练次数为500次。训练效果如图 7所示。

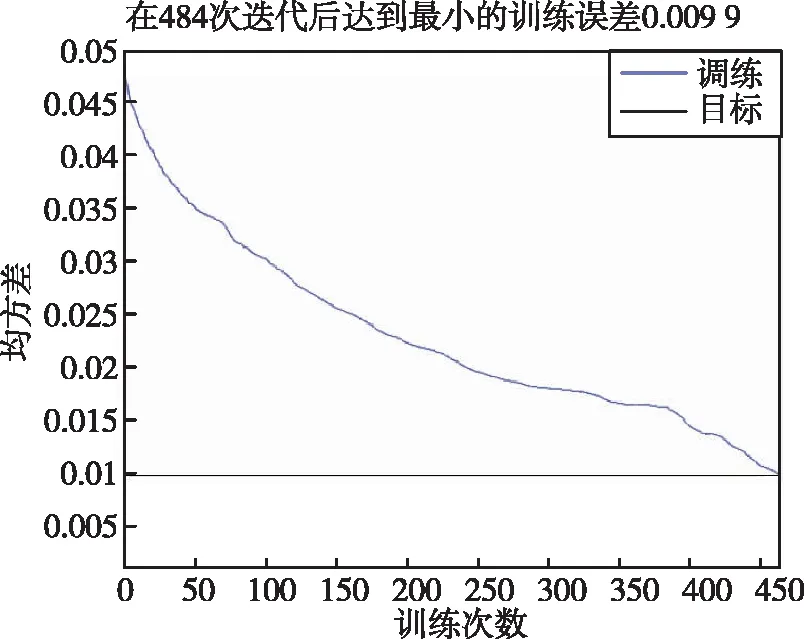
图7 RBF神经网络训练效果Fig.7 Training performance of RBF neural network

对2 000组测试数据使用训练好的RBF神经网络诊断，诊断正确率为99.2%。

6.3 融合诊断算例

算例1：

假设故障模式为ENG44，运载火箭发动机在100 s时，芯一级四号发动机推力下降100%，首先通过神经网络和证据理论综合决策，判断运载火箭发动机的故障模式，其次通过滚动时域估计对运载火箭推力损失进行估计。

仿真得到100.01 s时，运载火箭的三轴视加速度和三轴角速度数据如表 2所示。

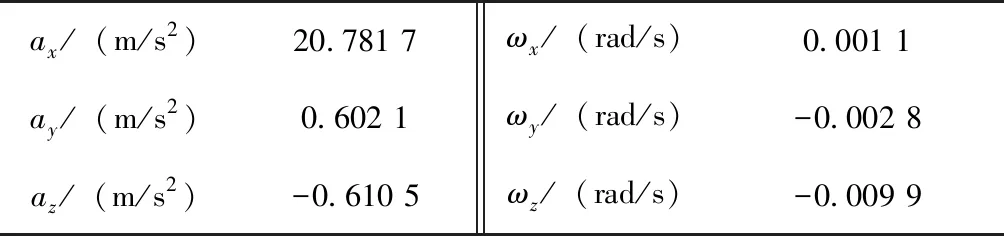
表2 100.01 s时运载火箭部分量测数据

滚动时域估计窗口长度N=4。

利用神经网络进行故障模式诊断，神经网络输出结果如表 3所示。

表3 算例1的神经网络输出结果

对神经网络的输出结果分析，得到火箭故障模式辨识结果如表 4所示。

表4 算例1的神经网络诊断结果

从表 4可以看到，这组测试数据采用BP神经网络进行诊断时出现误诊。从诊断结果的可靠性角度思考，采用不同的神经网络会有不同的诊断结果，不能确定哪种方法的诊断结果是正确的，因此使用D-S证据理论融合诊断结果，确定运载火箭故障类别。首先构建证据体，将ENG44故障状态下的神经网络结果处理得到基本概率分配，经D-S证据理论融合诊断后，结果如表 5所示。

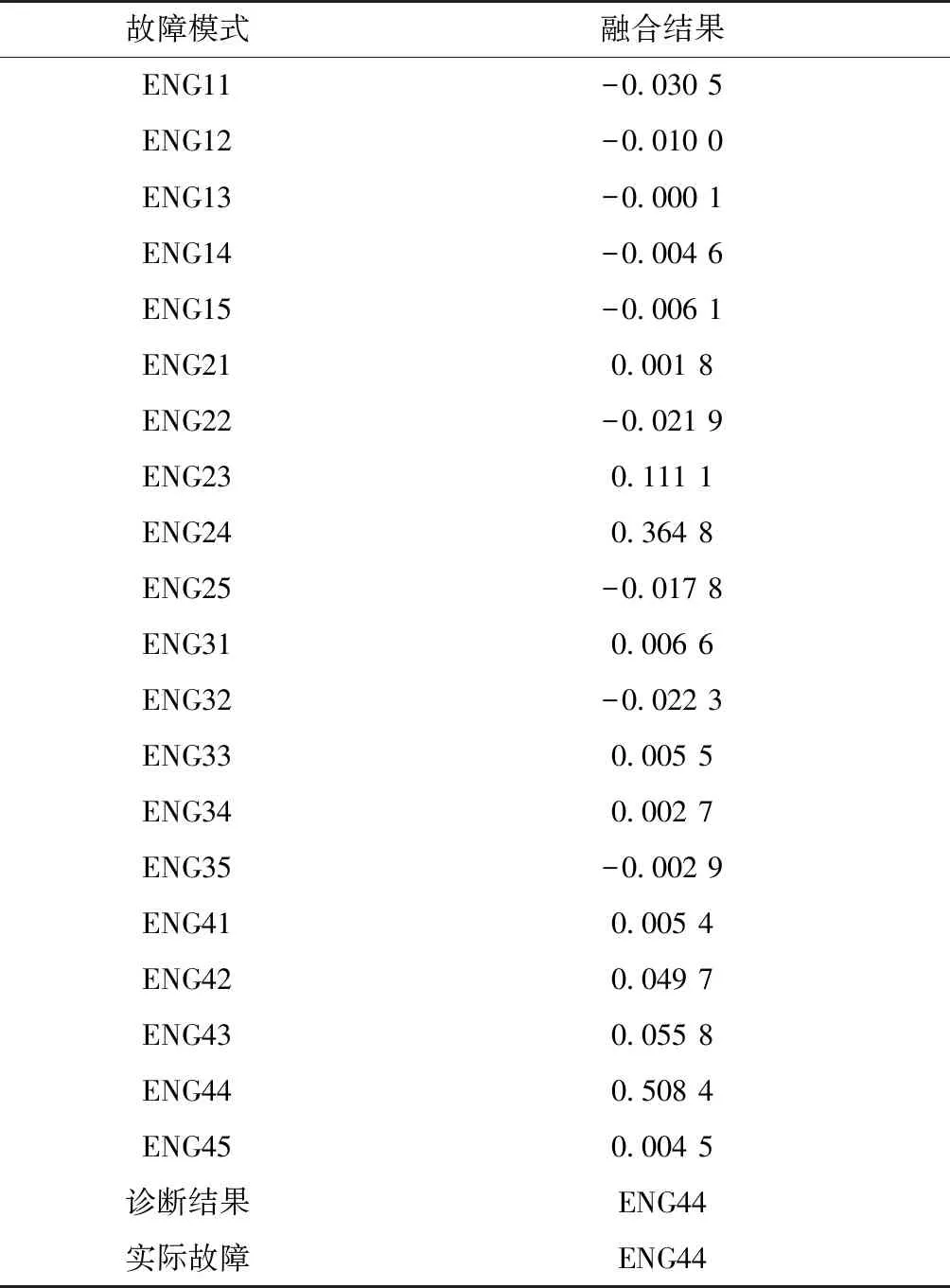
表5 算例1的证据理论融合诊断结果

从表 5可以看出，采用D-S证据理论融合的诊断结果与实际故障模式一致。基于滚动时域估计的运载火箭飞行状态特征量估计的仿真结果如图8～14所示。

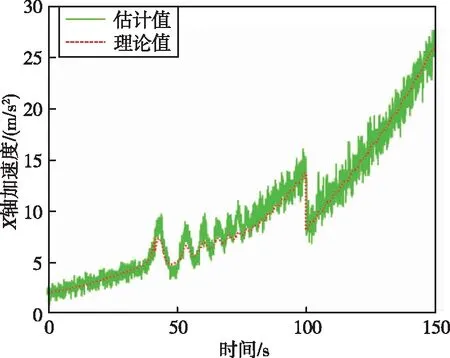
图8 箭体系下X轴加速度Fig.8 X-axis acceleration in the body coordinate system

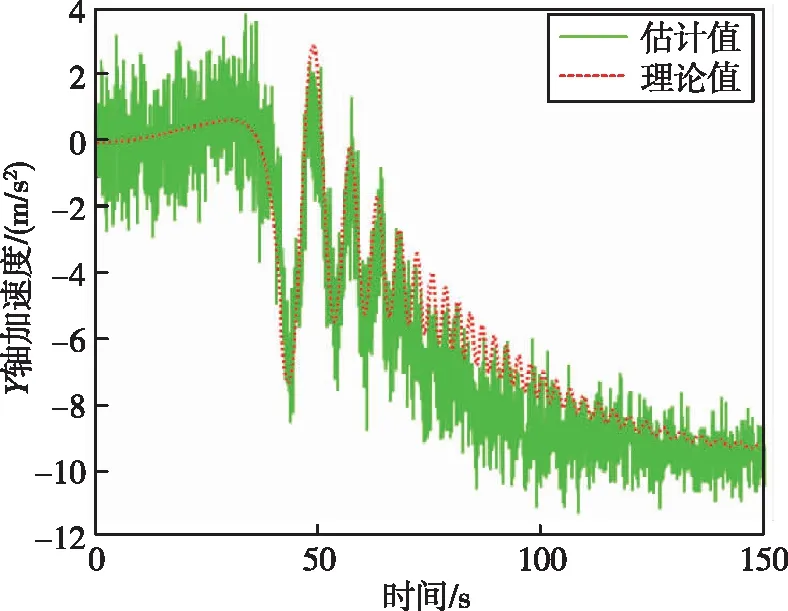
图9 箭体系下Y轴加速度Fig.9 Y-axis acceleration in the body coordinate system

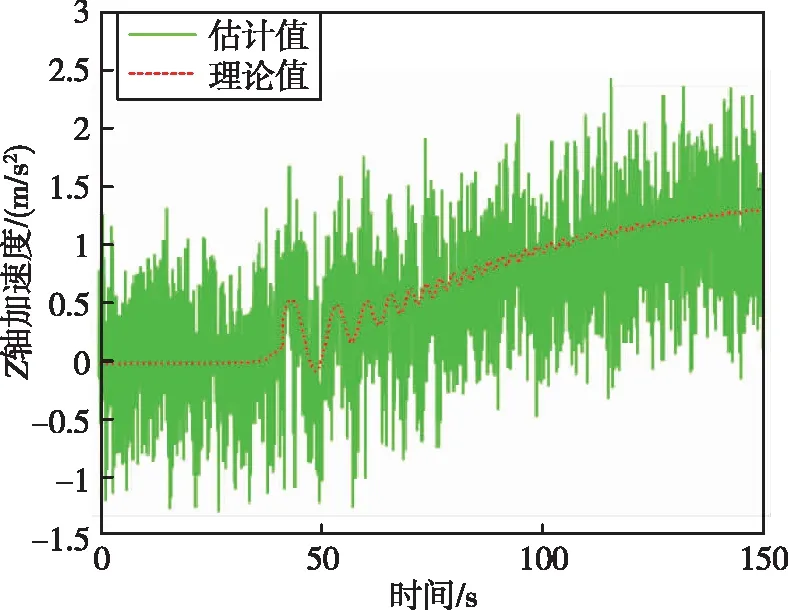
图10 箭体系下Z轴加速度Fig.10 Z-axis acceleration in the body coordinate system

图11 箭体系下X轴角速度Fig.11 X-axis angular velocity in the body coordinate system

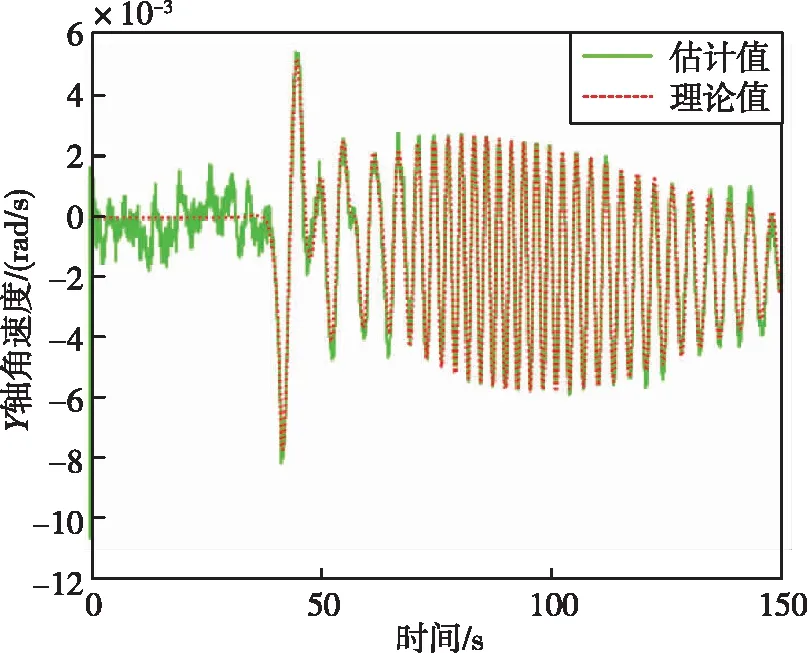
图12 箭体系下Y轴角速度Fig.12 Y-axis angular velocity in the body coordinate system

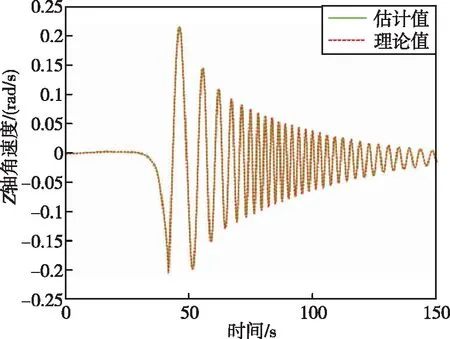
图13 箭体系下Z轴角速度Fig.13 Z-axis angular velocity in the body coordinate system

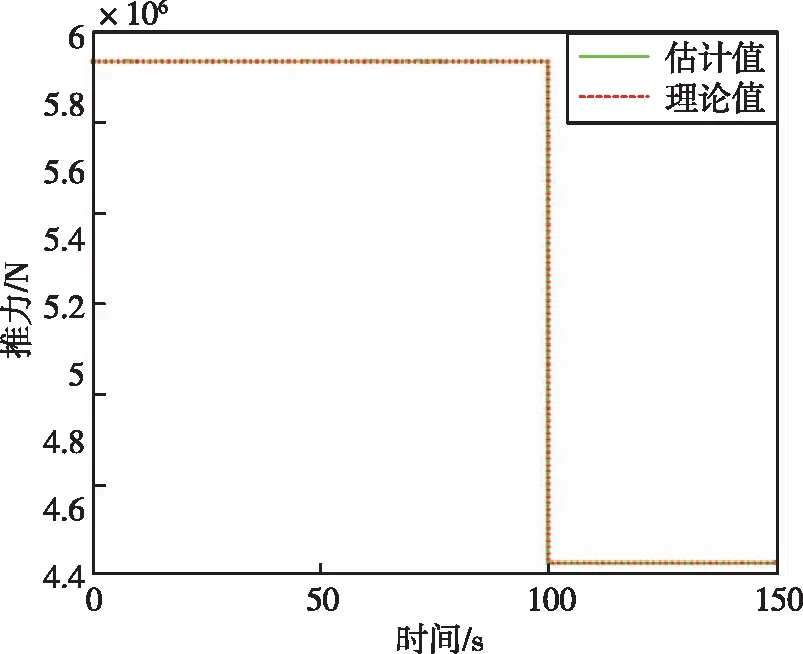
图14 运载火箭总推力Fig.14 Total thrust of rocket

通过图 8～13可以看出，滚动时域估计方法能够很好地估计出运载火箭故障模式下的三轴加速度以及三轴角速度。通过图 14可以看出，在100 s时，运载火箭总推力下降了25%，综合通过证据理论和神经网络得到的运载火箭发动机故障模式，可以判断运载火箭故障类型为四号发动机在100 s时推力下降了100%，符合仿真设定的故障模式。

算例2：

假设故障模式为ENG15，运载火箭在80 s时，芯一级一号发动机舵机卡死，通过神经网络和证据理论综合决策，判断运载火箭发动机的故障模式。

仿真得到80.01 s时，运载火箭的三轴视加速度和三轴角速度数据如表 6所示。

表6 80.01 s时运载火箭部分量测数据

利用神经网络进行故障模式诊断，神经网络输出结果如表 7所示。

表7 算例2的神经网络输出结果

对神经网络的输出结果进行分析，得到火箭故障模式辨识结果如表 8所示。

表8 算例2的神经网络诊断结果

从表8可以看到，这组测试数据采用RBF2神经网络进行诊断时出现误诊，进而使用D-S证据理论融合诊断结果，确定运载火箭故障类别。首先构建证据体，将ENG15故障状态下的神经网络结果处理得到基本概率分配，经D-S证据理论融合诊断后，结果如表 9所示。

表9 算例2的证据理论融合诊断结果

从表9可以看出，采用D-S证据理论融合诊断的故障模式与实际故障模式一致。

基于神经网络和D-S证据理论，对2 000组测试数据进行检测，辨识正确率为99.4%。

7 结论

本文以运载火箭动力系统故障为背景，研究了基于BP神经网络和RBF神经网络的运载火箭发动机故障模式诊断方法，并提出通过D-S证据融合理论综合神经网络的诊断结果，确定故障类型后通过滚动时域估计方法估计火箭飞行状态特征量。通过仿真案例表明神经网络对于故障模式的辨别有较高的正确率，再通过证据理论能够有效提高诊断的准确率，滚动时域估计方法能够在线估计火箭飞行状态特征量，以便对火箭故障进行更精准的判断。该方法还可应用于运载火箭其他模式的故障诊断中，为火箭故障诊断提供了新方法。