数学阅读理解题的特征及教学策略研究
张雪梅


[摘 要] 在新课改的环境下,对学生的阅读理解能力提出了更高的要求. 掌握好阅读理解综合题的解题方法,不仅对中考成绩的高低起到了关键性的作用,同时还培养了学生自主学习能力,使得数学素质教育这一目标落到实处.
[关键词] 阅读理解;综合能力;教学策略
实施新课程标准后,各地中考加强了对阅读理解综合能力的考查,也就是加强了对数学阅读能力的考查,这种考查是全方位的,体现了考查的综合性,促进了数学教学改革的深化. 事实上,不少学生和教师依然习惯性地认为,阅读是语文和英语学科需要的,与数学关系不大,数学学习只是公式与法则的记忆和应用,事实上,这种想法是片面的,也是有偏差的. 为此笔者通过剖析阅读理解这类问题的特征以及考查作用,并结合日常教学经验提出解决阅读理解题的策略,以供参考.
阅读理解题的特征及考查作用
通过深入分析中考阅读理解题,不难看出,中考阅读理解题型大多以解答题为主,相对而言选择与填空题中较少,究其根本在于选择和填空题型大多是对学生定义类问题的考查,而解答题的考查范围则更全面,通过考查此类问题,可以清晰展示学生的数学思维,提升学生的阅读理解能力.
阅读类题型在内容结构上一般可分为以下四个部分:情境引入、迁移理解、应用尝试、延伸探究. 事实上,编者设计此类题型,一般不会明显标注其一般结构,但在结构上却大同小异.
例1 一次数学竞赛中,红红对某一问题进行以下探究.
情境引入:已知如图1所示的四边形ABCD中,有AD∥BC,且点E平分边CD,连接AE并延长与BC的延长线交于点F,证明:S=S.
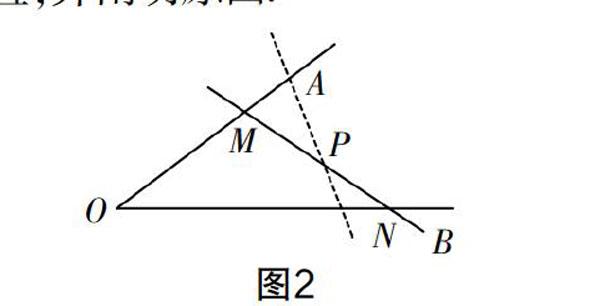
迁移理解:已知如图2所示的锐角AOB内有一定点P,过点P任意作一直线MN,与射线OA交于点M,与射线OB交于点N. 红红把直线MN绕定点P进行旋转,在旋转的过程中她发现S存在最小值. 试求出S最小时直线MN的位置,并阐明原因.
应用尝试:如图3所示,在公路OA和OB之間有一个村庄Q. 某日,村庄Q暴发疫情,防疫防控部门快速投入增设隔离线. 现计划以公路OA和OB以及经过防疫站P的一条直线MN为隔离线,建立一面积最小的隔离区△MON. 经测量,∠AOB=66°,∠PON=30°,OP=4 km,试求△MON的面积.
延伸探究:已知如图4所示的平面直角坐标系中,点O为坐标原点,且点A,B,C,P的坐标分别是(6,0),(6,3),,,(4,2),直线l经过点P且与四边形OABC的一组对边相交,并将四边形OABC分为两个四边形,试求出其中以点O为顶点的四边形的面积最大值.
例2 已知两个相似三角形,当沿着周界并按对应点顺序环绕的方向相同,则可以称这两个三角形互为顺相似;当沿着周界并按对应点顺序环绕的方向相反,则可以称这两个三角形互为逆相似.
(1)图5中的(a)(b)(c)满足条件,可以得出以下三对相似三角形:①△ADE和△ABC;②△GHO和△KFO;③△NQP和△NMQ. 那么,以上相似三角形中,互为顺相似的有______,互为逆相似的有______.
(2)如图5(c)所示,已知锐角三角形MNQ中,有∠M<∠N<∠Q,且点P为三条边上不与三个顶点重合的一点. 过点P作直线PQ截△MNQ,使得截取的其中一个三角形与△MNQ互为逆相似. 试探索不同点P位置所作的截线PQ,画图并阐述截线满足的条件.
上述例1与例2均为中考考题,也是综合性的阅读理解题,例1标出了阅读理解题型的结构特征,而例2虽未标出明显结构,但在内容结构上也是显而易见的,这样的题型主要是对学生的自主学习能力、创新能力和应用能力等多种关键性能力的综合考查.
因此,需要我们在教学上不断引导学生关注,同时促使学生逐步养成自主学习方式. 其实,通过阅读理解问题的解决不仅可以培养学生的能力,在解题思路的发散上也有着非常重要的作用. 这类题型的应运而生为学生思维能力的发展提供了一个很好的平台,为积累丰富的数学活动经验找寻到一个适宜的路径.
■ 阅读理解题的教学策略
解决阅读理解题型并非一蹴而就的,需要广大数学教师探究到一条行之有效的教学策略,并将其一以贯之,由此提升学生的解题能力,同时为教学改革提供助力.
1. 关注知识的形成过程,聚焦学生思维
阅读理解型问题,需要学生通过阅读去感知其中蕴含的数学本质,既要做到细致阅读,同时需充分理解. 因此,知识的形成过程对于学生的学习相当重要,教师需要舍得花时间为学生提供独立思考、动手实践、自主探究和合作讨论的机会,聚焦学生思维的发展,充分领悟数学本质,从而促使学生深度学习,而这些体验、方法以及策略将成为学生解决数学问题的载体.
例如,在学习到“统计”这一章节时,其中方差的知识较为简单,也容易学会,不少教师直接抛出方差的概念,这样的教学过程仅仅是识记的过程,这样的灌输式教学方式显然是不可取的. 笔者在执教这一内容时,出示以下问题:样本甲:6,4,5,4,6,样本乙:3,7,2,8,5,==5,通过观察与思考,学生认识到这些平均数指标尽管无法全面反映其异同,但可以给人带来波动性不同的感知. 进一步,学生发现并提出问题“导致平均数无法反映其波动的原因是什么?”再深入观察数据,可以得出样本甲的偏差情况为“1,-1,0,-1,1”,样本乙则为“-2,2,-3,3,0”,从而得出:其中的正负偏差可以相抵的情形,使得平均数指标无法反映其波动这一特征. 此时学生再一次提出问题:如何克服这样的正负相抵呢?如何将其偏差情形反映出来呢?这样一来,平方手段的“方差”定义就应运而生了.
以上教学过程,重视概念的形成,给予学生充分的自主权,有效锻炼学生的思维能力,帮助学生在头脑中建立起完整的数学知识的理解图式,为自主学习能力的提升奠定良好的知识基础.
2. 深入挖掘教材,渗透思想方法
教材是教师实施教学的蓝图. 在教学过程中,教师需深入挖掘教材内涵,完美地融入数学思想方法,带领学生有深度地学习,有广度地探究,使教与学实现高度统一,全面提升学生的数学综合素养,更好地掌握数学学习的精神.
例如,教学“圆周角定理”时,执教者有意识地联系圆心角进行施教,从中找寻到其对应的圆心角,并通过圆的特性和三角形外角性质去完善教学路径. 在这个过程中,教师没有直接抛出圆心在其角的内、外以及边上的几种情形,更没有直接证明其圆心在边上的这一特例. 不少学生仅仅思考到圆心在圆周角内部这一情况,并进行证明. 此时,执教者通过点拨让学生发现其中的各种关系,同时抛出问题:圆心在圆周角内部的这种证法可以适用于其他情况吗?如果不能,又该如何处理?至此,分类讨论的思想方法自然渗透,同时引出了从特殊到一般的思想方法.
3. 组织适度训练,提升解题能力
阅读理解综合题作为一种新型问题,是在能力立意的思想原则下推出的,教材中自然甚少出现. 那么,教师只有通过自主适度训练,才能帮助学生提升解题能力.
首先,应引导学生快速阅读,留意其中的事件情境、关键词句等细节,从而在头脑中形成初步印象,把握问题的大意;接着,仔细阅读,注意题中的关键数据,并关注到数据间的内在关联,读懂题目,读“薄”问题;然后,从之前提炼而得的信息中进行联想,选用恰当的数学模型和数学思想方法,总结信息;最后,回过头去重新审视问题,仔细研读题中未用数据、关系,同时思考对关键词句的理解是否到位,及时发现问题和解决问题.
总之,教师需灵活将阅读理解综合题的教学融入日常教学中去,充分挖掘现有的教学资源,让学生不仅掌握解决这一类问题的技巧和方法,同时学会用数学的眼光看待和解决问题,使得自身的创新能力得到充分发挥,建构充满生机的数学课堂.

