多约束螺旋机动变结构制导律设计①

段安娜，闫循良

(西北工业大学 航天学院，西安 710072)

0 引言

上述文献对机动制导的实现给出了可行方案，但均未考虑落角、入射方位角和速度等约束对打击任务的限制。本文以大升阻比高超声速滑翔飞行器为对象，设计了一种综合考虑机动突防与打击精度的多约束机动制导策略与方法。该方法保证了进攻飞行器以高超声速俯冲的同时做螺旋机动，反导系统将被置于极短反应时间的境地之中，拦截弹在拦截对抗过程中，过载易饱和，因而能较大程度提高进攻飞行器的突防概率；在飞行末段，进攻飞行器不再机动，以全力保证终端制导精度和约束满足情况。

1 运动建模

高超声速滑翔飞行器为大升阻比面对称外形，采用BTT控制方式。俯冲攻击阶段，飞行时间短，飞行高度低，可以忽略地球扁率和自转的影响。假设滑翔飞行器随时处于“瞬时平衡”且控制系统理想工作，可建立滑翔飞行器的三自由度运动模型。

(1)

式中V、θ、ψv分别为速度大小、弹道倾角和弹道偏角；x、y、z分别为滑翔飞行器的位置坐标；t为时间，微分自变量；m为滑翔飞行器总质量；X、Y分别为气动力在速度坐标系上的分量，即阻力和升力；gxh、gyh、gzh分别为重力加速度在弹道坐标系下的投影。

气动力X、Y由以下等式确定:

X=CxqS

Y=CyqS

(2)

式中q为动压；S为滑翔飞行器的参考面积；Cx、Cy分别为阻力系数和升力系数，其中隐含了控制参数攻角α，另一个控制参数为速度倾侧角γv。

下面采用双平面解耦的方法，将俯冲段相对运动分解到俯冲平面和转弯平面上，建立寻的制导问题的相对运动方程。首先，对飞行器在转弯平面上的运动情况进行分析。

转弯平面上的运动方程可表示为

(3)

式中R为目标与飞行器的相对距离；Vt为目标速度大小；Vm为飞行器速度大小；qtt为视线在转弯平面上的视线方位角；γtm为飞行器速度矢量在转弯平面上的方向角；γtt为目标速度的方位角。

为方便表示，令

(4)

对式(3)中的两个方程左右两边同时求导：

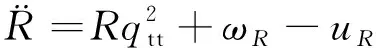
(5)

(6)

当目标固定时，Vt=ωR=ωq=0，式(6)可化简为

(7)

俯冲平面内运动建模与转弯平面类似。注意到俯冲平面内滑翔飞行器速度与视线的夹角为qd+γdm(γdm<0)，可得到在俯冲平面内的运动方程为

(8)

综上所述，可得高超声速滑翔飞行器与静止目标间的相对运动方程：

(9)

式中qd为视线在俯冲平面上的视线高低角；qtt为视线在转弯平面上的视线方位角；γdm和γtm分别为速度矢量在俯冲平面和转弯平面上的方向角。

2 多约束螺旋机动滑模变结构制导律

2.1 俯冲平面制导律设计

为使相对运动系统对参数摄动和外界干扰具有鲁棒性，考虑采用变结构控制理论设计制导律。在保证零脱靶量的基础上，加入视线角参考指令约束和机动运动控制项qdn，将滑动模态设计为

(10)

(11)

式中γdf为期望落角；λ为角误差项系数；cdn为正弦机动的机动幅度设计参数；kdn为机动频率设计参数；h为当前飞行高度；h0为初始射高。

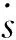
(12)

式中k为趋近律系数；ε为切换项增益，均为大于0的常数。

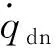
(13)

2.2 转弯平面制导律设计

与俯冲平面类似，采用相同的趋近律，同时设计转弯平面上的滑动模态和机动运动控制项分别为

(14)

(15)

同理，可得转弯平面上的多约束螺旋机动变结构制导律为

(16)

可看出，由于角度正负的规定略有不同、滑模面的选取不同，两个平面上制导律有所区别。

2.3 抗抖动改进

由于式(13)和式(16)含有非连续的开关函数项，即需要控制量进行跳变切换，而在实际工程中瞬时切换是无法实现的，总会有时间滞后发生，这就导致了抖动现象的产生。为削弱控制量抖动，需要对非连续开关函数进行光滑处理。本文用饱和函数sats代替符号函数sgns，即在边界层φ外使用正常的滑模变结构控制，在边界层φ内使用连续状态反馈控制，经过光滑处理的多约束螺旋机动变结构制导律为

(17)

(18)

(19)

2.4 机动策略设计与分析

为使滑翔飞行器在能有效躲过敌方拦截系统拦截的同时，还能满足制导精度和终端多种约束的要求，不能一味地追求单方面的性能，而需要将机动突防性能与制导精度进行综合考虑。由式(17)和式(18)可知，通过合理设计cdn和ctn的取值，可实现不同的机动策略。首先进行定性分析，可认为cdn和ctn的值越大，机动的幅值也越大；cdn和ctn取0时，制导律退化为不考虑机动的变结构制导。可制定如下三种制导策略：

(1)机动与制导串行策略

串行策略是传统的制导方案，即在俯冲前段只机动，不考虑制导精度和多约束限制；在俯冲后段不再机动，只进行多约束制导。该方案容易实现，但没有从俯冲全过程的视角出发，很可能导致设计的飞行轨迹不是最优的，甚至不能满足多约束限制。

(2)全程机动+制导的并行制导策略

在俯冲全段，保持cdn和ctn始终为较小的正值，保证飞行器在执行制导指令的同时，做机动飞行。该方案是一种理想的制导策略，但目前只依靠多约束螺旋机动变结构制导律这一种制导算法还不能保证足够的制导精度。

(3)先机动+制导、后制导的串并混合策略

结合前两种方案的优点，为提高高超声速飞行器俯冲段的精确打击和突防生存能力，制定以下串并混合策略：在俯冲初段，做大范围螺旋机动制导，尽快使拦截弹过载达到饱和临界状态；中段采用曲率半径较小的飞行迹线，位置变化进一步加快，拦截弹无法及时调整其自身制导律进行跟踪；飞行末段，不再机动，依靠多约束变结构制导方法集中机动能力，全力提高终端约束精度和制导精度。具体参数设置如表1所示。

表1 机动制导全程飞行策略

3 仿真分析

3.1 制导参数分析与优化

以美国CAV-H飞行器为仿真对象，验证所设计算法的有效性。采用目标(惯性)坐标系，目标固定在原点，取飞行器俯冲段起始位置坐标为(30 km，15 km，0)，速度v0=1700 m/s，弹道倾角θ0=0，弹道偏角φv=-180°。约束情况如下：攻角α∈[-25°，25°]，过载ny、nz∈[-15g，15g]，期望落角γdf=-90°，期望入射方位角γtf=130°；边界层厚度φ=0.001；机动参数cdn、ctn参照表1中机动制导策略进行选取，kdn=ktn=9，机动终止高度h=5 km。弹道解算步长为1 ms，制导指令更新周期为50 ms。

首先，分析趋近律系数k、切换项增益ε、角误差项系数λ三参数的不同取值对弹道特性的影响效果。其中，λ=10，ε=1.13，k=0.16为用于对比的标准值。结果如图1～图3、表2所示。

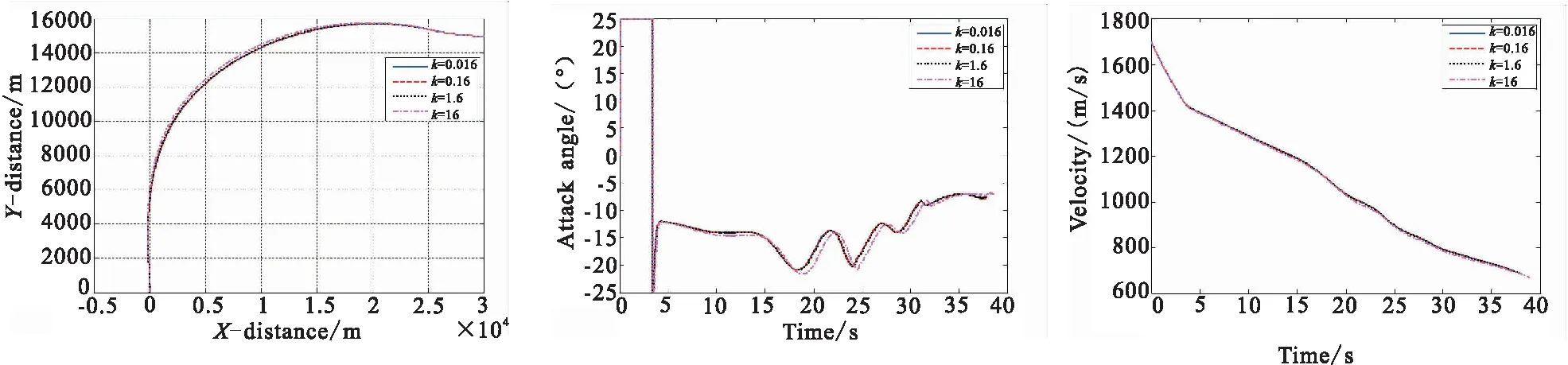
(a) Trajectory in the subduction plane (b) Attack angle curve (c) Velocity curve

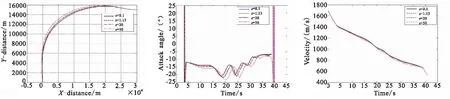
(a) Trajectory in the subduction plane (b) Attack angle curve (c) Velocity curve

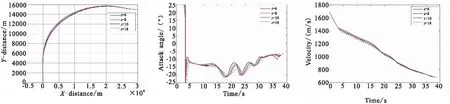
(a) Trajectory in the subduction plane (b) Attack angle curve (c) Velocity curve

表2 k、ε、λ值对弹道终端特性的影响

由图1和表2可知，k值在16以下时，飞行轨迹基本重合，k值对弹道特性没有显著作用。偏大或偏小的k值都会造成脱靶量和终端角度误差的增大。随着k值的增大，终端速度消耗量增多，终端速度下降速度变快；由图2和表2可知，ε值在20以下时，飞行轨迹基本重合，ε值对弹道特性没有显著作用。但ε值过大会导致弹道陡峭，攻角抖动加剧，易饱和；由图3和表2可知，偏大或偏小的λ值都会造成脱靶量和终端角度误差的增大。λ值越大，弹道越陡峭，弹道初始段被抬高的幅度越大，攻角变化越剧烈且易饱和。综上所述，在3个参数中，趋近律系数λ对弹道特性的影响相对而言是最强烈的。在对角误差项系数、趋近律系数、切换项增益的定性分析中，发现制导参数对制导性能的影响不是简单的线性关系，为达到最佳制导性能(脱靶量小，终端角度误差小)，需要给出合适的组合参数集。

因此，考虑对组合参数集进行优化，选取脱靶量,落角误差，入射方位角误差的平方和作为制导性能指标，用差分进化算法进行寻优。种群通过复制、交叉、变异等操作一代代不断进化，最终获得“最适应环境”的个体。一组较为优化的组合参数集为λ=10，ε=1.13，k=0.16。此时，脱靶量为1.06 m，落角误差为0.364°，入射方位角误差为0.908°，飞行时间为38.14 s。仿真结果如图4～图7所示。

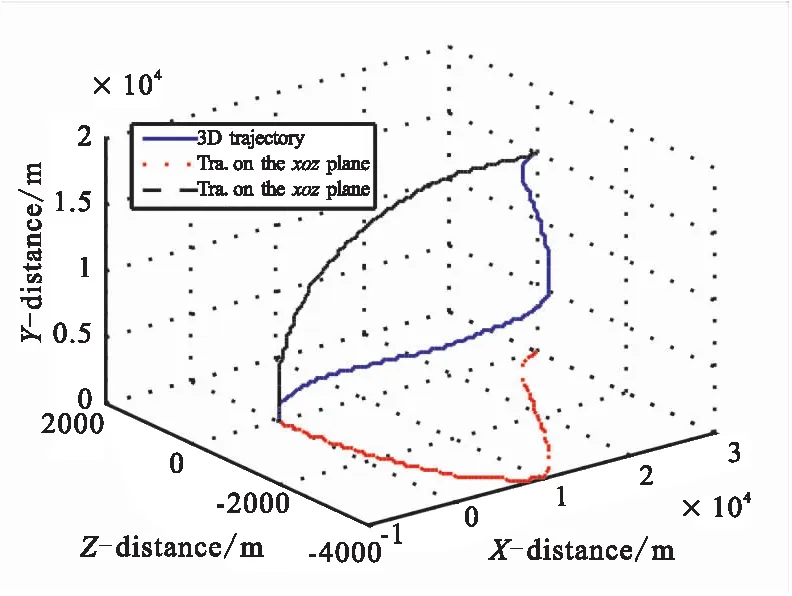
图4 飞行器的空间机动制导飞行轨迹图

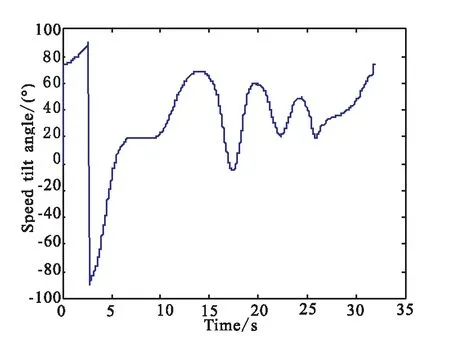
图5 速度倾侧角随时间变化曲线

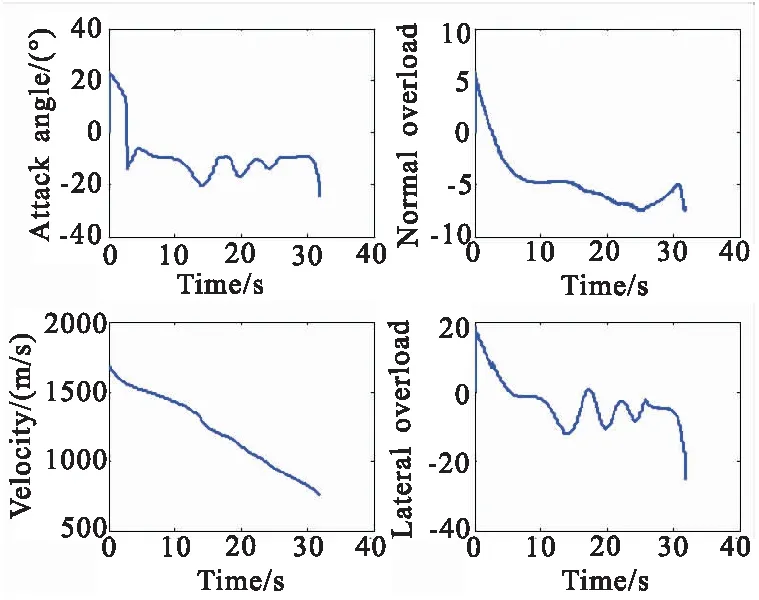
图6 速度倾侧角随时间变化曲线

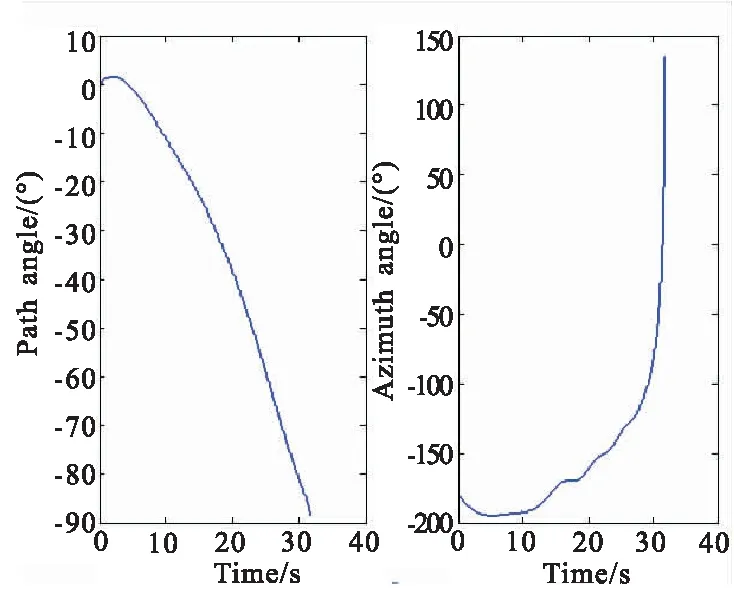
图7 速度方向角曲线

在俯冲初始段，飞行器做横向大机动，以调整航向，同时以较高的速率增大攻角的绝对值，为之后实现快速下压做准备。俯冲中段，飞行器在导向目标的同时做螺旋机动，转弯平面内以100 m左右的机动幅值进行机动；由机动运动控制项可知，机动运动控制量与飞行高度呈正弦函数关系，由于飞行高度呈非线性下降，因此过载的变化曲线没有周期性；为实现快速下压，攻角长期为负且较大。当飞行高度低于5 km时，飞行器转入全制导模式，不再机动，以确保有足够的制导精度，保证终端角度误差小，终端速度在[600 m/s,800 m/s]的范围内。综上分析，该制导律的制导精度较高，且能满足多种约束限制。

改变初始飞行条件，从不同的方位发射滑翔飞行器。初始条件为[路线1，路线2，路线3]={起始位置[(30 km，15 km，30 km), (-30 km，15 km，30 km), (30 km，15 km，-30 km)]，速度v0=[1700 m/s, 1700 m/s, 1700 m/s]，弹道倾角[θ0=0,θ0=0,θ0=0]，弹道偏角[ψv=-180°,ψv=0°,ψv=-180°]}。飞行轨迹如图8所示，终端参数如表3所示。仿真结果表明，螺旋机动变结构制导律可实现从各种方位开始俯冲机动飞行，对目标实现精确打击。

表3 多线路终端误差分析

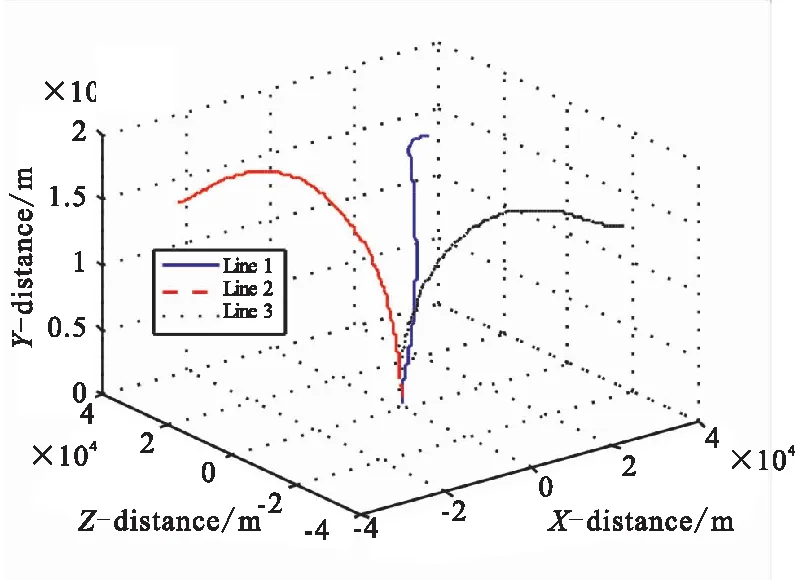
图8 多线路飞行轨迹仿真

3.2 蒙特卡洛仿真校验

通过Monte Carlo打靶仿真实验，可验证制导律在扰动条件下的鲁棒性。引入气动系数Cy、Cx及大气密度ρ偏差，均服从3σ=15%的高斯分布，进行500次模拟打靶。仿真结果如图9、图10和表4所示。结果显示，落点的50%圆概率偏差为1.225 0 m，落角偏差小于2°，入射方位角偏差小于1.5° 。制导精度较高，算法鲁棒性较好。

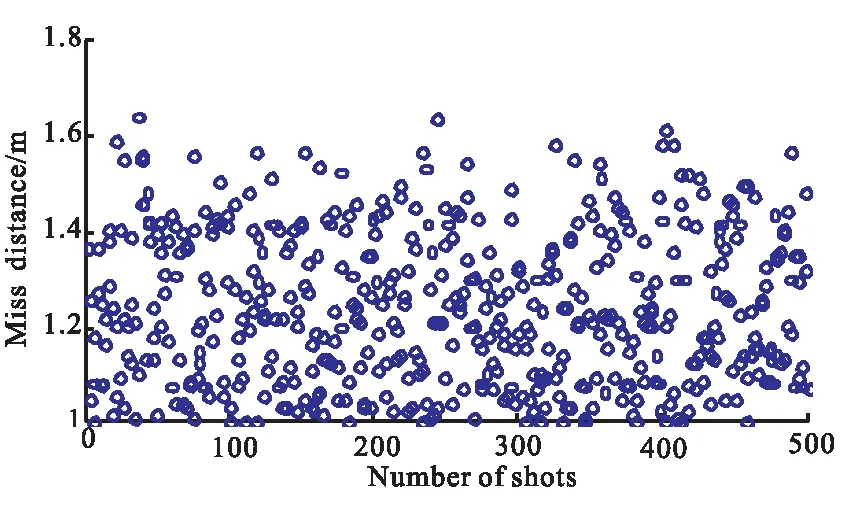
图9 模拟打靶落点分布

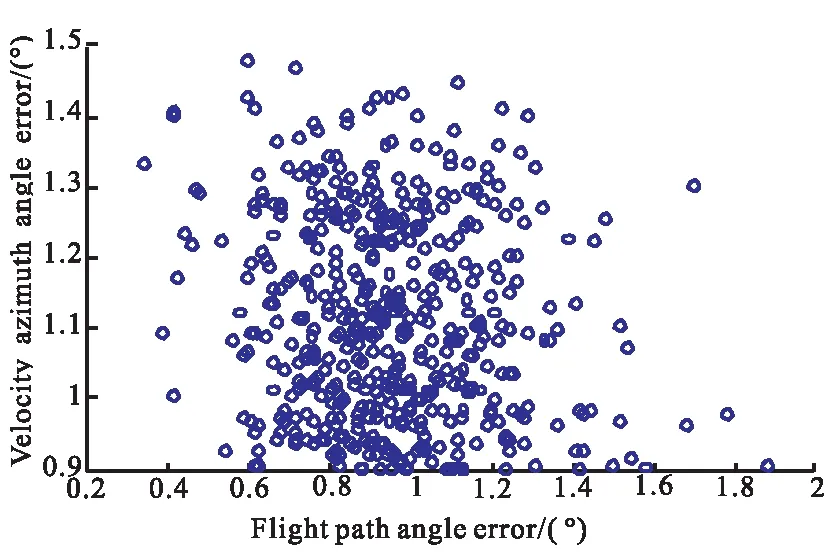
图10 模拟打靶终端角度分布

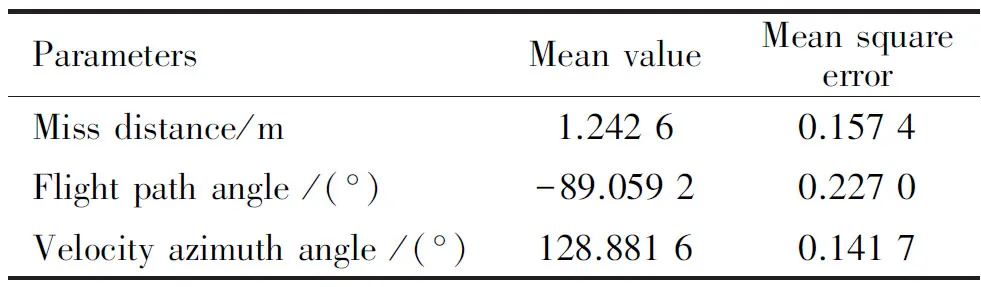
表4 约束统计量特性分析

3.3 机动制导策略分析对比

将本文提出的串并混合制导策略与传统串行机动制导策略进行对比。两种策略下的过载控制量变化情况如图11所示。与采用的串并混合方案相比，传统方案不易确定制导律的切换时机，切换时过载会出现激增现象，且末段过载易饱和，制导效果相对较差。

3.4 机动突防能力分析

用PAC-3反导导弹作为拦截弹，进行攻防对抗仿真。假定PAC-3弹上装载的制导算法为三维变结构制导律，采用STT控制方式。约束情况如下：攻角α∈ [-25°，25°]，过载ny、nz∈[-20g，20g]。当CAV-H飞行器从初始位置开始俯冲时，同一时间，目标所在位置坐标(0，0，0)处发射一枚PAC-3导弹，对飞行器进行拦截。攻防对抗仿真结果如图12和图13所示。

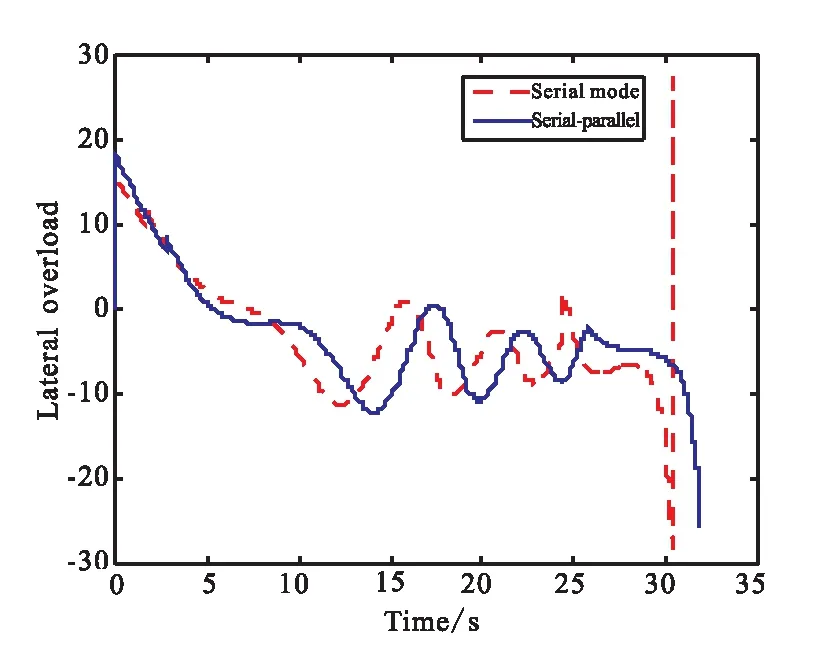
图11 两种机动制导全程过载对比

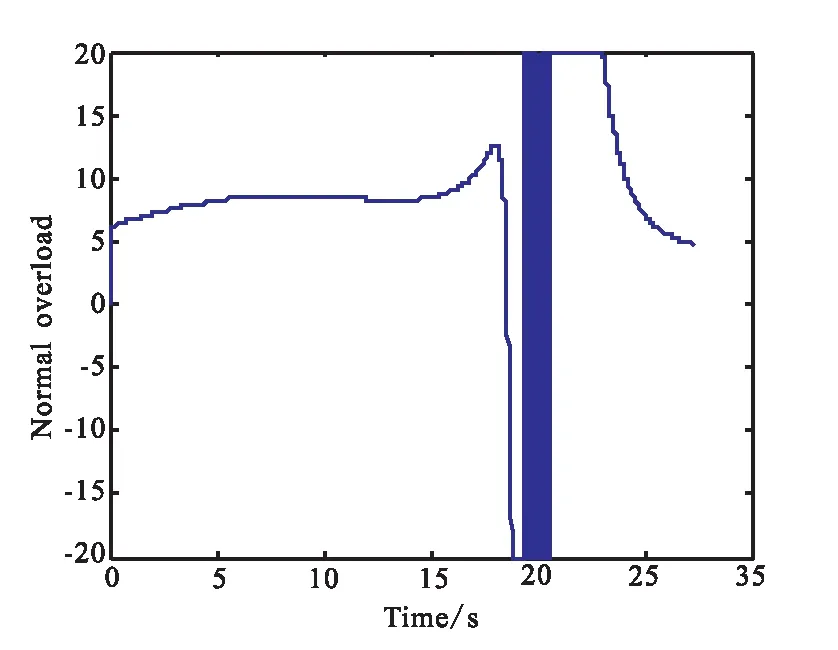
图12 拦截弹法向过载随时间的变化曲线

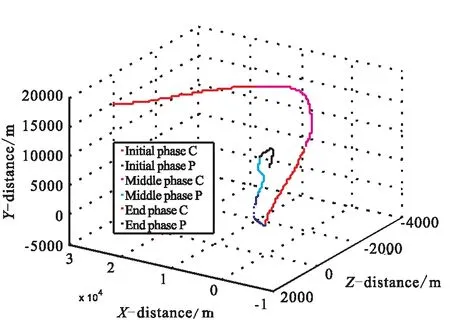
图13 防对抗仿真轨迹

仿真结果显示，在机动情况下，拦截弹的脱靶量为3244.7 m，在滑翔飞行器俯冲初段和中段的机动干扰下，该拦截弹的需用过载超出PAC-3导弹的自身可用过载限制，造成脱靶拦截失败。初段大范围的螺旋机动造成拦截弹需用过载的不断增大，当转入中段机动制导不久，拦截弹需用过载迅速饱和。该仿真分析初步说明了采用多约束螺旋机动变结构制导律进行机动突防是一种有效的突防手段。

4 结论

(1)本文针对BBT控制方式的高超声速滑翔飞行器，通过对在双平面解耦下的相对运动系统进行滑模变结构控制，设计了一种考虑多种约束限制的螺旋机动变结构制导律和制导策略。仿真结果表明，该方法能够满足俯冲段终端落点和角度约束，精度较高，鲁棒性较好；同时，可实现预期的螺旋机动飞行，提高了飞行器机动突防和生存能力。

(2)本文未能涉及BTT控制的情况，因其会带来通道严重耦合，故在下一步的研究中，需要设计非解耦情况下的俯冲攻击三维制导律。