平面滑动闸门在不同结构体系下的静力计算分析方法

付鹏鹏，徐慧宁，殷国富*,，杨汉骞，杨传玉

平面滑动闸门在不同结构体系下的静力计算分析方法

付鹏鹏1，徐慧宁1，殷国富*,1，杨汉骞2，杨传玉2

（1.四川大学 机械工程学院，四川 成都 610065；2.四川省水利水电勘测设计研究院，四川 成都 610072）

传统的闸门设计基于平面结构体系，通过简化受力模型对各个构件进行计算，并未考虑构件间的变形协调关系；实际的闸门为空间结构体系，各个几何构件之间相互协调，受力更加复杂。通过对平面体系和空间体系计算原理的分析论述，建立了一种平面滑动闸门在不同结构体系下的静力计算分析模型，通过典型工程实例，基于平面体系计算方法和空间体系计算方法对闸门强度、刚度进行校核计算。结果显示，两种结构体系下，主梁前翼缘正应力和面板折算应力误差较大。最后通过假设，并利用对假设进行验证表明：平面体系计算中，由于主梁的应力计算没有考虑水平次梁的参与，导致主梁前翼缘正应力误差较大，进而引起面板折算应力误差较大。同时，对于其它构件误差也进行了误差分析，提出了一定的要求，为设计人员设计类似闸门和改进平面计算方法提供了参考。

平面结构体系；空间结构体系；有限元；校核计算；误差分析

目前，闸门的设计计算主要基于平面体系。平面体系计算方法是将构件逐个独立地进行计算，计算模型简单方便，因而得到广泛应用。但其没有考虑各构件间的整体工作协调性，不能准确反映整个闸门各构件间的相互作用及变形协调，结果不是很准确[1-4]。闸门实际为空间结构，计算复杂，要对闸门进行建模、单元离散及计算分析，对计算机软硬件要求较高，其计算结果更真实、准确。目前虽然闸门结构空间有限元法分析的文章很多，但主要还是利用空间体系算法对闸门结构进行校核计算。纪伟等[5-6]虽有使用两种体系计算法对闸门校核计算，但没有对两种计算结果更深入的分析。鉴于闸门设计计算仍然以平面体系计算为主，为了比较两种体系计算结果的差异性，本文通过实例，运用ANSYS软件对某导流洞封堵门进行空间体系计算，与平面体系计算结果进行对照和分析。为类似闸门的设计及平面体系计算方法的改进提供了参考。

1 使用平面滑动闸门的工程背景

某大型水库导流洞布置在左岸，共1孔，进口段设导流洞封堵门1扇，用于导流洞堵头施工期挡水。闸门采用潜孔平面滑动门，门叶面板及水封均布置于下游侧，门叶结构主要材料为Q345B，主支承采用高强度复合材料滑道。门叶分3节制造和运输，工地焊接拼装。参数如表1所示，孔口型式为潜孔式；操作条件为小于设计闭门水头动水闭门，小于设计启门水头动水提门；启闭机采用单吊点2000 kN固定卷扬式启闭机。

表1 导流洞封堵门闸门参数

2 计算原理与分析模型

2.1 平面体系计算原理

目前，闸门结构力学计算模型主要采用平面体系，未考虑重力影响，把一个空间承重结构划分成几个独立的平面系统，即把平面闸门分为面板、水平次梁、竖直次梁、主梁、边梁、支承等构件。闸门所承受的水压力近似按图1所示顺序传递，然后依次对各个构件进行分析计算，受力模型如图2所示[7]。

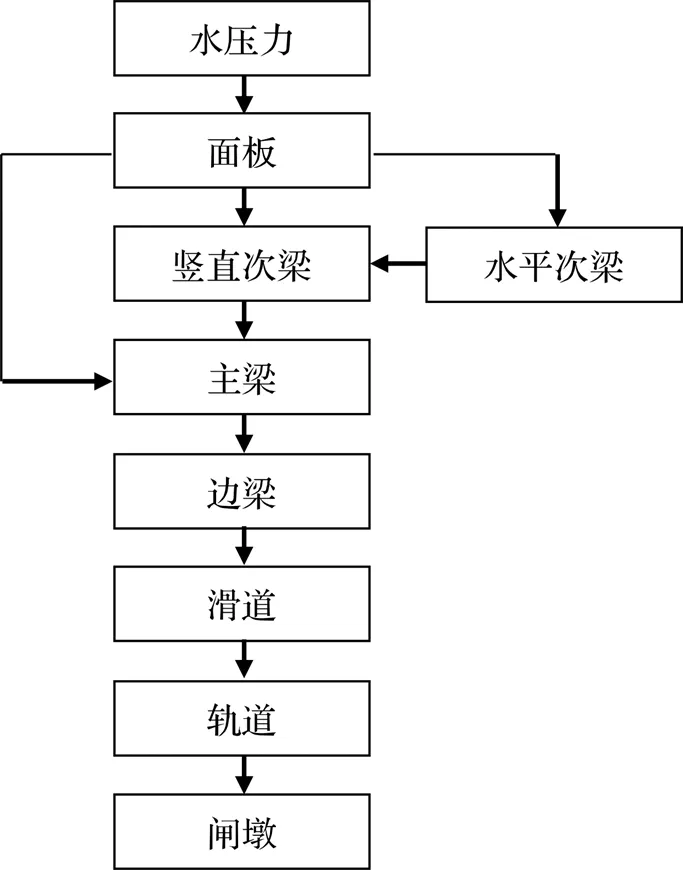
图1 闸门水压力传递途径

面板属于典型的薄板结构，根据弹性薄板理论，按照四边固定、三边固定一简支和两边固定两边简支计算局部弯应力，同时还要考虑主梁整体弯曲对面板的影响，故面板计算时，必须将面板的局部弯应力和主梁的整体弯应力相叠加，验算其折算应力[8]。

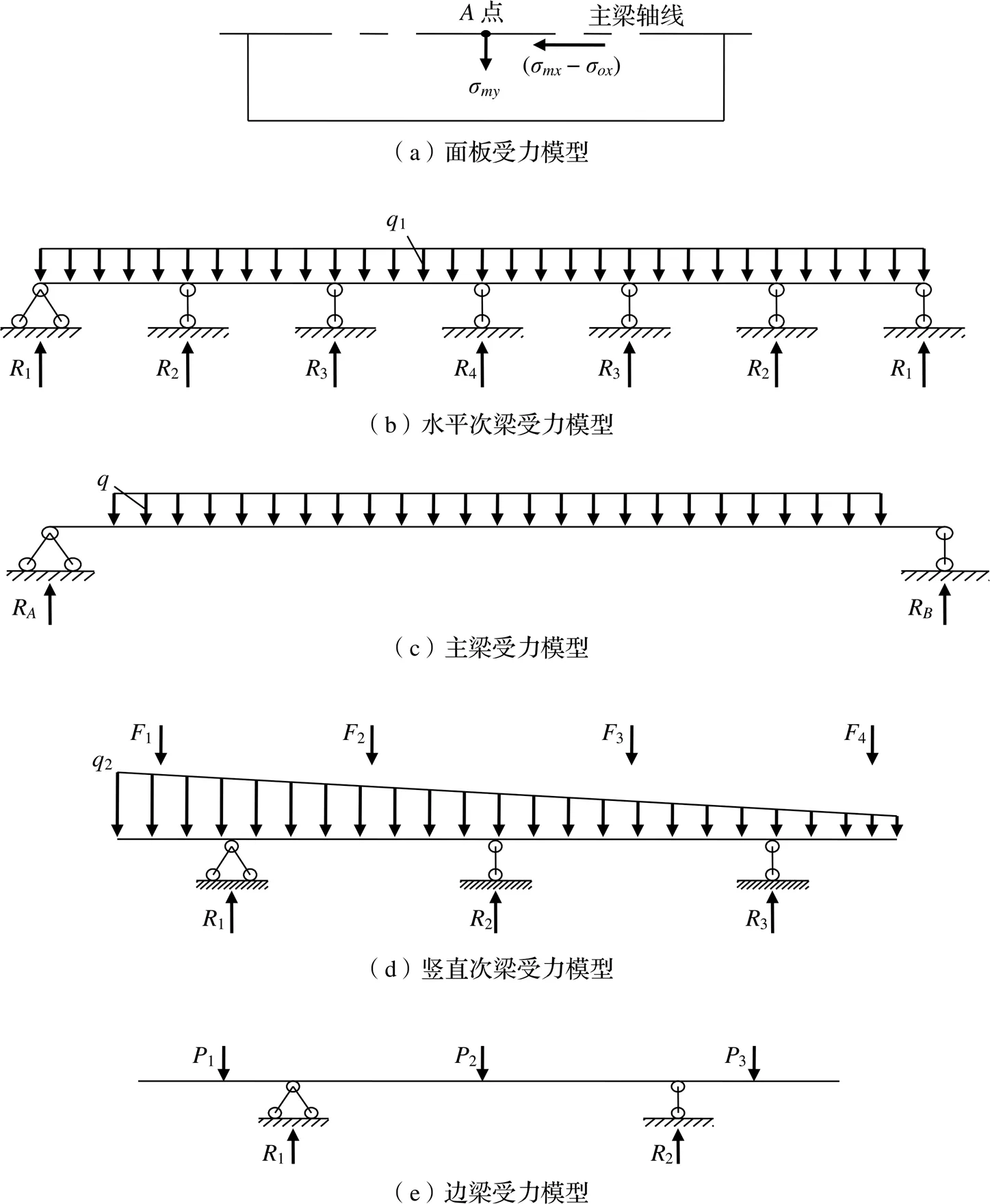
图2 构件受力模型

水平次梁支承在竖直次梁上，承受面板传来的部分水压力，按照等分法以线荷载的形式将水压力分配给各水平次梁，此时水平次梁可简化为承受均布荷载的多跨连续梁进行计算。

竖直次梁支承在主梁上，承受水平次梁传递过来的集中力以及按等分法所分配的三角形或梯形水压荷载，按照带悬臂段的简支梁进行计算。

主梁支承在边梁上，承受梁格传递的总水压力，根据力矩法将面板上水压力以主梁所在位置划分成若干个小梯形水压力，然后求出各个小梯形水压力合力并作用在对应的简支梁上，则支座反力便是该主梁上的荷载。最后，对主梁按照承受均布荷载的简支梁进行计算。

边梁通过滑道支承在闸墩上（简化为点支承），承受主梁传递的集中荷载，按照承受集中力的带悬臂段的简支梁进行计算。

2.2 空间体系计算原理

闸门是一种典型的空间薄壁结构体系，由一系列板、壳、梁等构件组成，如图3所示。根据闸门结构形式和受力特点，将闸门面板、主梁、水平次梁、竖直次梁、边梁离散为shell181单元，滑道离散为solid185单元[9]。据此基于ANSYS软件所建立的闸门有限元计算模型如图4所示，计算模型的节点总数为184578个，单元总数为188439个。

闸门结构材料为Q345B，其弹性模量＝2.06×105N/mm²，泊松比＝0.3，密度＝7850 kg/m3，重力加速度取9.8 m/s²，方向竖直向下。根据工程经验，面板考虑1 mm的腐蚀裕度，焊缝重量约为闸门重量的3%，建模中未予以考虑，故对钢材密度进行修正：

＝7850×1.03＝8085 kg/m3

图3 闸门结构几何模型

图4 闸门有限元模型

计算工况及约束条件：闸门处于全关位置，面板及止水位于下游侧，受到上游侧85 m水头的静水压力。为边梁底部竖直方向的位移约束；为滑道外表面法线方向的位移；为面板中线垂直水流方向的水平位移。

3 强度、刚度评判标准

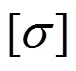
[]＝135×0.9＝121.5 MPa

导流洞封堵门属于潜孔式工作闸门，计算跨度为8.04 m，根据文献[8]，其主梁最大挠度与计算跨度之比不应超过1/750，即最大允许挠度为10.72 mm。

4 计算结果与分析

最高水头下闸门应力和变形分布如图5。

水压力及闸门自重作用下，闸门结构应力分布复杂。按照第四强度理论对闸门进行强度校核计算，第四强度校核公式为：

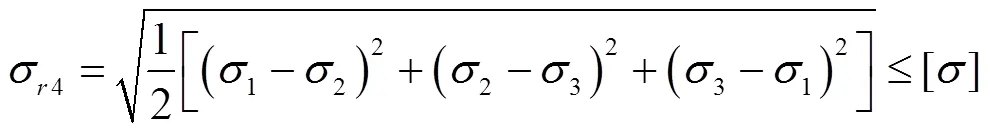
验算面板强度时，应考虑面板的局部弯应力与面板兼作主（次）梁翼缘的整体弯应力叠加。由于本闸门所有面板区格长宽之比/＞1.5，平面体系计算只需要验算区格沿主梁轴线长边中点的折算应力：

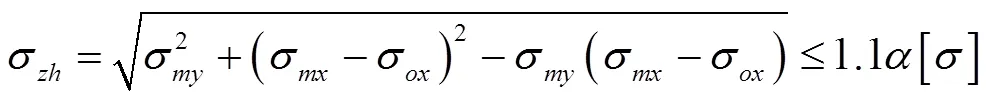
4.1 主梁最大应力

表2为闸门最高挡水位下，平面体系和空间体系下主梁最大应力和挠度计算结果对照，可知，除主梁前翼缘正应力外，两种体系计算结果基本一致，误差均在5%以内，且均小于容许值。

平面体系计算未考虑构件自身重力的影响，水压力根据力矩重心法近似分配，并假设作为支承的边梁为绝对刚性，没有位移。同时，对于参与主梁计算的面板宽度也是近似考虑，因此结果会有所差异。

图5 最高水头下闸门应力、变形分布图

表2 主梁最大应力和挠度

主梁前翼缘应力产生较大误差的原因是：平面体系主梁计算偏安全，并未考虑水平次梁的参与，而水平次梁位于面板侧，由此假设引起计算误差较大的原因是水平次梁的影响。现在平面体系计算中考虑水平次梁影响，近似将水平次梁截面积折算到面板中，对于主梁前翼缘再次进行计算，其值为109.1 MPa，109.1/115.3＝0.946，误差降为5.4%，假设正确。

4.2 面板折算应力

如图6所示，空间体系面板最大折算应力σ＝145.5 MPa，平面体系σ1＝223.5 MPa，两种结果均小于容许应力，但223.5/145.5＝1.536，误差较大。

图6 面板空间体系折算应力分布（MPa）

面板折算应力产生较大误差的原因是：根据弹性薄板理论，面板最大折算应力出现在以主梁为区格长边的中点位置，通过查询系数近似计算，对结果有一定影响，但不是主要原因。根据主梁计算结果分析，主梁前翼缘正应力误差较大，其将直接影响面板折算应力，其误差会直接传递给面板折算应力的计算。在平面体系计算中，将式（2）中σ1值变更为考虑水平次梁后的值σ2再次进行计算，此时，面板最大折算应力σ2＝162.8 MPa，σ2/σ＝1.119，误差降为11.9%，可见水平次梁会间接影响主梁前翼缘处面板折算应力的计算结果。

4.3 边梁最大折算应力

如图7所示，在与主梁连接处折算应力较大，最大折算应力为109 MPa，而平面体系结果为95.5 MPa，平面体系计算结果小于空间体系计算结果，两者均小于容许应力。

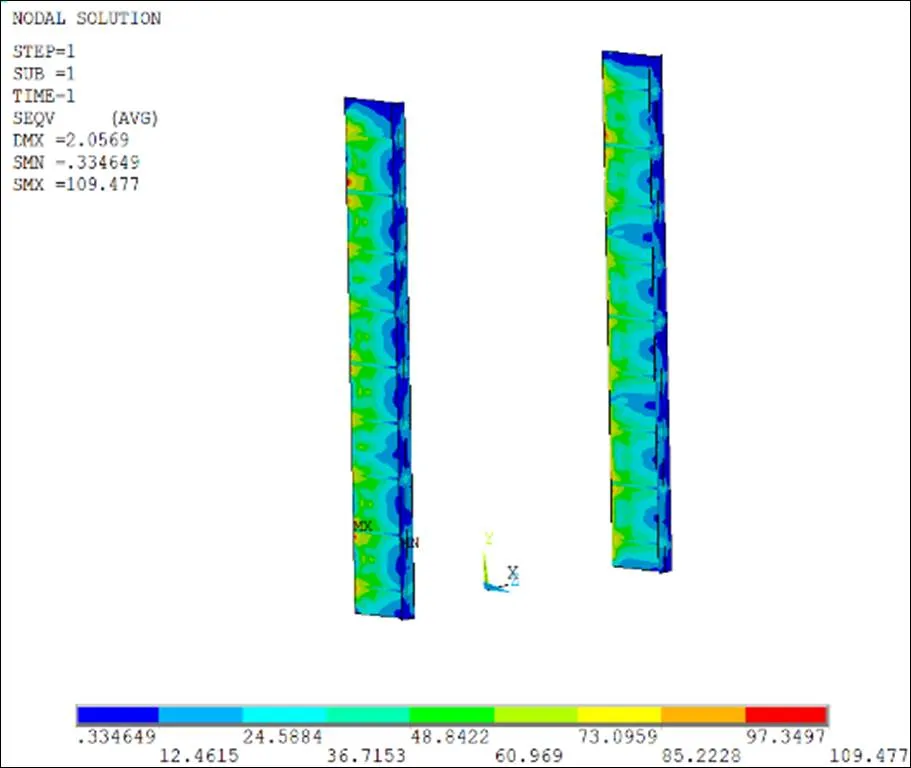
图7 边梁空间体系折算应力分布（MPa）

边梁折算应力误差产生的原因是：平面体系计算中，边梁受力模型简化为点支承，仅承受主梁集中荷载，未考虑自身重力及变形协调作用，为二向应力状态。实际的边梁支承型式为滑道支承，属于线面支承，承受主梁、水平次梁、面板传递过来的力和自重，在主梁和水平次梁交接处为三向应力状态，受力较为复杂，应力较大。因此，平面体系计算中边梁计算要适当考虑安全裕度，保守计算。

4.4 水平次梁最大折算应力

如图8所示，最大折算应力为123.7 MPa，而平面体系为134.4 MPa，两种计算结果均小于容许应力，134.4/123.7＝1.086，误差为8.6%。

水平次梁折算应力误差产生的原因是：平面体系计算中，未考虑水平次梁自重影响，面板参与计算宽度也为近似取值，并且水平次梁支承在竖直次梁上，为弹性支承，而平面计算中考虑为刚性支承，没有位移，计算结果会有所差异，但误差不大。

图8 水平次梁空间体系折算应力分布（MPa）

4.5 竖直次梁最大折算应力

如图9所示，在主梁后翼缘及水平次梁相交处应力较大，最大折算应力为148.9 MPa，而平面体系为95.2 MPa，两种计算结果均小于容许应力。

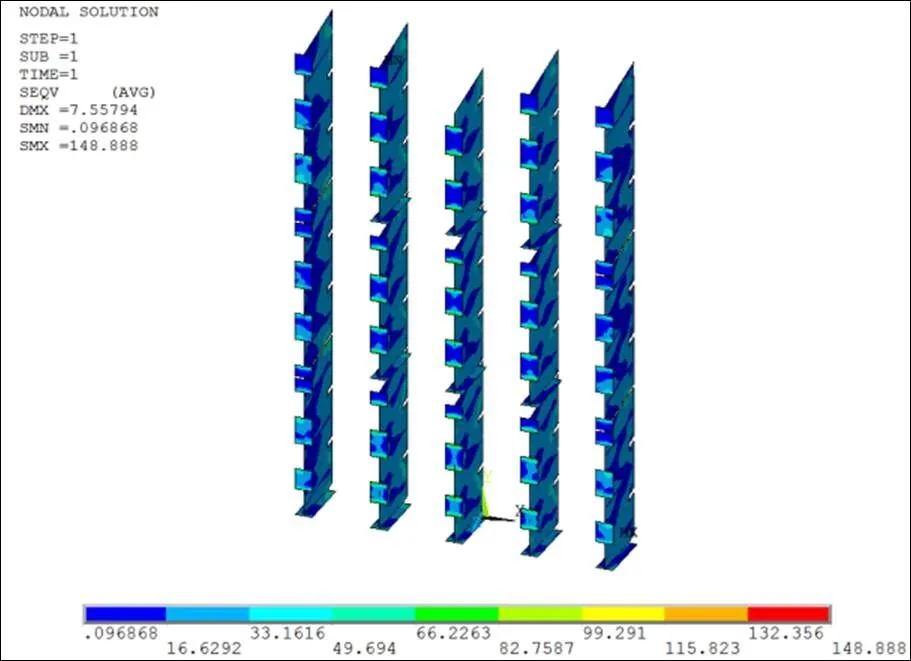
图9 竖直次梁空间体系折算应力分布（MPa）

竖直次梁折算应力误差产生的原因是：平面体系计算中，未考虑竖直次梁自重影响，面板参与计算宽度也为近似取值，并且竖直次梁支承在主梁上，为弹性支承，而平面计算中考虑为刚性支承，没有位移，计算结果会有所差异。同时，在竖直次梁在与主梁相交处，不仅要承受自身的弯应力和剪应力，还要承受主梁后翼缘应力影响，属于三向应力状态，受力复杂，折算应力较大，而平面体系中计算考虑为二向应力状态。因此，平面体系计算中竖直次梁计算要适当考虑安全裕度，保守计算。

5 结语

（1）通过工程实例，运用平面体系法和空间体系法进行校核计算，结果表明，闸门结构强度和刚度均满足设计要求。

（2）由于自重相对于水压力对构件强度计算影响较小，所有构件的平面体系计算均未考虑自重的影响。

（3）主梁支承考虑为刚性支承，实际支承在边梁上，支座为弹性支承，同时面板参与计算宽度为近似取值，对主梁的计算结果有一定影响。主梁的计算由于未考虑水平次梁的参与，导致主梁前翼缘正应力偏大，进而引起面板折算应力偏大，对于类似闸门应将水平次梁的影响考虑进去。

（4）边梁实际受力较为复杂，计算模型简化较多，与实际模型计算结果差别较大，在主梁和水平次梁相交处为三向应力状态，平面体系计算值小于空间体系真实值，设计人员应当对边梁进行保守设计，保证边梁强度满足要求。

（5）水平次梁支座考虑为刚性支承，实际支承在竖直次梁上，支座为弹性支承，同时面板参与计算宽度为近似值，均会引起计算值和实际值的误差。

（6）竖直次梁支座考虑为刚性支承，实际支承在主梁上，支座为弹性支承，在与主梁和水平次梁相交处为三向应力状态，受主梁和水平次梁翼缘影响较大。因此竖直次梁要进行保守计算，保证满足强度要求。

（7）本文对照和分析了平面滑动闸门平面体系和空间体系计算真实结果的异同，为改进类似闸门的平面体系设计计算方法提供了参考。

[1]孙琳. 平面定轮闸门三维有限元分析[J]. 水利规划与设计， 2013，（5）：37-40.

[2]王好强. 平面钢闸门静动力分析与优化设计[D]. 南京：河海大学，2006.

[3]王正中，张雪才，刘计良. 大型水工钢闸门的研究进展及发展趋势[J]. 水力发电学报，2017，36（10）：1-18.

[4]叶永丰，杨光明. 后止水平面钢闸门结构加固有限元分析[J].人民黄河，2015，37（7）：110-112，116.

[5]纪伟，任玉珊. 基于有限元法的平面钢闸门结构整体性优化设计[J]. 人民珠江，2015，36（3）：76-81.

[6]周旭云. 深孔闸门受力分析方法探讨[D]. 南京：河海大学， 2005.

[7]刘细龙，陈福荣. 闸门与启闭设备[M]. 北京：中国水利水电出版社，2002.

[8]SL 74－2013，水利水电工程钢闸门设计规范[S]. 北京：中国水利水电出版社，2013.

[9]王新敏，李义强，徐宏伟. ANSYS结构分析单元与应用[M]. 北京：人民交通出版社，2011.

Static Calculation Analysis Method of Plane Sliding Gate under Different Structure Systems

FU Pengpeng1，XU Huining1，YIN Guofu1，YANG Hanqian2，YANG Chuanyu2

( 1.School of Mechanical Engineering, Sichuan University, Chengdu 610065, China; 2.Sichuan Water Resource and Hydroelectric Investigation and Design Institute, Chengdu 610072, China)

Traditional gate design is based on plane structure system, and the calculation of each component is carried out by simplifying the mechanical model, without taking the deformation coordination relationship among the components into consideration. While the gate in actual use is a spatial structure system, of which the components coordinate with each other, and the stress is far more complex. On the basis of the analysis of the calculation principles of both plane system and spatial system, a static calculation and analysis model of plane sliding gate under different structural systems is established. And through typical engineering cases, the check calculation of the gate strength and stiffness is carried out based on the calculation method of plane system and spatial system. The result shows that the error between the normal stress of the main beam front flange and the equivalent stress of the panel under the two structure systems. Finally, the errors is verified by hypothesis. It turns out that in the calculation of plane system, the normal stress error of main beam front flange is large because the secondary horizontal beams is not taken into consideration in the stress calculation of main beam, which leads to a large equivalent stress error of the panel. At the same time, the error analysis of other components is also carried out, and certain requirements are put forward, which provides reference for the design of similar gates and the improvement of the plane calculation method.

plane structure system；spatial structure system；finite element；check calculation；error analysis

TV663+.4

A

10.3969/j.issn.1006-0316.2020.07.005

1006－0316 (2020) 07－0028－07

2020－02－18

2017年四川省中国制造2025四川行动资金项目（2017MY00355）

付鹏鹏（1989–），男，河南沁阳人，硕士研究生，主要研究方向为数字化设计及水工金属结构。

殷国富（1956－），男，四川西充人，教授、博士生导师，主要研究方向为产品数字化设计、制造自动化、CAD/CAPP/CAM等，E-mail：gfyin@scu.edu.cn。