高速超声振动切削的最佳主偏角适用范围

徐继业，涂军，余德平

高速超声振动切削的最佳主偏角适用范围

徐继业，涂军，余德平*

（四川大学 机械工程学院，四川 成都 610065）

为了研究高速超声振动切削过程中主偏角对切削力的影响，建立了高速超声振动切削的理论模型。首先分析了高速超声振动切削在不同主偏角下的切削力分布，然后计算了不同切削区域的切削厚度和单位切削宽度，以及四个金属切削变形区的切削力，最终建立了高速超声振动切削在0～90°主偏角下的切削力模型。理论和实验结果表明，对于主切削力而言，主偏角变化范围为20°～55°时，高速超声振动切削主切削力小于常规切削主切削力；对于进给抗力而言，主偏角适用范围为15°～40°；对于吃刀抗力而言，主偏角适用范围为15°～45°。为了使高速超声振动切削的切削效果达到最好，最佳主偏角适用范围为20°～40°。

高速超声振动；主偏角；切削力；直线切削刃；微加工

超声振动切削是一种精密加工方法。隈部淳一郎[1]于20世纪70年代提出一维超声振动切削技术，采用这种切削技术能够有效降低切削力，改善工件表面加工质量，实现工件的精密加工。椭圆超声振动切削在20世纪90年代由SHAMOTO[2]提出，这种加工方法具有减小切削力和改善工件表面质量的效果。MA等[3]研究表明，椭圆超声振动切削能够有效提高加工精度。XIAO等[4]研究发现椭圆超声振动切削还可以抑制再生颤振，实现毛刺高度的降低和刀具寿命的延长。

王致坚等[5]研究了振动切削在螺纹加工中的应用，研究表明振动攻丝的切削力呈现出明显的波形，攻丝扭矩的均值低于普通攻丝。BREHL等[6]提出了超声振动切削临界切削速度的概念，研究发现，一维超声振动切削和椭圆超声振动切削的优点都是在切削速度小于临界切削速度下才能体现出来，而临界切削速度远小于常规切削的切削速度，并且随着切削速度的增加，切削效果逐渐减弱，最终和常规切削效果一样。因此，由于受临界切削速度的限制，一维超声振动切削和椭圆超声振动切削都只适用于低速加工领域，而不能应用于高速加工领域。北航张德远教授等[7]提出了高速超声振动切削（HUVC，High-speed Ultrasonic Vibration Cutting）。对于一维超声振动切削和椭圆超声振动切削，刀具沿着切削速度或垂直于进给方向振动，而HUVC刀具沿着进给方向振动，从而可以突破切削速度的限制实现高速切削，应用于高速加工领域。HUVC具有减小切削力、改善工件表面质量、提高加工精度、延长刀具使用寿命等优点。

常规切削的力学建模方面，DORLIN等[8]研究了刀尖圆弧半径和切削刃圆弧半径对切削力的影响，研究表明切削刃圆弧半径和后刀面磨损对切削力的影响较大。CRICHIGNO等[9]建立了主切削力和背向力的切削力模型，研究了切削温度对切削力的影响。JEONG等[10]建立了传统切削切削刃为圆弧形的力学模型，并考虑了负前角和后刀面摩擦系数对切削力的影响。在超声振动切削的力学建模方面，BAI等[11]建立了椭圆超声振动切削的正交切削模型，研究表明瞬态剪切角的变化受刀屑摩擦角的影响。NATEGE等[12]建立了超声振动切削的静力学和动力学模型，并研究了切屑的流出方向对切削力的影响。综上，较少有人研究高速超声振动切削过程中主偏角对切削力的影响。

对比常规切削，在做不同切削变量和刀具几何参数对HUVC减小切削力效果的预实验过程中，发现不同主偏角下HUVC降低切削力的效果有较大的差异，其他因素诸如工件转速、刀具前角和后角等对HUVC降低切削力的效果影响很小。为了更好地研究切削过程中主偏角对HUVC切削力的影响，先建立HUVC在0～90°主偏角下的切削力模型；设计实验验证模型的有效性；计算相比常规切削，HUVC在不同主偏角下减小切削力的效果；综合理论和实验结果，分析HUVC的最佳主偏角适用范围。

1 HUVC在不同主偏角下的切削力模型

1.1 HUVC原理

根据张德远教授[7]提出的HUVC模型，建立如图1所示圆柱坐标系。

r为工件半径，mm；θ为工件旋转角度，°；z为工件进给方向；ap为切深，mm；n为工件转速，r/min；f为刀具进给速率；p(r, θ, z)为刀尖的位置

圆柱坐标系定义在旋转工件上，与传统超声振动切削的振动方向不同，HUVC沿着刀具进给方向振动，刀具轨迹沿进给方向呈螺旋线。

运动学模型可由描述为：

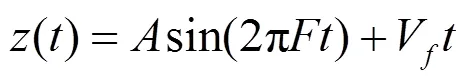
式中：V为工件进给速度，设置V＝0.01 mm/r；为工件直径，设置＝30 mm；为超声振子振动频率，设置＝19.97kHz；为超声振子振幅，设置＝20μm；设置＝800 r/min。

综合式（1）～式（3），在工件旋转的任意时刻，刀具运动轨迹可描述为：

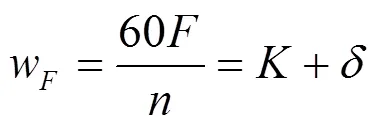
式中：代表工件旋转的圈数；为相邻切削轨迹的相位偏移，rad；W为超声振子振动频率对工件转速的比值；为比值的整数部分；为小数部分；为走刀时间，s。

受先前相邻刀具切削轨迹的影响，工件已加工表面轮廓可描述为：

式中：0为先前影响已加工表面形貌的切削轨迹数量，由进给速率和超声振子振幅决定。

HUVC能体现出降低切削力、改善工件表面质量和延长刀具使用寿命等效果，在于切削过程中刀具与工件的间断性分离。如图2所示，刀具在一个振动周期内，从1到2，刀具与工件接触，为切削阶段，从2到下一个周期开始刀具和工件分离，为分离阶段。

为保证切削过程中刀具和工件有间断性分离，实现高频断续切削，需满足以下两个条件：

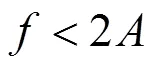
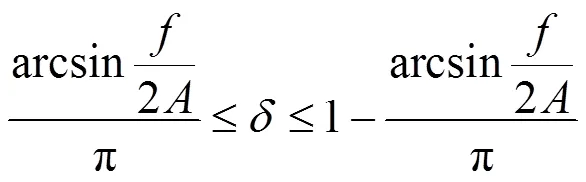
T为超声振子的振动周期

图2 HUVC切削分离图

1.2 HUVC在不同主偏角下的切削力分布

如图3所示，1为刀具主切削刃，在t时，刀具主切削刃由1运动到12，阴影部分为HUVC在一个振动切削周期内t时的切削区域。其中为切深k为直线主切削刃所对应的主偏角，为切削刃圆弧半径，h为刀具参考平面内t时所对应的长度。1～2为刀具与工件接触阶段，刀具处于切削状态，h可计算为：

为了描述切削区域的切削力沿着直线切削刃的分布情况，引出辅助角ε，辅助角从1到12变化，变化范围为0～π/2，h(ε)是辅助角为ε时的切削厚度，即12的长度，切削厚度可以由h、辅助角ε和切深计算出来。此外，图3给出了辅助角为ε时，12法向截面的前视图，在刀具参考平面内，切削厚度h(ε)与法向截面待切削的厚度相等。

1.3 HUVC切削区域的切削厚度和单位切削宽度

切削力沿着直线切削刃分布时，不同h(ε)对应的切削力大小不同，把切削区域随着辅助角ε的变化划分为若干个无限小的区域，分别计算每个微小区域内的切削力，再把所有微小区域内的切削力累加，得到整个切削区域对应的切削力，即为HUVC在一个振动周期内t时的瞬态切削力。

把在0～π/2变化的辅助角分为份时，切削区域被划分为若干个微小区域，当趋向于无穷大时，这些微小区域逐渐趋近为平行四边形，每个近似平行四边形微小区域面积计算方式是辅助角为ε时所对应的h(ε)乘以此辅助角下对应的单位切削宽度。

h(ε)的计算分为两种情况，如图4所示为临界情况，此时的辅助角为临界辅助角1，计算公式为：

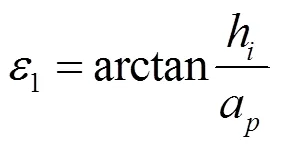
当辅助角分别在0～1、1～π/2变化时，对应的h(ε)如图5所示。

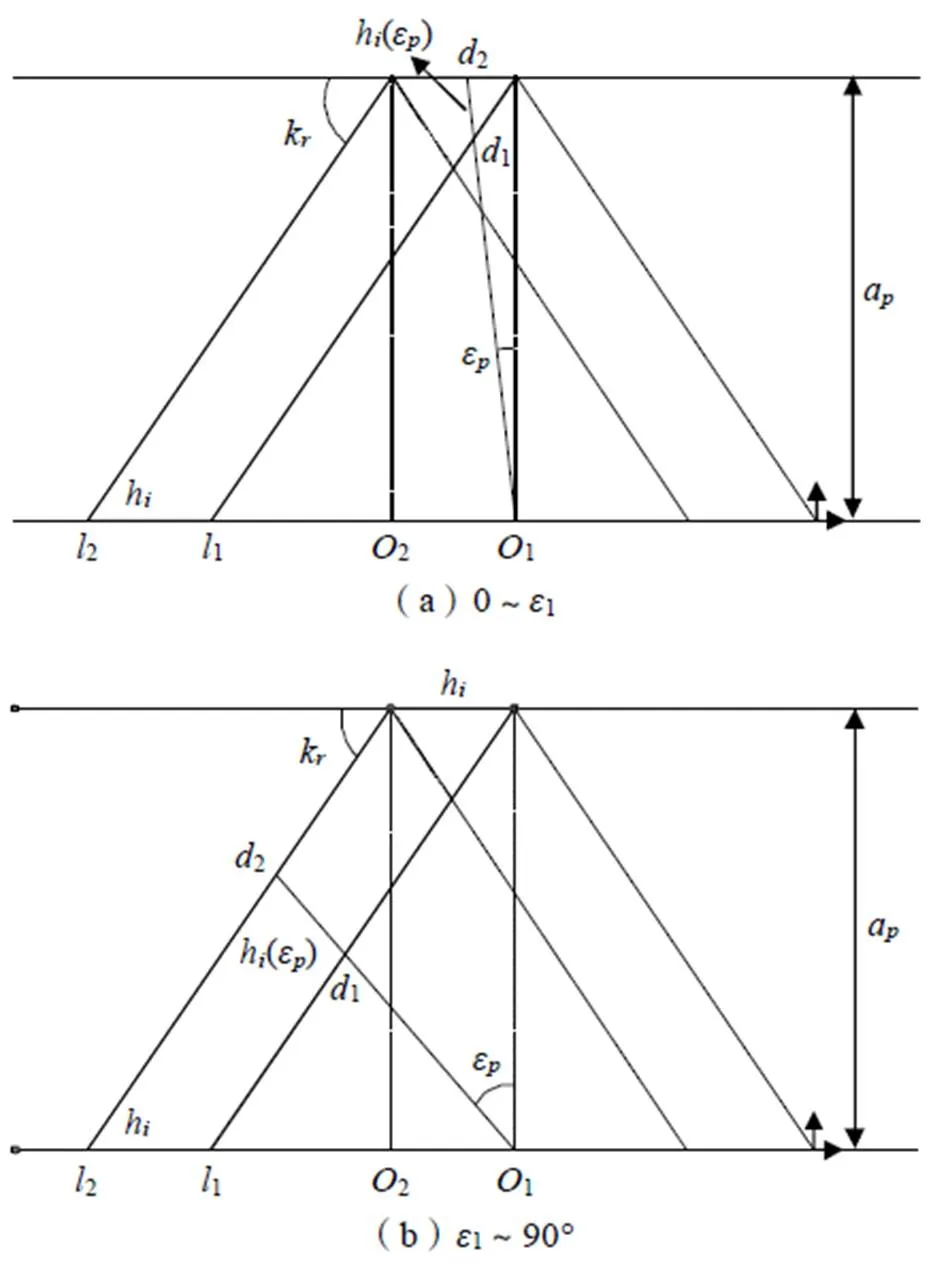
图5 不同辅助角下hi(εp)的计算示意图

综上，切削厚度计算为：

其中，把辅助角在0～π/2分为份时，有：

图6 不同辅助角下单位切削宽度

1.4 HUVC在不同金属切削变形区的受力分析

在HUVC过程中，为了体现HUVC的效果，需要刀具与工件不断分离接触，实现高频断续切削。为了满足分离条件，需要进给速度小于超声振子振幅的两倍，本文振子的振幅为20 μm，所以进给速度需要低于40 μm/r。由于进给速度为微米级，需要采用微加工理论，考虑切削过程中切削刃圆弧半径以及犁耕区对切削力的影响[15]。如图7所示，把金属切削变形区划分为弹性恢复区、剪切区、犁耕区和刀屑摩擦区四个变形区。

1.弹性恢复区 2.犁耕区 3.剪切区 4.刀屑摩擦区

图3中的切削力F和F为沿着整个切削刃分布的单位力的合力，包含四个切削区域的切削力。图7所示的切削过程可以简化成一个切削厚度为h(ε)、单位切削宽度为的正交切削过程，接下来，分别计算分布在这四个变形区内的单位力。

1.4.1 弹性恢复区

如图7区域1所示，工件材料为45号钢。根据材料弹塑性力学知识，弹性恢复的最大值可计算为：

式中：r为切削刃圆弧半径，r＝0.01 mm；τ为工件材料剪切屈服应力，τ＝106 MPa；σ为工件材料屈服强度，σ＝355 MPa；为工件材料杨氏模量，＝210 GPa。

根据弹塑性变形理论，当h(ε)＜0时，切削过后工件会完全复原，此时弹性恢复值等于h(ε)；当h(ε)＞0时，弹性恢复值等于弹性恢复最大值。因此，在切削过程中的弹性恢复值可计算为：

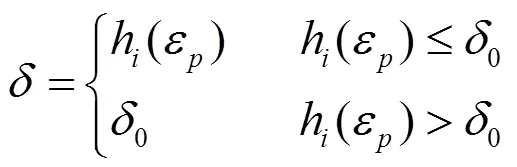
弹性恢复区的单元力分为正应力1和切应力1，由JEONG的理论[10]，后刀面上有：

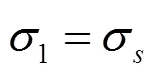
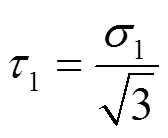
根据SHI的理论[13]，弹性恢复区内有：

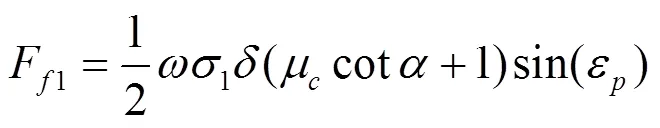
式中：F1、F1、F1依次为弹性恢复区内的主切削力、吃刀抗力、进给抗力，N；μ为后刀面摩擦系数，等于切应力对正应力的比值，μ＝0.577；为刀具后角。

1.4.2 犁耕区

如图8区域2所示，由SEONG提出的理论[14]可知，为区分剪切区与犁耕区的临界点。在点以下，发生弹性和塑形变形；点以上，发生剪切形变。因此，点以上为剪切区，点以下为犁耕区。有：

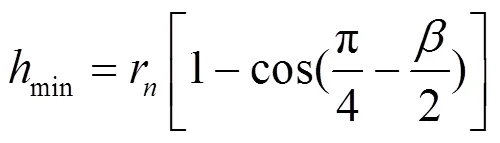
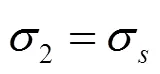
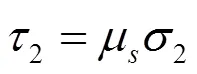
式中：min为最小切削厚度[14]，即点所在位置的切削厚度，mm；为刀具和工件的摩擦角，＝16.7°；μ为犁耕区的摩擦系数，μ＝0.3；2、2为犁耕区内的正压力和切应力[10]，MPa。

定义为单元力的角位置，得到：

式中：θ为当h(ε)＜min时，定义的一个犁耕区内的角度[14]；θ为当h(ε)＞min时，定义的一个角度。

综上，得到式（27）～式（29）。

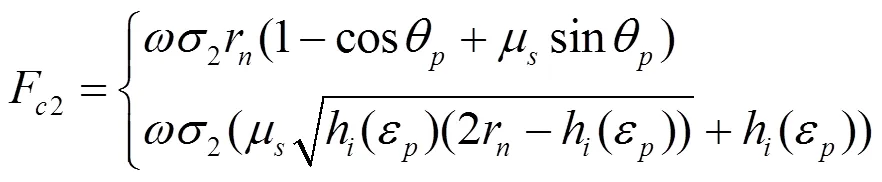
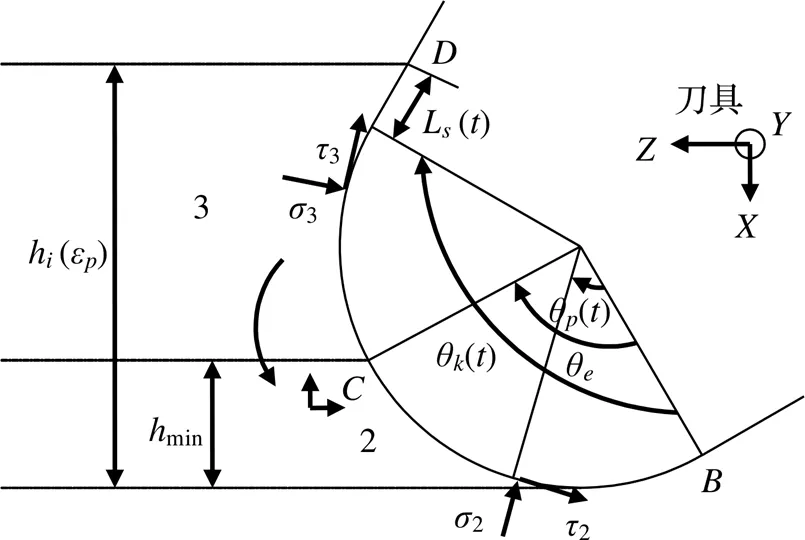
2.犁耕区 3.剪切区

1.4.3 剪切区

如图8区域3所示，为前角，当h(ε)＞min时，工件材料发生剪切形变。为了区分剪切区与刀屑摩擦区，定义一个点，在点以上为刀屑摩擦区，点到点之间为剪切区。在剪切区，当h(ε)≤r(1sin)时，剪切区为一段圆弧；当h(ε)＞r(1sin)时，剪切区为一段圆弧和一段直线。得到式（30）～式（33）[14]。

式中：F2、F2、F2依次为犁耕区内的主切削力、吃刀抗力和进给抗力，N。

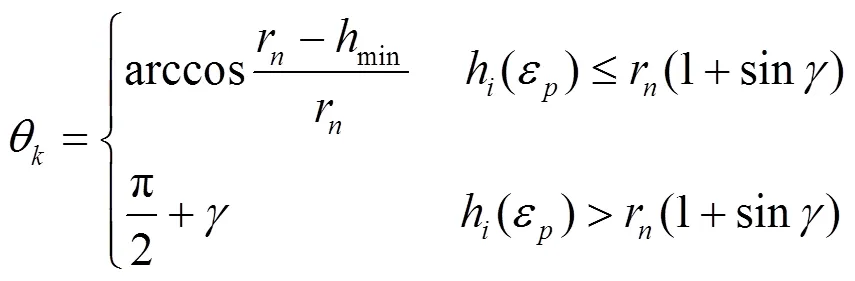
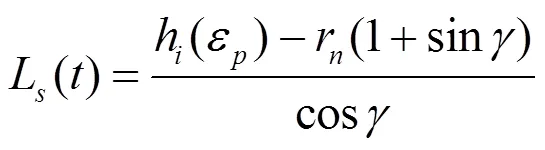
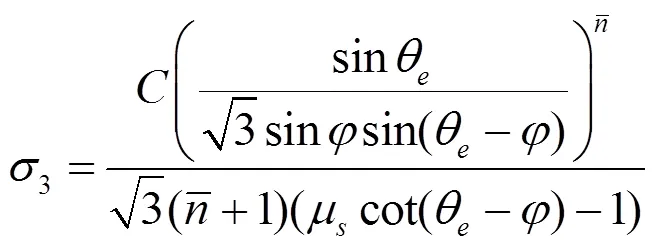
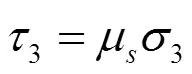
可由Merchant方程计算为：

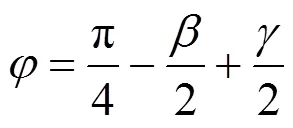
Ludwick方程描述了剪切区内的塑性形变过程，为：

h(ε)≤r(1sin)时，剪切区为一段圆弧，沿着圆弧的单元力计算见式（36）～式（38）。

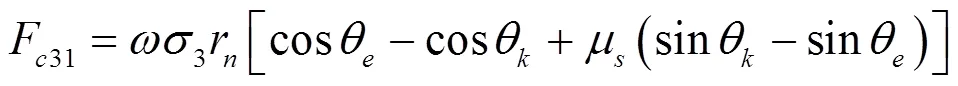
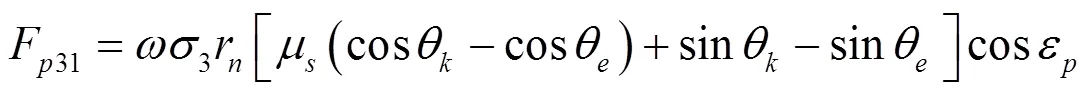
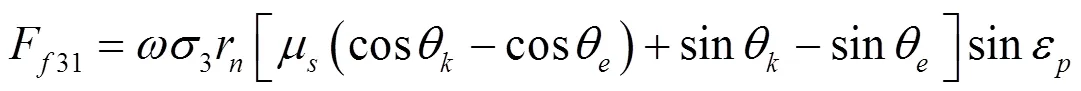
h(ε)＞r(1sin)时，剪切区为一段圆弧和一段直线，沿着直线的单元力计算为：

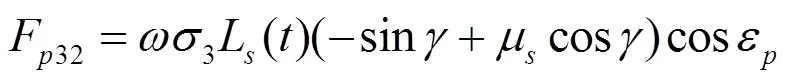
综上，当h(ε)≤r(1sin)时，有：

当h(ε)＞r(1sin)时，有：

式中：F3、F3、F3依次为剪切区内的主切削力、吃刀抗力、进给抗力，N。

1.4.4刀屑摩擦区

如图7区域4所示，当h(ε)≤min时，不会产生切屑，刀具前刀面与工件不会产生摩擦，此时，刀屑摩擦区内的切削力为0；当h(ε)＞min时，这个区域才会产生切屑，刀具前刀面与切屑发生摩擦，由于摩擦情况比较复杂，为了便于理论模型的建立，假定当切屑在前刀面上滑移时，不会发生冷焊和粘附效应。则有[10]：

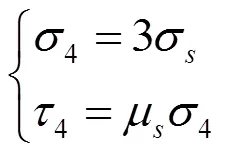
式中：4、4为刀屑摩擦区内的正应力和切应力。

根据OXLEY的理论[15]，有：

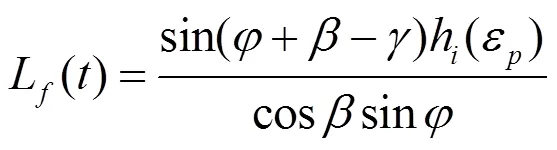
式中：L()为刀屑接触区的长度，mm。

当h(ε)≤min时，有：

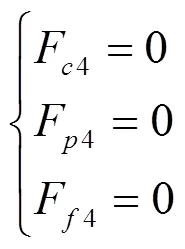
当h(ε)＞min时，有：

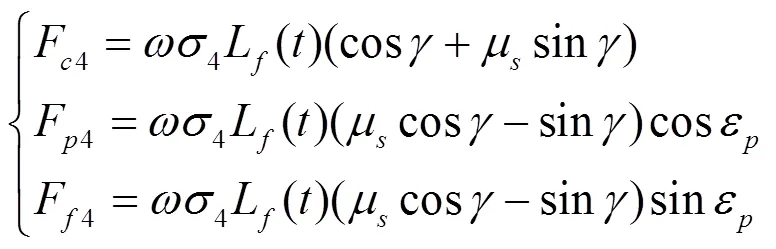
式中：F4、F4、F4依次为刀屑摩擦区内的主切削力、吃刀抗力、进给抗力，N。

综上，得：

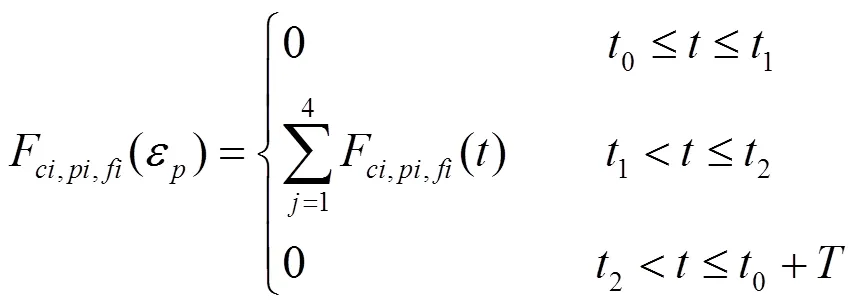
式中：F、F、F依次为在一个切削周期内，t时整个切削区域的总切削力、总吃刀抗力、总进给抗力，N。

2 实验

2.1 实验条件

实验装置如图9所示，实验采用弯振超声振子，超声振子沿着进给方向振动，频率为19.79 kHz，振幅为20 μm，采用杭州成功超声ZJS-2000型驱动电源，能够补偿频率和调频。

图9 实验装置图

实验采用Kistler9119AA1型测力仪，量程为0～4 kN，测量FFF三个力的测力仪敏感度分别为-7.5 PC/N、-7.5 PC/N、-3.7 PC/N，采样频率为6 kHz。

如图10所示，根据王进峰等[16]的研究结果，切削过程中圆弧切削刃可以近似为直线切削刃2，主偏角为k。

实验采用VCGT160402型刀具，刀尖尺寸如图11所示，刀尖圆弧半径＝0.2 mm，切削刃圆弧半径r＝0.01 mm，前角＝0°，后角＝7°，线段长度为1，1＝0.14 mm，直线切削刃对应的主偏角＝72.5°，由于切削过程中圆弧切削刃可以近似为直线切削刃，因此有：

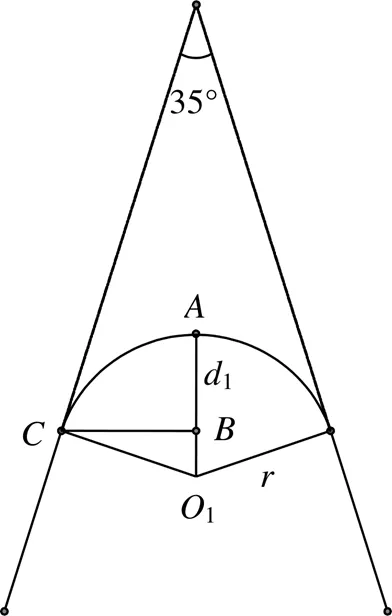
图11 刀尖尺寸

2.2 实验设计

设计实验验证理论模型的正确性。常规切削时关闭超声振子驱动电源，超声振子的振幅为0，高速超声振动切削时打开驱动电源，驱动频率为19.97 kHz，电压设置为300 V，超声振子振幅为20 μm。在做HUVC预实验的过程中发现，对比常规切削，刀具前角和后角对HUVC降低切削力的效果影响很小，而不同主偏角下HUVC降低切削力的效果有较大差异，因此，本文主要设计实验研究主偏角对HUVC切削力的影响。由式（49）可知，可以通过改变切深来改变切削过程中的主偏角。因实验采用VCGT160402型刀具，可知切削过程中最大主偏角接近72.5°。通过实验验证主偏角在0～65°变化时，相比常规切削，HUVC减小切削力的效果。主偏角k的取值如表1所示。

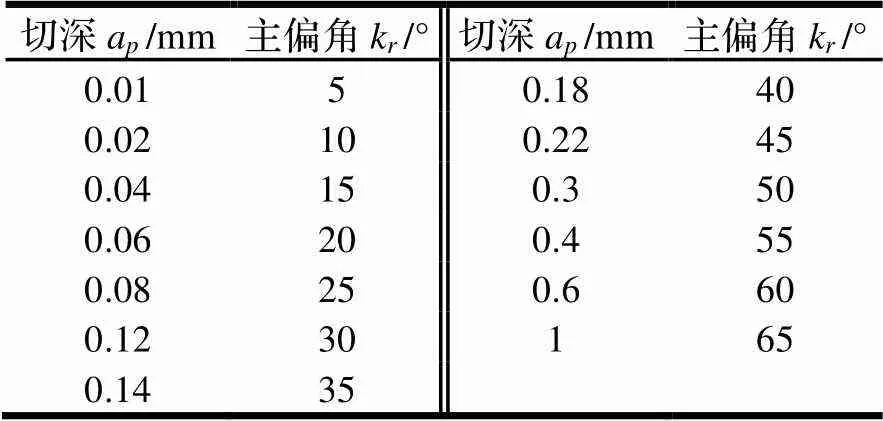
表1 主偏角的取值

选用26根45号钢工件，由于刚购买回来的工件本身存在径向不圆，在正式实验前对工件进行修圆，用较高的切削速度和较小的进给量和背吃刀量对工件反复车削修圆，直到能产生连续切屑，工件直径统一修圆为30 mm。

实验过程中，每两个工件为一组，分别进行HUVC和常规切削，共13组实验。首先用测力仪测量HUVC和常规切削在5°～65°不同主偏角下的平均主切削力、平均进给抗力和平均吃刀抗力；然后计算相比常规切削，HUVC在不同主偏角下各实验平均切削力减小效果，与理论力学模型预测结果对比，验证模型的有效性。

3 结果与讨论

3.1 理论力学模型预测结果

由于实验设计的主偏角变化范围为5°～65°，因此理论模型主偏角变化范围也设置为5°～65°，理论模型切深的设置与表1中切深的设置保持一致，其他参数一样。根据上述理论力学模型，首先计算主偏角在5°～65°变化时，HUVC与常规切削的理论平均主切削力、吃刀抗力和进给抗力；然后，对比常规切削，求出HUVC在不同主偏角下各理论平均切削力理论减小百分比。

相比常规切削，HUVC各理论平均切削力减小百分比如图12所示。在不同主偏角下，HUVC各理论平均切削力与常规切削各理论平均切削力的大小可描述为：

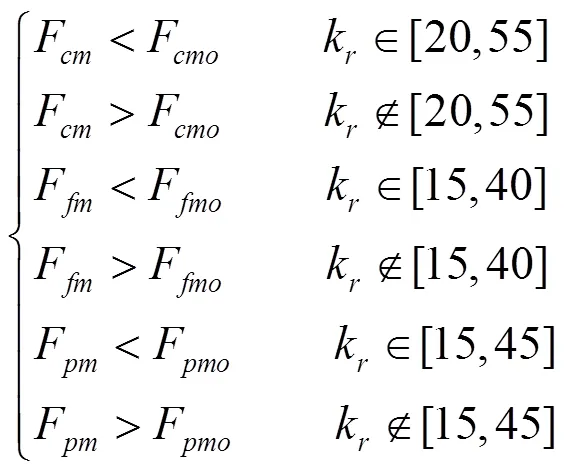
式中：Fcm、Ffm、Fpm依次为HUVC理论平均主切削力、进给抗力、吃刀抗力，N；Fcmo、Ffmo、Fpmo依次为常规切削理论平均主切削力、进给抗力、吃刀抗力，N。

理论预测结果表明，相比常规切削，主偏角k变化范围为20°～55°时，F＜F，HUVC能体现出降低切削力的效果，且主切削力最大减小百分比为25%；当主偏角不在这个范围内时，HUVC主切削力大于常规切削主切削力，HUVC不能体现出降低切削力的效果，丧失HUVC的优越性。因此，对于HUVC主切削力而言，主偏角适用范围理论上为20°～55°，同理，进给抗力、吃刀抗力的主偏角适用范围理论上依次为15°～40°、15°～45°。

3.2 实验结果与讨论

F、F、F分别为HUVC实验平均主切削力、进给抗力、吃刀抗力，N；F、F、F分别为常规切削实验平均主切削力、进给抗力、吃刀抗力，N。

对比F，F减小百分比如图13所示。实验结果表明，当主偏角变化范围为20°～55°时，F＜F；在5°～65°主偏角变化范围内，F减小百分比与F减小百分比相符合。相比F减小百分比，F减小百分比低于理论预测值，是由于上述理论力学模型对切削区域的受力及变形做了简化处理，也对圆弧刀尖主偏角做了简化处理；同时未考虑刀屑摩擦区的冷焊和粘附效应；此外，实际切削过程中，机床性能的稳定性以及超声振子驱动电源性能的稳定性都会影响切削力，使得实验测出来的切削力和理论值有偏差，但在误差允许范围内，HUVC实验平均主切削力减小百分比与理论预测值接近。实验结果表明，对于HUVC主切削力而言，主偏角适用范围为20°～55°，与理论预测的主偏角适用范围相符合。

图13 HUVC平均主切削力对比图

对比F，F减小百分比如图14所示。实验结果表明，当主偏角变化范围为15°～40°时，F＜F；在5°～65°主偏角变化范围内，F减小百分比与F减小百分比相符合。相比F减小百分比，部分F减小百分比高于理论预测值。这可能是因为切削热的影响，上述理论力学模型未考虑切削过程中切削热对切削区域应力应变的影响，超声振动切削为高频断续切削，在切削过程中，刀具与工件不断的分离接触，在分离过程中，空气流进到刀具与工件之间的间隙，能够起到减小切削热的作用，从而减小切削区域的应力应变，使得实验过程中HUVC减小切削力的效果比理论预测好，但在误差允许范围内，实验平均进给抗力减小百分比与理论预测结果接近。实验结果表明，对于HUVC进给抗力而言，主偏角适用范围为15°～40°，与理论预测的主偏角适用范围相符合。

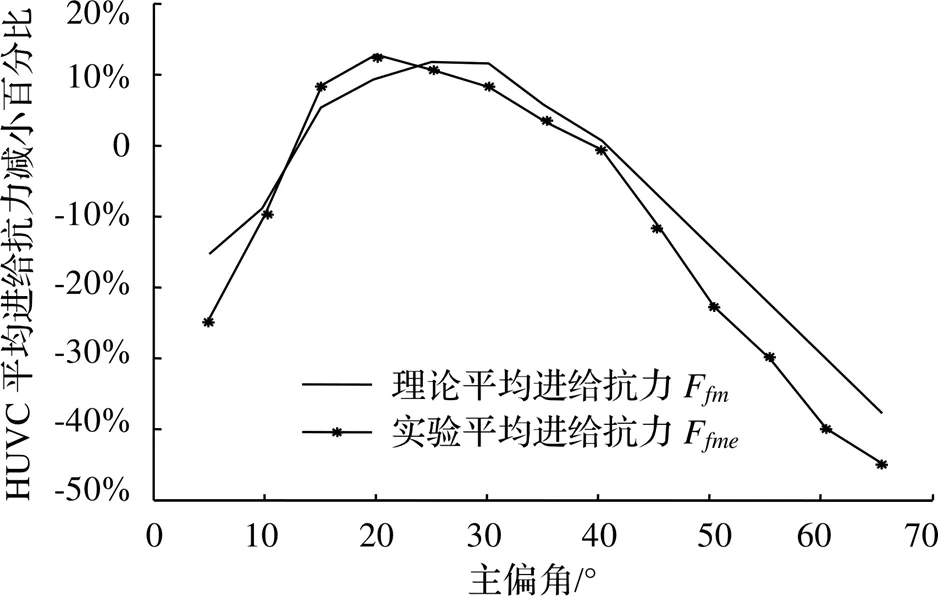
图14 HUVC平均进给抗力对比图

对比F，F减小百分比如图15所示。实验结果表明，当主偏角变化范围为15°～45°时，F＜F；在5°～65°主偏角变化范围内，F减小百分比与F减小百分比相符合，在误差允许范围内，实验平均吃刀抗力减小百分比与理论预测结果接近。实验结果表明，对于HUVC吃刀抗力而言，主偏角适用范围为15°～45°，与理论预测的吃刀抗力适用范围相符合。

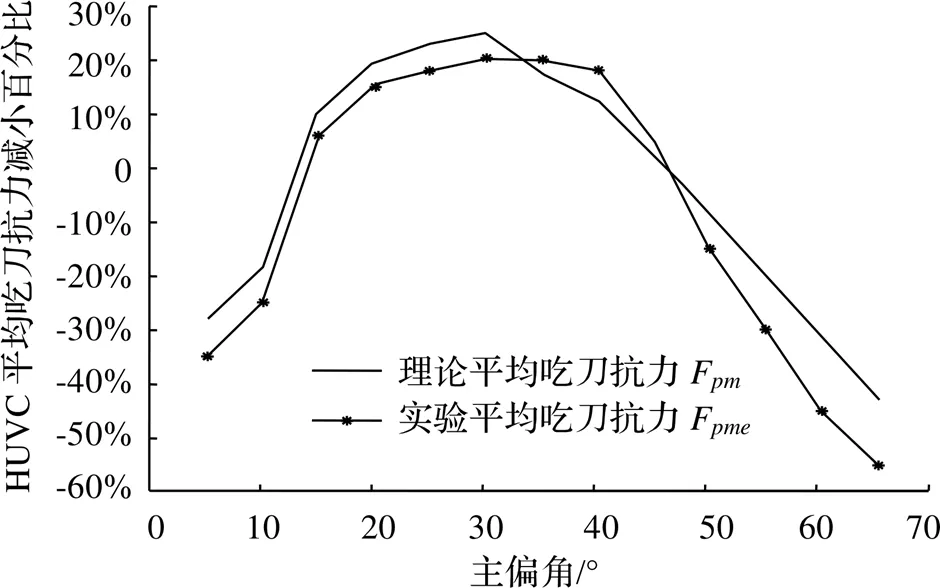
图15 HUVC平均吃刀抗力对比图

综合以上理论预测结果与实验结果可知，在误差允许范围内，实验结果与理论结果相符合，实验规律与理论预测规律相一致，故验证了理论模型的有效性。

4 结论

本文建立了高速超声振动切削在0～90°主偏角下的切削力模型，并设计实验验证理论力学模型的有效性，同时对比常规切削，得到了高速超声振动切削在不同主偏角下减小切削力的百分比，主要结论如下：

（1）在5°～65°主偏角变化范围内，HUVC各实验平均切削力减小规律与理论预测规律相符合；在误差允许范围内，HUVC各实验平均切削力减小百分比与理论预测结果接近，验证了理论力学模型的有效性；

（2）对于主切削力而言，HUVC适用主偏角范围为20°～55°；对于进给抗力而言，HUVC适用主偏角范围为15°～40°；对于平均吃刀抗力而言，HUVC适用主偏角范围为15°～45°。因此，为了使得HUVC的切削效果达到最佳，HUVC的主偏角适用范围为20°～40°。

[1]隈部淳一郎. 精密加工振动切削[M]. 北京：机械工业出版社，1985：19-29.

[2]MORIWAKI T，SHAMOTO E. Ultrasonic Elliptical Vibration Cutting[J]. CIRP Annals， 1995，44 （1）：31-34.

[3]Ma C X，SHAMOTO E，MORIWAKI T，et al. Study of Machining Accuracy in Ultrasonic Elliptical Vibration Cutting[J]. International Journal of Machine Tools & Manufacture，2004，44（12）：1305-1310.

[4]XIAO M，Wang Q M，SATO K，et al.. The Effect of Tool Geometry on Regenerative In-stability in Ultrasonic Vibration Cutting[J]. International Journal of Machine Tools & Manufacture，2006，46（5）：492-499.

[5]王致坚，刘舜尧. 振动切削在螺纹加工中的应用[J]. 机械，2007，34（8）：45-46.

[6]BREHL D E，DOW T A. Review of Vibration-assisted Machining[J]. Precision Engineering，2008，32（3）：153-172.

[7]Sui H，Zhang X Y，Zhang D Y，et al.. Feasibility Study of High-speed Ultrasonic Vibration Cutting Titanium Alloy[J]. Journal of Materials Processing Technology，2017（247）：111-120.

[8]DORLIN T，FROMRNTIN G，COSTESJ P. Generalised Cutting Force Model including Contact Radius Effect for Turning Operations on Ti6Al4V Titanium Alloy[J]. The International Journal of Advanced Manufacturing Technology，2016，86（9-12）：3297-3313.

[9]CRICHIGNO FILHO J M. Applying Extend-ed Oxley’s Machining Theory and Particle S-warm Optimization to Model Machining Forces[J]. The International Journal of Advanced Manufacturing Technology，2017，89（1-4）：1127-1136.

[10]JEONG D K，KIM D S. Theoretical Analysis of Micro-cutting Characteristics in Ultra-precision Machining. Journal of Materials Processing Technology，1995，49（3-4）：387-398.

[11]BAI W，SUN R L，Gao Y，et al.. Analysis and Modeling of Force in Orthogonal Elliptical Vibration Cutting[J]. The International Journal of Advanced Manufacturing Technology，2016，83（5-8）：1025-1036.

[12]NATEGH M J，RAZAVI H，ABDULLAH A. Analytical Modeling and Experimental Investigation of Ultrasonic-vibration Assisted Oblique Turning[J]. International Journal of Mechanical Sciences，2012，63（1）：1-11.

[13]SHI T. Micro Machining Technology[M]. Beijing：China Machine Press，2011：45-54.

[14]SEONG M S，LIM H S，AHN J H. Effects of the Friction Coefficient on the Minimum Cutting Thickness in Micro Cutting[J]. International Journal of Machine Tools & Manufacture，2005，45（4-5）：529-535.

[15]OXLEY P L B，HASTINGS W F. Minimum Work as a Possible Criterion for Determining the Frictional Conditions at the Tool/Chip Interface in Machining[J]. Philosophical Transactions of The Royal Society of London，1976，282（1310）：565-584.

[16]王进峰，商正，吕鹏瑞，等. 刀尖圆弧半径对主偏角影响的分析与实验研究[J]. 图学学报，2019，40（2）：256-260.

The Most Applicable Tool Cutting Edge Angle Range of High-Speed Ultrasonic Vibration Cutting

XU Jiye，TU Jun，YU Deping

( School of Mechanical Engineering, Sichuan University, Chengdu 610065, China )

In order to study the effect of tool cutting edge angle on cutting forces during high-speed ultrasonic vibration cutting (HUVC), the theoretical model of HUVC was established. Firstly, the distribution of cutting forces of HUVC at different tool cutting edge angles was analyzed. Then the cutting thickness, unit cutting width of different cutting areas and the cutting forces of four metal cutting deformation zones were calculated. Finally, the cutting force model of HUVC was built with the tool cutting edge angles of 0 to 90°. The theoretical and experimental results indicates that when the tool cutting edge angle varies from 20° to 55°, the principal cutting force is smaller than that of the conventional cutting. For the feed thrust force, the tool cutting edge angle is applicable from 15° to 40°. For the radical thrust force, the tool cutting edge angle is applicable from 15° to 45°. In order to achieve the best cutting effect of HUVC, the most applicable tool cutting edge angle is supposed to be from 20° to 40°.

high-speed ultrasonic vibration cutting；tool cutting edge angle；cutting force；straight cutting edge；micro-machining

TG663

A

10.3969/j.issn.1006-0316.2020.07.009

1006－0316 (2020) 07－0052－11

2020－02－18

国家自然科学基金项目（51875372）

徐继业（1994－），男，河南驻马店人，工学硕士，主要研究方向为超声振动切削。

余德平（1987－），男，江西抚州人，博士，博导，主要研究方向为超精密加工与等离子技术，E-mail：4849007@qq.com。