基于改进蚁群算法的人机象棋平面路径规划

朱晨曦，高军伟，房国栋，孔德帅

（青岛大学 自动化学院，青岛266071）

作为娱乐机器人的分支，人机象棋正逐渐成为研究的热点。棋盘中，棋子仅存在2 种移动，一种按走法，另一种被吃掉后放于指定位置。目前，人机象棋执行多为机械臂实现的棋子空间移动，无需考虑障碍。为提高设备环境适用性，因此研究人机象棋

平面避障路径问题具有重要意义。

蚁群算法作为一种寻优算法，广泛应用于解决实际路径问题。针对算法局部解及收敛等问题，文献[1]将信息素分布限制在固定区间内，算法性能不受信息素下界的影响；文献[2]建立α 与β 的互锁关系，使其动态自适应调整；文献[3]引入最大最小蚂蚁系统，避免蚁群算法早熟停滞；文献[4]引入动态局部优化搜索策略，针对蚁群不同路径使用不同信息素，提高了路径质量；文献[5]提出禁忌搜索的蚁群改进算法，优化了初始信息浓度，避免局部最优解。

在此结合人机象棋与蚁群算法，针对蚁群算法局部解及收敛问题，改进启发因子；针对棋子和障碍同尺寸问题，对所得最优路径进行控制点精简，减少拐角次数，缩短棋子移动距离。

1 算法描述

1.1 环境建模

为使棋子平面移动时避开障碍棋子，计算机处理棋盘图像得到10×9 棋盘数字矩阵后，调用博弈算法获得棋局下一步走法，再经蚁群算法规划路径，由机械臂实现棋子平面避障移动。

人机象棋平面博弈系统，由机器视觉、博弈算法、路径规划、机械臂执行4 个部分组成。在此，路径规划采用了栅格法对棋局进行离散化处理。对博弈算法当前调用的10×9 棋盘数字矩阵实时扩充，有棋子的位置置1，其余位置均以0 填充，最终得到一个20×20 的0 1 矩阵并栅格化，以避免极端情况下，除90 个棋盘横纵线交叉点[6]所在栅格本身外，相邻两交叉点各自所在栅格间仍有栅格可供路径移动。

考虑象棋外观尺寸，粒子和障碍物面积应该都按照象棋大小膨胀[7]。设置栅格边长a＝1，栅格建立时，可将整个棋盘空间划分成400 个大小相同的栅格，各栅格从左至右、自上而下依次编有序号。序号与坐标系的关系为

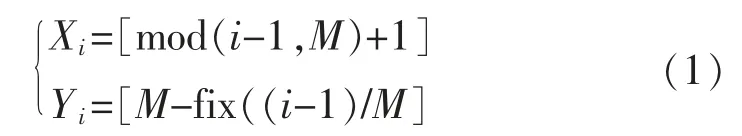
式中：i 为栅格编号；M 为单行栅格个数；mod（）为取余；fix（）为向零方向取整作商；Xi和Yi为栅格中心的坐标位置。

棋盘栅格建立后，相邻栅格中心距离dij为1 或1.414，故移动棋子被当做二维平面中质点时，为避免与障碍棋子发生碰撞，质点只能在上下左右4 个方向移动。移动前后栅格应满足：

式中：i 为质点当前栅格；j 为质点下一栅格；map（j）为非障碍栅格；dij为栅格i 与栅格j 之间距离。棋盘扩充后的栅格坐标系如图1 所示。

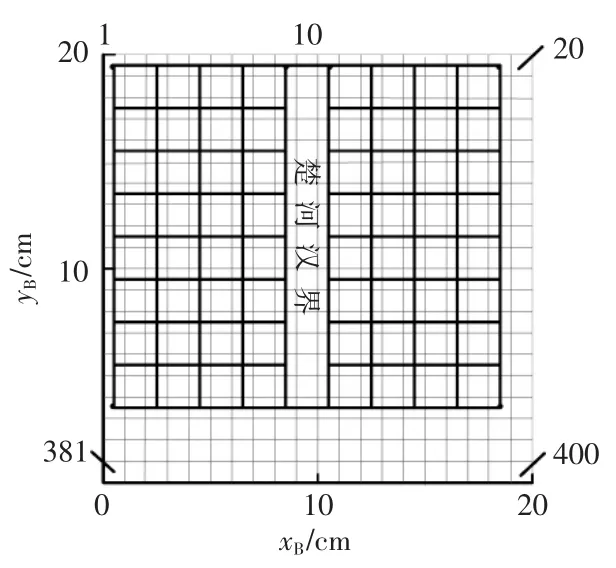
图1 棋盘扩充后栅格坐标系Fig.1 Grid coordinate system after checkerboard expansion

1.2 常规蚁群算法

常规蚁群算法概率选择方式主要根据节点之间的信息素浓度和启发信息来确定。环境建模后，初始化数据进行迭代，蚂蚁根据信息素随机寻找路径直到终点，找到最优路线后更新信息素，直至迭代完成。

棋盘栅格化后，由蚁群算法得出的转移概率即为相邻栅格中心节点间的选择概率[8]。在t 时刻，蚂蚁k 从yi转移到yj的概率为

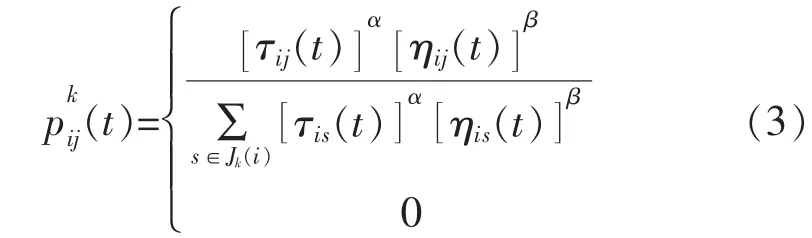
式中：α 为信息素浓度相对重要程度；τij（t）为信息素浓度；β 为启发性因子相对重要程度；ηij（t）为实际距离的倒数。

2 改进蚁群算法

2.1 启发矩阵改进

常规启发式信息矩阵为节点i 到下一节点j 实际距离倒数，未考虑终点栅格E 的影响。栅格中，棋子从i 到j 水平或竖直移动时路径等长，因此ηij＝1/dij在棋盘环境中没有效果。为增加算法收敛能力，需要对其进行改进，在此引入常量a 和b 对djE进行初等变换，即

式中：djE为下一节点j 与目标节点E 之间的实际距离。然后通过棋盘试验结果，选择同时满足路径最短和收敛代次最少的a，b 值。

2.2 信息素的更新策略

马和象类棋子按走法移动时，障碍棋子不能出现在绊马脚和塞象眼的位置。为配合djE，棋子向对角靠拢，引入“热区”概念，热区是指当前节点与目标节点为对角线的矩形区域。当前节点i 向下一节点j 随机搜索时，选择热区节点的概率会比非热区节点大，可减少不必要方向的搜索[9]。

式中：λ 为常量参数；i 为每次更新的当前节点；j 为下一节点。

2.3 最优路径保留

蚁群算法在随机搜索路径过程，可能会丢失曾搜索到的最优路径，即本次最短路径在下次迭代中未出现。棋盘常规蚁群的仿真收敛曲线如图2 所示，收敛过程中最优路径丢失。

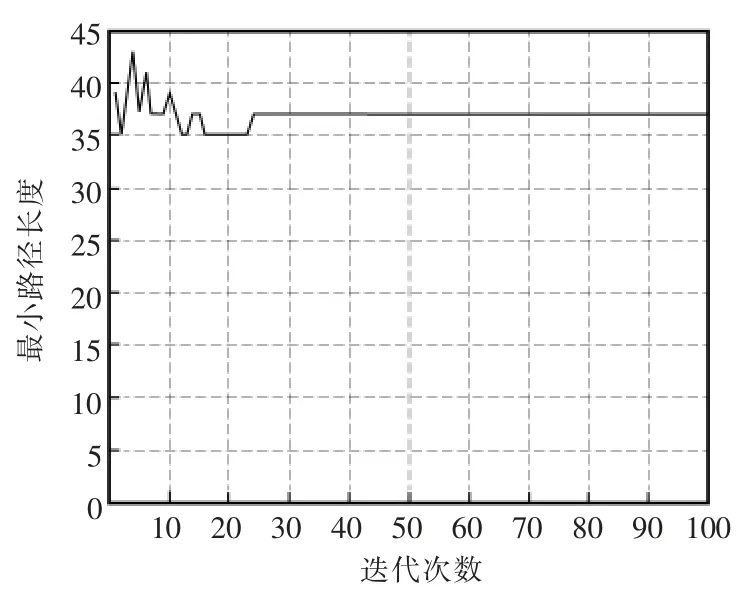
图2 最优路径长度Fig.2 Length of the optimal path

路径中，信息素遵循新增和挥发规则，最优路径的丢失会降低该路径信息素浓度[10]。为提高算法性能，在每次迭代得到最优路径后，都与前次迭代最优路径进行比较。若长度大于前代最优路径，则将前代最优路径加入在本次迭代路径，在前代最优路径得以保留的同时，增加算法向已得最优路径的收敛。

2.4 已得路径的平滑处理

在棋盘栅格中设定棋子仅水平或竖直移动，会导致拐角次数的增多。为减少不必要控制点，缩短棋子移动距离，需对已得路径进行控制点精简，优化已有路径的整体走向[11]。控制点精简如图3 所示，在此仅为图1 所示坐标系的局部示意图。

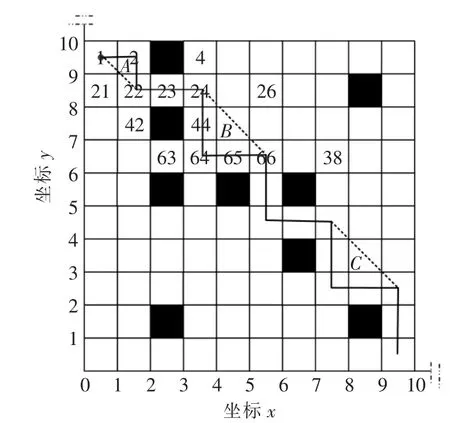
图3 控制点精简示意图Fig.3 Diagrammatic sketch of reduced control pointn

图3 中，A，B，C 拐角位置皆可由虚线路径代替。循环精简从第1 个控制点1 开始，依次与其后面所有非相邻栅格控制点（第3 个控制点22 到目标控制点E，图中未标出点E）连接成虚线路径，根据点到直线距离公式，计算当前虚线点1—点22 到全部障碍物中心最短距离d。若d 都不小于则点1—点22 成为新的可行路径，此段原先控制点被抹除，并从尾点22 开始新层循环，否则不做修改，直至最后。为此，引入变量L，L 为是/否生成新路径：L=1，生成；L=0，不生成。L 值为

式中：d 为障碍物中心点距离直连虚线路径最短距离；a 为栅格边长。

2.5 蚁群算法改进流程

步骤1对实时棋盘10×9 数字矩阵进行扩充，并采用栅格法对结果栅格化。

步骤2将实时棋子始末移动位置换算成栅格号，初始化算法参数。

ⅰ.蚂蚁开始路径选择，按热区寻找下一可行节点j，仅水平或竖直方向移动，得出本次迭代的最优路径；

ⅱ.若本次迭代的最优路径长于上次迭代最优路径，则上代最优路径加入本次路径，共同进行信息素更新。

步骤3全部迭代完成后得出最优路径。

步骤4栅格中心控制点精简方法。将最优路径中每个控制点依次与其非同一直线上的后面所有控制点都分别连接成待生成新路径。

ⅰ.通过点到直线距离公式得出d 的大小，判断所有待生成路径是否符合新路径生成条件。如果当前待生成路径都不符合条件，返回步骤4，否则继续步骤4ⅱ。

ⅱ.删除此段之前中间控制点和路径，由新生成路径替代。

ⅲ.返回步骤4，循环完成每段新生成路径。

步骤5输出完整新生路径。

3 试验结果仿真

为验证改进蚁群算法对棋盘栅格中棋子路径规划的有效性，以棋子被吃掉后从当前位置移至棋局外指定位置为例，通过MatLab 2014a 对其仿真。考虑到参数取值对算法性能的影响[12]，设置α=1.5，β=4.1，ρ=0.64，m=30，Q=14。

3.1 算法改进仿真

20×20 棋盘栅格环境中，对基本蚁群算法和对a=1，b=1 的启发因子及信息素更新策略改进的蚁群算法进行路径仿真，仿真结果如图4 所示。

图4 仿真结果Fig.4 Simulation results

MatLab 运行20 次后的统计路径结果见表1。

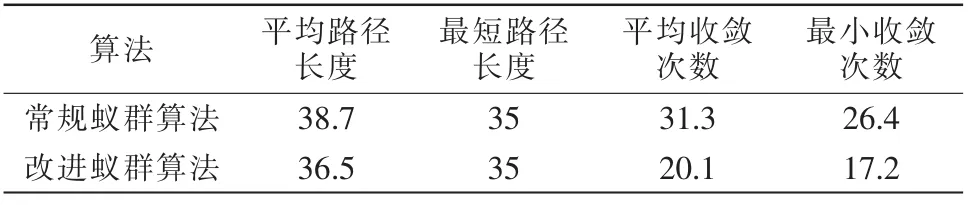
表1 算法改进前后运行20 次的路径结果统计Tab.1 Path result statistics of 20 runs before and after algorithm improvement

由表可知，相较于常规蚁群算法，信息素更新策略改进后的蚁群算法平均路径长度降低5.9%，平均收敛次数降低36.1%，最短路径长度虽无变化，但最小收敛次数降低34.8%，改进后的蚁群算法在平均路径长度和收敛速度上比常规蚁群算法更有优势。a，b 取不同值后，对改进蚁群算法循环20 次，路径结果统计见表2。

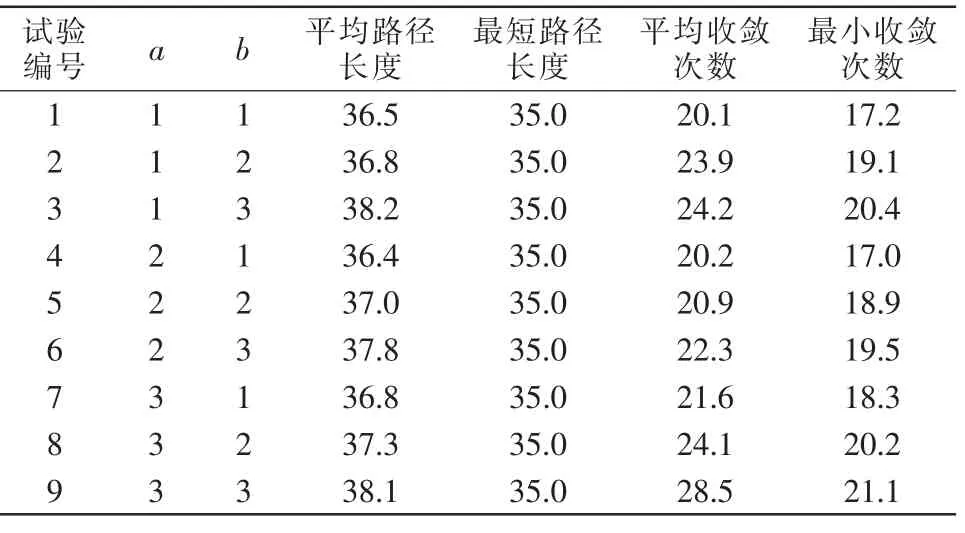
表2 a，b 取值不同时改进蚁群算法路径结果统计Tab.2 Path result statistics after improving ant colony algorithm with different values of a and b

由表可知，a=1，b=1 时平均收敛次数最小；a=2，b=1 时平均路径最短，且最少收敛次数最小。与常规蚁群算法相比，a=2，b=1 时改进蚁群算法具有更好性能，平均路径长度减少6.0%，平均收敛次数降低35.6%。

3.2 已得路径的平滑仿真

在棋盘栅格20×20 环境中，路径控制点精简后路径长度23.9，比精简前最短路径长度35.0，减少31.7%；中间控制点从15 精简到5 个，减少66.7%。棋子运动轨迹的仿真如图5 所示。

4 结语

利用改进的蚁群算法求解棋子移动路径，改进包括对启发矩阵及信息素更新策略的改进，对棋子多拐角多控制点问题的改进。改进后进一步提高了收敛速度，缩短了移动距离，能让棋子在平面移动中实现良好的人机对弈过程，增加适用性。

图5 路径控制点精简Fig.5 Path control point reduction