基于PSO-BP神经网络的网络时延预测算法

时维国，雷何芬

（大连交通大学 电气信息工程学院，大连116028）

网络控制系统NCS（networked control system）中传输时延受到通信网络协议、节点驱动方式、路由算法等因素影响，呈现出随机变化的非线性特性[1-2]。针对NCS 时延问题，文献[3-6]通过对NCS 中时延数据的分析处理，来建立数学模型对网络时延进行预测。尽管数学模型能够准确地表达输入与输出之间的函数关系，但由于网络时延具有随机性，很难准确地对其进行建模，而神经网络算法是以神经元为基础模拟人脑的计算模型，可以映射和逼近很多函数，无需对样本进行分析建立数学模型，如文献[7-10]采用神经网络对NCS 时延进行预测。在众多神经网络算法中，由于BP 神经网络BPNN（back propagation neural network）具有网络结构比较简单，神经元个数少，运算量小等优点，在预测方面有着很多的应用。

图1 单隐层BPNN 结构Fig.1 Single hidden layer BPNN structure

在此，采用BPNN 算法对NCS 时延进行预测，针对BPNN 收敛速度慢，易陷入局部极值的问题，利用粒子群算法PSO 优化BPNN 中的初始权值和阈值来改善BPNN 的性能，提高算法收敛性，避免陷入局部极值点。

1 时延数据的采集及处理

1.1 时延数据的采集

在此采用Ping Tester Pro 软件，对从某大学实验室（IP 地址为192.168.43.136）访问到某知名网站（IP 地址为39.156.66.18） 的时延数据进行采集，将采集的500 组时延数据导出作为试验数据。此次网络采集采用电脑连接手机热点，因NCS 中传感器采用时间驱动，故将软件中参数设置为固定间隔发送，数据包大小为32 B。

1.2 时延数据的归一化

数据的归一化就是把需要处理的数据通过算法处理后，将数据限制在需要的一定范围内。数据的归一化的目的是为了后续数据处理的方便和保证程序运行时快速收敛。在此，采用了最大最小标准化的归一化方法，将样本数据映射到数值［0，1］之间。其公式为

式中：x 为样本数据；min（x），max（x）分别为样本数据中的最小值、最大值；x′为数据归一化后的数值。

2 粒子群优化的BPNN 算法

2.1 BP 神经网络

BPNN 是在1986年由David E.Rumelhart 等学者提出的，是一种按照误差逆向传播算法训练的多层前馈神经网络。BPNN 由输入层、隐含层、输出层组成，每一层之间各神经元相互独立不连接，而层与层之间的神经元相互连接。其原理是误差的反向传播采用梯度下降法更改网络的连接权值和阈值，最终使网络的实际输出值与期望输出值的误差均方值达到要求的精度。单隐层BPNN 结构如图1 所示。

图中，i 为输入层的数目；j 为隐含层的数目；k为输出层的数目；y 为BPNN 的实际输出；yp为期望输出；ωij为输入层第个节点到隐含层第个节点之间的连接权值；ωjk为隐含层第个节点到输出层第个节点之间的连接权值；θj为隐含层第个节点的阈值；θk为输出层第个节点的阈值。

BPNN 包含数据传输的前向通道和误差的反向计算。在数据传输的前向通道过程中，数据经输入层的神经元处理后与ωij进行计算，其计算结果作为隐含层神经元的输入，隐含层神经元的输出与ωjk计算后作为输出层神经元输入，输出层神经元的输出即为BPNN 的输出。将BPNN 的输出值与期望值比较计算误差。若误差满足设定的精度要求，则不进行误差的反向计算； 否则需进行误差的反向计算，通过梯度下降法改变各层神经元之间的连接权值和神经元的阈值，直至达到设定的误差精度，或达到最大迭代次数停止计算。

2.2 粒子群算法

粒子群算法是一种群体智能的优化算法，最早是在1995年由Kennedy 和Eberhart 提出。在PSO优化算法中，将所有的优化类问题当做鸟群的捕食行为进行分析，鸟群中的一只鸟代表着优化问题中的一个潜在的解，即PSO 算法中的一个粒子。鸟类在捕食的行为中会根据同伴的方向、速度来不断地调整自己的位置，即PSO 中的粒子会根据适应值调整自己的速度和位置迭代找到最优解。

PSO 算法中，粒子的当前特征可以通过粒子自身的适应值表示其优劣程度，粒子的搜索状态用其当前位置和速度表示。Pb为个体粒子在自身历史的适应值中为最优的值所对应的位置；Gb为所有粒子在历史的适应值中为最优值所对应的位置。粒子的适应值随迭代而更新，将新的适应值与自己过去的最优的适应值Pb比较，如果新的适应值比Pb对应的适应值小，则将新的适应值对应的位置赋值给Pb，再将Pb对应的适应值与Gb对应的适应值比较，若Pb对应的适应值比较小，则用Pb赋值给Gb，成为当前全局最优的位置。

假设，PSO 算法中，有H 个粒子组成一个种群，每个粒子的维度为N，xh为种群中第h 个粒子的位置，即xh=（xh1，xh2，…xhN），h＝1，2，…，H；vh为种群中第h 个粒子的速度，即vh=（vh1，vh2，…vhN）。

确定PSO 算法中求适应值大小的目标函数，根据目标函数求出粒子的适应值大小，通过比较适应值大小确定粒子的当前最优位置和群体最优位置。第h 个粒子的当前最优位置为Pbh；群体的当前最优位置为Gbh。即

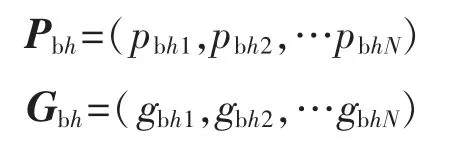
在PSO 算法中，粒子通过当前最优位置和群体最优位置，在每次的迭代中更新自己的速度和位置。PSO 算法公式为

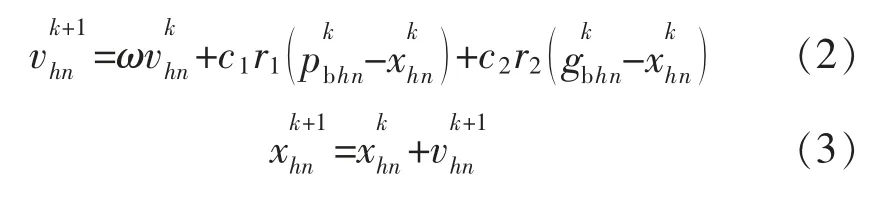
其中

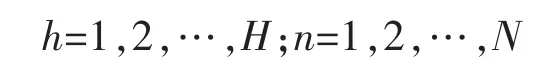
式中：ω 为惯性权重，其值的大小影响着粒子的全局和局部的寻优能力；k 为粒子的当前迭代次数；c1和c2为粒子的学习因子，其值大小影响着粒子的收敛性；r1和r2为选取的［0，1］之间的随机数。PSO 算法中需对粒子的位置和速度设置合理范围。PSO 算法的迭代停止条件为粒子达到最大迭代次数或适应值大小满足设定的要求。

2.3 PSO-BPNN 的时延预测模型

BPNN 算法对网络连接权值和阈值的初始值很敏感，在相同条件的下对BPNN 赋予不同初始值的网络连接权值和阈值，BPNN 会表现出不同的收敛速度。网络连接权值和阈值的初始值离极值点近则收敛速度快；网络连接权值与阈值的初始值离极值点远则收敛速度慢。

PSO 算法是一种不断学习的优化算法，只需通过更新粒子的速度和位置就能实现对解空间的全局搜索从而得到最优解，算法简单且效率高。PSO优化BPNN 的基本思想是：将BPNN 的连接权值和阈值的初始值当成PSO 算法中的一个粒子，粒子的维度等于权值的个数加阈值的个数之和，取测试样本的BPNN 的输出值与实际期望值差值的平方和为PSO 算法的中适应值函数，对BPNN 的初始连接权值和阈值进行优化，利用优化后PSO 算法的输出值作为BPNN 的初始连接权值和阈值对样本数据进行训练。

2.3.1 PSO-BPNN 的时延预测基本步骤

步骤1将测得500 组时延数据做归一化处理后分为样本数据400 组，测试数据100 组。

步骤2初始化BPNN。确定BPNN 的网络结构、各层神经元处理函数，给各参数赋初值。

步骤3初始化PSO 算法。随机选取H 组满足BPNN 初始权值和阈值要求的粒子，并给PSO 算法中其他参数赋初值；将测试数据通过BPNN 的正向传播的输出值与期望值之间的差值的平方和作为PSO 算法的适应值函数。

步骤4计算粒子的适应值。

步骤5判断粒子的迭代次数。若粒子的迭代次数未达到设定值，则根据式（2）和式（3）更新粒子的速度、位置，且迭代次数加1，再将更新的粒子返回步骤4 重新计算粒子的适应值； 若迭代次数达到设定值，则停止迭代，输出PSO 算法中群体最优位置Gb。

步骤6获取最优权值和阈值。将PSO 算法中群体最优位置Gb赋值给BPNN 作初始权值和阈值。

步骤7计算误差。将PSO 算法优化过的初始权值和阈值的BPNN 对400 组样本数据进行训练。选取BPNN 的输出值与期望值之间的差值的平方和作为误差函数。

步骤8判断满足条件。将误差值与设定值比较，若误差值没有达到设定的精度，则采用误差的反向传播通道更新BPNN 的权值和阈值；若误差值达到设定的精度则输出BPNN 的输出。

PSO-BPNN 的流程如图2 所示。

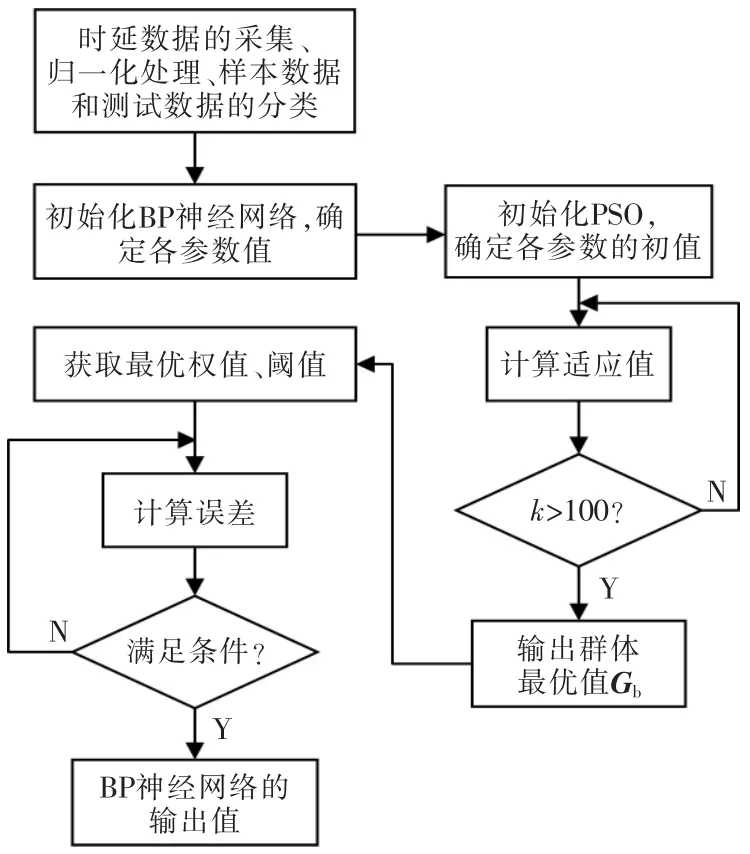
图2 PSO-BPNN 的流程Fig.2 PSO-BPNN flow chart

2.3.2 PSO-BPNN 时延预测的参数设置

在此，选取前2 个时刻时延数据来预测下一时刻的时延数据，即BPNN 输入层神经元数为2 个，输出层神经元数为1 个。文献[11]表明，BPNN 隐含层个数为1 时可以对任意精度的函数进行逼近。故在此BPNN 选取单隐含层，隐含层神经元的个数由进行选取，当取a＝9 时，l＝10，即隐含层神经元的个数为10。隐含层的神经元函数选为“logsig”，输出层神经元函数选为“logsig”。BPNN 的最大训练次数设为1000，误差精度为0.01，学习速率为0.5。

PSO 算法中粒子的维数根据BPNN 的连接权值和阈值的个数来确定。在此，粒子的维数取N＝41；学习因子c1为粒子对“自身”的认知，学习因子c2为粒子对“社会”的认知，且c1＝c2＝1.49；将PSO 算法中粒子的位置和速度限制在［-0.5，0.5］范围。惯性权重ω 为PSO 算法中粒子继承上一代粒子速度的能力。惯性权重的大小影响着PSO 算法的全局搜索能力和局部搜索能力。为了平衡全局搜索能力和局部搜索能力，采用式（4）对惯性权重进行线性递减：

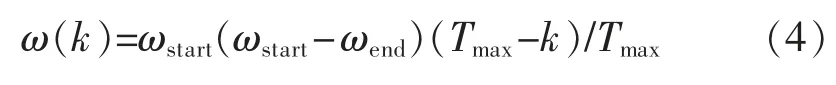
式中：ωstart为初始惯性权重；ωend为迭代至最大次数时的惯性权重；Tmax为最大允许迭代次数；k 为当前迭代次数。初始惯性权重ωstart取较大值可以提高PSO 算法的全局搜索能力，随着迭代次数的增加，粒子位置越来越靠近最优值时将ωend取较小值可以提高PSO 算法的局部搜素能力。故在此取ωstart＝0.9，ωend＝0.4[12]。

3 仿真分析

3.1 BPNN 的仿真

将500 组时延数据分为2 组，取400 组时延数据作为BPNN 的训练样本，100 组时延数据作为BPNN 的测试样本。用BPNN 对400 组训练样本进行训练，若达到误差精度要求则用训练后的BPNN对100 组测试样本进行测试，若测试结果也满足误差精度要求，则用此BPNN 对500 组时延数据进行预测。若不满足误差精度要求则返回继续训练。BPNN 对500 组时延数据进行预测的结果如图3 所示，BPNN 对样本进行训练时训练次数与误差的关系曲线如图4 所示。

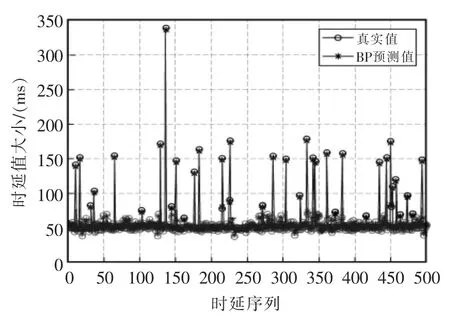
图3 BPNN 对时延的预测Fig.3 Delay prediction by BPNN

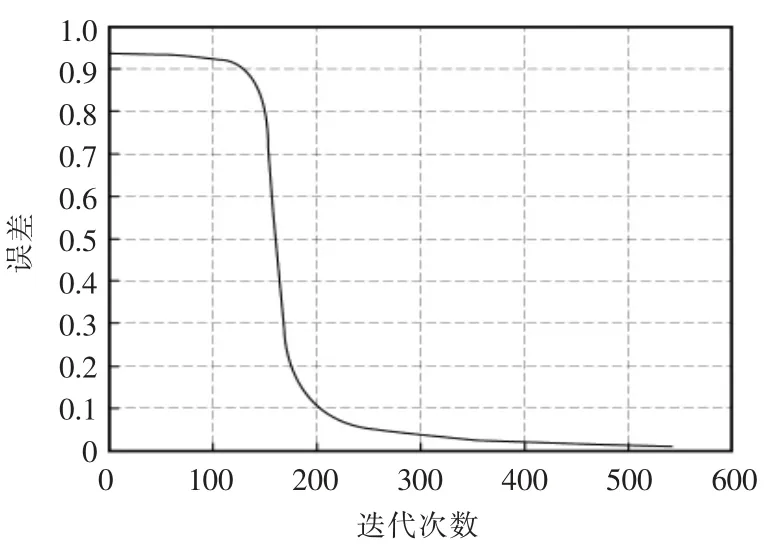
图4 BPNN 训练迭代次数与误差的关系Fig.4 Relationship between training iterations and errors of BPNN

3.2 PSO-BPNN 的仿真

用PSO 优化后的BPNN 对网络时延进行预测，先取测试样本误差平方和为粒子群的适应值函数，用粒子群算法优化求得全局粒子最优的位置即为BPNN 的初始权值和阈值。再用BPNN 对样本数据进行训练，用训练完的BPNN 对500 组数据样本进行预测。PSO-BPNN 对500 组时延数据进行预测的结果如图5 所示，PSO-BPNN 对样本进行训练时训练次数与误差的关系曲线如图6 所示。

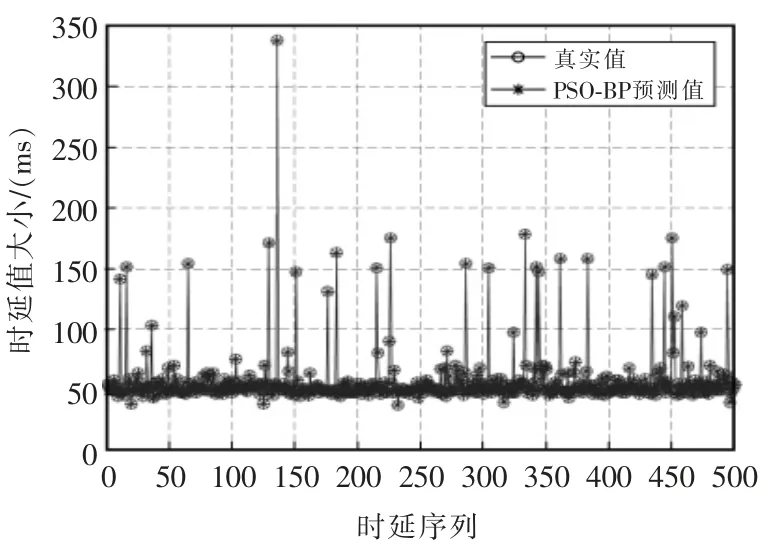
图5 PSO-BPNN 对时延的预测Fig.5 Delay prediction by PSO-BPNN

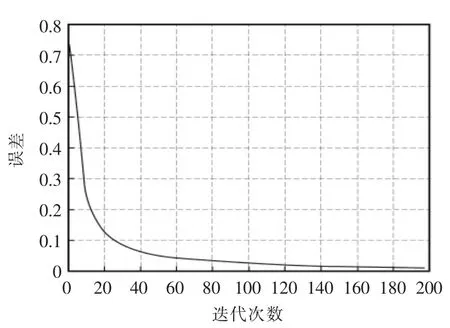
图6 PSO-BPNN 训练迭代次数与误差的关系Fig.6 Relationship between training iterations and errors of PSO-BPNN

3.3 数据的分析对比

为了更直观地表示BPNN 和PSO-BPNN 的训练过程中误差与迭代次数的关系，图4 和图6 中纵坐标误差分别取数据归一化后BPNN，PSO-BPNN的输出值与归一化后的期望输出值差值的绝对值。

对BPNN 时延预测和PSO 优化初始权值，与阈值后的BPNN 时延预测的数据进行对比分析，结果见表1。

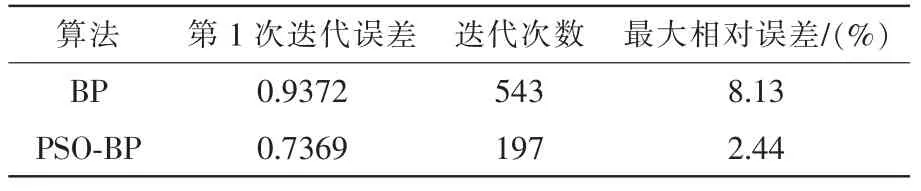
表1 BPNN 与PSO-BPNN 仿真数据比较Tab.1 Comparison of BPNN and PSO-BPNN simulation data

由表1 中第1 次迭代误差的比较，结合图4 与图6，可知利用BPNN 对网络时延进行预测时，初次迭代误差较大，且算法易陷入局部极小值； 利用PSO 对BPNN 的初始权值与阈值进行优化后的BPNN，对网络时延进行预测时，第1 次迭代误差得到了减小，同时避免了算法陷入局部极小值。

由表1 中迭代次数的比较可知，利用BPNN 进行训练，权值和阈值是随机选取的，网络训练了543次后才达到设定的误差精度；利用PSO 优化后的权值与阈值的BPNN，只需要训练197 次就能达到设定的误差精度。说明利用PSO 优化后的权值与阈值的BPNN，比利用随机选取的权值和阈值的BPNN，在达到相同的设定误差精度时迭代次数少，收敛性好。

由表1 中预测值与实际值最大相对误差的比较中可知，PSO 优化的BPNN 对500 组网络时延数据样本的预测，最大相对误差为2.44%，比未优化初始权值和阈值的BPNN 对500 组网络时延数据样本的预测，最大相对误差8.13%要小。说明PSO 优化的BPNN 对网络时延预测的精度要好。

4 结语

为更好地对NCS 随机时延进行预测，采用了PSO-BPNN 算法对时延进行预测。针对BPNN 算法在时延预测中的缺点，在对粒子群算法和BPNN 的理论分析基础上，提出将PSO 算法与BPNN 相结合。利用PSO 算法强大的全局搜索能力，对BPNN的连接权值和阈值初始值进行优化，加快了BPNN的收敛速度，提高了BPNN 的训练效率，同时也避免了BPNN 陷入局部极小值得可能。利用PSOBPNN 算法能够很好地预测网络控制时延，算法迭代次数少，精度更好。