基于转炉干法除尘系统的烟气温度控制策略
田 海,郭林威,闫兆阳,姚震宇
(内蒙古科技大学 信息工程学院,包头014010)
在转炉炼钢过程中,喷枪向熔池通入的氧气与铁水反应,产生大量的热量和烟气,烟气中混入铁和铁的氧化物颗粒及原料中的其它微粒,随意排放转炉烟气会严重污染环境,目前转炉烟气净化主要有干法除尘和湿法除尘两种,相对于湿法除尘,干法除尘具有效率高、 除尘后获得的煤气热值高、系统简化等优点。
实现烟气温度的合理有效控制,不但可以达到较好的除尘效果,而且降温后的烟气进入静电除尘器可保证静电除尘器安全可靠工作[1]。干法除尘系统的有效运行是转炉炼钢正常进行的前提,对稳定工况有重要意义。
转炉烟气温度控制一般采用相关公式法结合PID 调节的控制策略,但因实际烟气流量计算存在误差,造成烟气温度波动较大。为提高烟气控制效果,本文提出一种控制策略:首先用实验建模的方法建立起转炉干法除尘系统中温度的数学模型,然后采用模糊自适应PID 控制方法对烟气温度进行控制,并在Matlab/Simulink 平台下仿真,验证控制效果。
1 干法除尘工艺过程
在转炉氧枪吹氧,与铁水发生反应过程中产生的烟气温度约为1500 ℃,烟气由炉口处的烟罩捕获,经烟罩进入冷却烟道,烟气被冷却到900 ℃左右进入蒸发冷却器,根据烟气的温度控制喷水量,为达到更好的除尘降温效果,在通入冷却水的同时通入蒸汽将冷却水雾化,雾化的水滴经烟气中的热量蒸发,从而起到冷却烟气的作用,精确控制喷水量使蒸发冷却器出口处的烟气温度降到230 ℃~310 ℃。喷射的冷却水和蒸汽也使烟气变得湿润利于烟尘的凝聚,凝聚的大颗粒烟尘受重力下落,再经粗灰输送机构输出,此时烟气中30%~50%的烟尘被除去。下一步烟气进入圆筒形静电除尘器,除尘器首先对烟尘充分荷电,荷电后的烟尘在电场力作用下到达阳极板,然后被振打器敲落再由刮灰机刮落,通过细灰输送机构输出,经过电除尘器的烟气,其烟尘含量低于10 mg/m3。除尘后的烟气进入到切换站,若烟气符合回收条件,其在煤气冷却器进行冷却后送至煤气柜储存,若不符合回收条件则通过放散烟囱点火放散,其工艺流程如图1 所示。
经蒸发冷却器处理的烟气温度要求控制在200 ℃~300 ℃,若烟气温度过低,进入静电除尘器的潮湿烟尘易粘结在一起附在阴极线上,导致阴极线肥大,使除尘电场放电频繁,严重腐蚀电场内设备;若烟气温度过高,烟尘的电阻率升高,静电除尘器的工作效率下降,导致排放的烟气含尘量增多。
为稳定蒸发冷却器出口处的烟气温度,除加强设备维护管理外,还需要优化工艺,在影响烟气温度的诸多因素中,冷却水流量的控制最为重要,因此准确控制冷却水的流量是稳定蒸发冷却器出口烟气温度的关键。
2 烟气温度控制系统建模
为了便于研究蒸发冷却器对烟气温度的控制情况,确定控制参数,需要建立相关数学模型。
2.1 温度模型的建立
在影响烟气温度的各种控制量中,喷水量是最主要的因素,为研究方便,建立以喷水阀门开度为输入量,经蒸发冷却器处理的烟气温度为输出量的数学模型。若直接采用连续模型辨识,模型拟合效果较差,故先选择离散模型进行辨识,再将离散模型连续化,转换为连续模型[2]。应用机理模型和测试建模相结合的方式,先通过机理得出系统的模型类,然后将测试建模得到的高阶离散传递函数转换为连续模型再化归为所需的机理模型类,这样得到的模型既保证了一定的精确度,又简化了模型结构,便于控制。
2.1.1 机理模型
蒸发冷却器出口烟气温度采用相关文献中由机理分析获得的模型[3]:
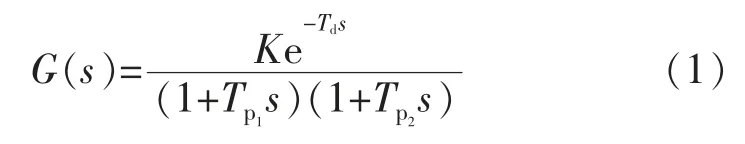
式中:G(s)为建立的系统模型;K 为冷却水阀门开度的增益;Td为冷却水阀门开度的纯滞后时间;Tp1为冷却水阀门的时间常数;Tp2为蒸发冷却器入口烟气流动速度的时间常数。
2.1.2 辨识模型的建立
系统辨识参数有多种方法,其中最小二乘法可以在最小方差意义上得到一个与实验数据拟合度最高的数学模型,所得到的结果具有无偏性、有效性、一致性。采用Matlab R2016b 中的系统辨识工具箱进行辨识,该工具箱辨识算法采用最小二乘法。图2 为系统辨识工具箱主页面及各种处理数据,在Matlab R2016b 主命令窗口中输入“ident”便可以直接进入工具箱主页面,对转炉干法除尘系统进行系统建模的详细过程如下:
辨识数据的准备辨识对象的输入数据为某炼钢厂转炉的喷水阀门开度,其范围为0~100;输出数据为蒸发冷却器出口的烟气温度,温度范围为230 ℃~300 ℃,辨识数据一共150 组(数据来源于参考文献[3]中的附录)。
数据导入从现场采集到的数据,首先将奇异数据剔除,然后把数据导入到Matlab 工作窗口,在系统辨识工具箱的Import data 下拉列表中导入工作窗口中的数据,数据名为“mydata”,采样时间为2 s。
对数据预处理工具箱主窗口Preprocess 下有多种预处理方式,选择对辨识结果影响较大的去除趋势预处理方式,消除数据中的大畸变。处理后的数据名称为“mydatad”。将预处理过的150 组数据分为2 组,第一组名为“mydatade”,共90 组,用于辨识参数;第二组名为“mydatedv”,共60 组,用于对辨识数据的验证。

图2 系统辨识工具箱主窗口Fig.2 Main window of the system identification toolbox
2.1.3 模型验证拟合
图3 即为各模型的拟合度,单击工具箱主窗口Estimate 下拉列表,选择Polynomial 模型,对非线性系统选择其中的ARX 模型,通过设置不同的ARX模型参数可在系统辨识工具箱主页面得到不同模型,单击Model output,便可得到各模型的拟合度。
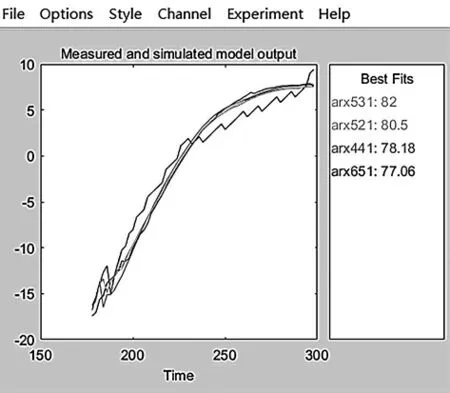
图3 各模型拟合度Fig.3 Fitting degree of each model
2.2 离散模型连续化与降阶处理
拟合度最高的离散模型传递函数如式(2)所示,在Matlab 中用函数d2c,将其转换到s 域上,得到连续的传递函数如式(3)。式(3)得到的模型阶次较高,参考前文的机理模型,将其进行降阶处理,采用带有时间延迟的次最优降阶算法,降阶处理后,得到新的控制模型如式(4)所示。

式中:G1(z)为离散系统传递函数模型。
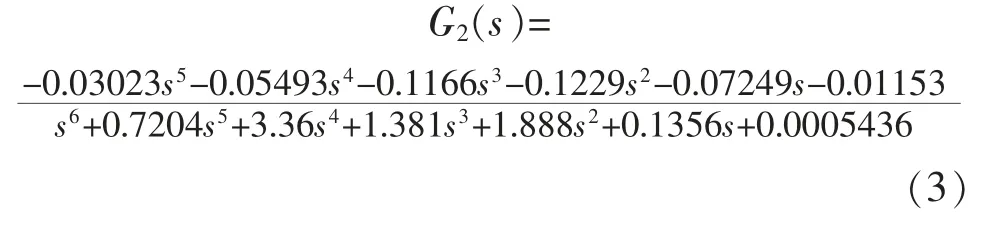
式中:G2(s)为离散系统传递函数连续化的连续系统函数模型。
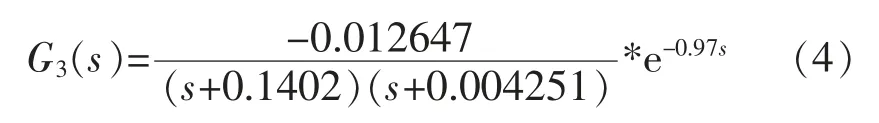
式中:G3(s)为降阶后得到的最终传递函数模型。
为检验降阶模型的准确性,对原模型和降阶模型做单位阶跃响应和伯德图曲线,分别如图4、图5所示,可见采用带有时间延迟的次最优降阶算法得到的降阶模型可以很好地逼近原模型。
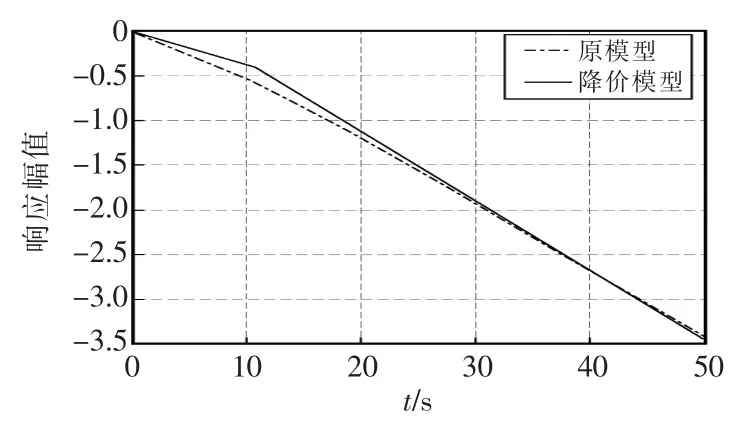
图4 原模型和降阶模型的阶跃响应曲线Fig.4 Step response curves of original model and reduced order model

图5 原模型和降阶模型的伯德图Fig.5 Bode diagram of original model and reduced order model
3 烟气温度控制算法
控制蒸发冷却器出口的烟气温度在符合要求的范围内,需采用合理的控制方式对蒸发冷却器喷射的冷却水流量和蒸汽流量进行控制。
3.1 控制策略
在转炉吹炼阶段,烟气流量和温度相对平稳,蒸汽流量可取固定值,只考虑对烟气温度影响较大的冷却水流量的控制[1,4]。传统的PID 控制其控制参数无法在线整定,烟气温度调节不稳定,对后续除尘工序不利。为提高控制效果引入模糊自适应PID控制方式,模糊自适应PID 可根据烟气温度设定值和实际值的偏差及偏差变化率自动调整控制参数,有效抑制烟气流量变化等因素对温度调节的干扰,具有更好的控制性能。
3.2 模糊自适应PID 控制器的构造
模糊自适应PID 控制器由模糊控制器和PID控制器组合而成,模糊设计可分为如下步骤:
(1)输入输出量的选择及其模糊化;
(2)输入输出量的隶属度函数选择;
(3)模糊控制规则表的建立;
(4)依据模糊规则表进行模糊推理;
(5)模糊量的清晰化。
公式(5)为系统的控制参数,其中PID 控制器的参数为比例系数kp0、积分系数ki0、微分系数kd0,在本设计中,经过整定三个系数分别取-1.35、-0.0041、-5。模糊控制器的输出量为比例、积分、微分系数的变化参量Δkp、Δki、Δkd,通过对PID 控制器的参数进行实时修正,由修正后的比例、积分、微分系数kp、ki、kd去控制执行机构,图6 为控制器的结构框图。

图6 模糊自适应PID 框图Fig.6 Fuzzy adaptive PID block diagram

3.2.1 输入输出语言变量的确定
模糊控制器以烟气温度的实际值和设定值的差值及差值变化率作为输入值,基本论域分别取[-13 5]、[-20 6],定义输入语言变量“误差E”、“误差变化率EC”作为各自的模糊量;输出量为比例、积分、微分系数的增量Δkp、Δki、Δkd,基本论域分别为[-3 0]、[-0.004 0]、[-18 -12],定义输出语言变量ΔKp、ΔKi、ΔKd作为各自的模糊量,输入输出模糊量的论域均设置为离散整数论域[-3,-2,-1,0,1,2,3],两输入量的量化因子分别取0.33、0.23,三个输出量的比例因子分别取0.5、0.00067、1。各语言变量语言值均设置为7 档,即{NB 负大,NM 负中,NS负小,Z 零,PS 正小,PM 正中,PB 正大}。输入语言变量的隶属度函数选用高斯型,输出语言变量隶属度函数选用三角型。
3.2.2 模糊规则库的确定
可根据控制过程的模糊模型,即通过模糊语言来表述被控过程中的输入、输出量关系,得出控制规则。比例系数可提高系统响应速度,但若过大,会产生大的超调;积分系数可消除稳态误差,但过大会引起积分过饱和; 微分系数可减小系统超调,但过大会增加系统的调节时间。可根据三者对系统响应的影响综合考虑建立控制规则[5-6]:
(1)若系统存在较大的偏差,需加快响应速度,可加大Kp的取值,Kd取较小值,以避免偏差快速变化出现微分过饱和,Ki取0 或取小值来减小超调引起的积分饱和;
(2)当偏差和偏差变化率大小适中时,为减小超调可使Ki取值适中,Kp取较小的值,同时Kd亦取适中值;
(3)偏差值较小时,Kp,Ki的取值大一些以维持稳态性能,此外当偏差变化率较小时,Kd取值大一些,偏差变化率较大时,Kd取值小一些。
根据上述的控制原则和PID 参数整定情况,可得到模糊控制规则表如表1 所示。
3.2.3 模糊量的清晰化
由模糊推理得到的模糊输出是模糊子集,需将其转换为模糊控制器的精确输出量ΔKp、ΔKi、ΔKd,本文采用重心法求取ΔKp、ΔKi、ΔKd,即对模糊输出量各元素和对应的隶属度函数μ 求加权平均值,以求取ΔKp为例,如下式所示:

表1 ΔKp、ΔKi、ΔKd 相应的模糊控制规则Tab.1 Fuzzy control adjustment rules corresponding to ΔKp、ΔKi、ΔKd

再将ΔKp、ΔKi、ΔKd转换为实际作用参数[7]Δkp、Δki、Δkd,以求取Δkp为例,如公式(7)所示:

式中:Kkp为Δkp对应的比例因子,Δkpmax和Δkpmin分别为Δkp所取基本论域的上下限。
3.3 仿真结果及其分析
在Matlab/Simulink 中搭建框图进行仿真,温度设定值取250 ℃,温度响应曲线如图7 所示。
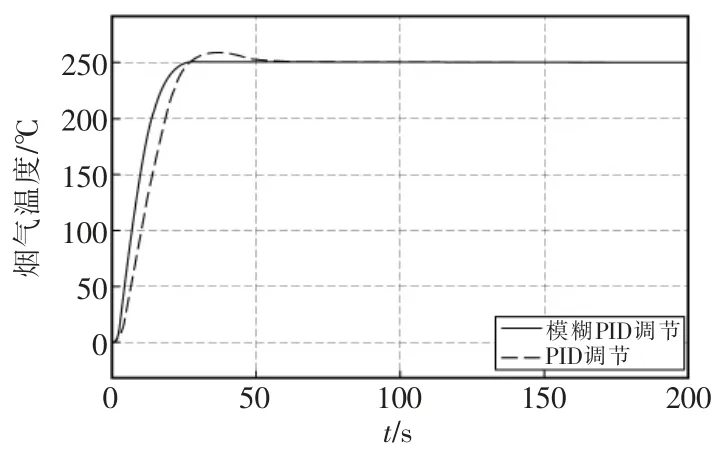
图7 PID 控制和模糊PID 控制烟气温度仿真曲线Fig.7 Simulation curve of flue gas temperature controlled by PID control and fuzzy PID control
由图可见,采用模糊自适应PID 控制,在PID调节效果的基础上加快了系统响应速度,且几乎不产生超调。该控制系统实现了PID 参数的动态整定,优化了系统控制性能。
4 结语
本文针对转炉干法除尘烟气温度的控制要求,对转炉干法除尘烟气温度控制系统进行了深入研究,辨识出了系统的传递函数,采用模糊自适应PID控制方式进行控制调节,并在Matlab/Simulink 下进行了仿真对比,仿真结果显示应用此控制策略,加快了系统响应速度且几乎消除了超调量。本文仅就主要因素喷水流量对烟气温度影响展开讨论,为达到更好的烟气处理效果,还需对影响烟气温度的其他因素做进一步研究。

