基于深度学习的电力设备智能运行方式的研究

虞 跃

（国网冀北电力有限公司秦皇岛供电公司，秦皇岛066000）

在电力市场下，随着电网技术日益迅速地发展和应用，其网络拓扑结构变得愈加错综复杂、交织多变，设置在智能电网中的电力设备在运行过程中往往受到电网运行环境的各种影响，比如电网中谐波、磁场、温度、湿度、纹波、杂波信息干扰等因素，导致电力设备偏离工作标准，严重时，甚至发生意外事故。电网维护工作人员往往在观察到设备无法正常运行，或者出现故障后才获得电力设备的情况。在电力设备正常运行过程中，很难通过运行数据、宏观的数据特征获取更为本质的信息。这就使隐藏在宏观数据的信息特征无法被挖掘出来，电力设备在工作过程中将存在诸多隐患，影响电力市场的健康、稳定、安全发展[1]。故在此以深度学习为基础，融入新发展的人工智能技术，将电力设备的运行、监控、维护等紧密结合在一起，通过日常运行数据，挖掘、训练、学习各个数据之间的关系，及时排除运行风险，并实现故障的快速发现和处理[2]。

1 智能运行方式体系架构设计

研究中所构建的新型智能运行方式体系架构如图1 所示，包括设备层、数据采集层、深度学习层、计算机管理层和应用层。

图1 智能运行方式体系架构Fig.1 Architecture of intelligent operation mode

智能电网以及设置在其内的电力设备、传感器均属于设备层。数据采集层采集电力设备运行的各种数据，这些数据信息包括电力电路网络故障、变压器故障、电源供电故障、母线故障等信息。电力信息多样，还存在导致电力设备故障或者无法正常运行的电网数据集合，如：电网中出现的同频、异频信号，电力设备运行中出现的电流无功功率、电压无功功率、杂散波谐波信息、异常电压、谐波电流、电压不平衡值、电流不平衡值、电压/电流闪变/瞬变、电网杂波干扰、振动、温湿度、谐波干扰、异常事件等多项指标。这些数据大都比较分散，数据之间的规律难以掌控[3]。

在深度学习层，已有多种方式的深度学习算法，较常见的深度学习模型与架构包括CNN，DBN，RNN，RNTN，GAN，以及自动编码器、大数据挖掘算法模型，比如K-Means 算法模型、支持向量机模型、Apriori 算法模型、最大期望（EM）算法模型、Adaboost 迭代算法模型、关联算法模型、故障诊断模型、随机矩阵算法模型等多种计算模型。这些算法的一个共同特点，就是能够将采集到的宏观数据转换为直观识别的信息数据，用户通过将宏观数据输入至相关的大数据分析模型，能够得出相应的数据管理，从而有利于用户管理、监控或维护电力设备。在此，仅阐述有代表性的深度学习算法，由此体现研究的技术特征[4]。

2 深度学习算法模型

2.1 故障诊断模型

对电力设备运行情况的监督往往采用故障诊断模型，传统人工方法的诊断能力就显得非常有限。在此采用了BP 神经网络算法模型（back-propagation network），能够对采集到的电力设备故障信号进一步地进行映射、处理，有效地处理电力设备较为复杂的故障信息非线性关系，并通过数学模型表现出来[5]。该模型如图2 所示。

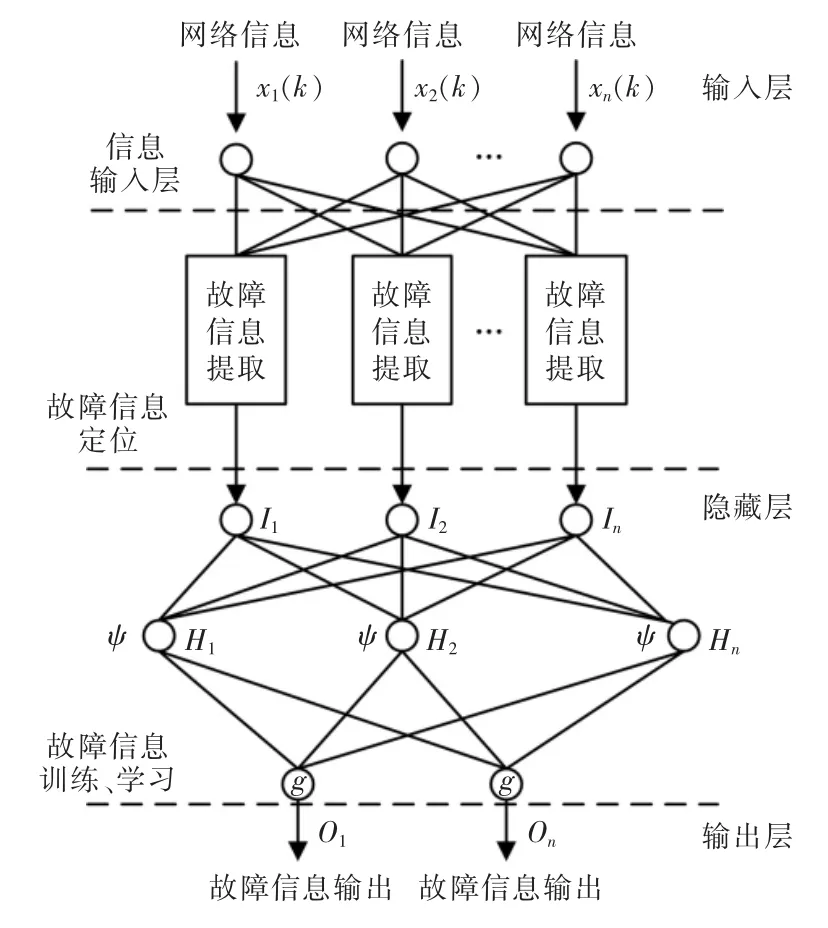
图2 BP 神经网络算法模型Fig.2 BP neural network algorithm model

由图可见，该算法模型包含了输入层（可以作为电网信息输入层）、蕴含层（可以作为故障信息定位层）、输出层（可以作为故障信息训练、学习层）。通过信息输入层输入上述影响电力设备的多种类型故障数据信息。为达到一定的调节效果，通常设置不同的权值或者阈值，能够逐步逼近BP 神经网络算法模型输出的结果，从而提高训练精度，减少计算误差。

在此介绍应用上述计算模型所引入的公式。要使BP 神经网络算法模型能够正常运行，需要调整其输出层权系数，即

式中：Δωki为BP 神经网络算法模型的输出层权系数；为BP 神经网络算法模型的的信息期望输出值；为BP 神经网络算法模型进行计算的输出；η为常数。

同时，也需要对BP 神经网络算法模型的隐含层权系数进行调整，即

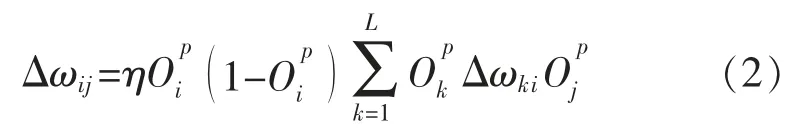
在采集到的大量电力设备故障数据信息库中，由于数据信息形式不一，如图片、文本、声音、音频等，信息特征是非线性较强。如果每种数据形式采用一种方式，就会出现多种计算模型，计算起来极为不便[6]。故在此采用二次型准确函数模型，即

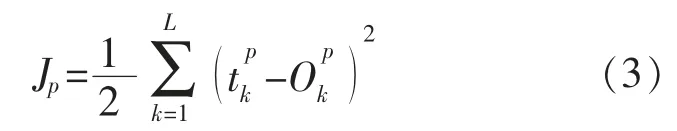
对于N 个电力网络中的故障设备信息样本，总准确函数为

在评价电网信号中电力设备故障类型信息时，为进一步提高学习精度，需要对接收到的数据进行标准化处理。比如，在输入层输入电力设备故障信息时，假设有m 种不同的故障类型（如变压器故障、电源供电故障、母线故障等），这些数据共有N 种，对输入的故障数据xij实施标准化处理的公式[7]为

其中

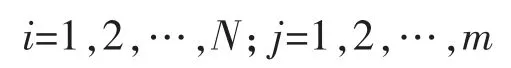
为适应多种情况下的计算，对Zij进行标准化计算，即

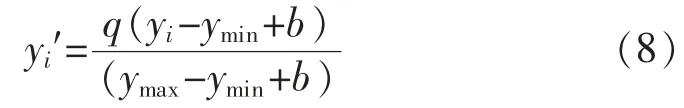
式中：yi为输出电力设备运行故障数据样本；yi′为标准化后的电力设备运行故障数据样本信息；ymax为输出电力设备运行故障信息数据样本中的极大值；ymin为输出电力设备运行故障信息数据样本中的极小值。

在式（1）～式（8）的应用过程中，数据输出的精度情况取决于网络的层数、 隐层神经元的个数、初始权值（一般选择（-2，2））的选取，以及学习速率（一般选择0.02～0.7）和期望误差的选取。利用上述参数则可以构建BP 神经网络数学模型[8]，进而实现多种运算。

2.2 数据关联模型

随机矩阵理论数学模型在处理复杂配电网系统输出的能谱和本征态具有突出的优势，通过构建出的数学模型揭示宏观数据中整体关联的行为微观特征，有利于把握更为本质的数据信息。

矩阵模型为

其中

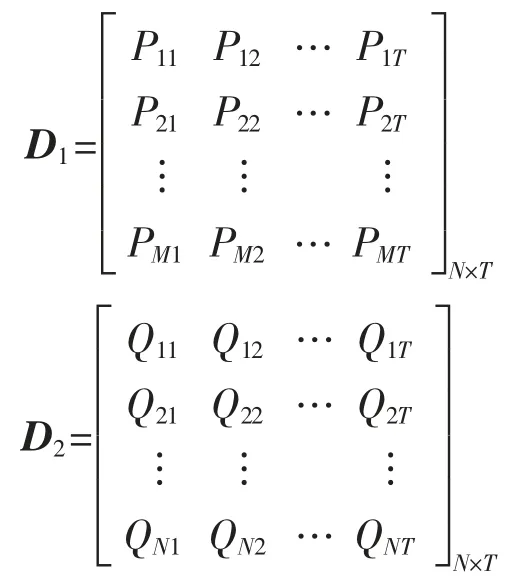
式（9）表示D1与D2在（M+N）×T 下的关联性。式中：T 为获取数据样本的测量次数；M 为假设待研究的电力设备运行的数据类型数，该M 种数据用数据集合记为｛P1，P2，P3，…，PM｝；D2为电力设备在运行过程中产生的数据类型，如电流、电压、功率、负荷等，此类数据以集合的形式记为｛Q1，Q2，Q3，…，QN｝；N 为电力设备在运行过程中产生的数据种类。

假设，n 个电能数据变量构成的向量集合为

数据变量的量测数据可以构成一个列向量，按时间顺序对所测的电力设备数据进行排序，可得矩阵为

式中：Ω 为电力设备产生数据的数据库；ω1，ω2，…，ωM+N分别为矩阵D1和D2中单个元素的集合[9]；Dstd的值表示数据集合D1与数据集合D2间的关联性。

2.3 数据分类算法

在一种深度学习算法中，采用决策树算法，再以ID3（iterative dichotomiser 3）算法作为示例加以说明。对数据分类时，要先设计出分类器，分类器在数据样本中经过学习、训练可以自动生成。其模型如图3 所示。

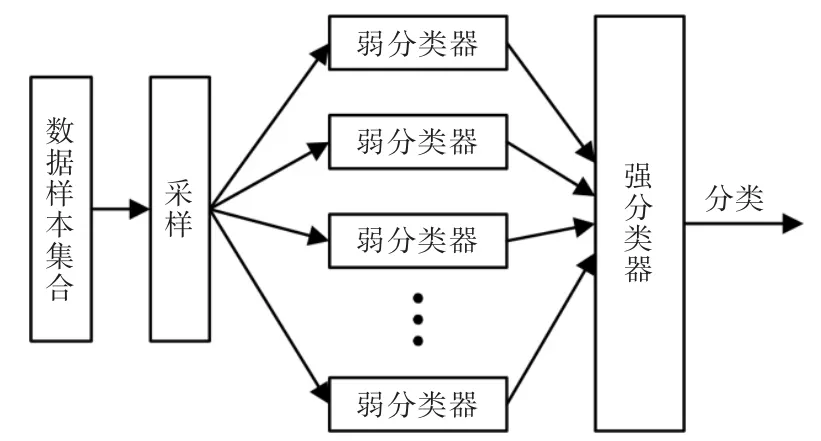
图3 分类器训练Fig.3 Classifier training

利用强分类器能够提高数据输出的精确度，在属性分类上显得更加强悍。确定了分类器以后，就要确定分类器的节点情况。节点分为算法模型的总节点和分支节点，先确定总节点再构建分支节点，这样就可以构建决策树模型[10]。所需的一个数据参数——经验熵H（D）为

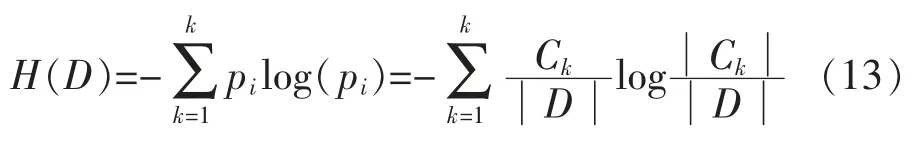
经验条件熵H（D/A）为选择的数据样本的特征A 在数据集D 中的信息增益，有

由式（13）（14），可以计算出分类数学模型中决策树的根节点。然后，将信息增益度值较大的属性（作为根节点设置）设置在决策树的顶层，次之的信息增益度值放置在根节点的下端，最后将最小的信息增益度值的属性作为决策树算法模型中的分支节点。在确定好根节点和分支节点的属性以后，就建立起分类模型。

3 试验结果及分析

对以上深度学习的效果验证，由于篇幅所限，在此仅对BP 神经网络算法模型、 随机矩阵理论数学模型和决策树算法进行验证，通过代表性示例说明深度学习算法在电力设备智能运行方式中的效果。

3.1 试验环境

硬件——计算机系统；

软件的操作系统——Windows 2015；

应用软件——C#，Tensorflow，Python，NumPy，SciPy，iPython，等。

3.2 试验方法

验证试验在合肥学院人工智能与大数据学院实验室计算机机房内进行，选用1 台计算机，调取数据库信息，对收集到的数据信息清洗、过滤，其组件如图4 所示。采用不同的数学模型进行试验，通过计算机进行仿真、计算。

图4 试验架构模型Fig.4 Experimental architecture model

3.3 试验分析

3.3.1 BP 神经网络模型仿真验证

对BP 神经网络算法模型仿真验证时，启动MatLab软件环境，随机从数据库中调取电力设备运行效率，然后进行智能仿真。仿真过程中采用以下公式：

准确率计算公式为

召回率计算公式为

最终得出FI 值：

在进行数据验证时，分别选择电压、电流、纹波、负荷、谐波等数据信息5×104个，得出的数据样本见表1。得到的仿真曲线如图5 所示。

表1 BP 神经网络模型试验数据Tab.1 Test data of BP neural network model

图5 BP 神经网络模型仿真试验Fig.5 Simulation test of BP neural network model

由表可知，在测量时间20 s 内，利用BP 神经网络模型计算后的结果，反应时间为6.5，7.2，6.3，7.1，7.5 s，获得相应的召回率和正确率，误差比较小。

3.3.2 随机矩阵算法验证

试验时假设矩阵D1为80×150，D2为400×500，然后根据式（12）求值。随机矩阵算法验证试验数据见表2。

表2 随机矩阵算法试验数据Tab.2 Test data of random matrix algorithm

将表2 数据代入式（9），可得

最后可得表2 中的Dstd计算值。可以用曲线图来表示不同参数之间的相关性，如图6 所示。

图6 随机矩阵算法仿真试验Fig.6 Simulation test of random matrix algorithm

图中，Dstd值表明电力设备输出的电流、电压、功率等参数与电网中存在的干扰信息（磁场、谐波和负荷）有着密切的关系：Dstd值越大，磁场、谐波和负荷等干扰因素影响程度就越大。由图可见在电力设备运行过程中磁场、谐波和负荷与电力设备运行数据之间所存在的关系。

3.3.3 分类算法验证

假设该算法模型输出数据特征A1，A2，A3，A4，A5对数据集合D 的信息增益，样本库见表3。

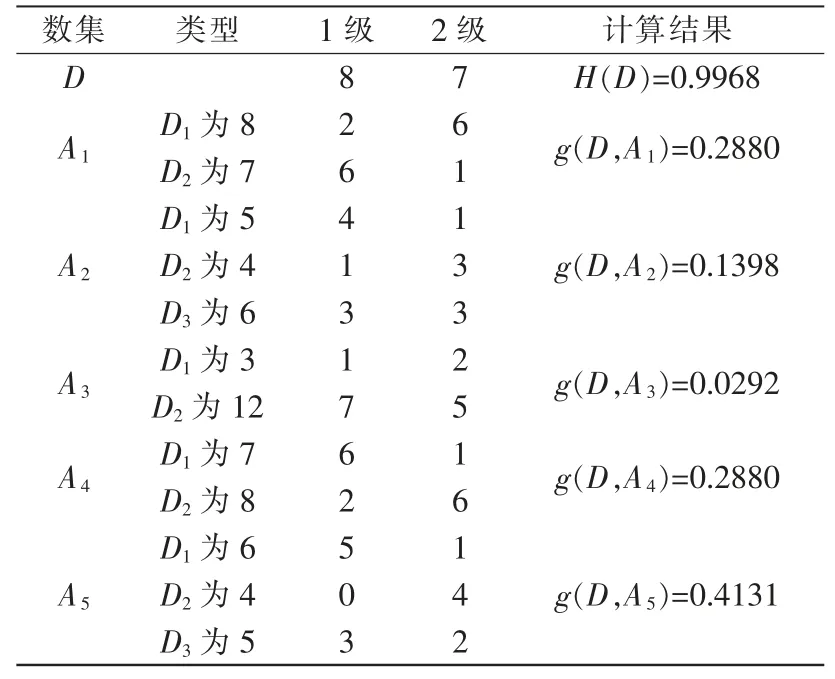
表3 数据库样本库Tab.3 Database sample library

根据式（13）（14）求值，可得

结果可得出，A5的信息增益为最大。然后选择A5为根节点，针对A5再进一步划分，可得

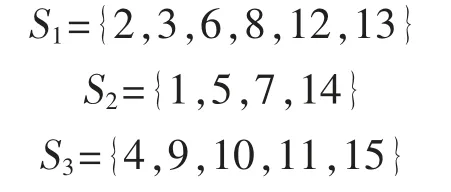
将这些数据集合划分为子节点，直至输出用户满意的数据为止，一种示例性划分如图7 所示。

图7 决策树示意图Fig.7 Diagrammatic sketch of decision tree

通过这种数据模型，能够使用户快速从电力设备数据库中查到谐波干扰数据，大大提高了数据检索的效率，增强了大数据的分类能力。

4 结语

通过研究将各种深度学习算法应用到电力市场中，提高了数据的运算能力，可以使用户快速获取、计算、分析电力网数据，解决了目前手工安排运行方式工作量大、效率低的问题。然而仍存在一系列问题，如：数学计算的精度有待考究，且需要充足的数学理论来支撑，虽然在一些理论上可行，但是在具体应用过程中，可能存在计算模型滞后等现象；深度学习在建模时，需对大量的数据反复计算以总结出算法模型的经验值，如果数据量不够大则可能影响精度；多种深度算法配合使用时，容易出现数据交叉感染现象，数据存在串出的情况，为此尚需要反复训练，以总结运行经验。