基于区域分割的多视角点云精简算法
梁正友,黄思捷,孙 宇,李轩昂
(1.广西大学 计算机与电子信息学院,广西 南宁 530004;2.广西多媒体通信与网络技术重点实验室,广西 南宁 530004)
0 引 言
由于微软推出的体感设备Kinect V2在三维重建领域当中的点云信息采集上表现出操作简单、易上手、价格廉价等优点[1],受到了许多研究者的关注。Kinect V2获取点云的数量非常庞大,平均每秒能够获取数以千计的点。这些点云不仅密度大,而且包含了许多重复点和冗余点。如果不对点云进行精简,这些多余的点云会占用大量的存储空间,直接进行曲面重建必定会浪费大量时间和计算资源[2]。因此,研究开发有效的点云精简算法可有效地减少点云占用存储空间,提高运算效率。
已经有不少学者研究开发各种点云精简算法。唐泽宇等[3]提出一种基于加权最小二乘法曲率计算的点云精简算法,能够有效提升曲率计算的准确度,避免了孔洞现象。金露等[4]在利用自适应栅格法对点云进行精简的基础上,将ICP算法和RANSAC算法相结合,同时提高了点云配准精度和精简的效率。贺一波等[5]提出了一种基于k均值(k-means)聚类的点云精简方法,能较好地保留点云的细节特征,并且与原始数据的稠密稀疏分布更加一致。曹爽等[6]针对工业构件点云提出了基于曲面变化的点云精简算法,通过计算点的曲率将点云分成特征不同的多个区域,并且在每一个区域设定阈值,为每个不同的特征区域计算其精简比率,由精简比率定义阈值完成精简。陈达枭等人[7]利用包围盒子把点云划分成若干个子空间,利用每个子空间获取K邻域点集的拟合平面,根据拟合平面距离,把每个子空间分为保留区和删除区,最后根据精简率对删除区内的点云进行精简。Nallig Leal等[8]提出了一种基于点云局部密度估计的点云精简方法,使用期望最大化算法对点云密度分布进行聚类,识别高曲率点作为非去除的点,最后采用线性规划对去除点进行精简。Yuan Xiaocui等[9]采用K均值聚类算法对点云进行全局聚类,随后利用K-d树的节点作为初始聚类中心,并且使聚类中心映射到高斯球,最后利用自适应均值漂移算法对高斯球中的数据进行精简;Han Huiyan等[10]利用边缘点比非边缘点具有更强的几何特征,区分边缘点和非边缘点并且保留边缘点,对于非边缘点利用欧几里得距离的平均值来判定该点是否需要去除,来完成点云精简。Whelan T等[11]提出了一种渐开线点云图的增量平面分割方法和一种有效的平面曲面三角剖析方法来进行点云的精简;Qi Junkun等[12]利用图的光谱处理,判别出点云上不规则的点,提出基于图滤波器点云精简公式,对不规则的点进行精简;Xuan Wei等[13]提出了一种简化点云的新方法,该方法使用基于法向角的局部熵来评价该点是否为除去对象。Ji Chunyang等[14]提出一种细节特征点简化算法。该算法设置k邻域搜索规则以确保找到的点最接近样本要点,对测量点的进行重要性评估,然后使用八叉树结构来简化剩余的点。该方法不仅可以简化点云,同时对简化目标点云的窄轮廓也有很好的效果。Li Haoyong等[15]提出了一种基于法向量标准差的点云快速简化算法。该算法对下采样后的稠密点云数据计算正态分布,通过相邻点之间的法向夹角计算特征点与另一特征点之间的分离阈值,在特征点与其他特征点之间再逐步进行下采样,实现点云的自适应简化。该算法在短时间内实现了点云模型的有效简化,很好地保持了原模型的特点和形状。
尽管目前点云精简算法研究取得了非常好的进展,但还有较大的提升空间。在对一个建模物体进行多视角采集点云的场景下,由于不同视角的两个相邻点云拥有局部重叠区域,在配准之后,使得重叠区域点云密度过大,出现占用过多的存储空间和降低计算机效率等问题。针对这些问题,该文提出一种多视角点云精简算法,对拥有局部重叠区域的多视角点云序列,使用包围盒子提取两个相邻点云的重叠区域内的点云,将它们分割成重叠区域点云和非重叠区域点云。随后提出一个分组随机精简算法对重叠区域内的点云进行精简。对所有的重叠区域点云精简之后,与非重叠区域点云再合并成一个整体点云,根据精简率的要求在对整体点云进行一次精简。对提出的精简算法和基于包围盒子精简算法[16]进行实验对比,分别使用基于包围盒子的精简算法和该文提出的精简算法对原始点云在75%、50%、25%精简率的实验条件下进行对比。实验结果表明,在相同的精简率下,与基于包围盒子的精简算法相比,该文提出的点云精简算法更能减少对目标物体点云细节的破坏,最大程度上保留目标物体的点云细节和特征。
1 提出的精简算法
本节包括三个小节。第1.1节介绍基于包围盒子的重叠区域内点云提取方法,用于将多视角点云分割成重叠区域和非重叠区域,以便对密度不同的区域进行不同的精简。第1.2节提出一种基于分组的点云随机精简算法,对点云按一定的规则进行排序,然后按等点数量进行均匀分组,对每个分组精简同样数量的点。该算法能克服信息精简分布不一致的问题,较好地保留点云的细节。第1.3节提出多视角点云精简算法,使用包围盒子重叠区域内点云提取方法将多视角点云分割成重叠区域点云和非重叠区域点云。随后用分组随机精简算法对重叠区域内的点云进行精简。对所有的重叠区域点云精简之后,与非重叠区域点云再合并成一个整体点云,根据精简率的要求再对整体点云进行一次精简。
1.1 基于包围盒子的重叠区域点云的提取
对有局部重叠区域的两个点云A和B,如图1所示,左边矩形是点云A的包围盒子,右边矩形是点云B的包围盒子,两矩形相交形成的小矩形是点云A和点云B的重叠部分。
重叠区域点云提取算法步骤如下:
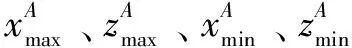
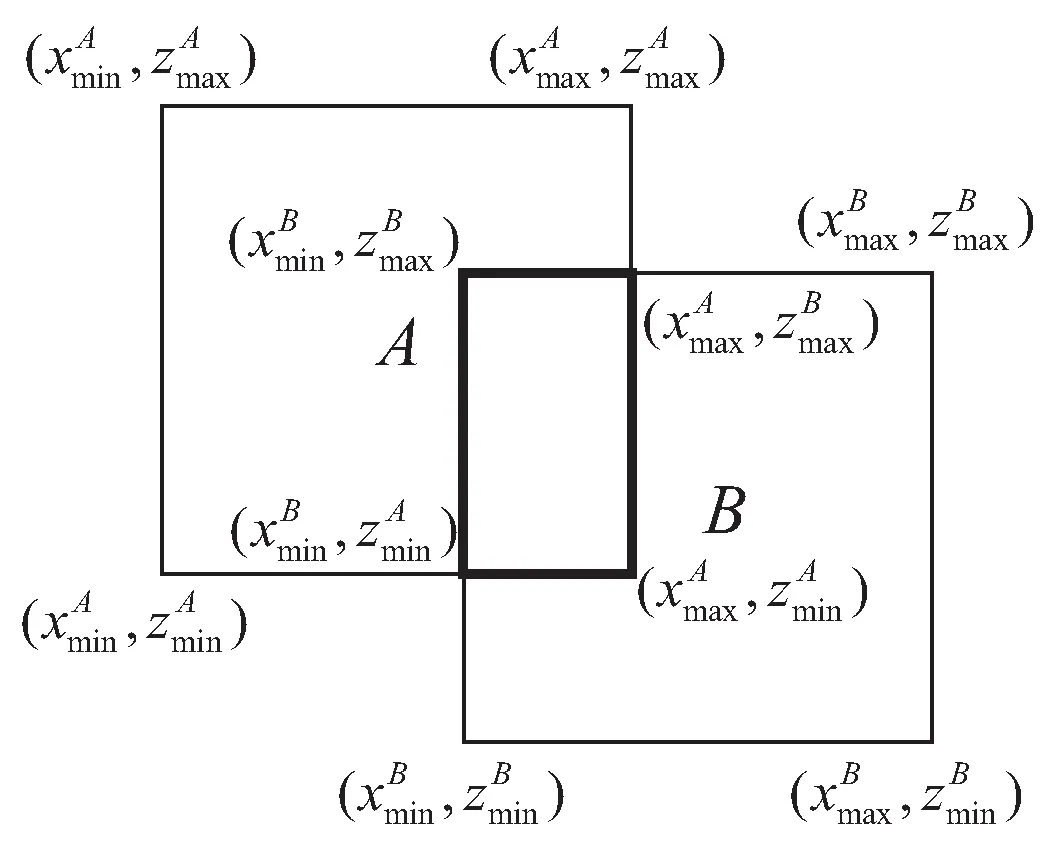
图1 重复区域点云提取

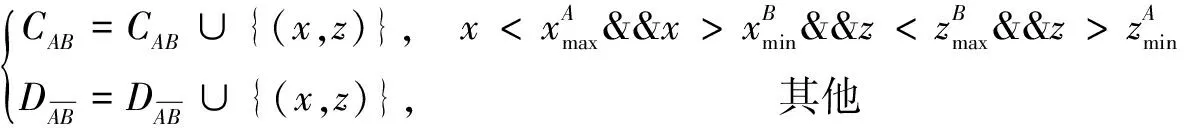
(1)

1.2 基于分组随机精简法
基于包围盒子的精简算法[14]是一种均匀的精简方法,它将点云空间均匀划分成等大小的子包围盒子,每个子包围盒子仅保留一个中心点并去除子包围盒子领域内的其他点。但是,Kinect V2采集到建模物体的点云并不是均匀分布在空间内的,有些区域的点非常稠密,而有些区域的点比较稀疏。因此,使用包围盒子点云精简算法会把点云空间均匀划分成等大小的子包围盒子,这会导致在每个区域内的点数量分布不一致,点会大量集中在某几个子包围盒子内,其他子包围盒子只有少量点甚至没有点;造成有些地方精简过多,有些地方精简过少,使得精简效果不好。针对这些缺点,该文提出了基于分组随机精简算法。首先,对点云按一定的规则进行排序,然后按等点数量进行均匀分组,对每个分组精简同样数量的点。该算法能克服信息精简分布不一致的问题,较好地保留点云的细节,具体描述如下。
在Kinect V2的世界坐标中,建模对象的宽度维度为x轴,深度维度为z轴,高度维度为y轴。为保留建模对象的细节,采用在y轴上的点以y坐标值从高到低排序的方式,让无序点云变成有序点云。
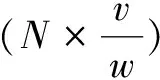
由于是均匀分组,保证每一组点云精简的数量是一定的。合适大小的分组能确保在随机去除点的情况下,不会造成在某一区域过度精简而导致空洞的出现,能最大程度地保留建模对象的点云细节和特征。
1.3 多视角点云精简算法流程
对有局部重叠区域的多视角点云,重叠区域是稠密区域,而非重叠区域是稀疏区域。为了使得这些稠密区域被精简多一点,稀疏区域被精简少一点,首先对重叠区域进行一次精简,然后对包括重叠区域在内的整体点云再精简一次。每次精简的程度用精简率进行衡量。设原始点云D包含点数量为N,经过精简后得到的点云Dl包。Dl含的点数量为M,则精简率r定义为:
(2)
对有局部重叠区域的多视角点云精简的总体思路是:对0°到180°内的多视角点云配准后,对两个邻接点云用1.1节方法提取重叠区域。然后,用1.2节提出的精简方法对重叠区域进行精简。得到的新点云在和邻接的点云继续采用1.1节方法提取重复区,并用1.2节提出的精简方法对重复区域进行精简。重复直到所有的重叠区域都被精简了。然后对整体点云再进行一次精简,以达到要求的精简率。形式化描述如下:
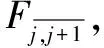
/*多视角点云精简算法*/
BEGIN
步骤一:
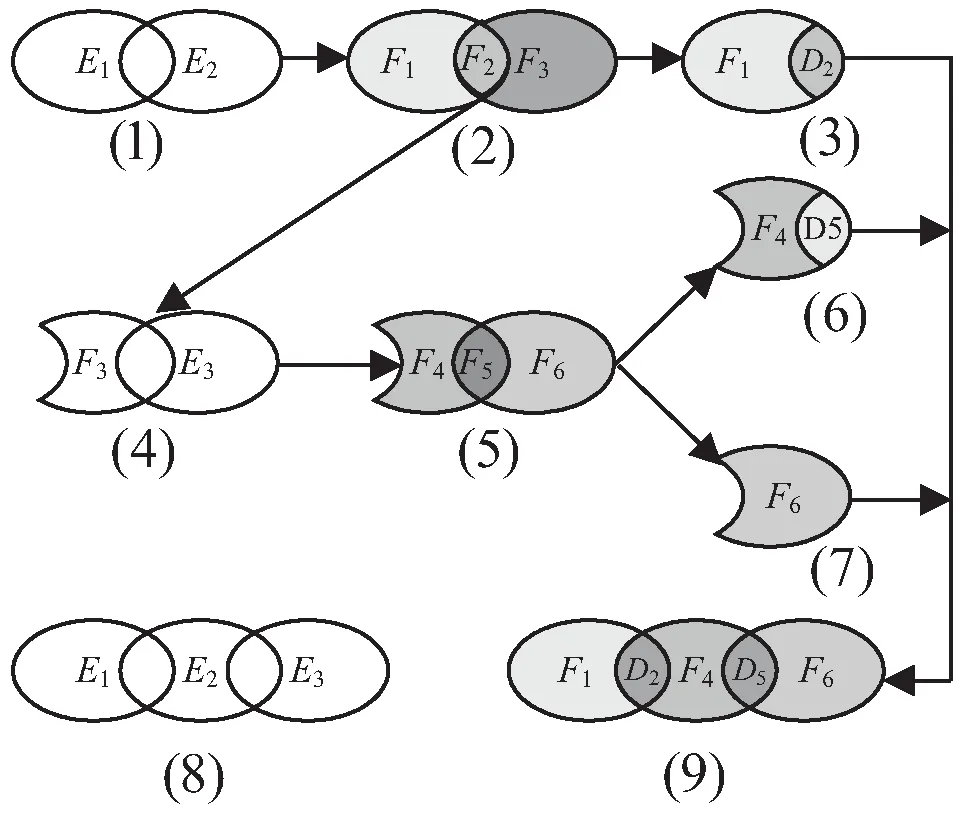
For(j=0;j { (2)Ej=Ej-Fj,j+1;Ej+1=Ej+1-Fj,j+1/*将重叠区域中的点云去掉*/ } 步骤二:D=D∪Ej;/*将最后的点云归到整体点云中*/ 步骤三:用1.2节提出的分组随机精简方法以精简率r对整体D进行精简,使精简率到达要求。 END //算法结束 算法相关说明如下: (1)算法第(2)步:等式Ej=Ej-Fj,j+1,Ej+1=Ej+1-Fj,j+1将重叠区域中的点云去掉,在下一轮中参与操作的Ej+1要将已经精简过的部分排除出去,目的是防止在下一轮精简时不再对已经精简过的部分再次精简,避免过度精简,保持整体点云精简率的一致性。 (3)步骤二中等式D=D∪Ej是将排除了重叠区域点云的最后点云Ej并入整体中。 多视角点云精简算法的计算过程可用图2进行示例说明。图2(9)是待精简的三个有重叠区域的多视角点云。在算法的循环第一轮,首先对E1和E2进行处理;第(1)和(2)步首先将E1和E2点云分割为三个区域:重叠区域点云F2和非重叠区域点云F1、F3,如图2(2)所示。对重叠区域点云F2进行精简得D2,将F1和D2并到整体点云中(图2(3))。在算法的循环第二轮,对F3和E3进行同样处理,得到F4、F5、F6点云(图2(5)),将它们并到整体点云中,形成了精简了重叠区域的整体点云(图2(8))。最后对图2(8)点云再进行一次精简,使精简率达到要求。 图2 算法样例 使用Kinect V2作为深度数据采集的设备,Kinect V2的深度摄像头适用于室内弱光的环境,所以该文选择在白天关闭照明的室内进行深度信息采集。在程序实现时,采用VS2015作为编译环境,并且使用PCL点云库和OpenCV作为第三方编程库。所有程序代码在PCL点云库基础上进行算法改进,采用C++实现,运行于Windows 10 64位系统,Inter(R)Core(TM)i7 - 7700HQ CPU@2.80 GHz处理器、8G内存的笔记本电脑上。图3为Kinect拍摄场景和采集对象水果篮子、打印机。 图3 采集对象和场景 图3中该文使用的圆盒高3厘米、直径10厘米。Kinect V2放置在高6厘米上的矩形石块上,圆盒距离Kinect V2 23厘米。建模物体水果篮子高5厘米、长轴15厘米、短轴11厘米。建模物体打印机长17厘米、宽7厘米、高5厘米。 以水果篮子为例,该文使用Kinect V2对建模物体分别从正面、左侧60°、右侧60°三个视角进行采集,图4中的A、B、C为Kinect V2采集到的原始点云。随后要对原始点云进行预处理,去除离群点。采用PCL点云库中RadiusOutlierRemoval滤波器对点云去除离群点。图4中的D、E、F,在原始点云预处理之后,使用ICP算法[17]把正面、左侧60°、右侧60°的3片点云配准成一个整体后除去下面的圆盒点云。图4中的G、H、I为配准成一个整体点云的正面、左侧、右侧视图。 图4 点云采集和处理 分别使用基于包围盒子的精简算法和该文提出的精简算法对原始点云进行对比实验。共进行三次对比实验。基于包围盒子的精简算法每次只对整体点云精简一次,精简率分别为75%、50%、25%。而文中算法每次实验是以精简率rc对先重叠区域进行精简和再以精简率r对整体点云D进行精简;在实验中,通过调整(r,rc)使三次实验总精简率分别为75%、50%、25%。在本实验中,当(r,rc)的值为(r=80%,rc=93%)、(r=75%,rc=70%)、(r=40%,rc=60%)时,文中算法总的精简率分别达到75%、50%、25%,并且精简效果最好,结果如图5所示。 图5 基于包围盒子点云精简算法和文中算法精简效果对比 (列为精简率(%),行为精简算法和视图分布) 从图5可以看到: (1)在75%精简率下,基于包围盒子的精简算法效果图的正面视图跟文中算法正面视图相比,可以明显看到基于包围盒子的精简算法让原始点云的表面变得平滑,并且达到正面视图25%左右的面积。在相同的位置下原始点云图片可以明显看到纹理细节的起伏,而文中算法相比原始点云,只是点云整体变“薄”了,但纹理起伏还是非常明显的。 (2)在50%精简率下,基于包围盒子的精简算法正面视图将近一半的面积变得平滑,而文中算法还能看到更多的纹理细节,仅比精简率75%的点云厚度更加“薄”一些。在左侧视图中,基于包围盒子的精简算法中,视图中间部分的“空洞”开始被填补上,“空洞”已经变小。而相同的位置,文中算法还能明显看到“空洞”的存在。 (3)在25%的精简率下,基于包围盒子的精简算法中的平滑部分已经扩散到整个点云,从正面视图、右侧视图,左侧视图中已经完全看不到任何纹理细节,并且由于包围盒子设置过大,导致点与点之间的空隙非常大。文中算法由于缺少足够点云的支撑,也开始慢慢出现空洞,但是从正面视图还可以看到纹理细节起伏。 图6是用两种精简算法对打印机点云进行精简的效果图。实验中,参数(r,rc)取值与前面一样。从图6可以看出,基于包围盒子的精简算法和文中精简算法精简的效果差别不大。由于这次实验对象为打印机,由于打印机的纹理呈现规则规律变化并且表面纹理变化不大。相比于图5对水果篮子作为实验对象来说,使用文中精简算法和基于包围盒子的精简算法对打印机在相同精简率情况下精简效果差别不大。 图6 基于包围盒子点云精简算法和文中算法精简效果对比(列为精简率(%),行为精简算法和视图分布) 综上所述,可以看到: (1)基于包围盒子的精简算法对分布不均匀的点云,尤其是由多个多视角点云配准而成的组合点云,无法有效地保持纹理和轮廓等细节,因为该算法在精简过程中不考虑点云的分布情况,而文中算法对这种类型的点云能有效地保持纹理和轮廓等细节,因为该算法通过排序和分组,在一定程度上按点云分布进行精简,点云密集的地方多删一些,分布少的地方少删一些。 (2)从纵向来看,精简率越低,保留下来的点云数量就越少,占用的存储空间也就越少,能节省大量曲面重建的时间和计算资源,但是细节丢失的也多。 (3)从上述两个实验可知,文中算法对于拥有纹理呈现不规则并且变化幅度较大的精简对象,在一定精简率的情况下,能更好地保留精简对象的纹理细节。 该文提出一种面向局部重叠区域的多点云序列的多视角点云精简算法。使用包围盒子提取多点云序列中两个相邻点云的重叠区域内的点云,将它们划分成重叠区域点云和非重叠区域点云;用一个分组随机精简算法对重叠区域内的点云进行精简。对所有的重叠区域点云精简之后,与非重叠区域点云再合并成一个整体点云,根据精简率的要求再对整体点云进行一次精简。对文中精简算法和基于包围盒子的精简算法进行实验对比。实验结果表明,在相同的精简率下,文中精简算法比基于包围盒子的精简算法更能减少对目标物体点云的细节破坏,最大程度上保留目标物体的点云细节和特征。下一步,将工作重点放在点云精简过后的曲面重建问题上,并开发一个包含点云采集、点云预处理、点云配准、点云精简、曲面重建等功能的实时快速三维重建系统。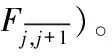
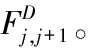
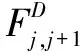
2 实验结果与分析
2.1 数据采集与预处理


2.2 实验结果分析


3 结束语

