基于CRNN的CSI动作识别

丁文超，张俊宝，阴庚雷

(中原工学院 计算机学院，河南 郑州 450007)

0 引 言

随着Wi-Fi技术的发展以及相关硬件价格的下降，生活中各种场所几乎均有Wi-Fi信号的存在。Wi-Fi信号不仅能传输数据，利用其信道状态信息还能进行人体动作识别[1]。

传统的动作识别需要借助如加速度计、陀螺仪等接触式传感设备[2]对用户进行监测来识别用户的动作，又或者是借助摄像头等非接触设备的基于视觉[3]的动作识别。相较于传统的识别方式，基于CSI的动作识别利用的是环境中广泛存在的Wi-Fi信号，具有不依赖特殊传感器、成本低、易扩展、不存在隐私泄露等优点。

但是当前应用大部分都依赖于手工选择子载波，构建分类特征。因此，该文提出一种基于学习的识别方法，无需专业知识构建Wi-Fi传播模型，即可进行训练识别。

1 相关工作

由于采集数据时网卡报告了多组子载波的CSI，且不同的子载波对于环境变化的敏感度不同，所以要选取合适的子载波来提取CSI数据。WiFall[4]将30组子载波上的CSI取平均值作为训练数据来检测摔倒动作的发生。LBR[5]选取CSI方差第二大的子载波作为有效子载波来提取CSI。上述方法均根据某个统计值来选择子载波，需要大量的时间研究数据从而选择合适的统计特征。该文提出一种基于SOM[6]聚类的子载波选择方法。相同的动作，某个子载波上的CSI数据聚类生成多个簇，则说明CSI存在多种变化模式数据间差异较大，数据采集过程中该子载波易受环境干扰。因此对于每个动作，该文选取所有子载波聚类后生成簇较少的子载波作为有效子载波。

在训练特征的选择上，CARM[7]使用离散小波变换从不同时间尺度的不同活动中提取频率分量作为特征。WiSee[8]从手势动作中提取对应的多普勒频移特征来识别手势。两种方法均需手动设计特征。该文提出使用GASF[9]方法将CSI转换成图像从而利用CNN强大的特征提取能力自动提取特征。

由于实验对象的运动速度以及采样频率的差异，相同动作所收集到的CSI数据长度可能不同，但神经网络输入数据的长度需要保持一致。所以要对收集到的CSI数据进行截取，以保证数据长度相同，并且截取到的部分需要包含动作发生的整个过程。WiFinger[10]根据统计特征来检测手势动作的起始点和结束点。文献[11]直接采用了人工截取的方式。上述方法需要大量的人力与计算资源来截取数据。文中的CRNN网络使用CTC[12]作为损失函数，能够使网络自动对齐输入数据中发生动作的部分，无需对数据进行截取。

深度学习网络需要大量的数据来进行训练从而防止模型过拟合，但是人工采集大量的数据往往是不容易的。因此，该文通过添加噪音、缩放、滑动平均等方法增加数据量，从而提高模型的鲁棒性。

2 信道状态信息

CSI代表了信号在传输过程中所产生的时延、幅度衰减以及相位偏移等变化。换句话说，CSI表征了附近环境的无线特性。假设发送端信号为X(f,t)，接收端信号为Y(f,t)，那么有[1]：

Y(f,t)=H(f,t)·X(f,t)+n

(1)

其中，H(f,t)为信道频率响应矩阵，CSI就是对H(f,t)的估计。n为高斯白噪声。对于单个子载波，CSI的形式如下：

Hi=|Hi|ej·sinθ

(2)

其中，|Hi|和θ分别表示CSI的幅度和相位。由于商用网卡接收到的两个连续的CSI间相位差可能很大，因此该文只使用CSI的振幅进行动作识别。

3 方法设计

图1所示为方法流程，由信号采集、数据处理、训练预测三个阶段组成。其中信号采集阶段将在第3章详细阐述。

图1 方法流程

3.1 数据预处理

3.1.1 滤波去噪

由于人体动作的频率较低以及环境中高频噪音存在，所以原始CSI需要滤除高频分量，这里使用常用的巴特沃斯低通滤波器进行滤波[1]。巴特沃斯低通滤波器的增益G2(ω)为：

(3)

其中,n表示滤波器的阶数，ωc表示截止频率即功率下降为-3分贝时的频率，G0是直流增益。频率低于ωc的部分会以G0的增益通过，而频率高于ωc的就会被抑制。由于手部动作频率范围在0.3 Hz到4.5 Hz之间[13]，因此设置截止频率为5 Hz，考虑到滤波效果与计算成本滤波器阶数设置为5。图2所示为滤波前后对比，可以看出滤波后曲线变得平滑高频噪声被抑制。

图2 低通滤波前后CSI幅值对比

3.1.2 子载波选择

SOM[6]是一种无监督聚类的神经网络，通过学习自动对输入进行聚类，且能保持数据的拓扑结构不变。SOM由输入和输出(竞争两层)构成，采用竞争学习的方式进行训练。首先将网络权重初始化，接着每个输入的样本遍历竞争层中的每个节点，计算两者之间的距离(通常为欧式距离)，选取距离最小的节点作为获胜节点。

接着用随机梯度下降法更新获胜节点及其邻近节点的权重向量使它们向输入向量移动。输出节点v的权值更新公式为：

Wv(s+1)=Wv(s)+θ(u,v,s)·α(s)·(D(t)-Wv(s))

(4)

其中，Wv为权重向量，s为迭代次数，D(t)为当前输入向量，u为获胜节点，θ(u，v，s)为s下给出u和v之间距离的邻近函数，用来确定获胜节点对其近邻节点的影响强弱。α(s)是一个单调递减的学习率。对每个输入向量这个过程会重复进行直到达到提前设置的循环次数λ。

该文设置输出层SOM神经元的数量为3进行聚类，图3所示为上下挥手时不同的四个子载波上的CSI聚类后的结果。样本数量为50，可以看到子载波3聚类后只有一个簇，说明数据内在的分布较一致，受环境干扰较小。子载波1、2、4聚类后均生成多个簇，说明同一个子载波上的CSI间差异较大。因此对于上下挥手动作，选择提取子载波3上的CSI作为训练数据。

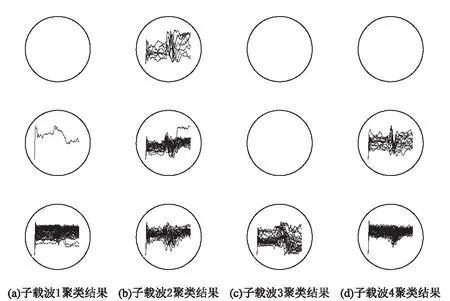
图3 上下挥手的四个子载波聚类结果

3.1.3 数据扩增

相较传统模型，深度学习的参数非常多，故有很强的拟合能力，从而也就需要更多的数据来避免过拟合的发生。但收集和标记大量的数据是耗时耗力的。通过现有的样本进行数据扩增创建新的样本，能够利用有限的数据有效地提高分类性能[14]。该文采取了多种数据扩增方法包括：

(a)添加噪声，CSI序列加上高斯随机噪声序列n。

(b)缩放，CSI序列乘以缩放系数s。

(c)降采样，设置降采样因子m，保留CSI序列中间隔为m的采样点，其余采样点舍弃。

(d)滑动平均，采样点i的值由滑动窗口w内CSI数据的平均值代替。

(e)截取，使用长度为l的窗口在CSI序列上截取数据。

图4所示为使用不同方法所产生的新样本。可以看到一个样本能生成多个虚拟样本。且所生成的样本保留了CSI的变化模式。

图4 应用不同数据扩增方法得到的新样本

3.1.4 CSI转换为图像

CNN能够自动高效地从图像中提取特征。因此该文没有手工设计特征，而是使用GASF[9]方法将接收到的CSI编码为图像，使用CNN提取特征。设X={x1,x2,…,xn}为滤波后的CSI序列，先通过

(5)

GASF=[cos(φi+φj)]1≤i,j≤n

(6)

于是有：

GASF= [cos(φi)·cos(φj)-sin(φi)·

sin(φj)]n×n

(7)

(8)

图5所示为6种手势动作的CSI，通过转换得到的GASF图像，可以看到不同的动作生成的图像有不同的纹理特征。

图5 不同手势的CSI转化得到的图像

3.2 训 练

文中的CRNN由CNN、RNN构成，训练时使用CTC作为损失函数。网络结构如图6所示。

图6 网络结构

3.2.1 卷积神经网络

首先使用卷积神经网络[15]来对图像提取特征，卷积网络部分由四个卷积模块组成，每个卷积模块由两个二维卷积层加上一个池化层构成。卷积层l的卷积计算公式为：

(9)

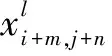
池卷积层的池化操作能够减少模型的计算量和参数个数，防止过拟合。该文使用了最大池化，其公式为：

fpool=Max(si,j,si+l,j,si,j+1,si+l,j+1)

(10)

其中，fpool是池化后的结果。si,j是特征图张量上位置(i,j)上的元素。该文使用的池化核大小为2×2。

3.2.2 长短期记忆网络

由于CSI是时间序列数据，所以接下来使用两个长短期记忆(long short-term memory，LSTM)层对CSI序列时间上的变化进行建模。LSTM[16]是一种拥有三个“门”的特殊网络结构，包括遗忘门、输入门、输出门。输入门选择保留的信息，遗忘门选择被遗忘的信息，输出门决定哪些状态信息需要输出，如公式(11)所示。

(11)

其中，i，f，o，g分别表示输入门、遗忘门、输出门的输出以及输入的单元状态。σ，φ分别为sigmoid、tanh激活函数，ht-1，xt分别为上一时刻的输出和当前时刻的输入。当前时刻的单元状态ct为：

ct=f⊙ct-1+i⊙g

(12)

其中，ct-1为上一时刻的单元状态，⊙表示元素乘。由当前时刻的输出门输出ot和单元状态可得当前时刻的输出ht为：

ht=ot⊙tanh(ct)

(13)

3.2.3 CTC损失函数

由于CSI序列长度不一致，那么训练前每个样本都需要标记出发生动作的片段在整个CSI序列中的位置，从而截取得到长度一致的输入数据，该文使用CTC[12]损失函数不需要对数据进行截取。LSTM提取完特征后由两个全连接层和Softmax层进行分类，分类结果作为CTC损失函数的输入，此外还需要提供输入长度、标签、标签长度。

(14)

用B表示映射函数，消除重复的标签和空白标签，例如：

B(_,a,a,b,b,c,c,_)=(a,b,c)

(15)

因此输出序列路径为μ的概率可以表示为经过映射后为μ的所有π的概率之和，即：

(16)

CTC损失函数定义如下：

CTC(X)=-logP(μ|X)

(17)

CTC算法通过最大路径解码所解得的概率最大的输出序列路径为：

(18)

其中，π*为T帧输入序列的后验概率最大的CTC输出序列路径。

4 实验设计

4.1 数据采集

将一台装有英特尔5300网卡，系统内核版本为4.1.10的HP Pavilion15笔记本电脑作为接收端接收信号。一个支持802.11n 协议的MERCURY MW305R路由器为发射端发送信号。使用Halperin[17]发布的CSI工具包来修改网卡驱动。设置路由器的工作频率为2.4 G，发包频率为20 Hz。由于发射端有两根天线，接收端有三根天线，每个天线对上有30个子载波。因此接收到的CSI数据为2*3*30的复数矩阵。

图7(a)所示为实验环境。实验对象站在笔记本和路由器之间的桌子前做如图7(b)所示的6种手势动作，每个手势采集50组数据，共计300组数据。使用240组数据训练模型，剩余60组数据对训练好的模型进行测试。

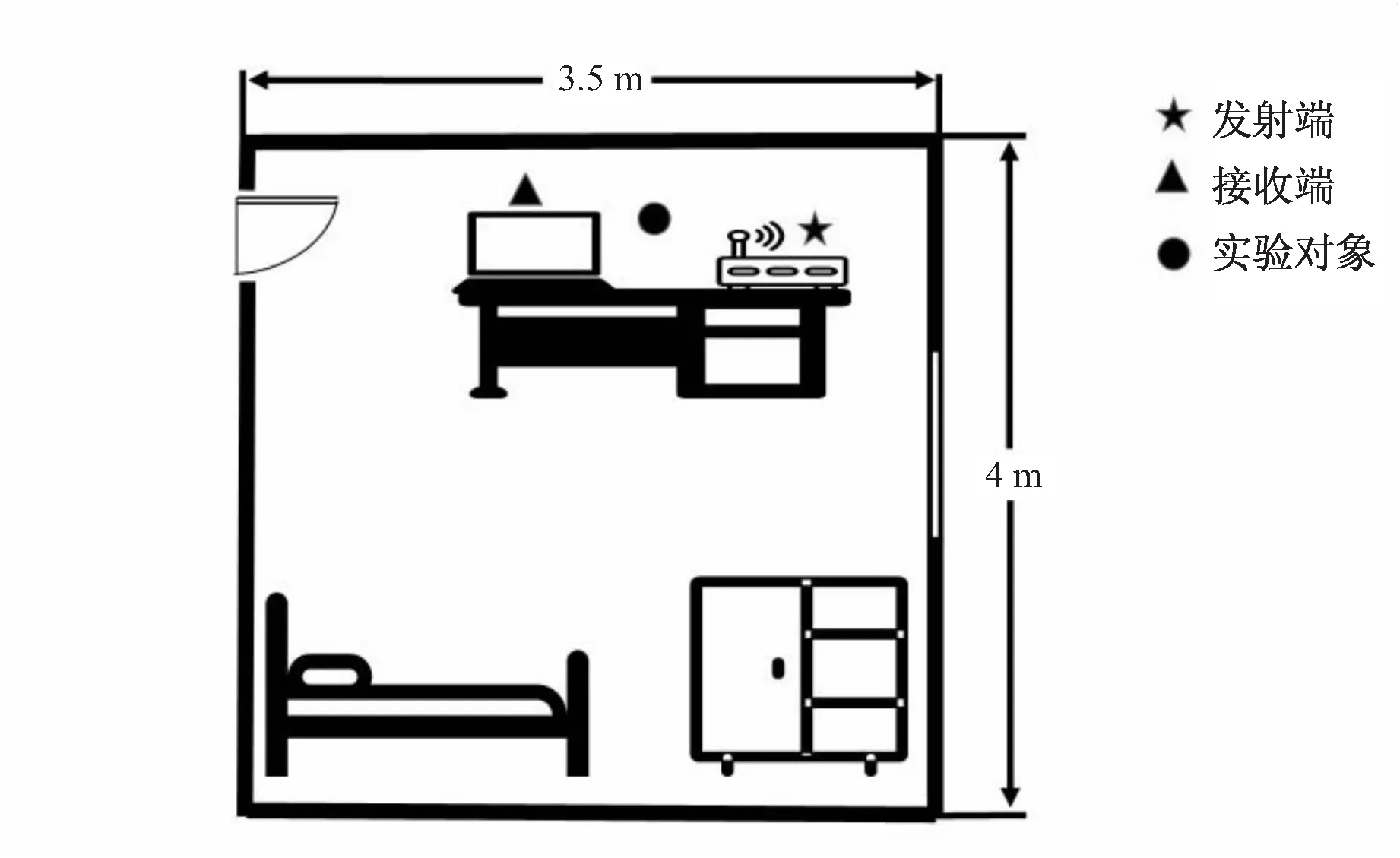
(a)实验环境平面图

(b)6种手势

4.2 对比分析

该文做了一系列对照实验来对比分析提出的方法的有效性。

4.2.1 不同的子载波选择方法

为了验证提出的基于SOM聚类的子载波选择方法的有效性，对照实验使用了WiFall[4]的所有子载波求平均、LBR[5]的选择CSI方差第二大的子载波进行对比。仅改变子载波选择方法，其他步骤相同，实验结果如表1所示。

表1 不同的子载波选择方法结果对比

结果表明直接对所有子载波上的CSI求平均，结果准确率较低，原因可能是不同的子载波对动作和环境的敏感度不同，直接求平均值将各种环境因素的影响叠加到一起，使得CSI中的有效信息被掩盖。选取方差第二大的子载波，准确率虽然有所提高，但是由于CSI易受环境噪音影响，较大的方差可能是由于环境噪音变化引起的，而且不能保证相同动作的CSI变化模式的一致性。通过聚类选择子载波能够保证相同动作的CSI数据内部的一致性，不会出现异常数据，准确率较高。

4.2.2 不同的网络结构

将SignFi[18]使用的CNN及文献[19]所使用的LSTM作为对照，并把使用交叉熵损失函数的CRNN也作为一种不同的网络进行对比，结果如表2所示。

表2 不同的网络结构结果对比

可以看到仅使用LSTM由于模型参数数量较少因此拟合能力较弱。使用CNN能够达到相对较高的准确率。相较于仅使用CNN或LSTM，同时使用CNN、LSTM能综合利用两种网络结构的优势，准确率较高。使用CTC损失函数不仅不需要对CSI进行截取，而且能够有效地识别发生动作的CSI序列片段，从而提高模型的分类准确率。

4.2.3 不同数量的训练数据

基于学习的识别方法要求有大量的数据训练模型，本小节通过对比实验探究不同数量的训练数据对于识别准确率的影响。分别使用120组数据，240组数据，与文中使用的240组数据并对数据扩增的方法作对比，结果如表3所示。

表3 不同数量的训练数据结果对比

可以看到随着训练数据的增加模型的分类准确率也随之增加，模型对训练数据的数量有较高的要求。虽然大规模采集数据是不容易的，但是通过数据扩增的方法，能够在原有数据的基础上增加数据的多样性，有效提升模型的准确率。使得基于学习的方法也能够以较低的数据成本达到较高的识别效果。

5 结束语

提出了一种基于SOM聚类的子载波选择方法，并将CSI数据序列转换为图像，通过CNN、LSTM构成的网络使用CTC损失函数进行训练分类。在数据预处理和模型训练中，采用聚类和深度学习的方法代替传统的基于手工设计特征的方法，并利用现有样本进行了数据扩增。实验结果表明，该方法能够在数据量较小的情况下达到较高的识别准确率，且无需手工设计特征。下一步将会致力于研究提高模型的泛化能力。