基于Kriging模型和粒子群算法的不等厚永磁电机优化设计

黄 锐，郑 东

(西南交通大学 机械工程学院，成都 610031)

0 引 言

经国内外学者研究发现，对永磁体磁极进行优化，采用不等厚永磁体结构，不仅可以节省永磁体材料、简化磁极加工，而且可以有效降低电机齿槽转矩，但同时也会导致电磁转矩性能下降。文献[1]采用磁极分段的方法，将Bread-Loaf型磁钢等效成一系列同圆心角磁极结构的组合，并利用该模型分析了偏心距与极弧系数对电机气隙磁场的影响。文献[2]分析了偏心磁极结构对磁场分布的影响，利用等效槽表面虚拟电流的方法，进一步考虑了开槽的影响，结果表明，采用偏心磁极结构能够降低齿槽转矩。文献[3]针对含偏心磁极的永磁同步电机，采用离散思想和磁场叠加原理，建立了气隙磁场、齿槽转矩、反电动势以及电磁转矩解析模型，并进一步分析了不等厚磁极参数对电磁性能的影响。

电机性能优化目前国内研究比较多，大多都是以电机性能为优化目标，以电机结构参数为自变量，通过优化算法来找到最优的参数组合。文献[4]以异步起动永磁电机为研究对象，利用响应面法，建立了转子尺寸与效率和起动转矩之间的响应模型，利用布谷鸟算法得到了最优结果。文献[5]分析了电机各项参数对电机性能的影响，以此构建了多目标优化函数，得到了多目标优化下最优控制参数组合。文献[6]将Kriging代理模型应用于直线感应电机的性能优化，减少了仿真时间。

虽然目前很多研究认为不等厚永磁体可以降低齿槽转矩，但其忽略了不等厚永磁体也会导致平均电磁转矩降低。本文将通过建立Kriging代理模型、结合多目标粒子群算法，找到最优的参数组合，不仅可以有效降低齿槽转矩，也能使电机有较高的平均电磁转矩，而且还能节省永磁体材料。

1 磁极参数对电机性能的影响

等厚磁极模型如图1(a)所示，从图1(a)中可以看出,等厚磁极模型的内弧圆圆心和外弧圆圆心位于同一点O，永磁体厚度hm的值也保持不变。Rm为内弧圆半径，Rr为外弧圆半径，O为圆心。

不等厚磁极模型如图1(b)所示，相比于传统的等厚磁极结构，内弧圆圆心和外弧圆圆心不在同一个点上，永磁体内圆弧中心O′偏离圆心O距离为d，半径为Ri，hm为永磁体中心处厚度。

如图1(b)所示，根据三角函数推导圆心O到内弧圆距离Rrj:

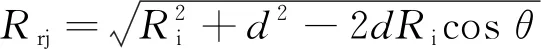
(1)

由式(1)可以看出,Rrj是关于Ri、d、θ的一个函数。其中磁极内弧圆是以O′为圆心，半径为Ri的圆，磁极外弧圆是以O为圆心，半径为Rr的圆，因此Ri又可表示：

Ri=Rr+d-hm

(2)

将式(2)代入式(1)，可得：

(3)

由于本文是内弧偏心的电机结构，因此Rr是一个定值，从上式可以看出,Rrj其实是一个关于hm、d、θ的一个函数，随着角度θ的不同，内弧圆半径Rrj的大小也不同，因此形成了不等厚磁极结构。因此,接下来研究不同的永磁体中心厚度hm和磁极偏心距离d对电机性能的影响。

图2为磁极参数对齿槽转矩的影响。从图2中可以看出，磁极偏心距离d对齿槽转矩的影响较大，永磁体中心厚度对齿槽转矩影响较小。图3为磁极参数对电磁转矩的影响。磁极偏心距离d越小，永磁体中心厚度hm越小，相应的电磁转矩就越小；同时磁极参数的改变也会导致永磁体体积的改变。图4为磁极参数对永磁体体积的影响。从图4中可以看出，磁极偏心距离d越小，永磁体中心厚度hm越大，相应的永磁体体积就越大。因此，需要通过优化算法来求得小齿槽转矩，大电磁转矩，小永磁体体积的最优磁极参数组合。

图4 磁极参数对永磁体体积的影响

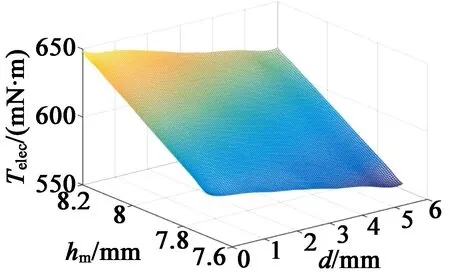
图3 磁极参数对电磁转矩的影响

图2 磁极参数对齿槽转矩的影响

2 Kriging代理模型的建立

不等厚磁极参数对电机的齿槽转矩、电磁转矩、永磁体体积都有很大的影响。但是不同的hm和d有非常多的组合，每一个hm和d的组合都需要对电机模型进行修改，再重新仿真，这样的过程需要花费大量的时间。因此，本文将利用有限的样本数据，通过建立Kriging代理模型，来预测不同的hm和d的组合对电机性能的影响。

代理模型可以利用有限点的响应来构造近似的函数表达式，以此对未知区域的响应进行预测[7]，Kriging代理模型和神经网络、响应面模型相比，具有明确的数学表达式，不受随机误差的影响，构建模型需要很少的样本点，而且具有较高的精度，是一种对空间分布的数据求线性最优、无偏内插估计的插值方法[8]。

将磁极参数hm和d用矩阵x表示，电磁转矩、齿槽转矩、永磁体体积用矩阵y表示。

(4)

式中：n为样本数；xi为第i个样本点的磁极偏心距离d，永磁体厚度hm；yi为当永磁体不等厚参数为xi时的电机性能；Tcogi,Teleci,Vi分别为第i个样本点的电磁转矩、齿槽转矩和永磁体体积。

xi和yi之间的关系可以写成多项式回归模型F(β,x)与零均值正态分布随机过程ε(xi)的叠加：

yi(xi)=F(β,x)+ε(xi)

(5)

ε(xi)的协方差矩阵：

cov[ε(xi),ε(xj)]=σ2R[ε(xi),ε(xj)]

(6)

式中：σ2为随机过程的方差；R[ε(xi),ε(xj)]为样本i,j之间的相关函数；i,j=1,2,3，…,n。对于一个K维变量空间，Kriging函数表示：

(7)

式中：θh表示第h个变量对目标的贡献度；Ph为表征函数平滑性的参数。消除建模误差的可能性的概率密度函数：

I为n×1阶单位矩阵，等式两边去自然对数有：

R为所有正交采集样本的相关矩阵：

(10)

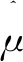
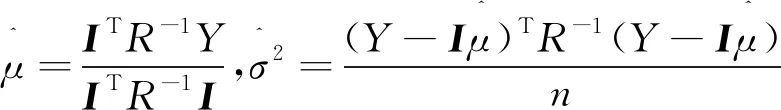
(11)

将式(11)代入式(9)，忽略常数项可得：

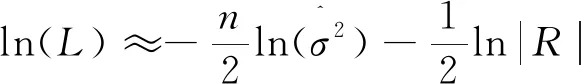
(12)

式(12)的取值仅和θh和Ph相关，因此建立代理模型的问题转化为寻最优的θh和Ph使式(12)取得最大值。

当获得最优的θh和Ph后，对于不同的hm和d的组合可通过式(13)预测相应的电机性能，包括永磁体体积。

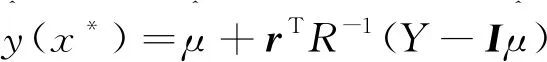
(13)

式中，r为待测未知hm和d的组合x*与初始采集样本的相关向量：

(14)

至此，不等厚永磁直流电机参数对电机性能影响的代理模型建立完毕，将表1中的数据代入模型中，便可得到任意hm和d组合下的电机电磁转矩、齿槽转矩和永磁体体积，节省了大量的仿真计算时间。

表1 样本数据

3 多目标优化函数的构建

多目标优化问题包含m个目标函数，K个决策变量和n个约束条件，由于目标函数间的矛盾性，使每个目标函数同时达到最优值的解是不存在的[9]。因此得到的解并不是所有子目标的最优解。本文中将齿槽转矩、电磁转矩、永磁体体积作为三个目标函数，采用权重法将多目标优化问题转化为单目标问题，即:

式中：f为适应度值，其大小介于0～1；λ1，λ2，λ3为对应目标的权重系数，λ1+λ2+λ3=1；Tcog，Telec，V是随机磁极厚度hm和偏心距离d组合下的齿槽转矩、电磁转矩、永磁体体积；Tcog_max，Telec_max，Vmax，Tcog_min，Telec_min，Vmin是满足约束条件下的齿槽转矩、电磁转矩、永磁体体积的最大值和最小值。

由于本文研究的是小型电机，通过查阅文献，气隙长度需要在0.3～0.8 mm之间，同时当磁极偏心距离d大于6 mm以后会导致电磁转矩急剧下降，因此设置磁极参数约束条件：

(16)

电机最终的优化目的为较小的齿槽转矩、较高的电磁转矩和较小的永磁体体积。通过观察式(15)，需要目标函数的第一项和第三项越小越好，而第二项越大越好，因此，我们将式(15)改变一下形式，将第二项的分子和分母交换一下：

通过以上分析可知，f的值越小，说明电机性能越好，因此最终将电机的优化问题转变为了求目标函数的最小值问题：

F(x)=minf(hm,d)

(18)

至此，电机的目标函数构建完成。上述目标函数不仅巧妙地将电机的优化问题转变为了求目标函数的最小值问题，而且还可以根据实际工程的不同需要，修改λ1、λ2、λ3的值。比如企业需要更多地考虑齿槽转矩，那么可以将λ1的值设置得更大；如果要更多地考虑电磁转矩，那么可以将λ2的值设置得更大。提高了该优化函数在实际工程问题的实用性。

4 粒子群算法优化模型

粒子群算法是美国学者Kennedy和Eberhart在受到鸟类觅食活动的启发后而提出的一种群体智能算法[10]。粒子群算法与遗传算法较类似，但区别在于，粒子群算法较为简单，没有遗传算法的交叉和变异，通过追随当前搜索到的最优值来向全局最优解逼近。粒子群算法收敛速度快，其模型也更为简单，易于实现，擅长处理多极值函数全局优化问题。基于上述优点，粒子群算法非常适合解决电机优化这一类问题。

粒子群优化算法是根据个体的适应度值(即目标函数的值)，使种群一步一步朝着更好的区域移动[11]。在算法的整个迭代过程中，粒子每更新一次位置，就计算一次适应度值，通过比较新粒子的适应度值、个体最优适应度值、群体最优适应度值来更新个体最优极值和群体最优极值，如图5所示。

图5 优化流程图

每次迭代过程中，粒子通过个体极值和群体极值来更新自身速度和位置，更新公式如下：

(19)

(20)

粒子群算法参数设定完成以后，便可将目标函数和粒子群算法结合起来，粒子群算法产生随机初始粒子，然后通过Kriging代理模型预测相应的电机性能参数，再将电机的各项性能参数代入目标函数，如此循环下去，直到满足迭代次数要求，并输出目标函数的最小值以及相应的磁极厚度hm和磁极偏心距离d。

前文已经提到过权重因子λ的大小反映了对某个目标优化的重视程度，λ的取值不同，最后优化的结果也不同，因此本文根据λ的不同取值,设计两个结构优化方案。方案一：目标权重因子λ1=0.6,λ2=0.2,λ3=0.2;方案二：目标权重因子λ1=0.2，λ2=0.6,λ3=0.2，粒子种群规模设置为20，最大迭代次数设置为200,ω=1,c1=c2=1.5。算法的收敛曲线如图6所示。

(a) 方案一

在方案一的目标函数下，算法得到的最优组合为hm=8.2mm，d=5.5mm，目标函数的最小值fmin=0.337；在方案二的目标函数下，算法得到的最优组合为hm=8.2 mm，d=3.5 mm，目标函数的最小值fmin=0.875。根据优化结果对有限元模型进行修改，并在Maxwell进行仿真，将两种优化方案和原始结构(hm=8 mm，d=0)的电磁转矩和齿槽转矩进行对比，电磁转矩和齿槽转矩曲线如图7和图8所示，永磁体体积对比如表2所示。

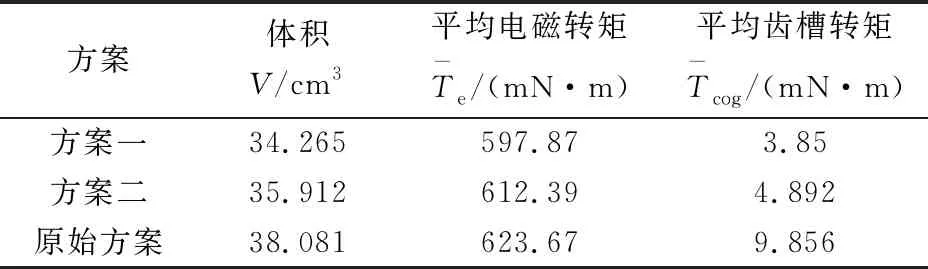
表2 三种方案性能对比

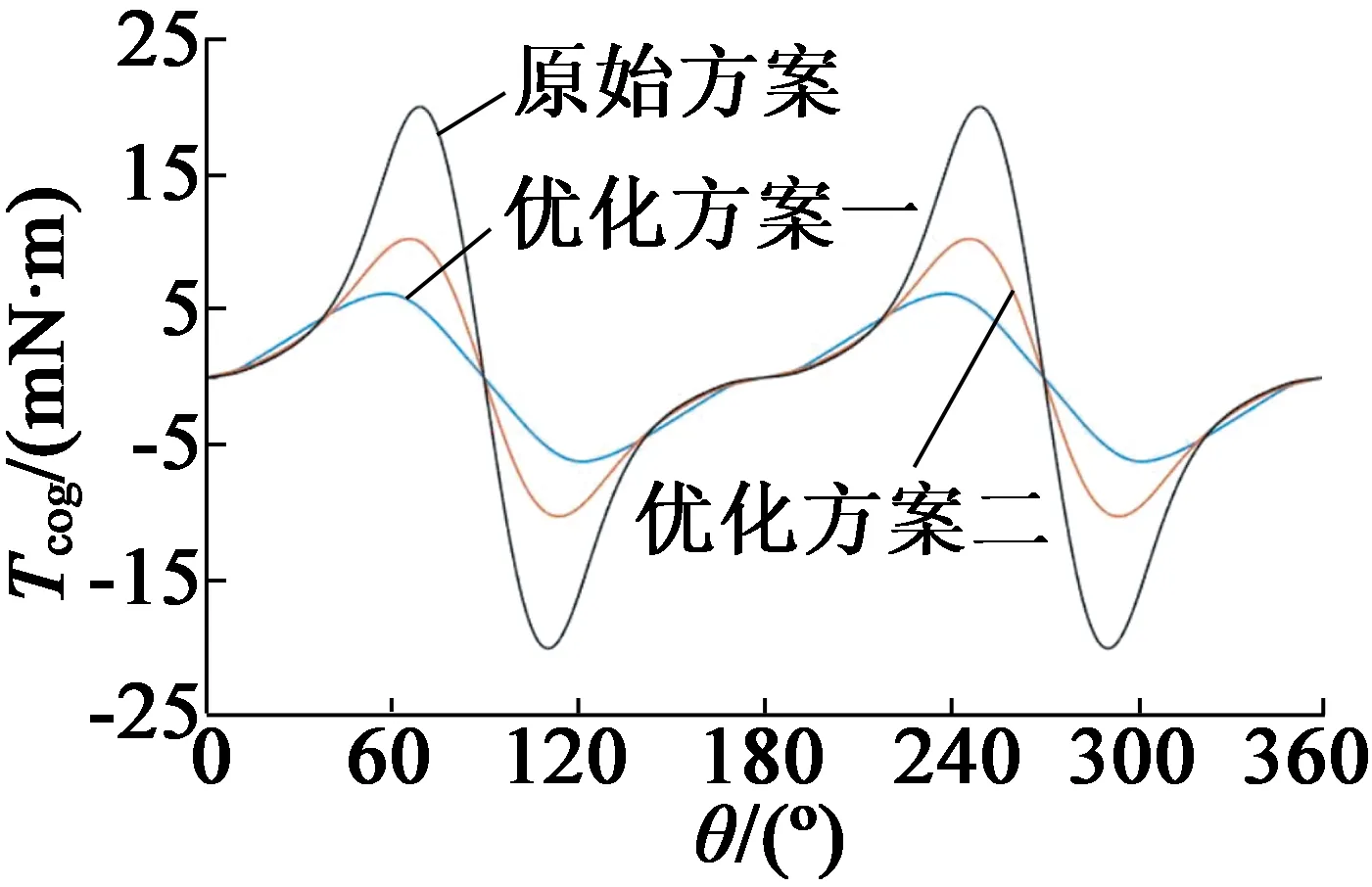
图8 齿槽转矩对比曲线

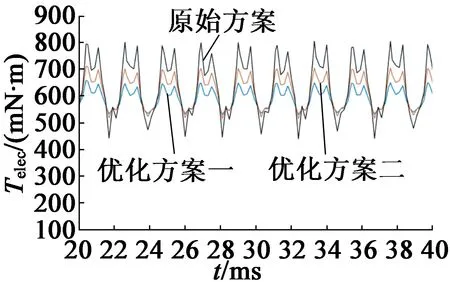
图7 电磁转矩对比曲线

从图7、图8、表2中可以看出,优化方案一和优化方案二相比，方案一齿槽转矩相比于原始方案下降了61%，方案二齿槽转矩相比于原始方案下降了50%，方案一的平均电磁电磁转矩相比于原始方案下降了4.1%，方案二的平均电磁电磁转矩相比于原始方案下降了1.8%。虽然都是采取了不等厚永磁体结构，但是因为权重系数的不同，方案一更希望齿槽转矩越小越好，而方案二更希望电磁转矩越大越好，因此，方案一的齿槽转矩要更小一些，方案二的电磁转矩要更大一些。同时，无论是方案一，还是方案二，永磁体体积都小于原始方案，实现了本文的优化目的，说明了优化算法的有效性。

5 结 语

本文首先研究了不等厚永磁体磁极参数对电机性能的影响，然后将Kriging代理模型和多目标粒子群算法相结合来实现对电机的优化，结果表明，本文的优化算法不仅能够有效削弱齿槽转矩、降低转矩脉动，也能保证较高的电磁转矩，同时还能节约永磁体材料。进一步分析可知，增大磁极偏心距离d，会导致齿槽转矩减小，电磁转矩减小，但同时增大永磁体中心厚度hm，可以弥补磁极偏心引起的电磁转矩减小的问题。同时本文的算法还可以根据不同的需要来改变优化目标的权重系数，实现对电机性能的灵活优化，节约大量的仿真时间，为实际的工程应用提供参考依据。