一种微型压电振动能量发电装置的设计与分析

赵 伟，张健滔, 贺 明

(上海大学 机电工程与自动化学院， 上海 200072)

0 引 言

随着微电子技术、无线电技术的飞速发展，具有计算能力、感知能力和通信能力的无线传感器网络也逐渐大量地应用到生产、生活中[1]。微电子器件和无线传感网络主要依靠传统的化学电池为其供能，但化学电池却存在体积大、更换不方便、成本高等缺点，制约了微电子设备和无线传感网络的发展。为解决微电子器件的供能问题，研究者尝试从周围环境获取能量来为其供电，这样可以减小对化学电池的依赖并且提高供电系统的生命周期[2-5]。目前，环境中存在的能量包括：风能、太阳能、振动能、水能、地热能等。其中，振动能是一种分布广泛、清洁无污染、可再生的能源，如何收集振动能成为了研究的热点。将振动能转化为电能的方式有电磁、静电和压电等方式。

本文设计的振动能量收集器利用压电陶瓷的正压电效应将振动能转化成电能。该能量收集器具有可以持续为外界供电，体积小、易于制作、生命周期长、能量转化的效率高等优点[6-7]，正受到越来越多的关注。研究者已对压电振动能量的采集机理进行了深入研究，开发出了各种微型的压电振动发电装置。Zhao X Q等人设计了一种等尺寸阵列AIN压电阵列采集器，该采集器属于多悬臂梁结构且具有相同的共振频率，一般通过串联或者并联的方式来提高采集器的整体输出性能[8]。Hamid等人设计了一款压电和电磁混合的能量收集装置，可以从人体运动等低频振动中获取能量，从而为可穿戴设备提供电能[9]。Wang Xiang等人设计了一种紧凑型压电振动能量收集器，其采用了多种非线性技术来调节谐振频率并扩宽了收集器的工作频带，从而可以更高效地收集环境中的振动能[10]。Ansari M H等人设计了一种具有两种工作模式的压电振动能量收集器，人或车辆经过时产生的振动会在结构的作用下放大，从而收集器可以产生更多的电能[11]。Zhu Yang等人设计了一种中部放置一块磁铁的振动能量收集器，研究显示，该振动能量收集器不仅有效提高了低频振动下的输出电压，而且还拓宽了工作频带[12]。

本文基于压电效应设计了一款压电振动能量发电装置，为了提高该悬臂梁式发电装置的输出特性，在弹性基板上开了大小一致的矩形槽，以此提高压电陶瓷片所受的应力大小。分析了发电装置的换能原理并且建立了有限元模型，对不同尺寸的模型进行了静力学分析和模态分析，根据仿真结果对压电振动能量发电装置进行尺寸上的优化设计，最终得到了使压电陶瓷产生最大应力和应变的发电装置的尺寸。

1 微型压电振动能量发电装置结构设计

当压电振动能量收集器振动时，压电陶瓷会由于正压电效应而产生电荷，从而可以为微电子设备提供能量[13]。传统的悬臂式振动能量发电装置的结构如图1所示，其结构简单。为了提高传统发电装置的发电能力，本文对其结构进行了改进。

图1 悬臂梁式压电振动能量发电装置结构示意图

考虑在悬臂梁上进行裁剪开槽，这样悬臂梁变形时，可增加压电元件的应力和应变，进而增强其发电能力。初步设定弹性基板的尺寸为50mm×16 mm×0.1 mm，单片压电陶瓷片的尺寸为12 mm×4 mm×0.25 mm，每个凹槽的尺寸为9 mm×1 mm，压电陶瓷与裁剪凹槽的距离是2 mm，压电陶瓷和凹槽均匀地分布在弹性基板上，改进后的悬臂梁式多槽型压电振动能量发电装置如图2所示。

图2 悬臂梁式多槽型压电振动能量发电装置

2 微型压电振动能量发电装置换能原理

悬臂梁及其上面粘贴的压电陶瓷片在外界振动的作用下会产生应变与应力，压电陶瓷片的压电效应使得其内部电荷发生相对移动，压电陶瓷片上、下表面产生符号相反的电荷，且所产生的总电荷量与压电陶瓷受到的外载荷成正比关系。由于压电陶瓷沿厚度方向极化，其振动的主要方向也是沿厚度方向， 因此其压电本构方程[14]：

σp=Ep(εp-d31E3)

(1)

(2)

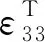
当受到外界振动激励作用时，微型压电振动能量发电装置主要产生一阶弯曲振动，其振动微分方程[15]：

(3)

式中：Me是等效质量；Ce是等效阻尼；Ke是等效刚度；z是等效质量的绝对位移；U是输出电压；αe是机电耦合系数；y是等效质量相对于基座的位移。

根据基尔霍夫电流定律，该微型压电振动能量发电装置所产生的电流：

(4)

式中：RL是负载电阻;Cp是压电陶瓷的等效电容。

所设计的微型压电振动能量发电装置使用了5片压电陶瓷片，其可以采用串联方式或者并联方式连接。当采用并联方式连接时，其输出电流是串联方式连接时输出电流的若干倍，因此压电片并联可以有效提高输出电流[16]。电流较大有利于给电池充电，因此，本文采用了并联方式连接。压电陶瓷的等效电容可以看作5片压电片静态电容的叠加，可以写成[17]：

(5)

式中：bi，Li，hi分别为第i片压电陶瓷的宽度、长度及厚度。

3 微型压电振动能量发电装置有限元分析

3.1 微型压电振动能量发电装置有限元模型

微型压电振动能量发电装置结构主要由弹性层与压电层构成。压电层的压电材料是实现机电耦合的核心材料，对能量转换起决定性作用。压电材料PZT-5的密度ρ=7 600 kg/m3，泊松比为0.32，刚度系数矩阵：

PZT压电系数矩阵：

PZT介电常数矩阵：

除压电层材料外，作为弹性层的紫铜材料参数如表1所示。

表1 弹性基片材料参数

压电振动能量发电装置的三维有限元模型如图3所示。上层为均匀分布的5个矩形压电陶瓷片，下层为带有凹槽的铜质弹性基板。其中悬臂梁结构右端固定，左端为自由状态，采用自由网格划分方法来划分网格。

图3 压电振动能量发电装置有限元模型

3.2 压电发电装置的模态分析

振动模态是弹性体结构固有的、整体的特性。通过对压电振动能量发电装置进行模态分析，探究其各阶固有频率及其对应的不同振型。当压电振动能量发电装置的固有频率与外加振源频率接近时，将会产生共振，产生较大的振幅，压电陶瓷上的应变更大，从而能够收集到更多的电能。

利用模态分析来确定所设计的能量发电装置的振动频率，若所得振动频率与环境中的固有振动频率相差甚远，则调整结构的相关参数，使其值尽量接近，从而使发电装置能够最大程度地利用生活环境中产生的振动能。通过对压电振动能量发电装置进行模态分析，得到系统未经过优化的前4阶固有频率及模态振型，如图4～图7所示。获得的各阶振型对应的固有频率如表2所示。

表2 优化前发电装置前4阶固有频率

图4 第1阶共振振型

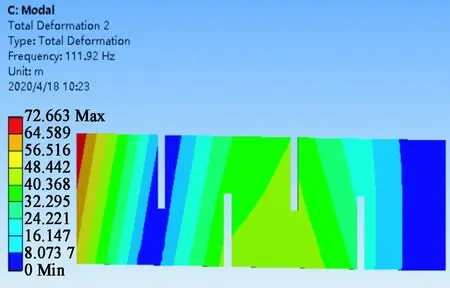
图5 第2阶共振振型

图6 第3阶共振振型

图7 第4阶共振振型

环境中的振动大多以低频为主，因此需要通过结构上的优化设计来降低结构的各阶固有频率。

3.3 压电陶瓷长度对发电装置性能的影响

压电振动能量发电装置的弹性基板尺寸长为50 mm、宽为16 mm、厚为0.1 mm，压电陶瓷片的宽度为4 mm、厚度为0.25 mm。采用控制变量法使得压电陶瓷片的长度分别为6 mm、8 mm、10 mm、12 mm、14 mm，在Workbench15.0中建立不同长度压电陶瓷对应的发电装置的有限元模型，如图8所示。

(a)L=6 mm

各个尺寸的悬臂梁均右端面固定，左端自由端面输入1 N集中力载荷。分别进行静力学分析，得到压电陶瓷片的最大应力和应变结果如表3所示。

表3 应力和应变随压电陶瓷长度变化表

由于发电装置输出的电能与压电陶瓷的应力、应变成正比，因此需尽可能提高压电陶瓷片的应力和应变。压电陶瓷片的最大应力和最大应变随压电陶瓷片长度变化的关系如图9、图10所示。

图9 最大应力随压电陶瓷片长度变化关系图

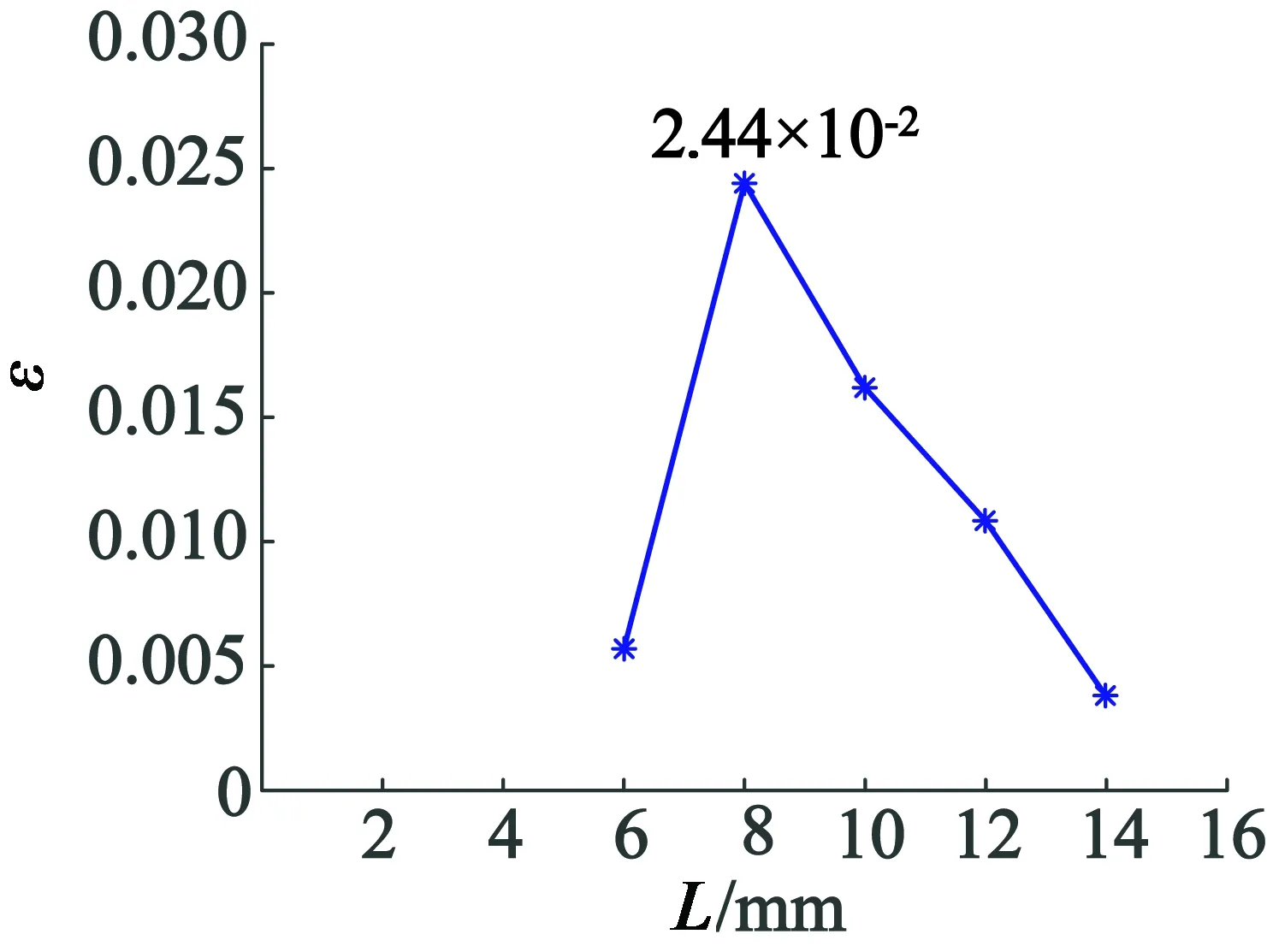
图10 最大应变随压电陶瓷片长度变化关系图

压电陶瓷受到的最大应力和最大应变，随着压电陶瓷片长度的增加先增大后减小。当压电陶瓷片长度为8 mm时，压电陶瓷产生的应力和应变最大，分别为1 579 MPa，应变为2.44×10-2，此时压电陶瓷片输出的电荷最多。

3.4 压电陶瓷厚度对采集器输出特性的影响

压电振动能量发电装置的弹性基板长为50 mm、宽为16 mm、厚为0.1 mm，固定压电陶瓷片的宽度为4 mm、长度为8 mm。采用控制变量法，使压电陶瓷片的厚度分别为0.15 mm、0.20 mm、0.25 mm、0.30 mm、0.35 mm。悬臂梁均右端面固定，左端自由端面输入1 N集中力载荷。进行静力学分析，得到分析结果数据如表4所示。

表4 应力和应变随压电陶瓷厚度变化表

分别绘制最大应力和最大应变随压电陶瓷片厚度变化的关系图，如图11、图12所示。

图11 最大应力随压电陶瓷片厚度变化关系图

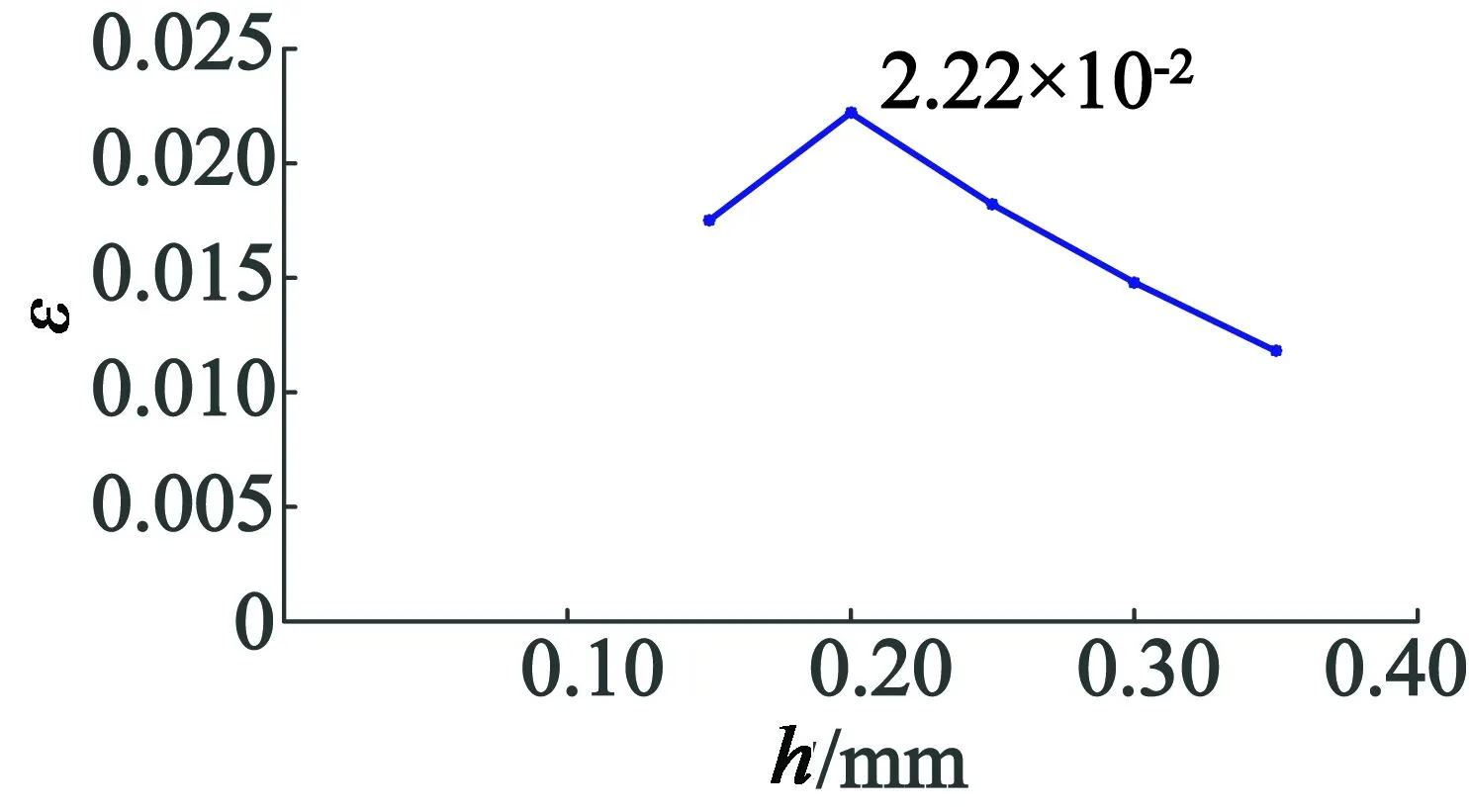
图12 最大应变随压电陶瓷片厚度变化关系图

由图11、图12可知，压电陶瓷的最大应力和最大应变,随着压电陶瓷片厚度的增加先增大而后减小。在所建立的模型中，当压电陶瓷片的厚度为0.2 mm时，压电陶瓷受到的最大应力为1 335 MPa，最大应变为2.22×10-2，此时压电陶瓷产生的形变最大，输出的电荷也最多。

3.5 弹性基板厚度对发电装置性能的影响

压电振动能量发电装置的压电陶瓷的长为8 mm、宽度为4 mm、厚为0.2 mm。弹性基板长为50 mm、宽为16 mm，采用控制变量法，使弹性基板的厚度分别为0.05 mm、0.10 mm、0.15 mm、0.20 mm、0.25 mm。各个模型的悬臂梁均右端面固定，左端自由端面输入1 N集中力载荷。进行静力学分析，获得分析结果数据如表5所示。

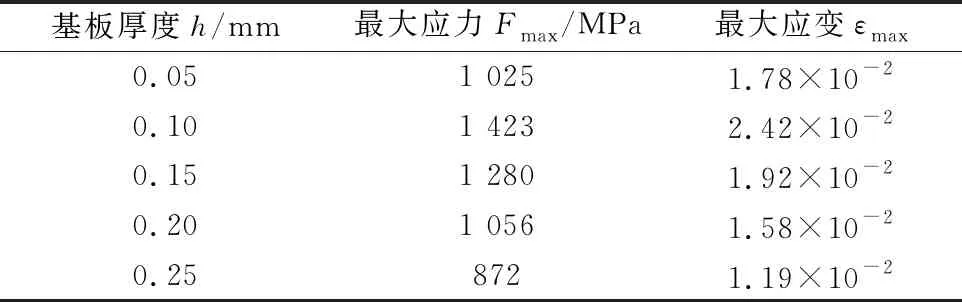
表5 应力和应变随弹性基板厚度变化表

根据分析结果，分别绘制最大应力和最大应变随弹性基板厚度变化的关系图，如图13、图14所示。

由图13、图14可知，压电陶瓷受到的最大应力和最大应变,随着弹性基板厚度的增加而先增大后减小，当弹性基板厚度为0.1 mm时，压电陶瓷受到的最大应力为1 423 MPa，最大应变为2.42×10-2。

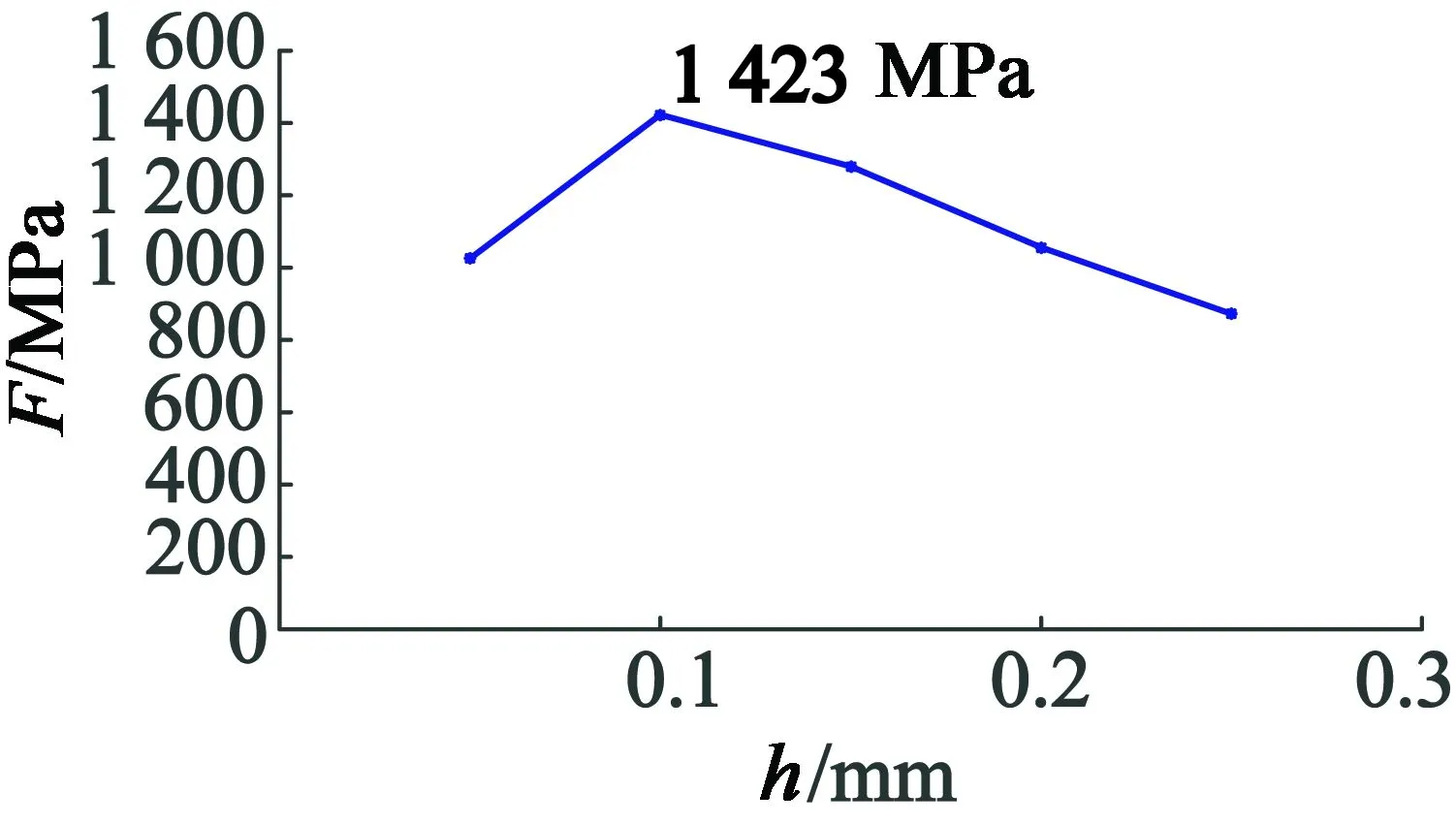
图13 最大应力随弹性基板厚度变化关系图

图14 最大应变随弹性基板厚度变化关系图

3.6 压电发电装置的优化

优化后的压电振动能量发电装置的结构参数是：压电陶瓷的长为8 mm、宽为4 mm、厚为0.2 mm。弹性基板的长为50 mm、宽为16 mm、厚为0.1 mm。对优化前的压电振动能量发电装置进行静力学分析，压电陶瓷上受到的最大应力和最大应变如图15、图16所示。

图15 优化前的最大应力图

图16 优化前的最大应变图

对优化后的压电振动能量发电装置进行与优化前同等条件下的静力学分析。压电陶瓷上受到的最大应力和最大应变如图17、图18所示。

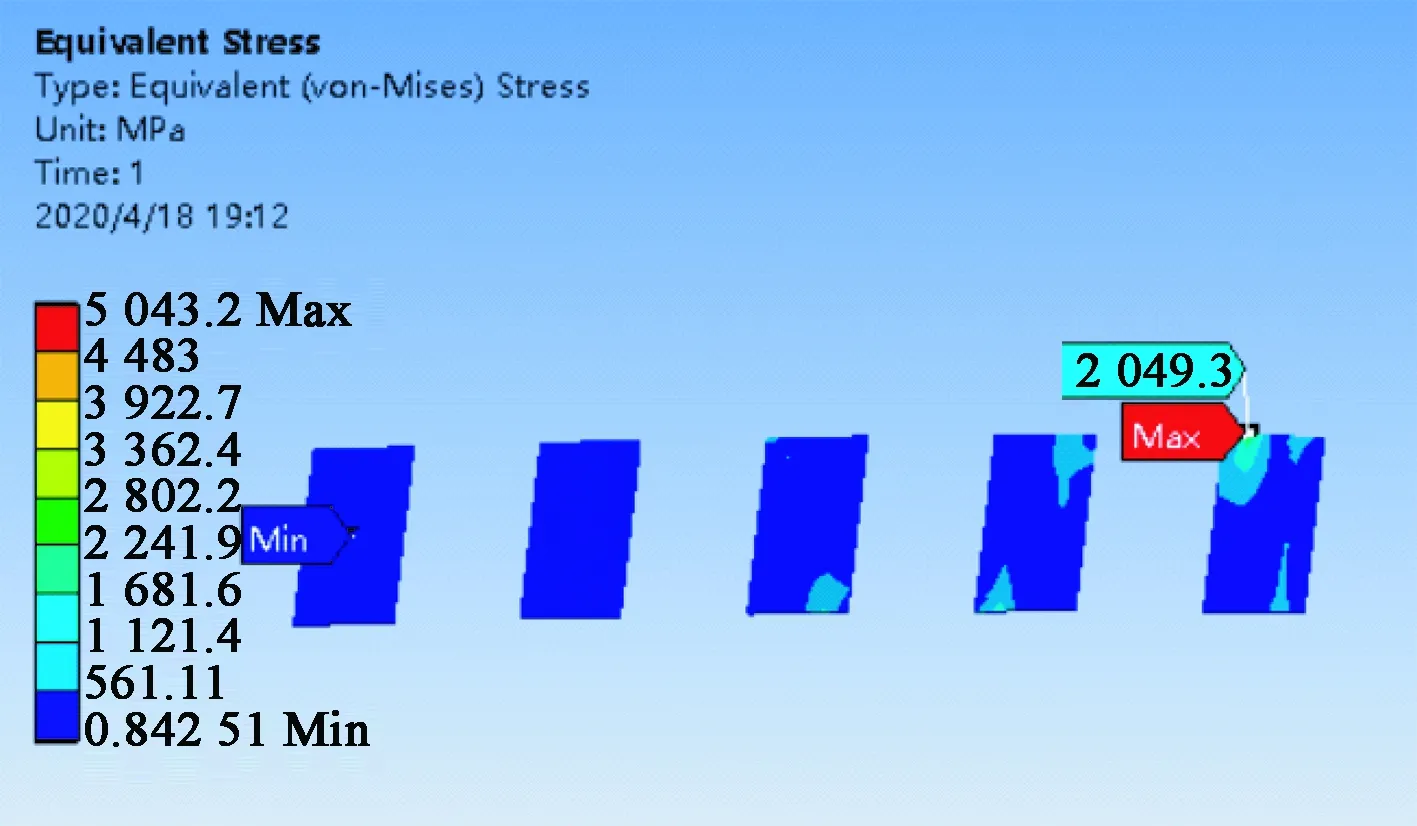
图17 优化后的最大应力图

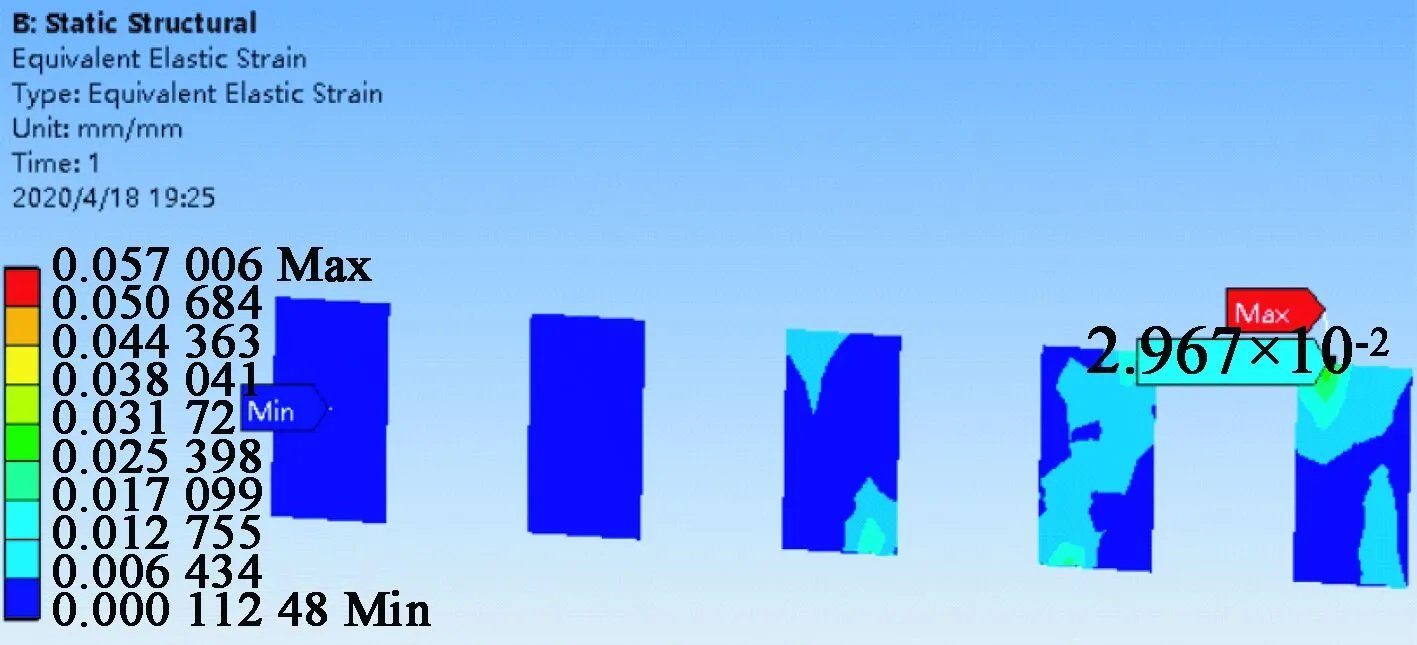
图18 优化后的最大应变图

优化前发电装置的压电陶瓷上的最大应力为1 041.4 MPa，优化后的最大应力为2 049.3 MPa；优化前能量采集器的最大应变为1.083×10-2，优化后的压电陶瓷的最大应变为2.967×10-2。优化后的压电陶瓷的最大应力和最大应变都有了较大的提高。

对优化后的发电装置进行与优化前同等条件下的模态分析，得到的第1阶固有频率如图19所示，前4阶固有频率如表6所示。

表6 优化后发电装置前4阶固有频率

图19 优化后的第1阶固有频率

通过对比优化前后前4阶固有频率，优化后的频率相比优化前有了较大的降低，能满足环境中的多种低频下的激励共振。

4 结 语

本文设计了一款多槽型压电振动能量发电装置，通过开槽可增加压电元件的应力和应变，进而增强其发电能力。利用有限元方法建立了其分析模型，并进行了静力学和模态仿真分析。采用控制变量法对压电发电装置进行分析，改变压电陶瓷的长度、厚度和弹性基体厚度等变量，获得设计参数对压电元件应力和应变的影响规律，并在此基础上对微型压电振动能量发电装置进行优化。