基于分形理论的矿粉粒度粒形对成球抗压强度的影响研究
陈 韧,康庆国,黄 妍,4,刘 研,张作良,赵世禹,高明辉,杨 帆
(1. 辽宁科技学院,辽宁 本溪 117004;2. 辽宁省低品位非伴生铁矿优化应用重点实验室,辽宁 本溪 117004;3. 五矿营口中板有限责任公司炼铁厂,辽宁 营口 115000;4东北大学 冶金学院,辽宁 沈阳 110819)
0 前言
矿粉的成球性及生球抗压强度是球团造球过程中的重要性能参数,测定并改善矿粉的成球性,提高生球抗压强度对球团造球生产工艺具有重要意义。目前对矿粉造球过程的研究主要集中在对原料天然性质、湿度、添加剂成分以及造球工艺条件等〔1〕,这些研究仍属于宏观的研究范畴,并没有考虑粒度分布、颗粒形态等微观机制对其成球性的影响。在诸如矿粉一类粉体颗粒群研究中,粒度分布、颗粒粒形是其重要的特征值,它们常常决定着粉体的物理、力学和化学性质。因此,科学地测试评价矿粉的粒度分布、颗粒粒形等特征值对深入研究矿粉的作用机制是十分必要的。
1 实验
1.1 矿粉粒度与粒形测定
选取5种营口五矿炼铁厂所使用的不同成分精矿粉,进行粒度分布、粒形及比表面积测定,矿粉化学成分如表1所示。对矿粉进行超声分散后采用激光动态图像粒度粒形分析系统测定矿粉粒度及粒形分布,并对每组矿粉拍摄5000组粒形图像,得到矿粉粒度分布如表2所示。得到的矿粉粒形如图1所示。
1.2 矿粉成球性及生球强度测定
首先采用M.A.尼契波连柯“自由滴”法对矿粉成球直径进行测定〔2-3〕,具体实验步骤如图2所示,取其10个生球的抗压强度的平均值进行评价,测定结果如表3所示。
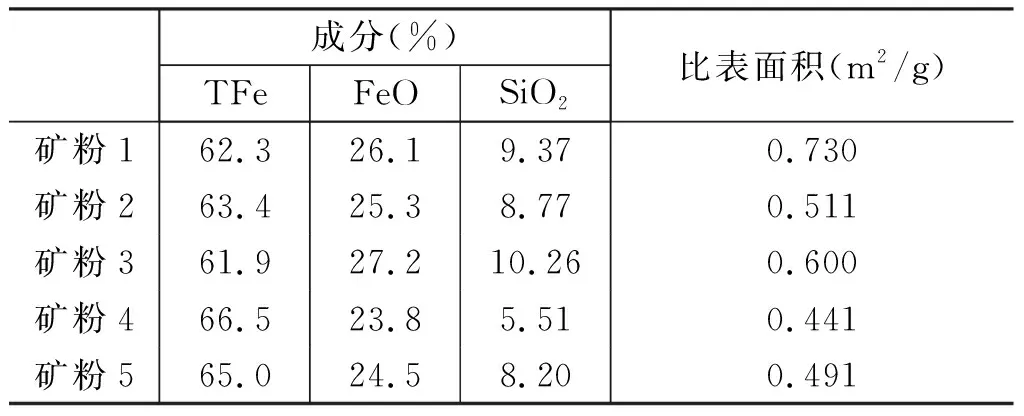
表1 矿粉化学成分及比表面积

表2 矿粉粒度分布

表3 不同矿粉的成球性及抗压强度

图1 矿粉粒形

图2 实验步骤
1.3 计算与分析
1.3.1 矿粉粒度分布的分维数计算
Mandlbrat认为〔4-6〕:分散颗粒系统粒度分布如果具有分形特性,则有:
N(>x)=C·x-D
(1)
式中:N(>x)为分散颗粒系统中粒度大于某一尺寸x的颗粒数目;x为某一颗粒的粒度;D为分布分维数;C为常数。
基于重整化群概念分析矿粉产生过程,假设原始矿粉为边长为L的立方体共N0个,称每一个立方体为0级原胞,并做假设每个0级原胞可分裂为8个边长为L/2的与原胞完全相似的0级单元。如果分裂持续下去,则每次分裂的概率为f,则上述分裂问题即被重整化群,则第n级元胞的体积为:
(2)
分裂至n级原胞的数目为:
Nna=(8f)n(1-f)N0=(8f)nN0a
(3)
式中:Nna=(1-f)N0是没有发生分裂的0级原胞的数目。将式(2)、(3)两边取对数,并消去n得:
(4)
因为分裂的线性尺寸x可写成:
xn~Vn1/3
(5)
式(4)可改写成:
Nna(>xn)=C0xn-31n8f/1n8
(6)
式中:C0是与分裂有关的常数。则式(6)满足式(1),其分维数为:
(7)
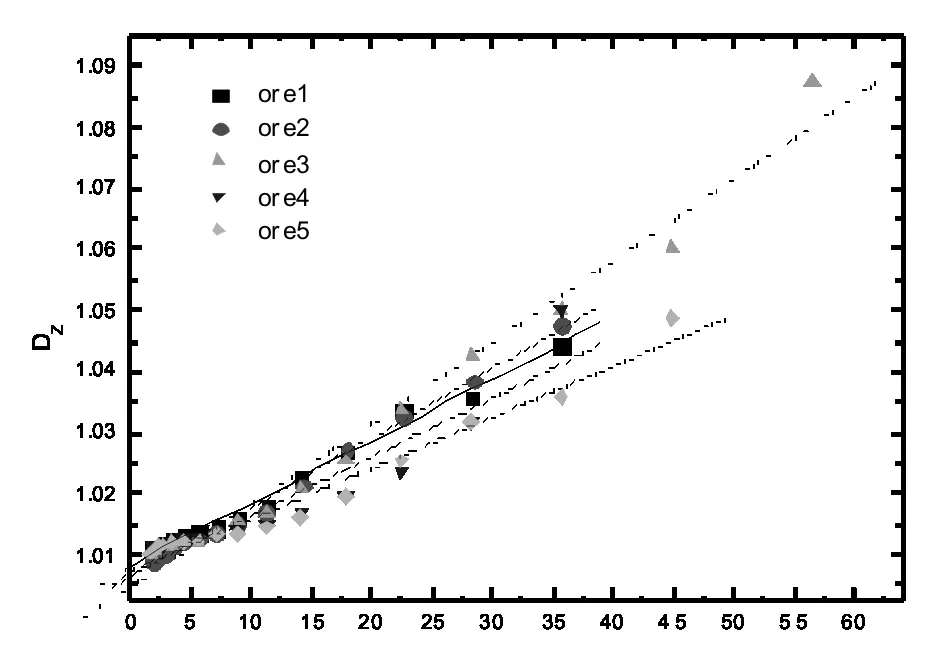
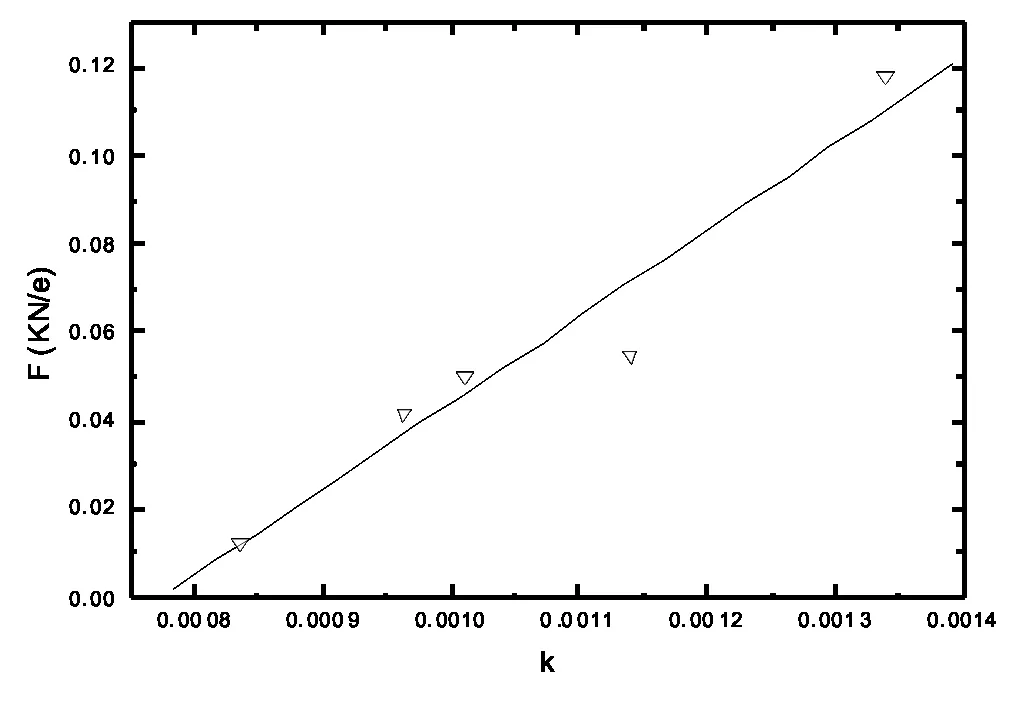
上式表明:在标度不变的分裂过程中将产生分形分布。这个模型把分裂概率f与分维数D相关,其中1/8 0 (8) 假设M0为矿粉颗粒的总数目,x为颗粒某一粒级粒径,则M(x)称做小于等于粒径x的颗粒总数。假设下式关系成立: (9) 则该矿粉颗粒系统满足分形特性,D为分布分维数。 定义颗粒群的颗粒累积分布函数F(x)、体积积累分布函数v(x)分别为: (10) (11) 对式(11)进行微分运算: (12) 而dV(x)=kx3N0dF(x),k为系数。为求得dF(x),对式(10)进行微分运算: (13) 故dv(x)可表示为: (14) 对式(14)进行积分运算,并给出一组边界条件: v(xmin)=0;v(xmin)=1 (15) 由此,确定粒径x与累计体积v(x)的关系表达式为: (16) 一般xmin≪xmax,故式(16)转化为: (17) 对式(17)两边取对数可得: 1nv(x)=(3-D)1n(x/xmax) (18) 由式(18),以1n(x/xmax)为横坐标,1n(V(x)/V0)为纵坐标,在双对数坐标系内画出对应的散点图并线性拟合各数据点,得到拟合直线Y=B+AX,(3-A)即为粒度分布分形维数D。5种矿粉粒度分布分维数计算结果如表4所示。 表4 不同矿粉粒度分布分维数 矿粉粒度分布分维数D与矿粉比表面积及成球性间关系如图3所示,矿粉粒度分布分维数D随矿粉比表面积A变大而增大,自由滴实验成球直径增大。即矿粉粒度越细其复杂程度越大,分布分维数越大,成球性越好。 图3 分布分维数D与比表面积A及成球性φ关系 1.3.2 矿粉颗粒边界织构分维数的计算 分形理论认为众多自然边界可以是统计自相似的而不必严格自相似。其含义是:虽然任一部分的放大结构并不严格自相似,但边界上的任何部分和其它部分看起来都是相似的。因此可以把单个矿粉颗粒看作是以曲折“海岸线”为边界的岛屿,由分形体的分类〔6-8〕:分维数作为图形的外部特征,即聚集体总体构造的表征,被定义为构造分形,而聚集体的断面的织构特征可用从边界上抽取出来的曲线表示,这种用于描述聚集体织构的分维数定义为织构分形。由此可见,矿粉颗粒断面的曲折边界属于织构分形的研究范畴。 由实验得到的矿粉颗粒边界在图像放大过程,码尺的最小单位为0.3527×0.3527mm2/pixel。低于这一值时,矿粉颗粒边界将明显具有欧氏几何边界的特点〔9〕。 测量矿粉颗粒边界的码尺为ε(实验中以pixel为单位),覆盖图像中全部边界的码数为N(ε),有 N(ε)∝ε-DZ (19) 这样由矿粉颗粒边界长度L(ε)=N(ε)·ε就可得到: L(ε)∝ε1-DZ (20) 因此,改变ε的大小得到一组ε-L(ε)值,将L(ε)或N(ε)与ε绘制在双对数坐标上,利用线性回归方法确定的直线斜率即为织构分维数DZ。图像处理过程如图4所示,其中ε为码尺,曲线部分为矿粉颗粒边界。 原始图像 提取边界 码尺为覆盖 按上述处理方法编制计算机程序,对每组矿粉所拍摄5000组粒形图像分别进行织构分维数计算,并根其据粒度大小及各粒度所占百分比对得到的织构分维数Z进行加权平均〔9〕。得到的5种矿粉各粒度级别颗粒的织构分维数如图5所示。由图5,矿粉颗粒的织构分维数随矿粉颗粒级别的增大而增加,对于不同矿粉而言,在小粒度级别(0~10μm)范围内,其织构分维数差别不明显,而随着粒度级别的提高(>10μm),矿粉颗粒织构分维数明显不同,这种差别可能是由于不同的选矿工艺造成的。 Φ(μm) 1.3.3 生球抗压强度与颗粒织构分维数关系 对5种矿粉颗粒粒径与颗粒织构分维数实验数据进行回归分析,如图5所示,得到如表5所示回归关系。 表5 不同矿粉织构分维数回归关系 回归关系式中斜率K越大则表明在同粒度级别下矿粉颗粒群中的颗粒边界更复杂,即矿粉越粗糙,这显然与矿粉的化学成分及选矿工艺有关。因此,可将K定义为与选矿工艺和化学成分有关的织构特征参数。将K值与成球强度相关联,如图6所示。K值越小则成球强度越低,表明同粒度级别的矿粉颗粒越光滑,颗粒间摩擦力小,生球强度低。 图6 K与生球抗压强度间的关系 (1)分形理论可用于表征矿粉颗粒及颗粒群,矿粉颗粒群具有自相似特征,其分形特征可表征矿粉颗粒群的复杂程度。 (2)矿粉的成球性与矿粉粒度分布分维数有关,分维数越大,比表面积越大,其复杂程度越大,矿粉成球性越好。 (3)矿粉的生球抗压强度与矿粉颗粒的边界分维数有关,其织构分维数越大,对于小粒径矿粉颗粒(0-10μm)织构分维数无明显差别,而对于大颗粒矿粉其织构分维数差别较大,与选矿工艺有关。 (4)同粒度级别的矿粉颗粒,其分形特征参数K越小,则颗粒表面越光滑,颗粒间摩擦力越小,成球强度越低。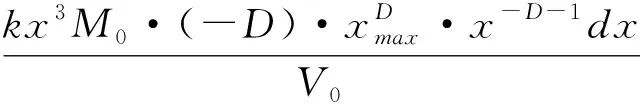




2 结论

