高温高压柔性介质成形GH4169异形超细曲面的致密化行为

马丁，郎利辉，肖毅，孟凡迪，李世越

高温高压柔性介质成形GH4169异形超细曲面的致密化行为

马丁，郎利辉，肖毅，孟凡迪，李世越

(北京航空航天大学 机械工程及自动化学院，北京 100083)

采用陶瓷模具控形，在高温高压柔性介质加载下制备GH4169异形超细曲面，曲面厚度为0.6 mm。利用扫描电镜观察和分析异形曲面横截面的致密化程度，结果表明，截面两端处最致密，中部中心处次之，中部边缘处致密度化程度最低。同时采用经过单拉实验修正后的Shima-Oyane本构方程进行数值模拟，得到异形曲面中性面的致密度、等效柯西应力与位移矢量三者的分布云图，并从节点位移角度阐述GH4169粉末在刚性模具中的致密化行为。结果表明，热等静压过程中，异形曲面沿厚度方向向内收缩，两端的位移最大，致密度最高，中部的中心位置次之，中部边缘处致密度最低。模拟结果与实验结果一致。

陶瓷模具；柔性介质；热等静压；超细曲面；数值模拟；致密度；节点位移

GH4169合金凭借其良好的高温力学性能，广泛应用于航空航天领域。但GH4169合金存在加工困难，材料利用率低等问题，亟需开发出低成本、高可靠性的成形工艺[1]。热等静压(hot isostatic pressing, HIP)为典型的高温高压柔性介质成形，是在玻璃或金属包套内填充金属粉末，然后放入热等静压炉内，以惰性气体为柔性传力介质，压力均匀等值地作用在包套外表面，完成包套内粉末的致密化。由于粉末的流动性，热等静压技术在成形内部难加工特征的零部件方面具有巨大优势。借助内部模具控形的热等静压技术由于其近净成形的特性，对于成形复杂结构的GH4169具有很大优势。其不仅可以近净成形难加工零件，还能克服精铸中常出现的充不满、大偏析等问题。热等静压使用的模具材料一般为石墨、45号钢等，在高温高压的成形环境下，模具出现变形、扩散的情况。随着陶瓷3D打印技术的发展，奥地利Lithoz公司的LCM (Lithography-based ceramic manufacturing，基于光刻的陶瓷制造)技术可以在无模具的情况下制备高复杂结构的陶瓷模具。热等静压技术采用3D打印成形的陶瓷模具，可便捷高效地成形高复杂度的内部曲面结 构[2]。陶瓷模具在高温下具有良好的抗变形能力，后续加工时也可采用脱芯腐设备彻底去除模具。因此本文作者利用内部陶瓷模具控形，通过热等静压来成形异形超细曲面。

金属粉末在高温高压柔性介质下的致密化过程分为3个阶段：粉末受压流动，相互靠近重新排列；粉末相互挤压塑性变形，形成连接孔隙；蠕变闭合孔隙，界面扩散消除颗粒原始边界(prior particle boundary，PPB)[3]。由于各阶段复杂且相互影响，实现最终成形情况的准确预测十分困难。研究表明[4]，采用数值模拟可准确预测粉末最终的收缩情况与致密度分布，但目前很少有人对模具内部的粉末致密化情况与规律进行数值模拟研究。对于复杂小特征来说，由于陶瓷模具的存在，高温高压柔性介质加载初期粉末的流动性与粉末受力情况较复杂[5]，力的衰减难以确定，因而难以预测最终的成形情况。现阶段，金属粉末热等静压致密化过程的数值模拟研究多采用MSC.Marc内置的Shima-Oyane本构模型[6−7]，经过单轴拉伸实验修正后，可较准确地预测粉末流动变形行为[8−10]。通过以上模拟手段，已实现对热等静压过程中的粉体形状变化和致密度分布的准确预测，对理解金属粉末在高温高压柔性介质成形中的致密化过程有一定的指导作用。而对于某些由内部模具保证的细小内部特征，除压制力外，粉体与模具之间还存在摩擦力，在此种更复杂的热力耦合条件下，粉末在模具内的致密化规律尚不明确。本文作者以GH4169粉末填充陶瓷模具内的超细异形曲面缝，在高温高压柔性介质加载下完成异形曲面的致密化，利用扫描电镜观察和分析曲面不同位置的致密化程度，并结合数值模拟异形曲面横截面上不同节点的位移与节点位移矢量图，研究粉体在刚性模具内的致密化行为规律，对研究高温高压柔性介质成形GH4169超细曲面异形结构的致密化规律有指导意义。

1 实验与模拟

1.1 热等静压成形GH4169合金异形超细曲面

热等静压成形所用模具为3D打印成形的陶瓷模具，CAD(computer aided design，计算机辅助设计)模型如图1所示，模具厚度为5 mm，有宽度为0.6 mm的异形曲面缝，以成形超细曲面。所用原料粉末为旋转电极法制备的GH4169合金球形粉末，成分列于表1，粉末粒径为0~20 μm。由于GH4169的熔点较高，相应的热等静压工艺温度也较高，因此包套材料采用熔点为1375~1450℃的日本SUS不锈钢系列中的SUS316L，包套厚度为2 mm。

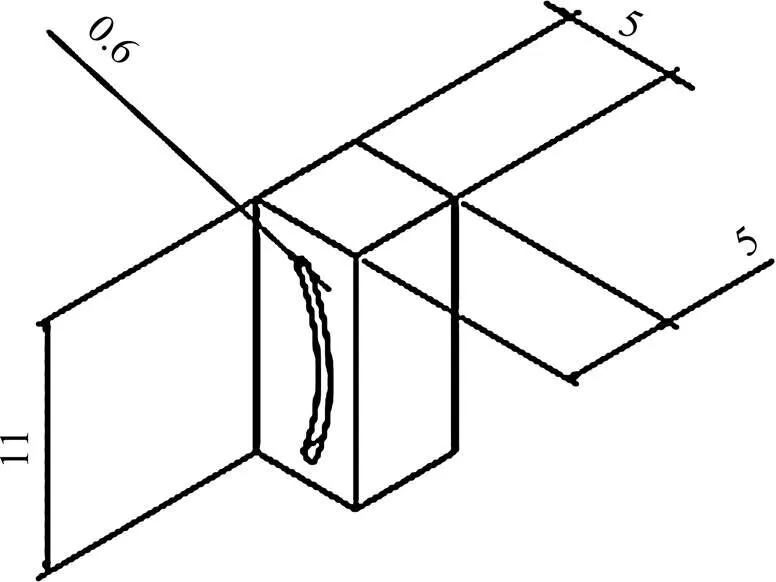
图1 热等静压成形GH4169合金异形超细曲面的陶瓷模具CAD模型

当采用热等静压(hot isostatic pressing，HIP)作为进一步致密化的手段时，最高压强一般为150 MPa[11]，最高温度为粉末材料熔点的80%[12−13]。图2所示为GH4169合金的热力学平衡相图[14]，由图可知GH4169合金在1 050 ℃时δ相完全固溶，在1 296 ℃时MC相完全固溶。超细异形曲面内粉末为单轴压缩，压力衰减大，粉末流动困难，原始颗粒边界(previous particle boundary, PPB)难以消除[15−16]，GH4169的PPB主要由MC相碳化物构成[17]。为尽可能消除PPB，在热等静压前对陶瓷模具内的GH4169合金粉末进行预热处理，预热温度为1 050 ℃。通过预热处理，使粉末颗粒表面偏析的MC相形成元素含量减少，同时在一定程度上消除粉末颗粒边界上的氧化物、碳化物质点数量，减少热等静压成形过程中颗粒边界上的形核点，从而抑制PPB的形成。图3所示为GH4169的热等静压工艺制度。为提高粉末流动性，先升温后升压，在1 050 ℃下预热2 h，之后1 h内升温升压至1 200 ℃和150 MPa，保温保压，完成致密化。为避免形成较多硬脆相(Laves相)，保温30 min时开始降温卸压。热等静压后去除包套，露出陶瓷模具表面，使用脱芯腐设备，加入腐蚀剂，在一定温度和压力下去除陶瓷模具，再经过机加工获得与基体连接在一起的GH4169合金异形曲面，如图4所示。

表1 GH4169粉末的化学成分

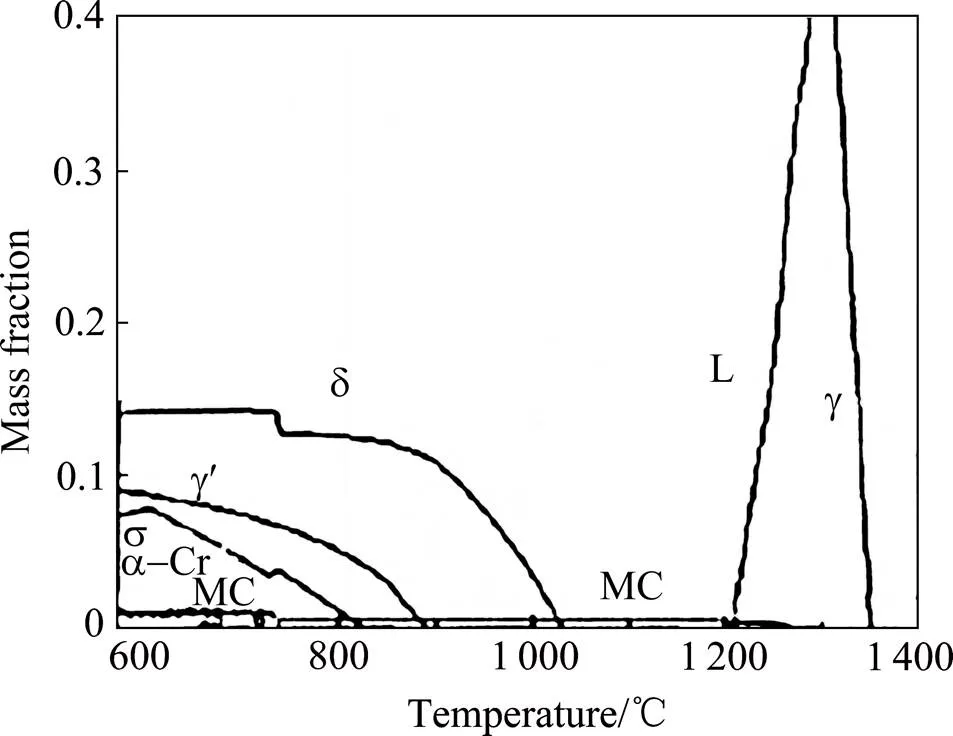
图2 GH4169合金的热力学平衡相图[14]

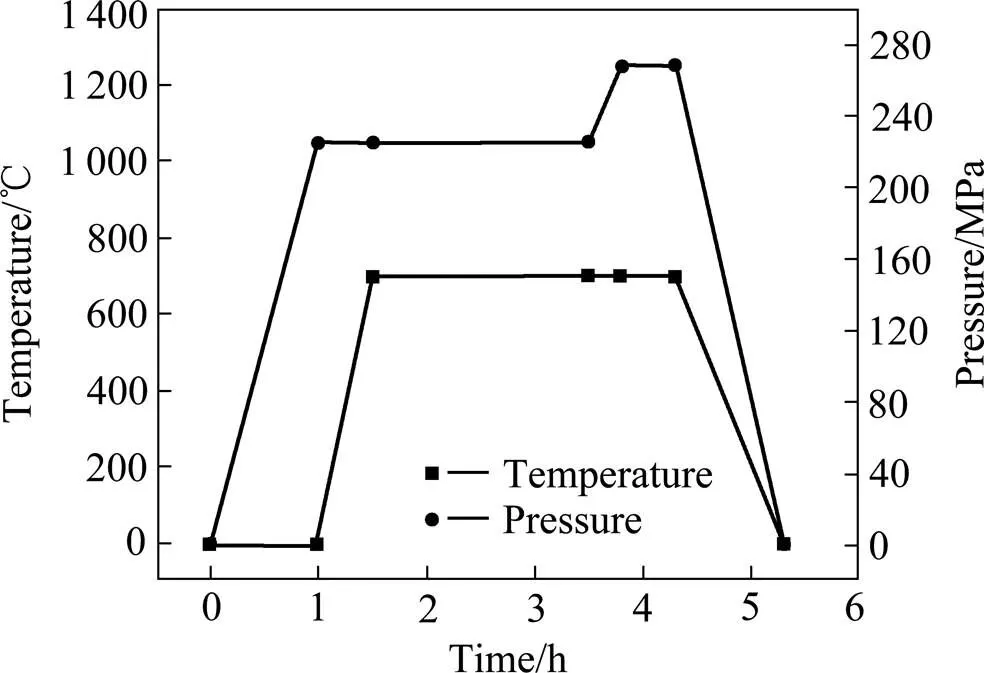
图3 热等静压工艺制度

图4 HIP成形的GH4169超细异形曲面

采用线切割从异形曲面上切下大小合适的试样，打磨、腐蚀后，用日本JEOL公司生产的JSM-6010型号的扫描电镜观察曲面的截面形貌，评估异形曲面的致密化情况。加速电压为20 kV。

1.2 模拟参数

采用经过单轴压缩试验修正过的Shima-Oyane屈服准则进行模拟，CAD模型如图5所示。为提高网格质量，防止网格畸变，采用Hypermesh软件对异形曲面划分六面体网格，如图6所示，网格数量为28 380个。陶瓷模具设置为刚体。

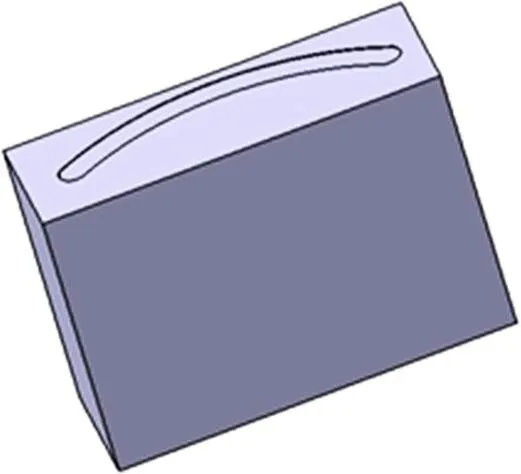
图5 数值模拟CAD模型

图6 超细异形曲面网格

粉末的HIP过程受复杂的热力耦合作用，是典型的非线性大变形问题，为提高运算速度，采用瞬态静力学的热力耦合，设定固定时间步长，收敛判据为相对残余力或相对位移，两者可自动转换。迭代方式为修正的牛顿−拉夫森方法，且不收敛继续计算。采用更新拉格朗日法对粉末HIP过程中的大应变进行描述。根据实际装粉量计算出粉体的初始致密度为0.65，材料参数为GH4169在不同温度下的力学性能参数。

2 结果与分析

2.1 异形曲面形貌

图7(a)所示为异形曲面的横截面SEM形貌，可见截面较光滑，无明显缺陷。两端边缘即图7(a)中的点1处形貌如图7(b)所示，致密度高，颗粒已相互靠近并重新排列，且产生较大塑性变形并发生扩散，无明显颗粒边界。在中部的边缘处(图7(a)中点2)可看到清晰的球形颗粒形貌，颗粒几乎未发生塑性变形，颗粒之间无明显接触，致密度较差(见图7(c)所示)。中部的中心处(图7(a)中的点3)形貌如图7(d)所示，可见该部位的致密度比中部边缘处的高，但不如两端边缘处致密，粉末颗粒已相互接触挤压且发生变形，边界处有一定扩散。

2.2 模拟结果与分析

对异形曲面进行数值模拟，在异形曲面取高度方向的中间截面，该面为无高度方向上位移的中性面。对异形曲面的中性面进行模拟研究，得到最后第600步、25 200 s时致密度的分布云图如图8所示。可见截面两端的致密度最高，中部的中心位置次之，中部边缘的密度最低，与图7所示实验结果基本一致。

在HIP的保温保压阶段，异形曲面横截面上的柯西等效应力分布云图如图9所示。图10所示为异形曲面截面的节点位移矢量图。对比图9和图8，可看出保温保压阶段的柯西等效应力分布与致密度分布相似，即等效应力越大的位置，粉末体致密度越高。结合图10可知，在柯西等效应力较大处，节点位移也较大，即网格的变形收缩大，故致密度较高。

从图10中位移矢量方向来看，绝大部分节点的移动方向指向中性面内部，因此异形曲面内部的致密度较大；从位移矢量大小来看，中性面的两端处位移矢量最大，因此两端处的致密度最高。

图7 GH4169异形曲面的截面SEM形貌

(a) SEM image of profiled surface; (b), (c), (d) SEM image of point 1, point 2 and point 3 in Fig.7(a), respectively

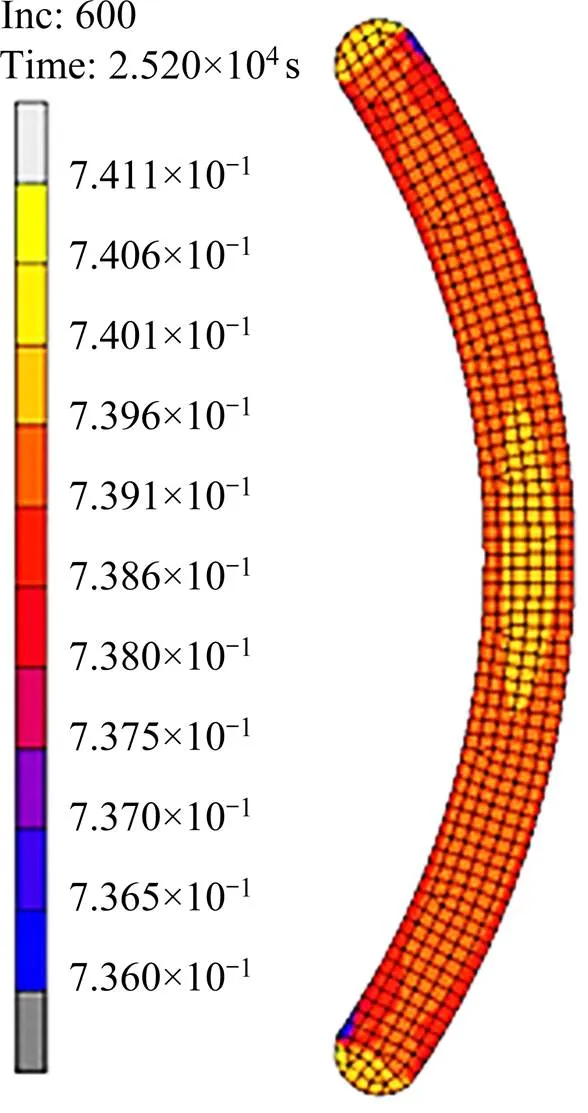
图8 异形曲面中性面的致密度分布云图

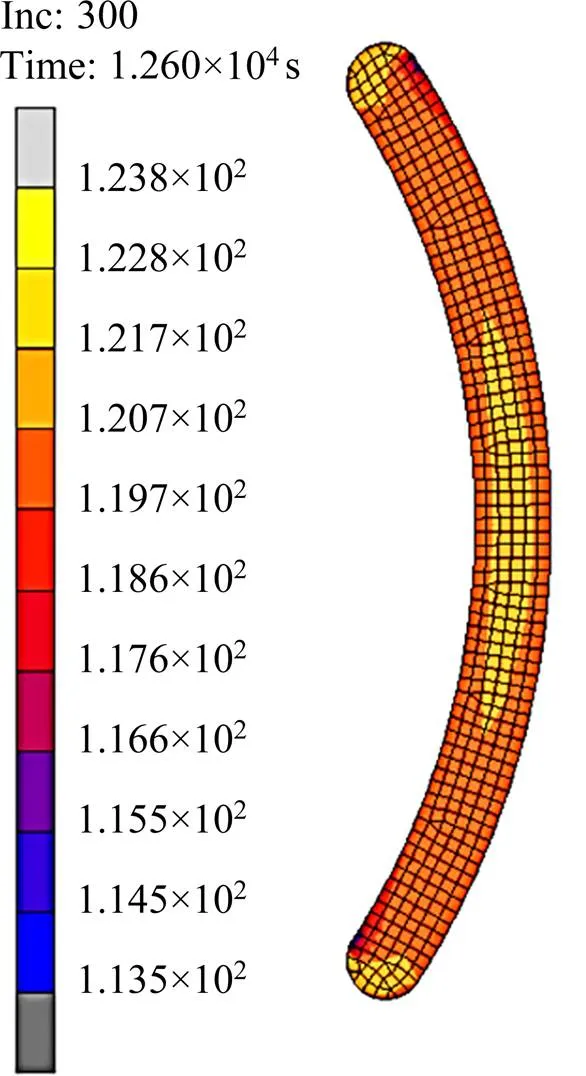
图9 保温保压阶段中性面的等效柯西应力分布云图

图11所示为热等静压过程中的升温升压和保温阶段，中性面上不同位置典型节点的位移变化。可见中性面上沿圆弧方向分布的节点4，3，2和1处的最终位移依次增大，在等效柯西应力作用下其位移不断叠加。中部边缘处的节点5的最终位移最小。

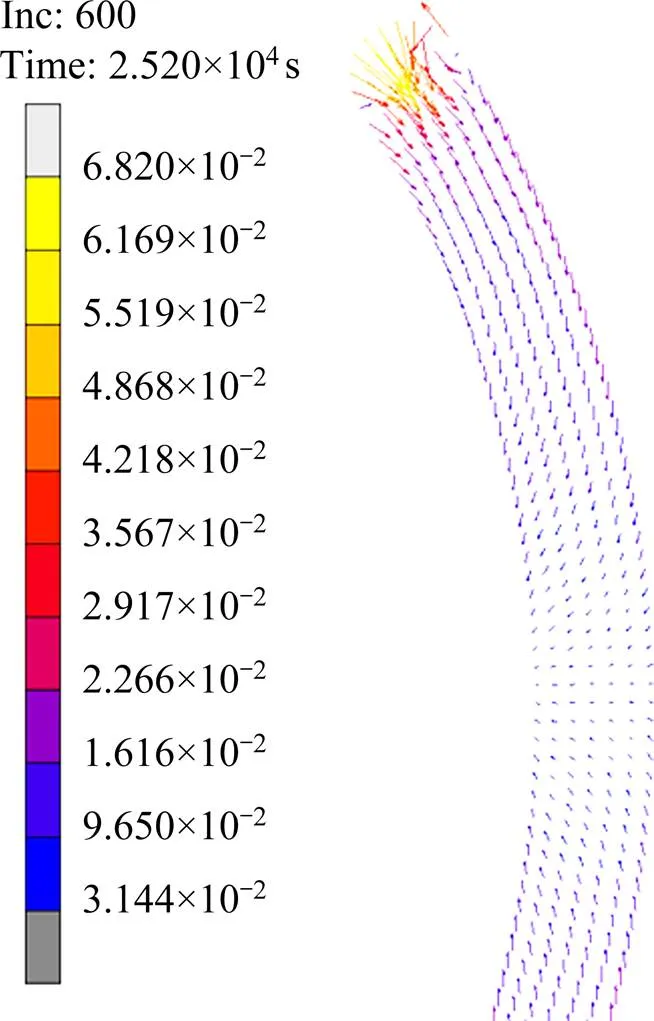
图10 异形曲面中性面节点的位移矢量图

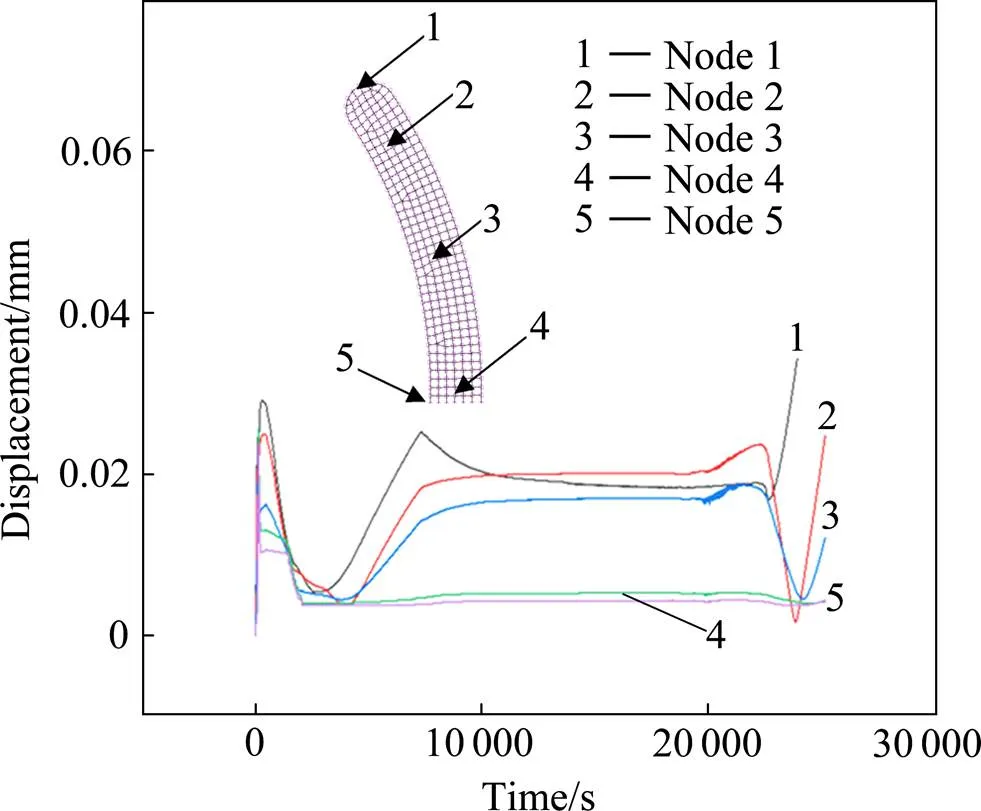
图11 异形曲面的中性面不同位置节点的位移

从图11看出，从1 050 ℃同时升温升压至1 200 ℃和150 MPa，升温升压时间为1 h。初期由于温度升高，单元膨胀，各节点产生正向位移且逐渐增大，越靠近两端处的节点正向位移越大。后期由于压力升高，单元受压抵消了热膨胀的影响而发生收缩，产生负向位移，节点的总位移减小。

保温保压阶段，各节点位移基本保持不变。初期，节点1发生收缩，位移减小；随着变形的继续，中性面上六面体八节点单元，除中性面上的节点4外，其他4个节点继续收缩，位移继续减小，而节点1处于两端最边缘处，故有少许扩张，正向位移增加，导致总位移减小，而其它节点继续收缩，产生的负向位移持续增大。

在降温卸压阶段，初期由于压力降低，除节点1外的其他各节点开始扩张，正向位移增加，总位移减小，而节点1由于外部有刚性模具，无法扩张，故无明显位移变化。降温卸压阶段后期，随温度降低，各节点收缩，继续产生负向位移，故负向位移持续增大。

在整个热等静压过程中，由于沿曲面圆弧方向向外，节点的位移不断增加，故靠近异形曲面两端处的节点1位移最大。而在异形曲面中心处附近，除节点3沿圆弧方向的收缩外，在厚度方向上靠外侧的节点也向内收缩，因此异形曲面中心有一部分区域致密度较高。

4 结论

1) 采用热等静压法制备GH4169合金异形超细曲面，用扫描电镜观察曲面的横截面，发现两端处最致密，中部的中心处次之，中部边缘处的致密度化程度最低。

2) 采用经过单拉实验修正后的Shima-Oyane本构方程进行数值模拟，结果表明，热等静压过程中，异形曲面向内收缩，中性面上的两端处位移最大，致密度最高，中部的中心位置次之，中部边缘处最低。模拟结果与实验结果一致。从节点位移角度阐述了 GH4169粉末在刚性模具中热等静压的致密化行为，符合实际情况。

[1] ZHANG C, YU L M, WANG H. Kinetic analysis for high-temperature coarsening of γ″ phase in Ni-based superalloy GH4169[J]. Materials (Basel, Switzerland), 2019, 12(13): 20− 25.

[2] XU H, HUANG Z C, HAN W, et al. Optimization of 3D printing model data of complex sculpture ceramic mold[C]// Advanced Science and Industry Research Cecter. Proceedings of 2017 2nd International Conference on Modelling, Simulation and Applied Mathematics (MSAM 2017), Bangkok, Thailand: Science and Engineering Research Center, 2017: 35−38.

[3] SEGURA I, MURR A L E, TERRAZAS C A, et al. Grain boundary and microstructure engineering of Inconel 690 cladding on stainless-steel 316L using electron-beam powder bed fusion additive manufacturing[J]. Journal of Materials Science & Technology, 2019, 35(2): 351−367.

[4] QIAN X, ZHOU J X, HAI N, et al. Effects of hot isostatic pressing temperature on casting shrinkage densification and microstructure of Ti6Al4V alloy[J]. China Foundry, 2017, 14(5): 429−434.

[5] 徐文才, 郎利辉, 黄西娜, 等. 铝合金复杂薄壁件热等静压成形数值模拟[J]. 锻压技术, 2019, 44(6): 65−72. XU Wencai, LANG Lihui, HUANG Xina, et al. Numerical simulation of hot isostatic pressing of aluminum alloy complex thin-walled parts[J]. Forging & Stamping Technology, 2019, 44(6): 65−72.

[6] SHIMA S, OYANEM. Plasticity theory for porous metals[J]. International Journal of Mechanical Sciences, 1976, 18(6): 285−291.

[7] Oyane M, Shima S, Kono Y. Theory of plasticity for porous metals[J]. Bulletin of the JSME, 1973, 16(99): 1254−1262.

[8] 瞿宗宏, 刘建涛, 张国星, 等. FGH4097合金热等静压成形数值模拟[J]. 材料热处理学报, 2017(7): 173−179. ZHAI Zonghong, LIU Jiantao, ZHANG Guoxing, et al. Numerical simulation of hot isostatic pressing of FGH4097 alloy[J]. Journal of Materials Heat Treatment, 2017(7): 173−179.

[9] GTEEN R J. A plasticity theory for porous solids[J]. International Journal of Mechanical Sciences, 1972, 14(4): 215− 224.

[10] RAO G A, SRINIVAS M, SARMA D S. Effect of oxygen content of powder on microstructure and mechanical properties of hot isostatically pressed superalloy Inconel 718[J]. Materials Science & Engineering A, 2006, 435: 84−79.

[11] JEONG Y Keun, NIIHARAK O. Microstructure and properties of alumina-silicon carbide nanocomposites fabricated by pressureless sintering and post hot-isostatic pressing[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(S1): 1−6.

[12] 张义文, 刘建涛. 粉末高温合金研究进展[J]. 中国材料进展, 2013(1): 11−12. ZHANG Yiwen, LIU Jiantao. Research progress of powder superalloys[J]. Progress in China Materials, 2013(1): 11−12.

[13] GAO Yang, ZHANG Dongyun, CAO Ming, et al. Effect of δ phase on high temperature mechanical performances of Inconel 718 fabricated with SLM process[J]. Materials Science & Engineering A, 2019, 767: 52−55

[14] SONG W D, HU M L, ZHANG H S, et al. Effects of different heat treatments on the dynamic shear response and shear localization in Inconel 718 alloy[J]. Materials Science & Engineering A, 2018, 725: 76−87.

[15] ZHENG X G, SHI Y N, LOU L H. Healing process of casting pores in a Ni-based superalloy by hot isostatic pressing[J]. Journal of Materials Science & Technology, 2015, 31(11): 1151−1157.

[16] CHANG L T, SUN W R, CUI Y Y, et al. Effect of heat treatment on microstructure and mechanicalproperties of the hotisostaticpressed Inconel 718 powder compact[J]. Journal of Alloys and Compounds, 2014, 590: 227−232.

[17] 赵丰, 姚草根, 范开春, 等. 粉末GH4169合金中的原始颗粒边界问题[J]. 宇航材料工艺, 2012, 42(1): 92−94.ZHAO Feng, YAO Caogen, FAN Kaichun, et al. The original particle boundary problem in powder GH4169 alloy[J]. Aerospace Materials Technology, 2012, 42(1): 92−94.

Densification behavior of GH4169 ultra-fine curved surface irregular structures formed by high temperature and high pressure flexible media

MA Ding, LANG Lihui, XIAO Yi, MENG Fandi, LI Shiyue

(School of Mechanical Engineering and Automation, Beihang University, Beijing 100083, China)

The ceramic mold was used to control the shape and the GH4169 ultra-fine irregular curved surface was prepared under the high temperature and high pressure flexible medium, the thickness of the curved surface was 0.5 mm. The densification degree of the irregular curved surface was observed and analyzed by SEM. The results show that the densification degree of the curved surface is the densest at both ends, followed by the middle center, and the lowest at the middle edge. At the same time, the Shima-Oyane constitutive equation modified by the uniaxial tension experiment was used to simulate the numerical simulation. The distribution nephogram of density, equivalent Cauchy stress and displacement vector of the neutral surface of the irregular curved surface were obtained. The densification behavior of GH4169 powder in the rigid mold was described from the point of node displacement. The results show that in the process of hot isostatic pressing, the irregular surface shrinks inward along the thickness direction. The displacement of the two ends is the largest, and the density is the highest. The center position in the middle is lower, and the edge in the middle is the lowest. The simulation results are consistent with the experimental results.

ceramic mold; flexible medium; hot isostatic pressing (HIP); ultra-fine curved surface; numerical simulation; density; node displacement

TF124

A

1673-0224(2020)03-185-06

2020−01−20；

2020−03−10

郎利辉，教授，博士。电话：010-82317062；E-mail: lang@buaa.edu.cn

(编辑 汤金芝)