船舶旋转角速度变化规律

吕锡宝

(青岛港引航站， 山东 青岛 266106)

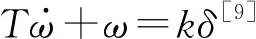
1 建立船舶旋转运动的特定场景

船舶在静止状态(v0=0，ω=0),艉部受艏艉方向的恒力F的作用，作加速旋转运动。水的阻尼力矩W随着船舶旋转角速度的提高而逐步增加，直至与F产生的动力矩达到平衡，此时ω达到最大，旋转加速度γ为零。若撤除横向旋转动力F,则船舶仅受水的阻尼力矩的作用，作旋转角速度衰减运动，角速度逐渐减小，水的阻尼力矩也随之减小，当ω为零时，水的阻尼力矩也为零，船舶处于非旋转状态。

针对船舶的整个旋转运动过程建立一个理想的运算场景，预设条件，以便从理论上进行推导计算：

1) 水面无风无流。

2) 作用力F的大小保持恒定，方向垂直于艏艉方向的中心线,作用于艉部端点。

3) 不考虑船舶旋转运动产生的附加质量以及旋转运动产生的船舶周围流场变化对船舶运动的影响。

4) 船舶为质量分布均匀的杠杆式船舶(长为L，宽为B，吃水为D，质量为m,重心为G)。

该理想船舶模型见图1。

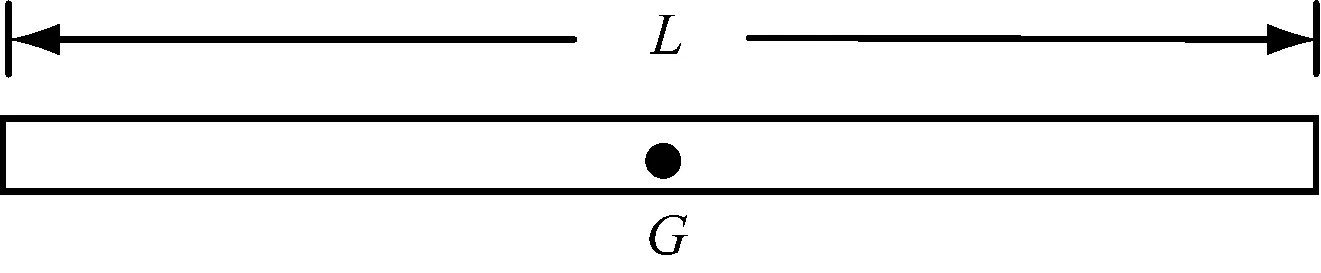
图1 理想船舶模型

2 ω的变化过程

2.1 ω的加速过程

船舶作旋转运动，水的阻力主要由垂直作用于舷侧的水动压力构成，水阻力在船舷侧的分布见图2,其中O为船舶转心。

根据伯努利定理，该力产生的力矩大小与ω2成正比(见图3)，因此W=M1+M2+M3=kω2。艉部所受动力产生的力矩为FL/2,见图4。根据旋转的定义，有关系

(1)

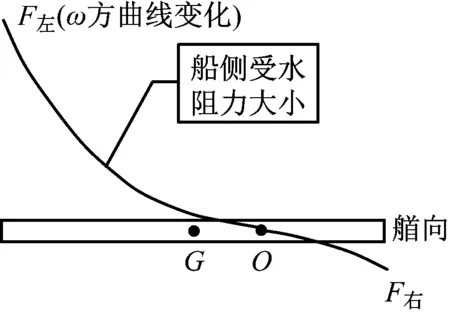
图2 船侧受水阻力

图3 舷侧受水的阻尼力矩

图4 艉部所受动力

式(1)中：I为船舶转动惯量；k水动力阻尼力矩系数。

FL/2-kω2=I(dω/dt)

(2)

dω/dt=FL/2I-k/I·ω2

(3)

令

FL/2I=α,k/I=b

(4)

则

dω/dt=a-bω2

(5)

dω/[1-(b/a)·ω2]=adt

(6)

令

β2=b/a

(7)

(8)

则

ln(1+βω)/(1-βω)=2βat+c

(9)

ω|t=0=0,c=0

(10)

1+βω=e2βat(1-βω)

(11)

(β+βe2βat)ω=e2βat-1

(12)

由此可得

(13)

式(1)～式(13)中:F为垂直作用于艉部的旋转动力；L为船长；t为船舶旋转时间；I为船舶转动惯量；k为水阻尼力矩系数。

根据式(13)可求出船舶旋转角速度加速过程中任一时刻t的即时ω。当t趋向于无穷大时，船舶的最大恒定旋转角速度为

(14)

(14)

2.2 ω衰减的过程

当撤除F时，船舶的运动仅受水阻尼力矩的作用，同理可根据旋转的定义列出关系式

(15)

式(15)中:ω0为旋转初始角速度；t为船舶旋转的时间。

根据式(15)可求出船舶在旋转角速度减小过程中任一时刻t的即时速度ω:当t=0时即初始时刻，ω|t=0=ω0；当t趋向于无穷大时，ω=0。

2.2.1ω衰减与时间的关系

对于某一特定的船舶，撤除F后，其ω的衰减按一定的规律进行，其大小随着时间t的增加逐渐减小。船的ω可根据式(15)表示为

ω=ω0[1/(kω0t/(I+1)]

(16)

ω/ω0=1/(kω0t/(I+1)

(17)

当ω1=ω0=1/2时，t1=I/kω0;当ω2/ω0=1/4时，t2=3I/kω0;当ω3/ω0=1/8时，t3=7I/kω0;当ωn/ω0=1/2n时，tn=(2n-1)I/kω0

每次速度衰减1/2所需的时间段为

(18)

根据式(18),ω每衰减1/2，所需时间比上一次要加倍。

2.2.2ω衰减与角度φ的关系

ω衰减1/2，在其衰减期Δt内，船舶的旋转角度φ是极为重要的要素，可判断安全旋转至目标航向所需的角度，提供准确的指导。根据角度φ、ω和t的关系，可列出关系式

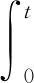
(19)

将式(15)代入式(19),可得

(20)

令

u=1/(kω0t/I+1)

(21)

则

t=(1/u-1)·I/kω0)

(22)

dt=-(I/kω0)·du/u2

(23)

(24)

当φ|t=0=0，C=0时,有

φ=I/k·ln(kω0t/I+1)

(25)

由式(25)可知:船舶速度衰减期间转过的角度也是时间的函数。设船舶撤除F时的旋转角速度为ω0,则ω降为1/2时，其φ为

(26)

由式(26)可得

Δφ1=Δφ2=Δφ3=…=I/k·ln2

(27)

由式(27)可知:ω值衰减1/2期间，船舶转过的角度是相等的。

2.3 水动力阻尼力矩系数k

在式(13)和式(15)中，除了水动力阻尼力矩系数,其他数据均为已知的，因此可把ω以时间t的函数来表达，对于某一排水量的特定船舶，k显然与船舶舷侧的水下的湿面积有关，即与船舶的长L、宽B和吃水d有关，可推导出k∝L2d,也可根据ω与t的关系求出该排水量对应的k值。

例如,某350 m集装箱船，吃水9 m，排水量为12万t，旋转角速度为20(°)/min时，停止横向动力距(如艏艉侧推器，正横顶推的拖船)，角速度降至10(°)/min所需时间为t，据此可求出船舶在吃水9 m时的水阻尼力矩常数k为

1/(kω0t/I+1)=ω/ω0=1/2

(28)

kω0t/I=1

(29)

k=I/ω0t(kg·m2/(°))

(30)

对于一艘特定的船舶，其惯性矩I为定值，ω0为定值，通过测定角速度减半所需的时间t，即可得出该船在某一特定吃水下的水阻尼力矩系数k。另外，在船舶旋转过程中，因为变加速旋转运动，水阻尼力的作用点有较小的移动，所以水阻尼力矩常数有微小的浮动，可忽略不计。

2.4 当船以一定的速度v运动时ω的变化规律

对于船舶在以一定的速度v运动(v0=v，ω=0)时，旋转规律是否一致,根据运动的相对原理，规律是完全一致的,只不过船舶静止时其重心围绕一个近似的点运动，运动时改变为围绕一个近似的圆运动，该圆的圆弧长度即为船舶重心驶过的距离。因此,运动中的船舶旋转也是适用该规律的(如航行中用舵转向)。

3 实际操船验证

在实际的操船实践中，选择在海况较好的情况下对船舶旋转规律进行实操验证。

大型油船和散矿船ROT(Rate of Turn)减半所需时间和角度分别见表1和表2,相关数据是在海面风力低于3级、平潮时的港内水域测得的，其中：表1所述大型油船长333 m,宽56 m，压载吃水9.5 m，载油吃水19.0 m;表2所述散矿船长300 m，宽50 m，压载吃水8.0 m，载货吃水16.11 m。

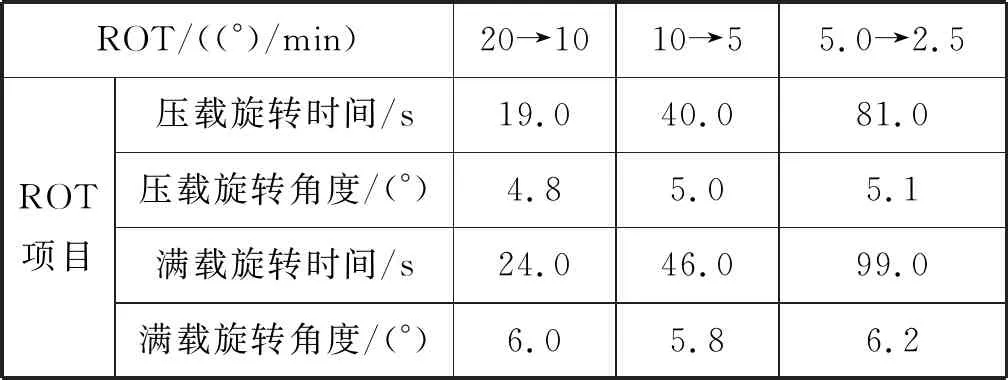
表1 大型油船ROT减半所需时间和角度

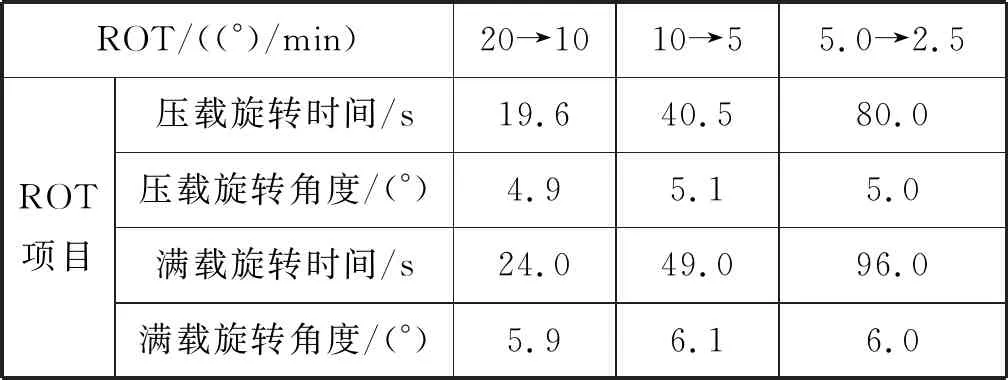
表2 大型散矿船ROT减半所需时间和角度

由表1和表2可知:对于某一特定船舶，ROT减半所需的时间是前一次的两倍，所转过的角度基本相同。通过实践进一步发现:宽长比相近的船舶，其旋转数据接近；不同的船舶吃水对应不同的方形系数，因此压载数据与满载数据有一定的差异。

4 结束语

根据多艘船舶的旋转实践和上述计算，可得出船舶旋转运动的结论:

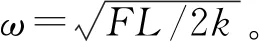
2) 船舶做减速旋转运动，无旋转动力矩，仅受水阻尼力矩的作用时，ω衰减1/2所转过的角度相等，即为Δφ=I/k·ln2,ω衰减1/2所需的t将越来越长，依顺序加倍,即Δtn=tn-tn-1=2n-1I/kω0。

3) 船舶的旋转数据与船舶长宽比L/B和船舶的吃水d有关，对于操船者而言，大多数常规船舶的ω衰减1/2在5°～6°,留出10°～12°的角度余量，让船舶旋转角速度ROT自然衰减，然后再用舵或其他(拖船，侧推器)手段把定航向是很容易实现的。大型油船和大型散矿船由于其旋转惯性矩太大，用舵或其他手段给出把定力矩相对较小，因此还要留出较大的角度余量，可留出约20°。

ω的变化规律在引航实践中具有重要的指导意义。虽然设定的条件在现实中不可能完全实现，但可在概念上给予明确指导，在受限水域转向、调头和避让中，精确把握旋转量的界限，即何时需要旋转加速，加到多大的量，何时需要旋转减速，抵近预定航向时的旋转角速度是多少，能否易于把握船舶航向等。在具体操作中，如果有数据支持，将有很重要的指导意义。操纵船舶不能绝对依赖反舵把定，必须留出适当的剩余角度使ω衰减，ω在船舶抵达预计航向时要小到易于把定，否则就需要加强拖船协助。这主要是考虑到船舶主机、舵机或船电故障等紧急情况下，船舶的旋转动态仍然可控。作为船舶的操纵者，引航员或船长需要在实践中积累船舶旋转的量的数据，按照上述规律依船舶类型、长度、船宽和吃水分类，将极大地提高船舶操作的安全性。

考虑到风流和浅水效应等的影响和特殊船型的独特性，必须给予每一次旋转操作适当的安全裕量，使得船舶的旋转运动在可控的误差范围内。作为操船者，需要认真总结经验，不断积累各类船型，各类装载状态船舶的旋转数据，把操作误差降到最低。