构造函数在高中数学解题中的应用

周晓琳

(江苏省南通市天星湖中学 226009)

一、概述构造函数法

类似于构造方程法，高中数学教学中函数知识与方程间联系紧密，合理应用构造函数法，利于培养并提高学生数学解题能力，特别是在几何与代数类型数学题干信息求解中有明显的适用性.数学题目实际求解过程中，将数学问题转换为形式简单的函数，以此简化求解过程，准确解答题目，为学生思维创造性发展创造条件.

数学解题过程中，要注意所构造的函数必须要满足以下内容：(1)函数与原题联系紧密.(2)创建的函数能够确保便于应用常规解题方法解答题目.(3)值域、单调性、奇偶性及周期性等方面，函数要符合题干要求，提高函数准确性.(4)根据题干条件构造函数.函数构造过程中，首先要全面分析命题条件、结论及特点，在提取其中逻辑与构想基础上，参考题目条件重新组合，一次获得满足解题要求的构造函数；此外还要观察并分析函数，联系分析条件与结论，最终获得正确结论.该解题方法逻辑性强，且解题方便，适用范围大，已成为高中数学解题中一种比较常见的解题方法.

二、高中数学解题中构造函数法的具体应用

1.利用构造函数比较式子大小

比如比较an与bn两个式子的大小.分析：通过观察这两个数可以看出，其有相同的指数但底数不同.因而，实际解题过程中，可通过构造幂函数y=xn，利用该函数单调性判断两个算式的大小.(1)如果n>0，在(-∞，+∞)区间范围内函数y=xn为单调递增，所以an与bn的大小取决于a与b的大小，即假若a>b，那么an>bn，反之则anb>0，那么anbn.

通过构造函数对比几个数的大小，是函数单调性应用的重要体现，此种情况下实际学习中，必须要了解构造函数的单调性，通过单调性对比函数大小.一般，构造函数是日常比较常用的初等函数或其复合形式，因此利用构造函数对比算式大小，了解一次、二次、指数、对数、幂函数及三角函数图象与单调性是非常重要的.

2.构造二次函数解答数学题

数学解题中，比如已知a、b、c∈R，且a+b+c=1，a2+b2+c2=1，求a的取值范围.

解答b+c=1-a，b2+c2=1-a2，那么构造函f(x)=2x2-2(b+c)x+b2+c2=(x-b)2+(x-c)2≥0是恒成立的，因此Δ=4(b+c)2-8(b2+c2)≤0，换言之4(1-a)2-8(1-a2)≤0，由此求出-1/3≤a≤1.

该题目解答过程中，将b+c与b2+c2视为一个整体，以此为二次函数f(x)=2x2-2(b+c)x+b2+c2的构造创造了条件，最后借助二次函数性质获求出最终结果.

3.构造函数应用于分解因式

比如分解因式a3+b3+c3-3abc.

该题目属于三元三次多项式，结构特殊且根与系数联系紧密，因而实际解题过程中，基于a、b、c三个单位构建三根三次多项式函数，利用函数求解问题.具体解题过程主要为：假设函数f(x)=(x-a)(x-b)(x-c)=x3+yx2+zx+r，得出a+b+c=-y，ab+ac+bc=z,abc=-r，获得以下三个公式：f(x)=a3+ya2+za+r=0，f(x)=b3+yb2+zb+r=0与f(x)=c3+yc2+zc+r=0.结合这三个等式，推导出(a3+b3+c3)+y(a2+b2+c2)+z(a+b+c)+3r=0，并求出最终结果，即a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-ac-bc).

4.构造一次函数解答数学题

解决以下问题时，可通过构造一次函数有效提高解题效率.假设不等式为2x-1>m(x2-1)，其满足|m|≤2的所有值条件下不等式恒成立，求未知数x取值范围.解答该类型题目是，首先可将不等式转换为(x2-1)m-(2x-1)<0，在此基础上构造一次函数即f(m)=(x2-1)m-(2x-1)(|m|≤2).然后结合该一次函数图象基本性质得到f(-2)<0，最后代入未知数x求出其最终取值范围.

5.构造可导函数

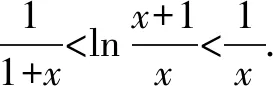
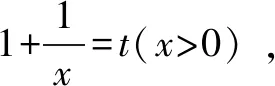
此过程中，采用换元法简化原不等式对数的真数部分，并构造两个可导函数，以此证明原不等式成立，其在不等式证明中应用比较广.

综上所述，随着新课标改革的深入推进，高中数学学科教学中，函数教学是非常重要的内容，应用构造函数法已成为解决数学问题的重要应用思想，对解题效率与学生解题能力的提高具有非常重要的意义.因此，高中学习阶段，老师要引导学生深入了解构造函数法解题思想应用的作用，了解函数性质及形式，灵活应用该方法解决实际学习生活中遇到的问题，从根本上提高自身数学解题能力，获得更加准确地结果.