“模型建构法”对提升中学生物理解题能力的作用

◇ 甘肃 丁国栋

高中物理难学，体现为学生在学习中存在诸多问题，面对综合性强的题目容易思维混乱，不能做到灵活变通.另外，大部分学生基础薄弱，很多教师上课过程中为了夯实学生的基础知识会将不易理解的知识和题目删减，导致学生对物理问题认识不够深刻.如此一来在高三的一轮复习中便会举步维艰，学生学习时没有条理，教师教学不得章法，物理教学陷入一种尴尬、被动的局面.高考不会因为一部分学生基础差而降低难度.各学校在分析高考试题时，常将试题难度比例划分为7∶2∶1.事实上，不去锻炼尝试一些难题、综合题，不能从中总结解题方法和经验，高考中70%的简单题目对基础薄弱的学生来说也是难题.我们要想办法，找到教学和学习的出路.

物理是一门“来源于生活而又应用于生活”的学科，物理学解决的就是生活实际问题，而生活实践又在时时刻刻论证着物理学科知识.许多生活现象、热点问题(诸如卫星发射、水流星、汽车刹车制动等)都可以在物理中找到相对应的模型.所谓“模型建构法”就是把研究对象(原型)一些次要的细节、非本质的联系舍去，以简化或者理想化的形式去再现原型的各种复杂结构、功能和联系的一种科学方法.在中学阶段物理学习中，学习成绩的评定是一个重要的环节.很多题目设计的背景都来源于生活实际.在一些综合性的题目中，更是涉及对生活现象多方面的考查.“模型建构法”能够帮助学生将复杂、抽象的物理过程简化为若干学生容易理解的模型结构，有助于学生找到各个模型之间的连接点或相同的物理量等，进而各个击破，准确解题.

在具体教学中，学生面对综合性强的问题束手无策，无法从繁杂的过程中找到有用信息.此时，教师就需要努力帮助学生建构模型，将抽象、难以理解的知识简化，把题目转化成学生更容易接受的形式，使解题水到渠成.“模型建构法”在牛顿运动定律、圆周运动、(类)平抛运动、电磁感应等专题知识中都有广泛应用，下面笔者以动能定理为例，谈一谈教学中的几点感悟.

1 动能定理分析应用

高中阶段运用动能定理解题是教学中的难点，它融合了动力学、电磁学以及数学等方面的知识.在高考中，学生面对多过程、多物体的问题时，如果全局意识不强，对题目整体把握不好的话，稍有不慎就容易全盘出错.在这一专题的教学中，笔者一开始就实行“模型建构法”教学，即帮助学生把生活中常见的运动情况通过受力分析、力的分解等知识简化为一张草图.学生通过图形对比，很容易掌握其中的规律，甚至可以达到熟练记忆、无图自圆其说、准确解题的程度.

1.1 常见运动情况模型建构

常见运动模型如图1所示.

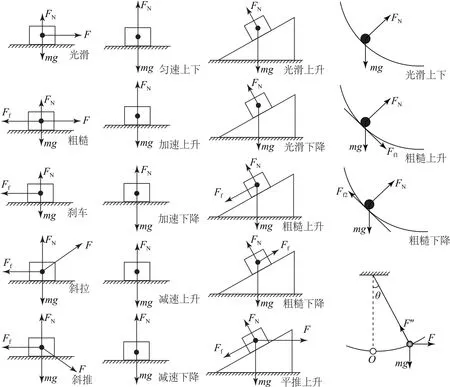
图1

1.2 动能定理解题步骤

1)明确研究对象；

2)判断物体运动模型图；

3)分析物体运动情况，明确初、末两个状态；

4)应用动能定理解题.

1.3 对动能定理的几点认识

1)对于直线运动，无论是物体在水平、竖直，还是斜面上的运动类型，都可以用力学、运动学的知识，也可以用动能定理解题；对于曲线运动、变力做功等问题，解题只能用动能定理.

2)如果题目中出现光滑(不计阻力)字眼，首先考虑能否应用机械能守恒定律求解瞬时速度或是高度等；如果题目中出现粗糙(摩擦、空气阻力)字眼，则必须用动能定理解题.

3)机械能守恒定律如同匀速直线运动一般，属于特例；机械能不守恒如同变速运动一般，才是生活中的普遍现象.因此在解题过程中，动能定理的应用才是纵观全局的大方向.

4)动能定理表达式W 总＝Ek2－Ek1中左边为功，右边为能.动能是一个状态量，对应某个点，只要我们知道某一点的瞬时速度，很容易确定动能.动能定理应用真正的重难点还在于功，即各个力对物体所做的总功.因此学生能否对一个物体进行正确的受力分析尤为重要.

5)极限分割法.一段曲线三等分或六等分后每一小段还是曲线，而无限分割下去，每一小段趋于直线，此刻物体所受支持力或是拉力方向与直线成垂直关系，则支持力(拉力)对物体不做功.

2 典例剖析

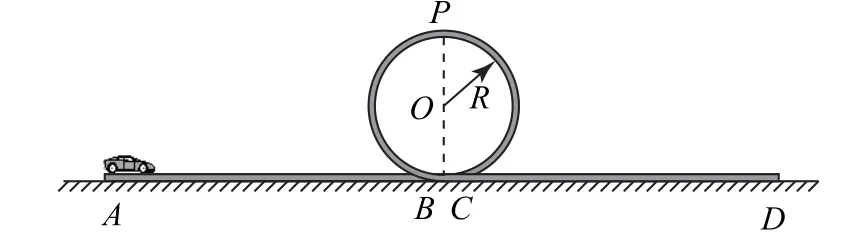
图2

(1)小车在CD 轨道上运动的最短路程；

(2)赛车电动机工作的时间.

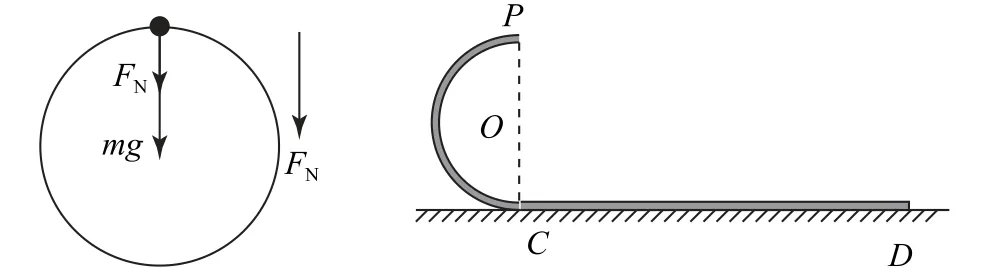
图3

分析(1)本题先构建“圆周运动”模型，先找最高点向心力方向：竖直向下.后进行受力分析：重力mg 与支持力FN，再列式计算：Fn＝mg＋FN(分析题目可知对应P 点处取最小速度，则为临界状态，求得P 点最小速度).

本题为曲线(光滑下降)＋刹车模型的综合.遵照动能定理解题步骤，列方程有W 总＝Ek2－Ek1，即代入数据得出答案.

(2)整体运动过程为粗糙＋曲线(光滑上下)＋刹车模型的综合.按照动能定理解题步骤，列方程有

想要正确求解本题，需要学生准确判断各段受力情况和做功情况，并知道圆周运动中，赛车向上、向下过程中重力分别做正功、负功，总功为0.

高考对于动能定理的考查，层次要求高，甚至会融合电磁场、传送带等专题内容.事实上，各个模块的专题知识都可以建构各自的模型，最终将一道综合题分解为多个模型，学生找到模型之间的衔接点，各个击破，即可准确解题.学生虽然基础薄弱，但拥有一定的知识积累，所以教师在教学中要引导学生从繁杂走向简单，从简单中认清题目的本质，进而拓展延伸，理解生活现象所蕴含的道理.“模型建构法”不可能将每一个专题涉及的模型一一列举，在引导学生熟练掌握几种典型模型后，就需要知识升华进一步理解公式或者规律的本质，进而在变化多样的题目中灵活应用，使学生能够用自己掌握的方法进行分析处理，最终体会到“多元合一”的本真思想.