海洋平台复杂结构焊接残余应力高效预测及焊接顺序优化

施一丰，邹家生，赵宏权，刘 川

(江苏科技大学 江苏省先进焊接技术重点实验室， 镇江 212003)

海洋钻井平台为大厚度复杂焊接结构,其工作环境恶劣,对焊接质量的要求苛刻．轴承座作为海洋平台重要的工作部件,所用的材料强度高,焊缝分布集中,加上结构本身拘束度大,极易产生高幅值且分布复杂的焊接残余应力．焊接残余应力会影响焊接构件稳定性,降低焊件的使用寿命,造成焊接结构破坏[1]．因此,对海洋平台轴承座之类复杂结构的焊接残余应力的分布、形成机理、影响因素等进行分析和预测,并提出减小应力的措施,是该类焊接结构设计生产的前提和保障结构服役安全的基础[2]．

影响焊接应力变形的因素众多,如拘束、材料、坡口形式、焊接工艺和方法、焊接顺序等[3]．其中焊接顺序是影响海洋平台轴承座之类多构件、多焊缝交错大型复杂结构应力及变形的重要因素．通过反复试验获得焊接顺序的方法费力耗时,且很可能因为不能全面分析各焊缝的相互影响而无法获得最合适的焊接顺序．热弹塑性有限元焊接应力变形数值计算方法具有高效、经济、结果全面且能分析焊接应力演化历史等优点,已经成功应用于焊接应力变形机理、调控、分布状态预测和焊接顺序优化等方面[4-5]．但有限元数值模型和假设条件的合理性,计算方法的可靠性以及计算结果的有效性仍需要一定的试验验证．因此,少量试验和大量数值计算是当前研究焊接问题的主要方法．此外,热弹塑性有限元法焊接应力变形数值计算是一个高度非线性的热-力耦合过程,计算效率低下．提高焊接应力变形数值计算效率是国内外学者和工程技术人员关注的热点,最近几十年提出了诸多高效算法和思路[5]．将多种高效方法综合应用,在常规计算机工作站上实现大型复杂结构高效计算,分析预测大型复杂结构的应力分布状态、演化过程、服役寿命和优化工艺等是焊接应力变形数值计算的一个发展方向．

针对海洋钻井平台用轴承座复杂焊接结构,综合多种高效方法,实现多构件、多焊缝交错结构的焊接应力变形高效数值计算,结合试验验证计算结果;并进行焊接顺序的优化计算,分析多构件焊接应力集中区域形成的原因．

1 轴承座结构及计算模型

图1为钻井平台上的轴承座结构,该结构由251 mm厚的轴承座(A514Q),38 mm厚的肘板,38 mm厚的月牙板(EQ47),32 mm厚的前板(EH36)组成．月牙板和其他构件连接的坡口形式为单V形,共焊接35道;其余焊缝坡口均为K形,焊道数量为19～25道;整个轴承座的总焊接长度为380 m．

图1 轴承座焊接结构(单位：mm)Fig.1 Welded structure of bearing pedestal(unit:mm)

该结构的焊缝和焊道数多,焊接总长度长,结构复杂,材料种类多,并包含两种坡口形式,对其进行焊接应力变形有限元分析非常耗时．为提高计算效率,综合多种高效计算方法实现该结构焊接应力变形数值计算,主要有:

(1) 考虑到结构的对称性,取其一半模型分析,如图2(a)．根据图2(a)的模型特点和焊缝之间的相互影响,将计算模型再次拆分成A、B两个部分进行模拟[6],拆分后B部分模型如图2(b),图中焊缝的编号即焊接顺序．

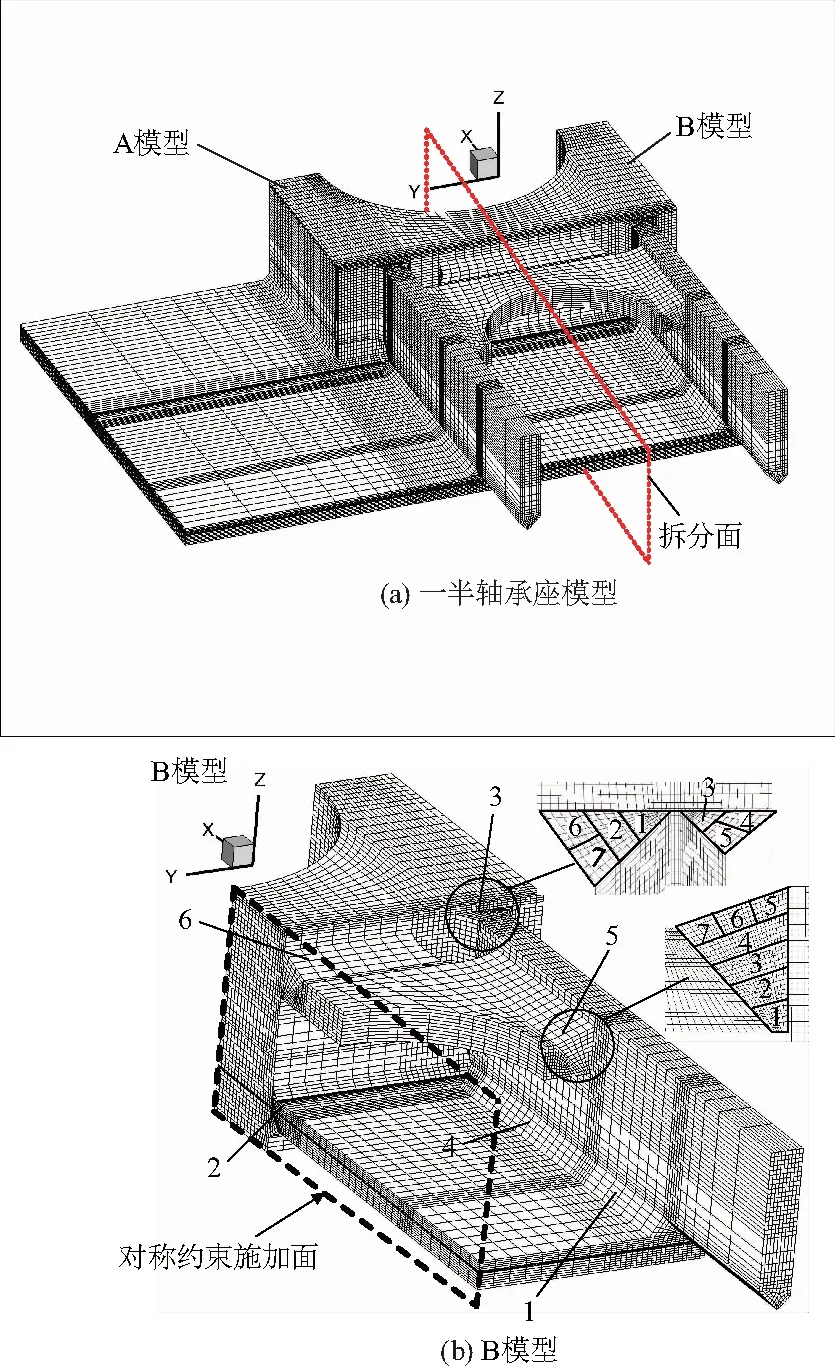
图2 轴承座结构计算模型Fig.2 FEM of bearing pedestal

(2) 采用带状温度热源[7]提高温度场计算效率．利用ANSYS软件生死单元技术模拟焊接填充过程,首先将所有焊缝单元杀死,焊接开始时激活当前焊道的一段单元并施加熔化温度载荷作用一段时间,然后删除当前温度载荷,并激活下一段单元施加温度,以此实现焊接热源的移动．该分段温度热源的参数少(仅为温度作用时间),温度场调试方便．热源作用时间可根据公式(1)估算．轴承座的焊接工艺参数如表1,焊前预热150 ℃．轴承座的热源作用时间在2.6～3.2 s．

(1)

式中:t为热源作用时间，s;p为由采用的焊接方法而定的常数，mm·kW-1,对于熔化极气体保护焊,p取3.8～4.8;U为焊接电压，V;I为焊接电流，A；v为焊接速度，mm·s-1.

表1 轴承座焊接工艺参数Table 1 Welding parameter of the bearing pedestal

(3) 焊道合并简化方法[8],即将多道焊道合并为一道,使计算焊道数显著减少从而缩短计算时间．但焊道过分简化会造成计算精度降低．针对轴承座结构的K形和V形坡口形式,基于二维模型进行大量的计算,并考虑到表层焊道对应力的贡献显著,最终获得最优的焊道简化方式,内部焊道两层合并为一层,盖面焊道应该少量合并为两道以上,即V形坡口由29道简化为7道,K形坡口由16道和23道简化为7道,见图2(b)．

(4) 力学软化温度和预条件共轭梯度算法(PCG)．应力场计算时,不考虑分段热源每段作用时的升温阶段,仅考虑每段热源降温阶段对应力变形的贡献,且每段激活单元施加的温度载荷为材料的力学软化温度(采用1 200 ℃)．软化温度方法能提高计算收敛性,从而提高效率,且对计算结果影响小．此外,采用PCG算法和多核并行算法进一步提高效率．

图2中A模型和B模型计算过程相似,因此，仅以B模型为例介绍轴承座应力计算结果和焊接顺序优化结果．B模型有6条焊缝,每条焊缝简化为7道,共42道焊缝,有限元模型包含79 720个单元和88 830个节点,焊缝区域的单元尺寸小于3 mm．

整个计算过程为热-力耦合顺序计算,即先进行瞬态温度场计算,然后将温度场结果作为力学计算的载荷获得应力场分布．温度场计算时,与空气接触区域施加自由对流边界条件．应力场计算时,模型的拆分面施加对称边界条件,并在前板远离焊接区域的节点施加额外的位移边界条件,避免结构的刚性移动．设所有构件的材料为双线性随动强化模型,且服从米塞斯屈服准则;各构件随温度变化的材料热学和力学性能见图3．

图3 材料属性Fig.3 Thermal and mechanical properties

2 计算结果

2.1 结果验证

图2(b)为B模型在Dell precision T5600工作站上总计算时间约为100 h．为了验证计算结果,焊接了图1的模拟件,并采用小孔法和X射线衍射法(XRD)测试模拟件局部区域的残余应力,测试区域和现场测试见图4,L1、L2和L3线分别位于图2(b)中的焊缝3、5和6．将计算结果与测试结果比较,见图5．图5(b)和图5(c)所示沿L2、L3计算和测试的y向应力差距较大．这是因为L2和L3线位于窄小的焊缝区域上,测试比较困难,造成测试误差较大所致,此外,计算所采用的一系列简化和假设也会带来一定误差．总体而言,图5中3条评价线上的计算与试验测试应力分布趋势基本吻合．说明采用的计算模型和高效计算方法能在常规计算机工作站上实现复杂焊接结构的应力数值计算,计算结果可以全面反映结构的应力分布特点,模拟方法兼顾了效率和精度．

图5 试验和数值计算结果比较Fig.5 Comparison between simulated resultsand experimental ones

2.2 残余应力分布

图6为B模型计算的变形和残余应力分布．图中看出肘板产生较大向内侧的y向位移(图6(a))．图6中焊缝3(肘板与轴承座)的三向应力均为拉应力,其中两侧焊趾位置出现超过700 MPa的拉应力,肘板的最大变形达4.5 mm．该轴承座结构在服役过程中,焊缝3的三向拉应力和外载荷叠加,极易在该焊缝区产生裂纹,影响整个平台的服役安全性．焊接残余应力主要是焊缝冷却过程的横向和纵向收缩受到周围材料的拘束产生的．分析认为焊缝3纵向拉应力(z向应力)是因为焊缝3本身的纵向(z向)收缩引起的,x方向拉应力较大(720 MPa)是因为焊缝6的纵向收缩(y向收缩)造成对肘板的附加弯矩,引起肘板y向变形(图6(a)),从而使焊缝3外侧焊缝受拉所致．焊缝4、焊缝5和焊缝6的焊接顺序是造成焊缝3上x,y方向应力大的原因．因此有必要对该结构的焊接顺序进行优化．

图6 B模型残余应力和变形计算结果Fig.6 Displacement and stress distributions of part B

3 焊接顺序优化计算

基于建立的有限元模型,设计5种焊接顺序(图7),计算各焊接顺序下的应力分布．选取轴承座和肘板焊缝的外侧线L1(图4),比较沿该线上各焊接顺序计算的残余应力．

图7 焊接顺序示意图Fig.7 Schematic diagram of the welding sequences

图8是各焊接顺序计算的沿L1线应力分布结果．从图8看出,焊接顺序4计算得到的沿L1线上焊缝区域的x方向、y方向和z方向应力明显比其他焊接顺序计算的应力值低,且焊缝区域的x方向和y方向应力降低更显著．焊接顺序1计算的L1线上x方向明显高于其他焊接顺序,其原因是:当焊接焊缝6时,肘板已经和前板、轴承座焊接在一起,肘板的厚度和宽度相对与轴承座和前板而言较小,其刚度较小,焊缝6的纵向收缩力(y向收缩)通过月牙板向肘板施加了向内的弯矩作用,造成肘板向内侧变形,焊缝3被施加了附加应力,从而造成其焊趾位置应力集中．当采用焊接顺序4时,月牙板先和轴承座的焊接在一起(图7(d)焊缝4),其纵向收缩力不能作用在肘板上,因而不会造成对焊缝3的附加弯矩;最后焊接月牙板和肘板(图7(d)焊缝5),尽管该焊缝的收缩也会施加作用力于肘板上,但焊缝5的纵向收缩力为x方向,肘板在该方向上刚度大不易变形(板内变形),且和焊缝1的纵向收缩力作用效果相反,因而几乎不会产生对肘板的附加弯矩,从而避免了焊缝3的x方向应力集中;其余焊接顺序都无法避免造成对肘板的附加弯矩,因而引起焊缝3(图7(a)焊缝3)肘板侧焊趾的x方向应力集中．

图8 沿L1线的应力分布Fig.8 Stress distributions along L1

焊接顺序1造成焊缝3的y方向应力集中是因为焊接顺序1中,肘板的y向刚度小,易发生y向变形(板外变形),焊缝5的纵向收缩(x方向)给肘板施加弯曲作用力,易造成肘板y向外侧弯矩,因此使得焊缝3轴承座侧的焊趾位置产生y向应力集中．从以上分析可知,多个构件焊接时,刚度较小的构件(或构件刚度小的方向)易受到其他构件焊缝的影响产生变形,从而产生附加弯矩,增加焊趾处的应力集中．因此,焊接时应避免产生刚度较小构件受到易变形方向的弯矩作用,从而避免产生附加弯矩造成的应力集中．此外,避免构件在强拘束状态下焊接,也是避免焊缝应力集中的方式．焊接顺序4中将1和4合并,降低了顺序1中焊缝4焊接时肘板所受的拘束度,一定程度上降低了焊缝3的应力集中．

图9为焊接顺序4计算的应力和变形分布云图．比较图6和图9,焊接顺序4造成的肘板y向变形明显小于焊接顺序1,最大变形降为2.25 mm,同时由图8(a)看出焊接顺序4中焊缝3的x方向应力明显小于焊接顺序1的结果．综上分析,焊接顺序4避免了刚度小的肘板(易发生y向板外变形)承受后续焊缝收缩造成的弯矩所引起的附加应力,因此获得的肘板-轴承座焊缝(焊缝3)x应力峰值结果降为320 MPa以下,y向和z向残余应力分别比焊接顺序1均有明显地下降．

图9 B模型焊接顺序4计算结果Fig.9 Displacement and residual stress distributionof the fourth welding sequences

4 结论

(1) 基于焊道合并简化技术,并综合带状移动温度热源、软化温度法等方法能够在常规工作站上100 h内实现海洋平台用轴承座之类大型复杂多焊缝焊接结构应力变形的高效预测,应力的计算结果由试验检测验证,结果合理;在此基础上进一步分析应力集中区域产生的原因,完成大型构件的焊接顺序优化计算．

(2) 多个部件组成的复杂结构焊接时,刚度小的部件受到后续焊缝的影响较大,易产生变形,从而对其他刚度大的焊缝产生附加弯矩引起部件焊缝的应力集中．通过焊接顺序优化计算,可以避免其他部件焊缝因刚度小的部件变形过大而受到额外较大的弯矩,从而降低焊缝的三向拉应力．