一种多功能单跨梁振动实验系统

2 张 梁

(1.天津大学 建筑工程学院，天津 300072；2.滨海土木工程结构与安全教育部重点实验室，天津 300072)

0 引言

在土木学科课程和土木领域研究中，梁的振动问题以及梁振动固有频率的研究具有重要的理论和应用价值，但是由于梁振动问题过于复杂，实验难以操作，因而在梁振动实际教学和研究中很难将理论和实践结合起来[1]。实际上，为了实现梁振动问题的实践教学与研究，部分高校和科研机构相继开发了一系列振动教学系统。张蔚波等[2]基于市场上已有的振动教学系统研制了简支梁形式的振动教学平台；李建康等[3]研制的三自由度弦振动的模态教学装置在各类振动实验教学平台中被广泛采用；李兆军等[4]研制了能对离散质量、梁和轴振动的振动实验台；任张晨等[5]采用传统锤击方法测得了四不等跨连续梁的固有频率，并将有限元软件分析计算结果与实验得到的结果进行分析比对，验证了实验的可靠性；刘爱民等[6]用将悬臂梁固定在支架上剪断自由端悬挂重物的方式对悬臂梁结构进行了动力学分析；曹东兴[7]通过搭建实验平台研究了简谐荷载作用下方形截面悬臂梁的非线性振动特性。上述几种梁振动教学平台和研究装置，或限于弦振动，将质量集中在几点与实际梁模型相差甚远；或形式较复杂，操作较为麻烦；或激励方法较为传统，实验数据不能保持较好的稳定性和连续性，因而不能很好地用于梁振动的教学和研究。为了更好地开展梁振动问题的教学与研究，开发了一种结构简单、布置灵活的多功能单跨梁振动实验系统，利用该振动实验系统开展了实验，并将实验结果与数值解进行比对，结果吻合较好。该振动实验系统具有较好的精度，可以用在土木学科梁振动教学实践和基础理论研究中,也可用于复杂的随机振动实验。

1 多功能单跨梁振动实验系统构建

1.1 多功能单跨梁振动实验系统

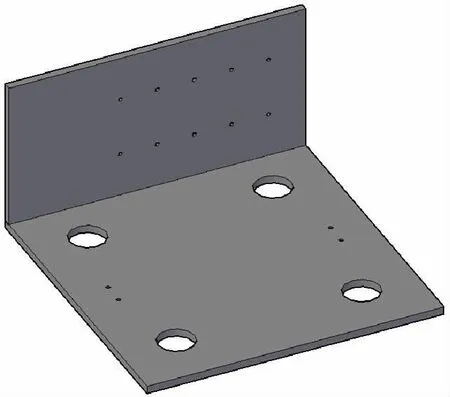
图1 系统底座

多功能单跨梁振动实验系统的设计要满足3个要求：①能实现多种形式梁振动实验；②能够实现不同激励荷载和激励点的施加以丰富实验内容；③能够通过数据直观地观察梁振动曲线，并应具有较高的精度。整个梁实验系统由底座、支座、激振器、位移传感器、力传感器和数据采集处理系统6部分组成。底座由板1和板2通过角焊缝连接，焊缝要通过计算校核保证不会出现破坏、局部失稳或整体失稳[8]。板1尺寸为800 mm×400 mm×10 mm，并且根据激励点加载位置不同在板面上预留相应螺栓孔用来固定激振器；板2尺寸为800mm×800 mm×10 mm，根据梁支座位置预留相应螺栓孔以固定支座。底座拼接效果如图1所示。支座设计成2种形式，分别为简支端支座和固定端支座，为了减少约束对梁振动实验的影响，支座应具有较大的刚度，支座尺寸和三维图如图2所示。激振器使用强力电动式模态激振器，其可以为梁提供最大激振力为100 N、最大振幅为10 mm的激励；力传感器采用动态力传感器，其一端通过顶针与激振器连接，另一端与试件梁连接，为保证梁仅在激振器激励作用下振动而不是与激振器协同振动，力传感器与试件梁之间不能采取固定约束，在实验时通过调节顶针使力传感器与试件梁轻微预压紧即可；位移传感器采用激光位移传感器，其测量范围在±60 mm，分辨率8 μm，具有较高的精度。实验系统工作原理示意图如图3所示，实体图如图4所示。

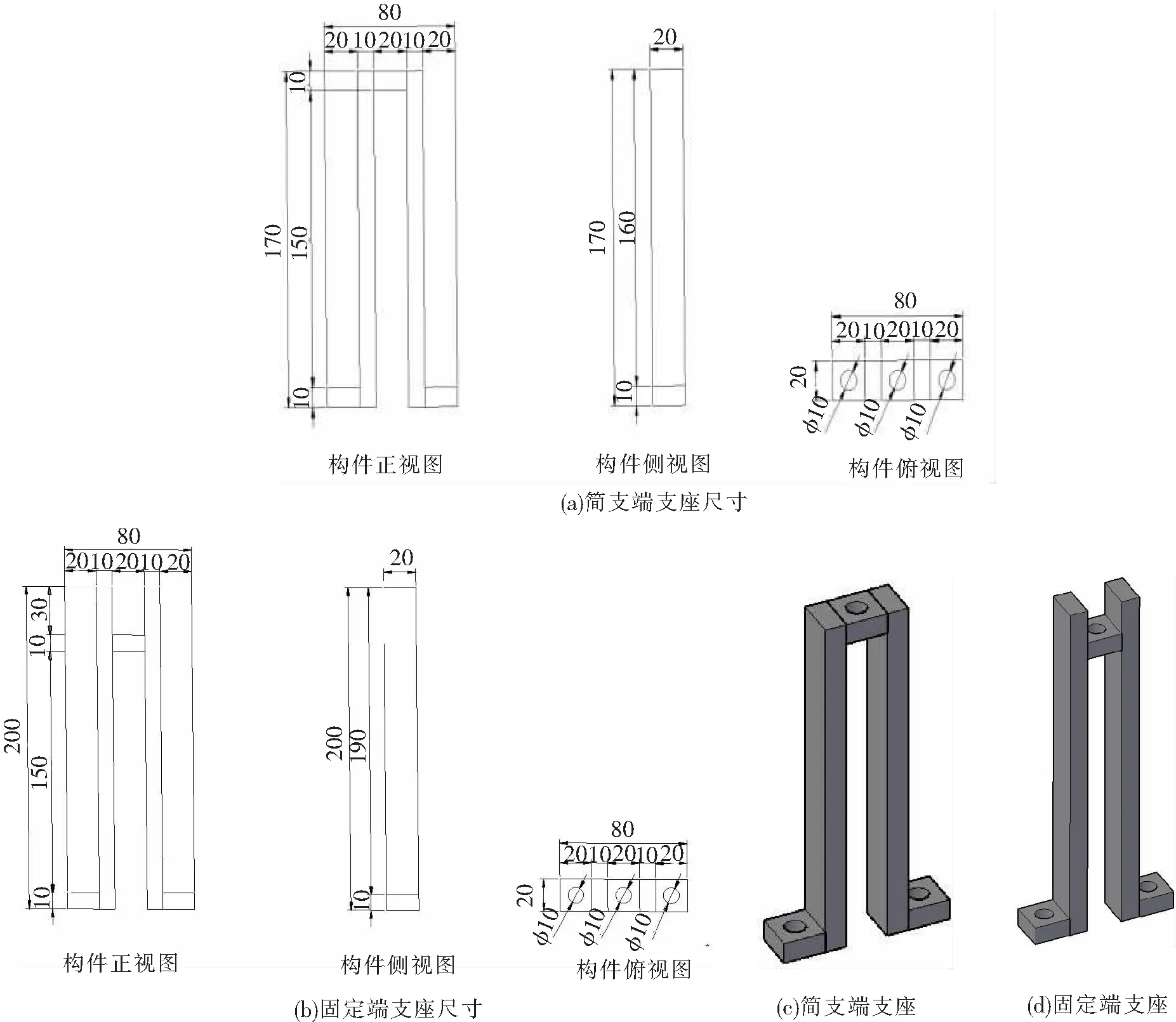
图2 支座尺寸和三维实体图(单位：mm)

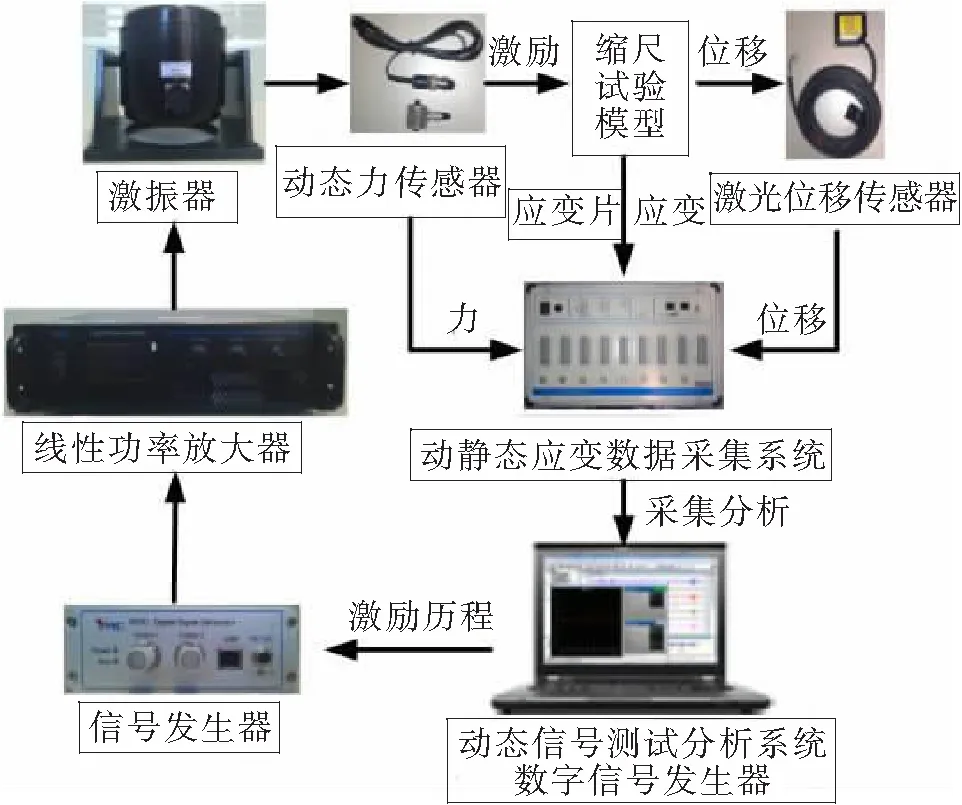
图3 实验系统工作原理示意图

图4 系统组装实体图

1.2 梁振动工况方案

为验证上述单跨梁振动实验系统的可靠性，制作了3根截面尺寸不同的钢梁进行实验，钢梁长度均为620 mm，其截面尺寸如图5所示。根据底座上预留螺栓孔，可以将激振器固定在不同的位置，实现不同激励点加载，结合支座的固定形式，可以有以下振动工况组合方案，共计36种，其排列组合如表1所示。

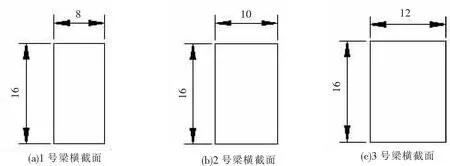
图5 试件梁截面图(单位：mm)

表1 振动工况组合方案值

2 梁振动实验测试结果

2.1 强迫振动

使用上述研发的单跨梁振动实验系统，选取几种典型工况进行了振动实验。实验中选用正弦波作为激励荷载，为了能够较好地采集钢梁的振动数据，实验中调节信号源正弦波信号的频率为10 Hz,振幅通过线性功率放大器的输出电压控制，分别为0.6 V、1 V、1.4 V。实验工况如表2所示。

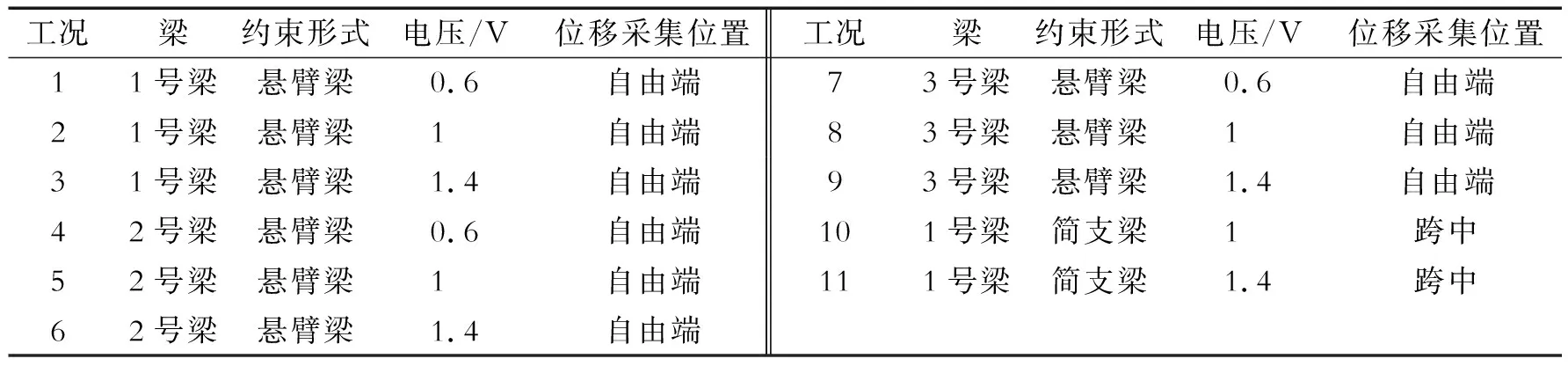
表2 实验工况

对于表2中所列出的工况进行振动实验，悬臂梁的加载点和振动位移监测点分别选取跨中1/2处和自由端点处，简支梁的加载点和振动位移监测点均选取跨中1/2处，部分工况的振动位移时程曲线和激振力时程曲线如图6和图7所示。

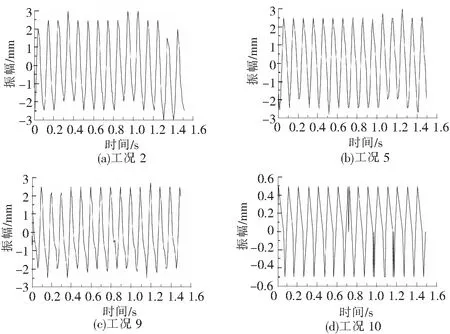
图6 振动位移时程曲线

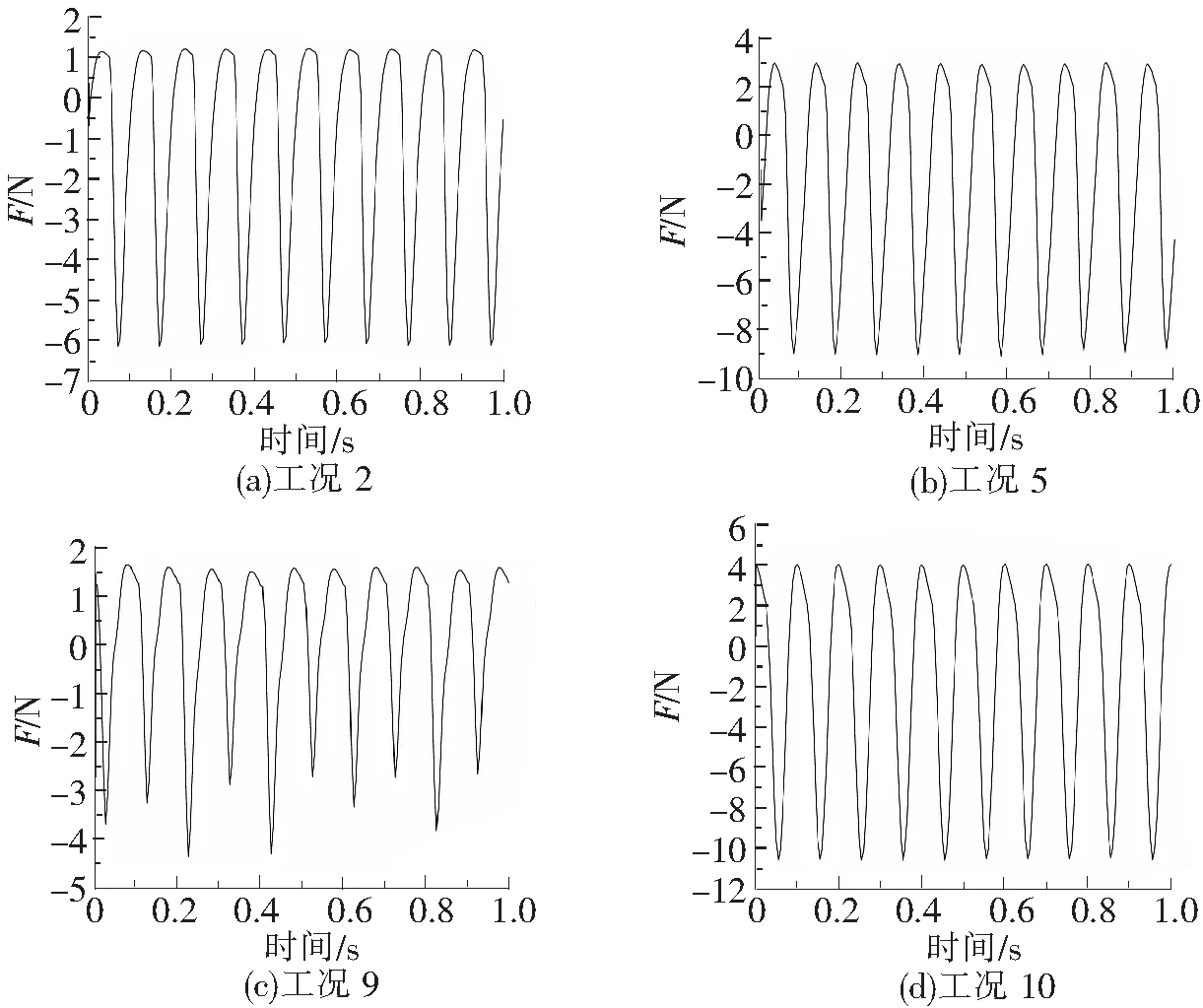
图7 激振力时程曲线

2.2 模态分析

使用上述研发的单跨梁振动实验系统，分别对工况1、工况4、工况7钢梁试件进行扫频，扫频波形选用正弦波，扫频范围为5～100 Hz，扫频时间选为20 s，扫频时间不易过小同时也不易过大，如果时间过小则每个频率停留时间过于短暂，位移传感器不能够有效采集到相应位移；如果时间过大，则在每频上采集数据点过多，位移时程曲线失真，影响模态分析结果。在扫频过程中，梁的振动是一个非常复杂的随机振动过程，其振动频率在0到无穷大之间连续变更，可以用非周期性函数来描述这种振动的过程。非周期波形不能直接展开成为傅里叶函数，但在研究时可以将其看成一个周期无穷大的周期波，其频谱是连续频谱[9]。模态分析主要考虑加载方向平面外振动，对3根钢梁扫频得到位移时程曲线经过快速傅里叶函数转化(FFT)便可得到相应的频谱，3根钢梁在以上3种工况下的频谱如图8所示。

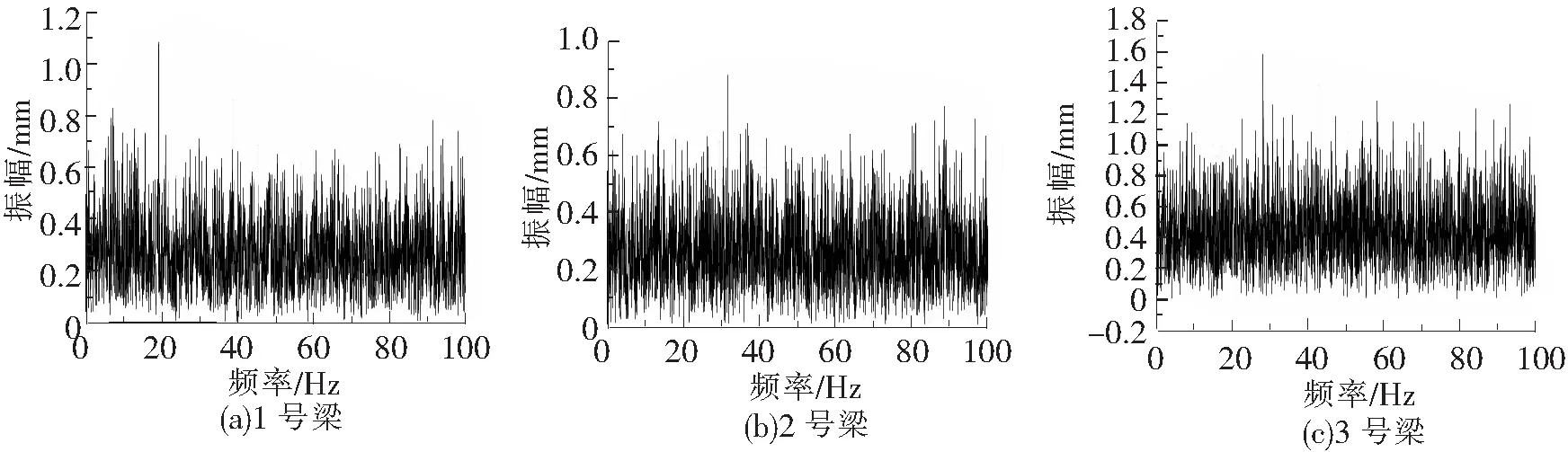
图8 频谱分析图

3 数值模拟与结果对比

3.1 数值模拟

采用ABAQUS建立梁的三维实体单元模型，为了简化模型，模型中不对激振器加载顶针建模，而只是在顶针一端的受力点处定义一个参考点，然后在此点和梁表面之间建立分布耦合约束，从而模拟激振器顶针与梁的连接关系[10]。梁材料为Q235，密度为7 850 kg/m3，弹性模量为210 GPa，泊松比为0.3。将实验中采集得到的激振力作为加载荷载幅值，得到数值位移时程曲线，如图9所示。

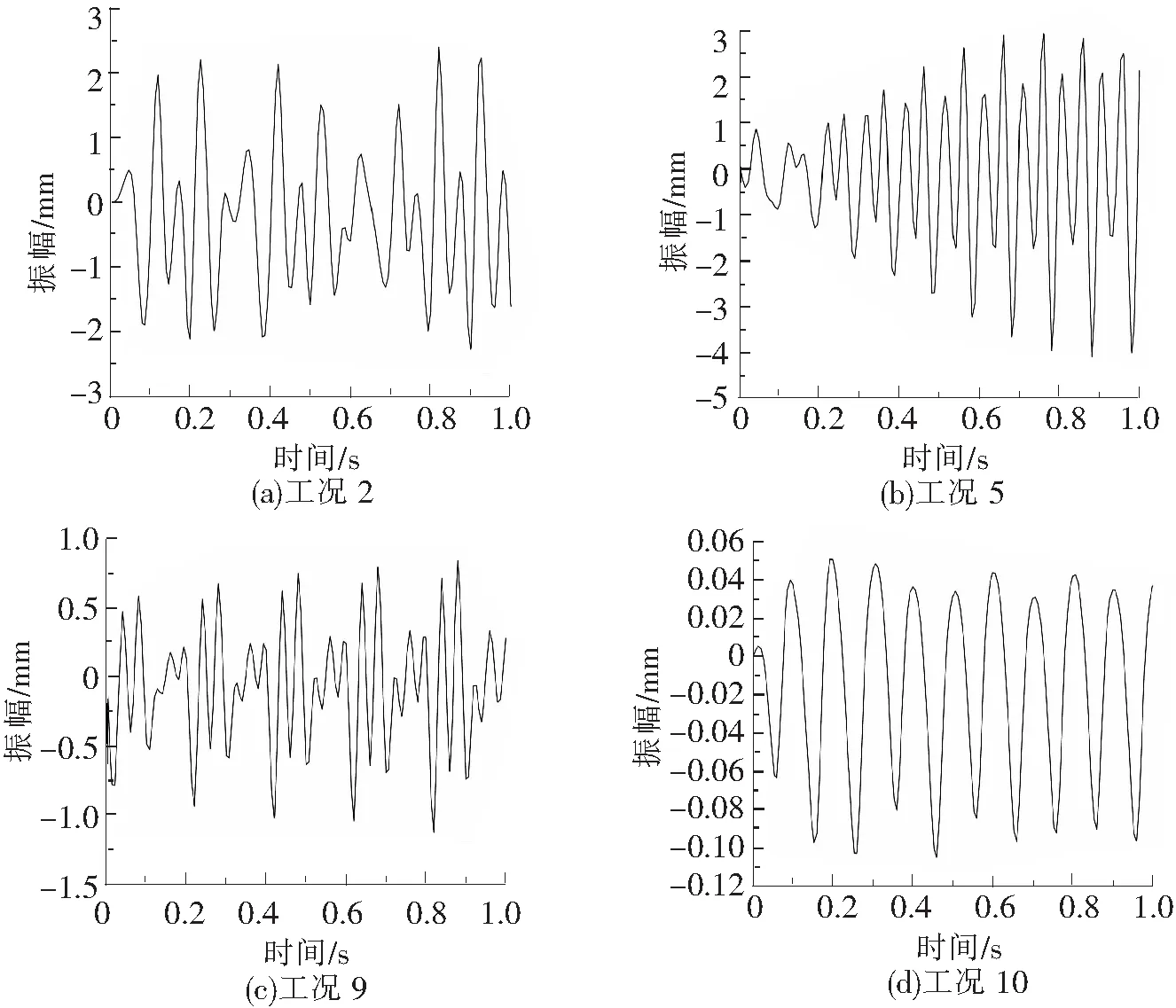
图9 数值位移时程曲线

3.2 结果对比

将实验中采集到的位移时程曲线平均振幅与数值模拟位移时程曲线平均振幅进行比对，结果如表3所示；实验模态分析结果与数值模态分析结果比对如表4所示。

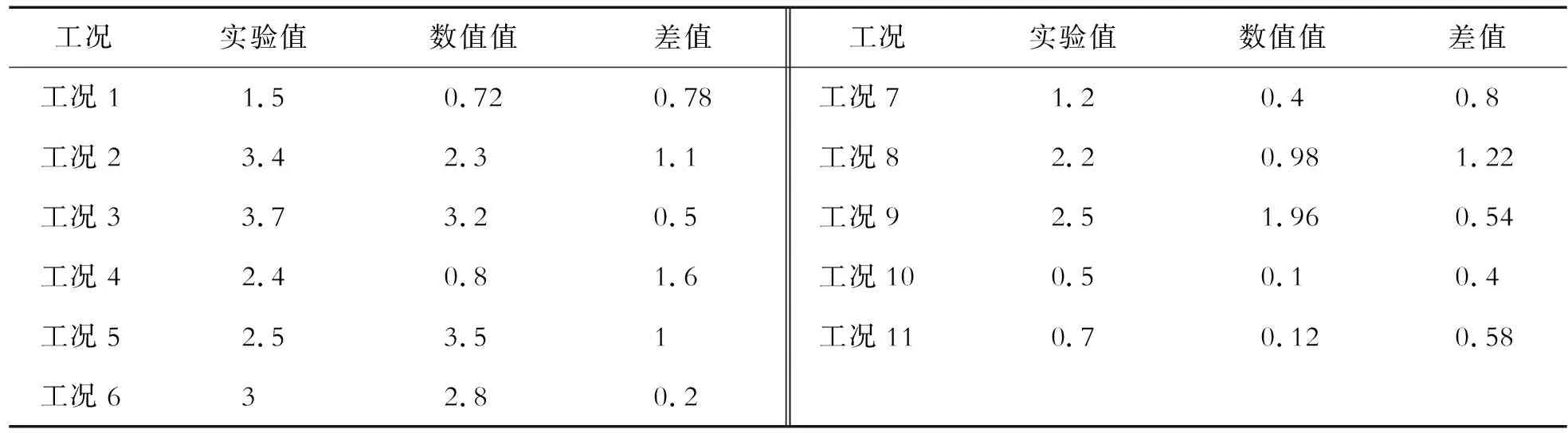
表3 振幅结果对比 mm

表4 模态分析结果对比 Hz

3.3 误差分析

从实验结果和数值模拟结果对比来看，该振动实验系统具有较高的精度。振幅误差最低为0.2 mm、最大为1.6 mm，相对误差可达到7%左右；模态分析误差最大为4.8 Hz,最小为2.2 Hz，相对误差可达到10%左右。误差的主要原因有：①振动实验系统中采用的位移传感器和力传感器都为高精密元器件，在实验中,振动平台自身产生的微小振动会对实验结果造成很大的误差；②振动实验系统中梁支座刚度有限，而在数值建模中为了简化模型将支座刚度简化为无穷大，从而造成一定的误差；③振动过程中，激振器顶针与梁不能一直保持较好理想接触，部分时间存在脱离，在数值模拟中顶针与梁接触理想，致使实验结果与数值模拟结果存在误差；④实验中振动位移采集点与数值模拟中位移监控点不完全是同一点，造成实验结果与数值模拟结果误差。

4 结论

(1)开发了一种多功能单跨梁振动实验系统，该振动实验系统结构简单，操作方便，能实现多种形式梁振动实验，可用于梁振动、模态分析等课程的实践教学，丰富土木类本科生和研究生的教学实践，为进一步加强和提高学生在梁振动方面的实践和创新能力提供平台，也为梁振动基础理论研究和随机振动研究提供一种实验手段。

(2)设计了3根不同截面的梁，进行了11种不同工况的振动实验，并对3根悬臂梁进行模态分析。将实验结果与数值模拟结果进行比对，结果吻合较好，表明该单跨梁振动实验系统具有较高的精度。

(3)深层次分析了该单跨梁振动系统在实验中产生误差的原因，为今后利用该系统进行梁振动实践教学和基础理论研究进行误差分析提供参考。