砌石挡土墙稳定性的模型试验及数值模拟

毕继红，2, 袁琳琳, 赵 云, 霍琳颖

(1.天津大学 建筑工程学院，天津 300050；2.滨海土木工程结构与安全教育部重点实验室，天津 300072)

挡土墙作为支承路基填土、防止填土或土体变形失稳的构造物，结构简单、施工方便、占地面积少且造价低廉，广泛应用于公路、土木、水利等行业的相关工程。近年来由于大规模的自然灾害，挡土墙的崩塌令人担忧，其稳定性研究具有重要的工程应用价值。

目前，就挡土墙的稳定性分析问题，国内外学者已经做了一些工作。张晓曦等[1]运用极限分析原理，研究了地震作用下挡土墙的滑裂面倾角及稳定性问题。贾亮等[2]在水平条分法的基础上，推导出了挡土墙内部稳定性的分析方法。文献[3-6]进一步研究了边坡稳定性涉及到的随机变量如内摩擦角、断层倾角、填土重度等。然而，挡土墙的稳定性受到岩体结构、力学作用等因素的影响，具有非线性、不确定性、可变性等特点，通过以上计算方法研究挡土墙边坡稳定性的过程较为繁琐且结果单一。另外，有部分学者通过室内试验和现场实测对挡土墙边坡稳定性进行了研究。杨山奇等[7]采用模型试验的方法，研究了平移模式下挡土墙后破坏滑裂面的空间形态。Villemus et al[8]通过室内试验和现场实验，研究干石挡土墙的稳定性及破坏模式。但是试验耗时耗力，并且无法精准地反映加载过程中挡土墙各部分之间的相互作用及土体的塑性发展，而利用数值模拟能够准确地捕捉挡土墙的应力变化，多方面定量分析挡土墙的稳定性，有助于更好地理解挡土墙的破坏过程。冯复兴[9]借助有限元软件研究了墙面板刚度对加筋挡土墙抗震性能的影响。甘发达等[10]使用有限元软件RW2DPS建立重力式挡土墙模型，分析了挡土墙在强震作用下的反应。Li et al[11]通过大量的有限元分析研究了变速率荷载作用下挡土墙后土压力的分布规律。Chen et al[12]建立二维有限元模型，分析了加筋土挡土墙加固措施对其稳定性的影响。文献[13-15]以实际工程中的挡土墙结构为研究背景，通过数值模拟分析了挡土墙的变形特性、滑移模式以及受力特点。

然而，挡土墙各部分之间的相互作用在上述研究中未被充分考虑。以某山区公路挡土墙结构为研究背景，在倾斜试验的基础上，建立二维、三维有限元模型，并在砌石挡土墙的多个关键位置设置接触，研究挡土墙在倾斜荷载作用下的稳定性，分析倾斜过程中挡土墙的变形、砌石间接触压的分布及背后填土塑性区的变化，探究挡土墙的破坏机制，以期为挡土墙的抗震和加固分析提供参考。

1 试验简介

图1 试验装置

1.1 倾斜试验

倾斜试验可以在拟静力分析中对模型施加静态水平体力，利用金属丝吊起背面地基，使挡土墙前方的作用力增加。如图1所示，试验模型建立在长1 850 mm、宽600 mm、高850 mm的加载装置内，其中，加载装置一侧为透明有机玻璃，便于观察挡土墙和墙后填土的变形。倾斜速度约为1°/min，直至模型完全崩塌。水平地震系数kh计算公式为

kh=tanθ

(1)

式中,θ为倾斜角。

1.2 试验模型

作为模拟方法的验证试验，对实际大规模公路砌石挡土墙的抗震性能进行了试验。挡土墙高度为720 mm，厚度为600 mm。挡土墙所用砌石采用干砌的砌筑方法，尺寸为66 mm(长)×45 mm(厚)×99 mm(高)，由无收缩性水泥砂浆制作而成。该模型试验中，加载装置内部几何尺寸为1 850 mm(长)×600 mm(宽)×850 mm(高)。试验模型尺寸如图2所示。

图2 试验模型尺寸(单位：mm)

路基土体是将湿润状态下的稻城砂在最佳含水量下压实而成，密实度D=95%。背后填土采用膨润土混合硅砂制成，密度ρt=1.767 g/cm3。另外，在挡土墙与背面地盘之间设有促进排水的砾石层(鹿岛硅砂8～12号)。表1为试验模型所用的材料及物性。其中，砌石的力学性能通过单轴压缩试验得到，砾石层和各土体材料的力学性能通过三轴压缩试验测得。

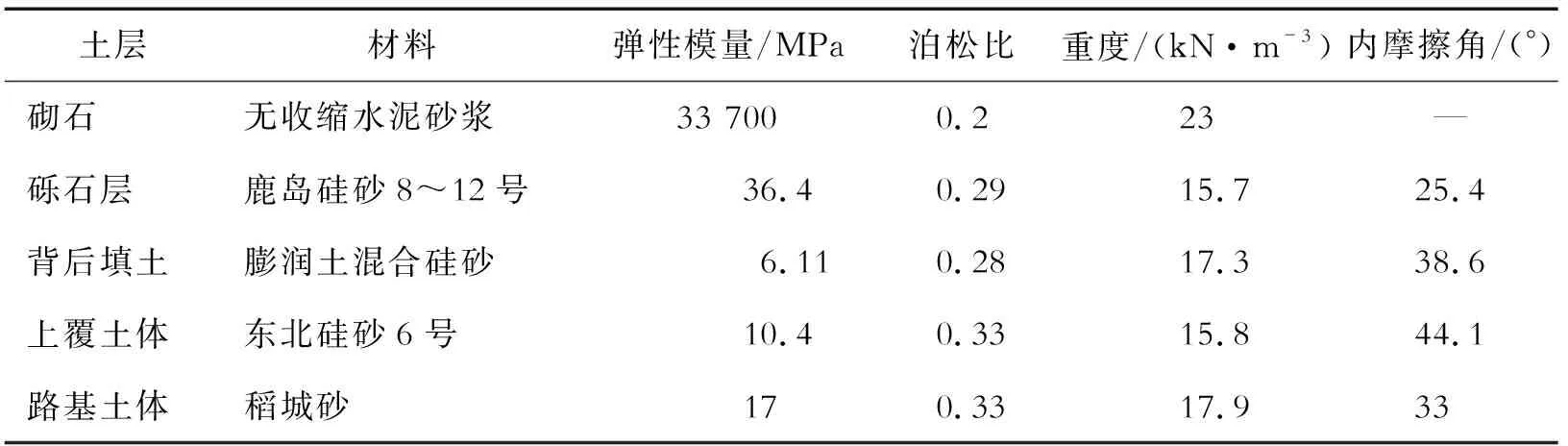
表1 材料物性

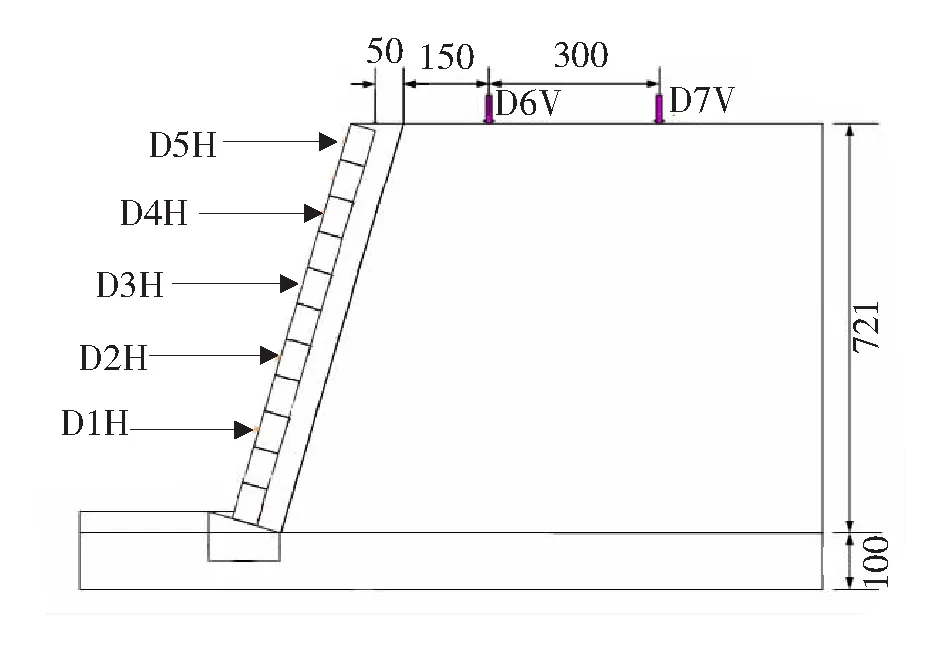
图3 位移传感器位置示意图(单位：mm)

1.3 试验加载方案

进行倾斜加载之前，在填土表面以均布荷载的形式施加上覆土体压力，大小为1 kPa。倾斜时，加载箱使作用力朝向砌石墙的前方增加，以1°/min的速度均匀加载，直到挡土墙结构出现塌陷或者土体出现大角度渗漏时，加载结束。加载过程中通过安装在挡土墙上的位移传感器对挡土墙及背后土体的变形情况进行实时监测，图3为其安装位置。

2 有限元模型的建立

2.1 建立几何模型

使用ABAQUS软件进行有限元分析时，首先需建立挡土墙的几何模型。通常来说，挡土墙沿纵向的长度远大于横截面各尺寸，且横截面大小和形状沿纵向不变，因此可将挡土墙的稳定分析视为平面应变问题。二维挡土墙模型尺寸与试验一致，砌石墙及各土层采用四节点双线性平面应变四边形单元(CPE4R)，刚性加载板采用两节点平面线性梁单元(B21)。建立三维模型时，为简化模型便于计算，取半结构进行模拟，即纵向取试验模型尺寸的一半，为300 mm，砌石及各土层采用八节点六面体单元(C3D8R)，刚性加载板采用四节点壳单元(S4R)。二维、三维有限元模型见图4。

图4 有限元模型图

2.2 定义本构关系

既有挡土墙的背后填土为膨润土混合硅砂，土体性质较差。考虑到土体材料的本构关系对还原试验的影响，背后填土采用Mohr-Coulomb弹塑性本构，其内摩擦角为38.6°，膨胀角为8.6°，粘着力为8.9 kPa。其余材料均采用线弹性本构。

图5 接触面位置

2.3 定义接触设置

实际工程中，砌石与砌石之间、挡土墙与砾石层之间、砾石层与背后填土之间等多个位置存在相互作用，而ABAQUS不能自动检测接触，故建立有限元模型时，选用了面对面离散方法(surface-to-surface discretization)在模型的特定位置设置接触对，具体位置如图5所示。

由于ABAQUS/standard中使用严格的主-从接触算法：从表面的节点不能穿透到主表面，但主表面的节点可以穿透到从表面，故选择接触对的主从表面时，遵循以下原则：

(1)刚度较大的面作为主表面；

(2)两接触面刚度相似的情况下，选网格较粗的面作为主表面；

(3)若两接触面面积不同，选取面积较大的面为主表面。

2.4 施加边界条件及载荷

由于三维模型取半结构进行计算，故对称面上的节点设置对称边界条件，即约束z向的平动自由度及绕x、y2个方向的转动自由度，模型正面的节点约束z向的平动自由度。

二维、三维模型的加载方式相同，为方便施加荷载，定义Step-1和Step-2 2个分析步。Step-1对模型施加自重，同时在背后填土的表面以均布荷载的形式施加上覆土体压力，大小为1 kPa；Step-2对加载板施加倾斜荷载，使其以1°/min的速度绕Z轴均匀转动。

图6 倾斜加载示意图

从Step-1过渡到Step-2时，为防止结构由静定结构突变为非静定结构，将加载板分为Ⅰ、Ⅱ 2部分(如图6所示)：Ⅰ部分刚度较小，能够产生弯曲变形，在保证结构静定的前提下，可模拟倾斜荷载施加的过程；Ⅱ部分刚度较大，用来模拟加载箱，以真实还原试验。Step-2的具体加载方式见图6：A、B两点铰支，在C点分别施加X方向和Y方向的强制位移，Ⅱ部分由于刚度较大不会发生变形，故绕B点整体转动，导致Ⅰ部分发生弯曲变形，从而实现倾斜加载。

3 试验结果与数值模拟对比分析

3.1 试验结果分析

倾斜试验的水平震度，如公式(1)所示，根据倾斜角θ来计算。水平震度kh较小时，墙面的水平位移逐渐增加；倾斜至7.35°时，水平震度为kh=0.13，此时水平位移急剧增加，最终导致挡土墙崩塌。墙体倒塌前，最大位移出现在墙体中间部，为8 mm，而墙顶的位移量相对较小，原因是随着倾斜角度增加，墙后的砾石下沉，背面变成空心，因此砌石失去反作用力并向后方倾倒，但背后填土未产生明显滑裂面。图7(a)给出了挡土墙崩塌前砌石的凸起情况，图7(b)给出了崩塌前墙面的变形情况。

图7 挡土墙崩塌前的情况

由上述分析可知，随着倾斜角的上升，砾石层的土压在墙体前方起作用，墙体中间部分的凸起逐渐增加；墙后填土自立性较高，在墙体与土体之间产生缝隙，只有砾石下沉；由于砾石下沉后对墙体中间的作用会增加，砌石凸起更加明显，直至倒塌。

3.2 试验与数值模拟对比分析

倾斜试验测得的水平位移是达到某倾斜角度θ时墙面产生的变形量。图8为沿墙高方向的不同高度处测点的荷载-位移曲线。

图8 不同高度处测点的荷载-位移曲线

试验数据显示，测点水平位移随着挡土墙倾斜角度的增大而逐渐增加，达到破坏角度时，墙体中间测点D3、D4的水平位移为7.5～8 mm，上部测点D5的水平位移6 mm左右，下部测点D2不足5 mm，底部测点D1则更小，几乎未产生变形。

模拟数据显示，二维、三维有限元模型的破坏角度分别为7.4°和7.7°，与试验的崩塌角度7.35°十分相近。随着倾斜角度增大，测点的位移也逐渐增加，此变化趋势与试验一致；达到破坏角度时，墙体产生较大变形，砌石之间的相互作用发生改变，导致计算不收敛，表明挡土墙达到失稳状态。

荷载-位移曲线表明，挡土墙模型破坏之前，各测点的试验数据、二维模拟及三维模拟无论从破坏角度还是墙面的水平位移，都拟合较好，位移曲线的变化趋势也十分一致，证明了有限元模拟挡土墙倾斜试验的可靠性。

4 二维、三维模型数值模拟对比分析

4.1 砌石间的接触压强

接触压强是节点上因接触而产生的单位面积的压力，是分析接触问题的一个重要指标。图9为模型破坏时砌石之间的接触压强，图9中，黑色部分表示接触压强接近于零(小于1×10-5MPa)的位置，即上下两砌石已脱开或即将脱开，灰色表示接触压强不为零的位置。观察云图可知，无论二维还是三维模型，挡土墙下部砌石之间的接触压强均为靠近填土一侧区域大，远离填土一侧区域小，且最大接触压强均出现在最底部接触面的左侧；中部砌石之间的接触压强则靠近填土一侧区域高于远离填土一侧区域，并且高接触压强区域面积较少。

干砌的砌筑方式使加载过程中挡土墙重心偏移，故倾斜加载前，由于仅受重力作用，各接触面上靠近墙后填土一侧的接触压强较大，而远离填土一侧的接触压强较小，且接触面上的接触压强呈沿墙高从上到下越来越大的趋势。倾斜加载使背后填土产生较大变形，且变形沿墙高呈非线性分布，中间填土变形较大，上下两侧变形相对较小。填土产生的变形作用于挡土墙，使砌石间的接触压强重新分布，下部砌石之间的接触面靠近填土一侧的接触压强减小，远离填土一侧的接触压强增大，最终如图9所示。

图9 砌石之间的接触压强

图10 下侧3个接触面最左侧节点的接触压强

图10给出了下侧标号为1、2、3的3个接触面(标号见图5)最左侧节点的接触压强随时间的变化曲线，横轴表示倾斜加载的时间，纵轴表示节点的接触压强。从图中各节点接触压强的二维(2D)、三维(3D)对比曲线可以看出，采用二维和三维进行模拟，接触压强的数值和变化趋势十分一致。最下侧接触面(1号)左侧节点的接触压强最大，随着接触面高度的增加，接触压强减小，4号接触面该接触压强减小为零，故未在图中显示。

4.2 背后填土等效塑性区

图11给出了二维、三维挡土墙模型加载至破坏时，背后填土的等效塑性应变区。由于受到倾覆力矩的作用，挡土墙模型倾斜加载至某一角度时，背后填土进入塑性区。二维、三维模型分别加载至4.84°、5.14°时，背后填土塑性区出现，两者出现位置相同，均为填土的左下角。继续加载，等效塑性区有向填土后方延伸成滑移面的趋势。三维挡土墙模型加载至7.72°时模型破坏，塑性应变最大值如图11(b)所示。二维挡土墙模型加载至7.4°时模型破坏，塑性应变最大值位置与三维相同。从塑性区出现到挡土墙模型破坏这一过程，随着等效塑性区的发展，等效塑性应变迅速增长，表明挡土墙模型逐渐失稳，这与荷载-位移曲线所表现的趋势一致。

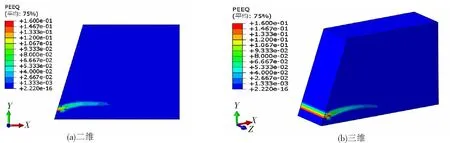
图11 背后填土等效塑性区

4.3 背后填土剪应力

由图12可知，二维、三维挡土墙模型背后填土剪应力的分布基本一致；两者剪应力的最大值分别为9.746e-2 MPa、9.951e-2 MPa，相差2%左右，出现位置均为靠近墙体一侧的下方。靠近基础的区域，背后填土剪应力较大，且同一深度处，靠近墙体一侧土体的剪应力大于远离墙体一侧土体。沿墙高方向，土体的剪应力越来越小，这是由于挡土墙在向背离填土方向倾斜的过程中，墙后填土有沿着墙背下滑的趋势。

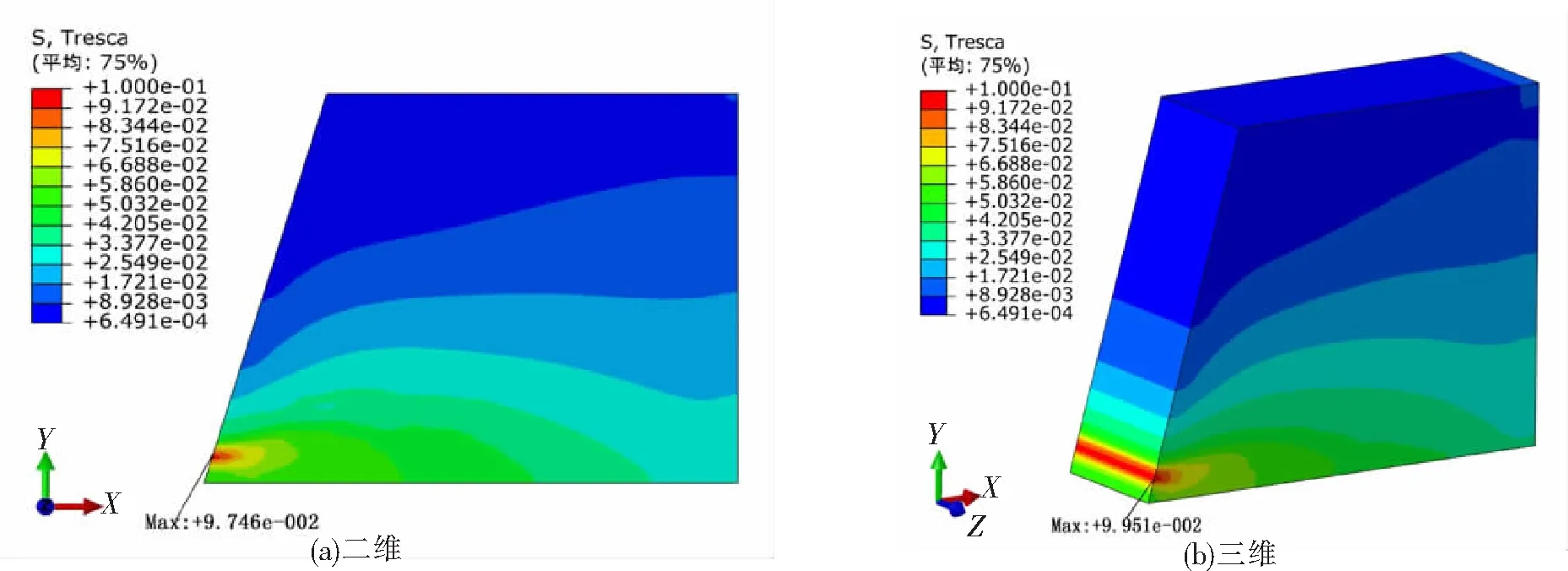
图12 背后填土剪应力分布

4.4 计算效率

表2给出了二维、三维模拟的计算时长和模型中接触单元的数量。由表2可以看出，从开始倾斜加载至模型破坏，三维模型计算时长是二维的11.5倍，而由上述分析可知，两者达到的模拟效果相近，故在相同计算精度下，二维模拟能够缩短计算时长，提高计算效率。同时，接触单元过多会造成ABAQUS有限元软件数值计算上的不稳定，二维模型有245个接触单元，而三维模型有3 900个接触单元，是二维的16倍。二维模型大幅度减少了接触单元的数量，使计算更稳定更易收敛。

表2 计算时长和接触单元数

5 结论

通过对某公路砌石挡土墙模型试验及数值模拟分析，可以得到以下结论：

(1)通过对比分析试验数据和有限元数据，阐述了挡土墙结构的破坏过程，探究了挡土墙破坏机制，可以为今后挡土墙的加固和抗震提供更好的设计基础。

(2)倾斜试验中，水平震度kh达到0.13时，挡土墙破坏。加载过程中，随着倾斜角的增大，墙体与土体之间产生缝隙，砾石下沉，且由于砾石下沉后对墙体中间部位的作用增加，砌石凸起更加明显，同时墙面缺乏整体性，最终导致挡土墙坍塌破坏。

(3)二维和三维数值模拟得到的破坏角度(7.4°和7.7°)均接近于试验破坏角度(7.35°)，测点水平位移也较为一致;其次，二维、三维模拟得到的荷载-位移曲线、砌石间的接触压强、背后填土塑性区和剪应力分布相当一致，说明研究挡土墙的抗震稳定性问题时，二维模型能够达到三维模型的效果。

(4)二维模拟具有较高的计算效率，且能够有效克服由于接触单元过多带来的不收敛问题，使计算过程更加稳定。