中低应变加载速率下单节理裂隙岩体的单轴动态压缩力学性能试验

(1.华东交通大学 土木建筑学院, 江西 南昌 330013; 2.浙江省工程勘察院，浙江 宁波 315000)

0 引言

应变率对岩石等材料动态力学性质的显著影响，一直是研究的热点。一般认为，应变速率小于 10-4s-1属于低应变速率(属静态加载)，10-4～10-2s-1属于中等应变速率(属准动态加载)，大于10-2s-1属于高应变速率(属动态加载)。

实际岩土工程中，岩石边坡或者隧道的长期蠕变均属于中低应变加载速率条件下的力学行为。因此，针对岩石开展中低应变加载速率下的力学特性试验研究具有重要意义。

Meng et al[1]对不同尺寸的岩石试件进行了中低应变加载速率下的单轴压缩试验，低应变加载速率设置为1.0×10-5s-1、5.0×10-5s-1、1.0×10-4s-1、5.0×10-4s-1、1.0×10-3s-1和5.0×10-3s-1；Liang et al[2]对花岗岩试件进行了中低应变加载速率下的单轴压缩试验，低应变加载速率范围为1.0×10-5～1.0×10-2s-1；Liang et al[3]对盐岩试件进行了中低应变加载速率下的单轴压缩试验，低应变加载速率设置为2.0×10-5s-1、2.0×10-4s-1和2.0×10-3s-1；Wasantha et al[4]对不同大小颗粒的砂岩试件进行了中低应变加载速率下的单轴压缩试验，低应变加载速率设置为10-6s-1、10-5s-1、10-4s-1和10-3s-1； Tang et al[5]对石灰岩试件进行了低、中和高应变加载速率下的单轴压缩试验，低应变加载速率范围为1.1×10-5～1.1×10-1s-1；Fahimifar et al[6]对花岗岩试件进行了中、高应变加载速率下的三轴压缩试验，应变速率设置为10-4s-1、10-3s-1、10-1s-1和100s-1。

Liu et al[7]对砂岩进行了高应变加载速率下的单轴压缩试验，在试验中设置了5种冲击速度；Hokka et al[8]对花岗岩进行了高应变加载速率下的单轴压缩试验，应变加载速率范围为1.0×10-6～600 s-1；Yin et al[9]对煤岩进行了高应变加载速率下的单轴压缩试验；Zou et al[10]对大理岩进行了高应变加载速率下的单轴压缩试验；Liu et al[11]对煤岩进行了低应变加载速率下和高应变加载速率下的单轴压缩试验。

根据应变加载速率的设置范围，可将文献[1]～文献[4]的试验归为中低应变加载速率下的压缩试验，将文献[5]～文献[11]的试验归为高应变加载速率下的压缩试验。

实际上，岩石往往会存在节理，而节理面的倾角也会影响节理岩体试件的动态力学特性，上述只有Fahimifar et al[6]和Liu et al[11]研究了节理面或者层理面的倾角对试件动态力学特性的影响。但是，Fahimifar et al[6]只考虑了节理面倾角为30°、45°和60°，Liu et al[11]只考虑了层理面倾角0°和90°。因此，有关节理岩体的动态力学特性试验成果还相对比较少，已有的研究成果中考虑节理面或者层理面的倾角影响也较少。

因此, 本研究将对不同节理面倾角 (0°、15°、30°、45°、60°、75°和 90°) 的人工节理岩体试件进行中低应变加载速率(10-5s-1、 10-4s-1、 10-3s-1、 10-2s-1和10-1s-1) 下的单轴压缩变形试验，研究节理面倾角和应变加载速率对节理岩体试件的动态压缩力学特性和损伤变量演化规律的影响。

1 试验原理

1.1 试件制作

图1 荷载方向与节理面间的几何关系

试件尺寸为70.7 mm×70.7 mm ×70.7 mm，预制节理由厚度为1 mm的木板形成。如果连通率太小，可能节理裂隙倾角对试件整体力学性能的影响比较小。因此，节理的宽度设置为5.66 cm，连通率为80%。定义节理面与轴向荷载作用平面(水平面)间的夹角为β。节理岩体模型的加载示意如图1所示。

试件采用水灰比为0.65的水泥砂浆倒入模具中浇铸而成。试验中所用水泥的强度等级为42.5 MPa，砂采用厦门艾思欧标准砂有限公司生产的标准砂，粒径范围为0.5～1.0 mm，为中级标准砂。胶砂比为1∶2，水灰比为0.65。待水泥砂浆初凝后，依照图1中的短线位置插入相应宽度的木板，木板的长度为10 cm，木板永久留在试件中。试件的强度与千枚岩等软弱岩石的强度比较接近。本文暂且没有按一定相似比，来配制与千枚岩相似的岩石试件。

1.2 试验顺序

试件经标准养护28 d后，并放置7 d，然后将试件放在WAW-600C万能压缩变形试验机上进行单轴压缩变形试验。在进行单轴压缩变形试验时，加载的应变速率包含4种，即分别为10-2s-1、10-3s-1、10-4s-1和10-5s-1。

采用各种节理面倾角的节理岩体试件进行每种应变率下的单轴压缩试验时，都是采用3个试件进行试验。在后文对单轴抗压强度进行分析时，通常是3个试件的抗压强度的平均值，但当其中有1个试件的抗压强度与平均抗压强度间的差值超过平均值的15%，则该试件的抗压强度不予采用，将采用其他2个试件的抗压强度的平均值。

2 试验结果与分析

2.1 应力应变曲线的变化

当加载的应变速率相同时，节理面倾角对试件的应力应变曲线的影响见图2。

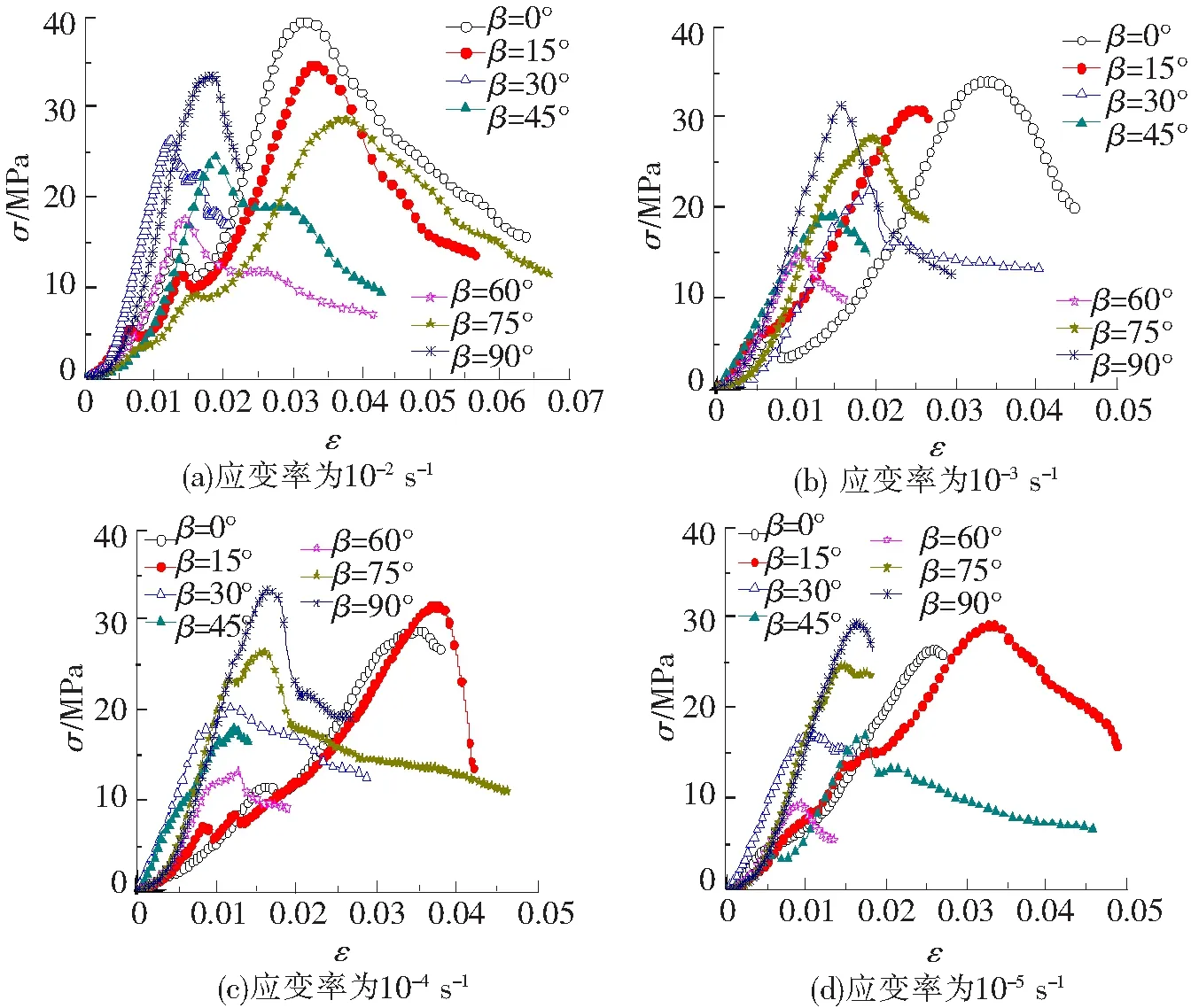
图2 加载的应变率相同时节理面倾角对试件的应力应变曲线的影响

当加载的应变速率相同，β由0°增加到90°时，试件的峰值应力呈逐渐减小后又逐渐增加的趋势，当β为60°时试件的峰值应力最低。

当试件的节理面倾角β相同时，随着应变加载速率由10-5s-1增加到10-2s-1，试件的峰值应力呈逐渐增加的趋势。

2.2 抗压强度的变化

当加载的应变速率相同时，节理面倾角对试件的强度影响见图3。当试件的节理面倾角相同时，试件的强度随应变加载速率的变化规律见图4。

图3 应变率相同时节理面倾角对强度的影响

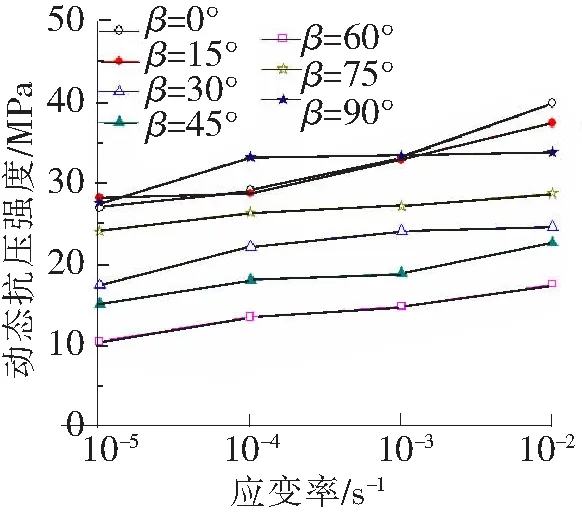
图4 节理面倾角相同时应变率对强度的影响

当加载的应变速率相同时，随着β由0°增加到90°，试件的抗压强度呈逐渐减小后又逐渐增加的趋势，当β为60°时试件的抗压强度最低。

当试件的节理面倾角β相同时，随着应变加载速率由10-5s-1增加到10-2s-1，试件的抗压强度呈逐渐增加的趋势。

节理岩体试件的动态强度增长因数DIF的表达式为[12]

DIF=fcd/fcs

(1)

式中，fcd为当前应变率下节理岩体的极限抗压强度；fcs为拟静态应变速率下节理岩体的极限抗压强度，本文的拟静态应变速率取为10-5s-1。

动态强度增长因数DIF和当前应变速率之间的关系可采用线性表达式[12]

图5 节理岩体的动态增长率与应变率的关系

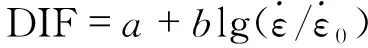
(2)

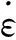
节理岩体试件的动态强度增长因数DIF随应变率的变化规律见图5。

节理岩体试件强度增长因素的结果分别见式(3)～式(9)。

β= 0°：

(3)

β= 15°：

(4)

图6 试件的b值随节理面倾角的变化规律

β=30°：

(5)

β=45°：

(6)

β=60°：

(7)

β=75°：

(8)

β=90°：

(9)

试件的b值随节理面倾角的变化规律见图6。

由图6可知，当β为60°时试件的b值最大，说明当β为60°时试件的抗压强度对应变率敏感性最强，即强度低的节理岩体试件的强度对应变率的敏感性最强。

2.3 峰值应变的变化

当应变速率相同时，节理面倾角对试件的峰值应变的影响见图7。当试件的节理面倾角相同时，试件的峰值应变随应变加载速率的变化规律见图8。

图7 应变率相同时节理面倾角对峰值应变的影响

图8 节理面倾角相同时应变率对峰值应变的影响

当应变加载速率相同，随着β由0°增加到90°，试件的峰值应变均呈先减小后略有增加的变化规律；当应变加载速率为10-2s-1时，β为30°时试件的峰值应变最小，当应变加载速率为10-3s-1时，β为60°时试件的峰值应变最小，当应变加载速率为10-4s-1，β为45°时试件的峰值应变最小，当应变加载速率为10-5s-1时，β为60°时试件的峰值应变最小。

当节理面的倾角相同时，试件的峰值应变随应变加载速率的变化并没有固定明显的变化规律。

2.4 弹性模量的变化

弹性模量数值取50%峰值应力对应的应变计算出的割线弹性模量[13]。当应变加载速率相同时，节理面倾角对试件的弹性模量的影响见图9。当试件的节理面倾角相同时，试件的弹性模量随应变加载速率的变化规律见图10。

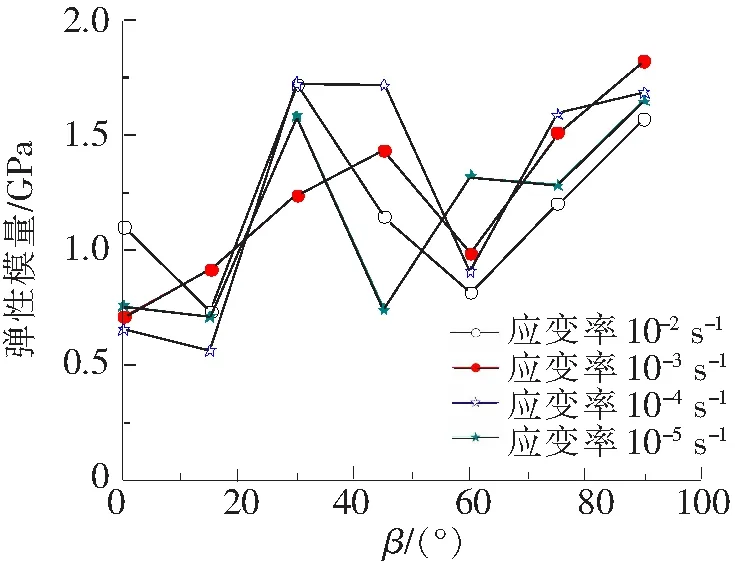
图9 应变率相同时节理面倾角对弹性模量的影响

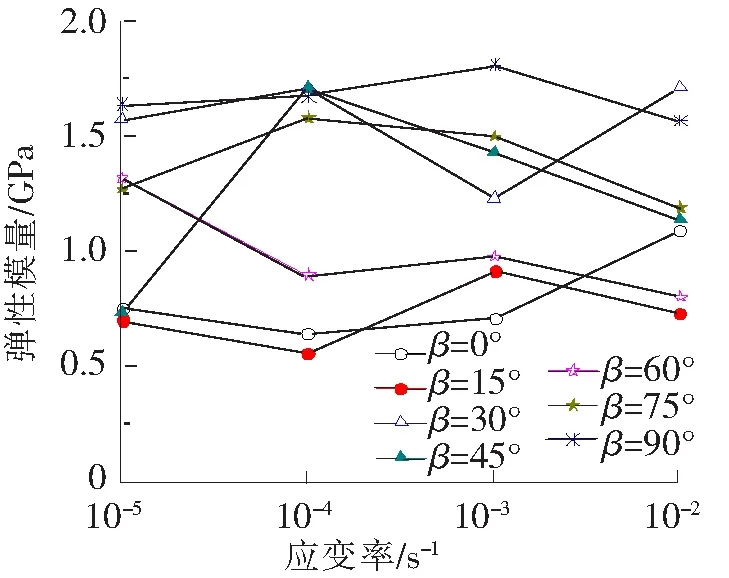
图10 节理面倾角相同时应变率对弹性模量的影响

当应变加载速率相同，随着β由0°增加到90°，试件的弹性模量的变化幅度比较大，虽然并非呈一直增加的趋势，中间会出现减小的变化规律，但整体呈逐渐增加的变化规律。

当节理面的倾角相同时，试件的弹性模量随应变加载速率的变化并没有固定明显的变化规律。

3 节理岩体试件的损伤变量的演化

3.1 损伤变量的演化方程

根据 Lemaitre 的应变等价性假说，损伤对应变行为的影响通过有效应力来体现，即名义应力作用在损伤材料上产生的应变与有效应力作用在无损材料上产生的应变相等，该假说在一维应力状态下可用式(10)表示[14-16]

σ=Eε(1-D)

(10)

式中，σ为应力；ε为应变；D为损伤变量。

由于岩石微元强度服从Weibull分布，因而可认为材料的损伤参量D也服从该统计分布，可以得到基于Weibull分布函数的损伤变量[14-16]

(11)

式中，ε为应变；m和n为统计参数。

图11 完整试件的应力应变曲线

经过推导可以得到试件的损伤变量的演化方程为[14-16]

(12)

(13)

式中，σm为峰值应力;εm为峰值应力σm。

根据式(13)，要计算得到m，需要得到完整试样未含节理面时的弹性模量E0，对水灰比为0.65的试件(尺寸为7.07 cm×7.07 cm×7.07 cm)进行了应变加载速率为10-5s-1时的单轴压缩变形试验，试件中未含节理，应力应变曲线如图11所示。完整试件的弹性模量取50%峰值应力对应的应变计算出的割线弹性模量，从而得到完整试件在加载速率为10-5s-1时的弹性模量E0为2.652 GPa，代入式(13)可得到不同节理面倾角的试件的m值。

针对图2给出的代表性试样的应力应变曲线，先计算得到它们的m和εm值，见表1，再计算得到这些试样受荷载的损伤变量D的演化曲线。

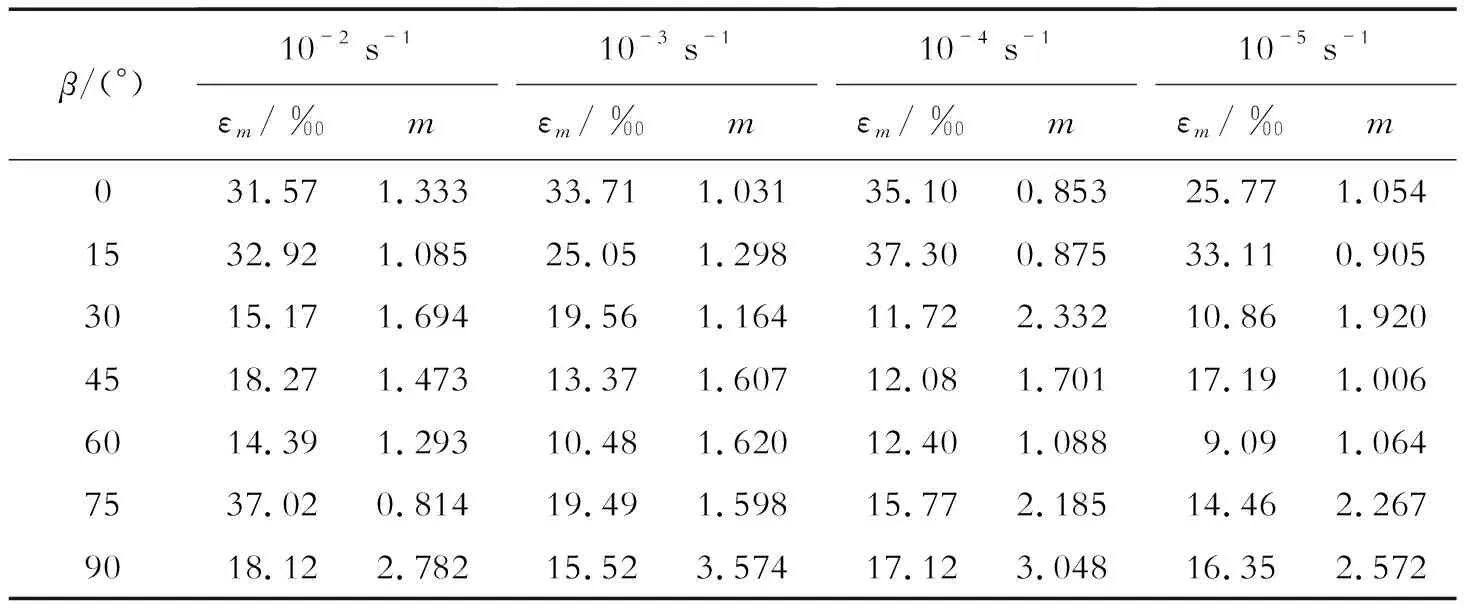
表1 图2所示的代表性试样的m和εm值

3.2 节理岩体试件的损伤变量的演化

当试件的应变加载速率相同时，节理面倾角对试件的损伤变量的影响见图12。

图12 应变率相同时节理面倾角对损伤变量的影响

当应变加载速率相同和应变相同时，随着节理面的倾角由0°增加到60°，损伤变量D基本都呈逐渐增加的趋势，随着节理面的倾角由60°增加到90°，损伤变量D基本都呈逐渐减小的趋势，当节理面倾角为60°时的损伤变量最高，当节理面倾角为90°时的损伤变量最小。当节理面倾角为60°时损伤变量达到最大值，这是由于当节理面倾角60°时，节理岩体试件内部的微裂纹更容易扩展，而当节理面倾角为90°时，相比其他节理面倾角的情况，节理岩体试件内部的微裂隙相对较少，损伤程度较低。

当试件的节理面倾角相同时，应变率对试件的总损伤变量的影响见图13。

图13 节理面倾角相同时应变率对总损伤变量的影响

当试件的节理面倾角相同时，应变加载速率由10-2s-1增加到10-5s-1，损伤变量基本呈逐渐增加的趋势。主要由于应变加载速率越小时，试件内部的微裂隙更容易扩展演化。

4 结论

(1) 当加载的应变速率相同，随着β由0°增加到90°，试件的抗压强度呈逐渐减小后又逐渐增加的趋势，当β为60°时，试件的抗压强度最低；当试件的节理面倾角β相同时，随着应变加载速率逐渐增加，试件的抗压强度呈逐渐增加的趋势；当β为60°时，试件的抗压强度对应变率敏感性最强，说明强度低的节理岩体试件的强度对应变率的敏感性最强。

(2) 当应变加载速率相同，随着β由0°增加到90°，试件的峰值应变均呈先减小后略有增加的变化规律；当节理面的倾角相同时，试件的峰值应变随应变加载速率的变化并没有固定明显的变化规律。

(3) 当应变加载速率相同，随着β由0°增加到90°，试件的弹性模量整体出现逐渐增加的变化规律；当节理面的倾角相同时，试件的弹性模量随应变加载速率的变化并没有固定明显的变化规律。

(4) 当应变加载速率相同，且应变相同时，随着节理面的倾角由0°增加到60°，损伤变量D基本都呈逐渐增加的趋势，随着节理面的倾角由60°增加到90°，损伤变量D基本都呈逐渐减小的趋势，当节理面倾角为60°时，损伤变量最高，当节理面倾角为90°时，损伤变量最小。

(5) 当试件的节理面倾角相同时，随着应变加载速率逐渐增加，损伤变量基本呈逐渐增加的趋势，主要由于应变加载速率越小时，试件内部的微裂隙更容易扩展演化。