负弯矩作用下钢-混凝土组合梁截面受力性能分析

22

(1.石家庄铁道大学 土木工程学院，河北 石家庄 050043；2.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室，河北 石家庄 050043)

0 引言

连续钢-混凝土组合梁桥在负弯矩区处于混凝土顶板受拉、钢梁受压的不利受力状态，混凝土受拉开裂后会导致组合梁刚度和耐久性降低，同时钢梁受压易导致局部屈曲的出现。因此，混凝土顶板的开裂和钢梁的屈曲问题始终制约着连续组合梁的发展。20世纪80年代，钢-混凝土双面组合梁(简称双面组合梁，DCB)的出现明显改善了钢梁受压腹板和翼缘的屈曲问题[1-3]，但由于截面中性轴的下降，混凝土顶板仍易受拉开裂[4]。为了改善混凝土顶板的抗裂性能，段树金等[5]在双面组合梁的基础上提出了钢-混凝土组合与叠合梁结构(简称组合与叠合梁，CLB)，其中混凝土顶板与钢梁上翼缘用抗拔不抗剪连接件[6]连接形成叠合界面，有效地释放了混凝土板中因收缩徐变、温度效应以及汽车荷载引起的拉应力，并且提高了负弯矩区桥面板纵向预应力的施加效率，实现了纵向的自由滑移，同时保留了竖向的抗掀起作用。组合与叠合梁不同于传统中的叠合梁，抗拔不抗剪连接件使得混凝土板与钢梁在保证竖向变形一致即不发生掀起的前提下能够自有变形。

工程现场实测和有限元分析结果[7]表明：组合与叠合梁能有效提高连续组合梁负弯矩截面以及结构的刚度、调整结构的内力、改善结构的受力性能[8]。目前，组合与叠合梁的研究尚处于起步阶段，相关的研究文献也比较少，因此，对组合与叠合梁展开系列研究显得尤为迫切。为比较普通组合梁(CCB)、双面组合梁和组合与叠合梁的受力性能，采用截面全过程分析法对这3种形式的组合梁截面的弯矩曲率关系、各阶段的弯曲刚度进行分析，并对梁的最大裂缝宽度进行计算，以得到这3种组合梁截面不同的受力特性。

1 截面全过程分析

在对钢筋混凝土构件进行受力性能分析时，裂缝的出现、开展，挠度或转角的增长以及弹、塑性极限状态等的分析对结构的应用和研究起着至关重要的作用，而截面的全过程分析法是研究这些问题的基础。图1给出了普通组合梁、双面组合梁和组合与叠合梁的截面构造图，本节以普通组合梁为例，对负弯矩作用下截面的受力全过程进行分析。

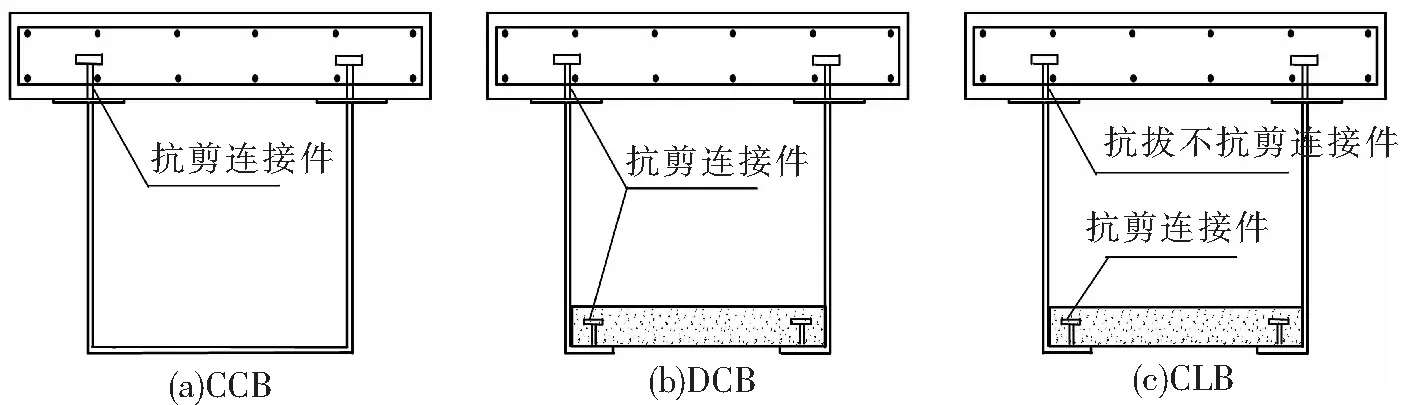
图1 截面构造图

截面的全过程分析是对截面的内力随着中性轴的变化、曲率的增长，以及受力过程中材料应力(应变)和失效，加之混凝土裂缝的开展等进行分析的方法。在分析过程中，对截面进行条带划分，对受力全过程进行分级、逐步的运算。

1.1 基本假定

(1)结构从开始受力到破坏整个过程，符合平截面假定。

(2)构件的变形很小，不考虑变形对计算图形和内力值的影响。

(3)混凝土应力-应变关系[9]如图2(a)所示。

(1)

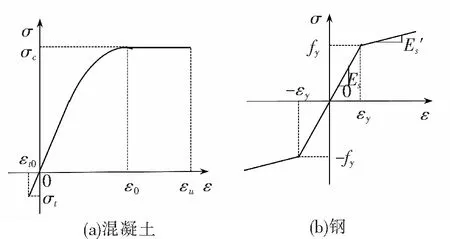
图2 组合梁截面计算图形

σt=Ecεt(εt≤εt0)

(2)

式中,σc、σt分别为混凝土的压、拉应力；fc为混凝土轴心抗压强度；ε0为混凝土峰值压应变，混凝土强度等级不大于C50时，取值0.002；εcu为混凝土极限压应变，混凝土强度等级不大于C50时，取值0.003 3；n为系数，n≤2，本文取值为2；εt为混凝土拉应变；εt0为混凝土峰值拉应变。

(4)钢的应力-应变关系采用考虑硬化的弹塑性关系[9]，如图2(b)所示，其中，fy为钢的屈服强度；εy为屈服应变，εy=fy/Es；Es′=0.01Es。

图3 组合梁截面计算图形

1.2 基本方程

在截面全过程分析中，基于以上基本假定，可以建立3类基本方程：几何方程、物理方程和力学(平衡)方程。分析中不考虑开裂受拉混凝土的强度和组合界面滑移的影响。在进行截面条带划分时，对混凝土板、钢筋、钢梁分别进行条带划分，并假定每一条带上的应力、应变均匀分布。组合梁截面的计算图形如图3所示。

依据平截面假定，当构件受载后，其应变分布如图3所示。弹性阶段，随着截面曲率的增长，普通组合梁、双面组合梁和组合与叠合梁截面的中性轴位置保持不变。当普通组合梁的受压钢梁翼缘达到屈服应变εy时，截面进入弹塑性阶段。在双面组合梁和组合与叠合梁中，当钢梁下翼缘受压达到屈服应变εy或混凝土底板压应变达到ε0时，截面进入弹塑性阶段。荷载继续增大，当普通组合梁、双面组合梁的受拉钢筋、组合与叠合梁的钢梁受拉翼缘达到各自的屈服应变εy时，截面进入塑性状态。由于组合与叠合梁的上层混凝土板和下层钢梁分别作用，因此，上层混凝土板的受力全过程分析可参照钢筋混凝土构件进行。

1.2.1 几何方程

沿梁截面轴线单位长度的相对转角φ(截面曲率)为

(3)

式中，εst、εsc分别为钢梁受拉翼缘和受压翼缘的应变，如图3所示；hs为钢梁的高度。

距离中性轴yi处的应变为

(4)

yi>0，εst为正；yi<0，εst为负。

1.2.2 物理方程

对受拉或受压的钢筋、钢梁和混凝土采用基本假定中的应力-应变关系。

εi为正，材料受拉；εi为负，材料受压。

(5)

1.2.3 力学(平衡)方程

负弯矩作用下，组合梁的受力平衡条件为

∑Ni=0,∑Mi=M

(6)

1.3 M-φ曲线计算程序

综合以上3类基本方程，可以得出式(6)中只有2个未知量，即φ和h0(中性轴高度)。通过合理选取步长Δφ，来满足计算精度或节省计算工作量的要求。具体计算程序如下：

(1)φi+1=φi+Δφ，φ1=0；

(2)根据力学(平衡)方程，得出截面中性轴的高度h0；

(3)由中性轴位置h0和相对转角φi得到每个条带的应变；

(4)判断每个条带的应变是否达到相应材料的极限应变，若没有则进行以下程序，若已经达到材料的极限应变，停止计算；

(5)通过材料的应力-应变关系得到每个条带的应力，并通过数值积分得到外荷载M；

(6)由一一对应的φ值和M值得到M-φ曲线。

在截面受力全过程分析中，混凝土的开裂、钢梁和钢筋的屈服、极限状态等阶段均应控制步长，以满足分析的准确性。

2 工程算例

为深入研究不同形式钢-混凝土组合梁截面的受力性能，本节以某双面组合梁工程实例为背景，通过截面刚度、M-φ曲线和梁的最大裂缝宽度，比较双面组合梁(DCB)、无混凝土底板的普通组合梁(CCB1)、钢底板厚30 mm的普通组合梁(CCB2)及改变连接形式的组合与叠合梁(CLB)的受力性能差异。该双面组合梁的截面如图4所示。

图4 双面组合梁截面图(单位：mm)

材料参数：钢梁为Q345qD钢，屈服强度fy=345 MPa，弹性模量Es=206 GPa；纵向钢筋为HPB300钢筋，fr=300 MPa，弹性模量Er=206 GPa，直径Φ20；混凝土顶、底板强度等级为C40，fc=26.8 MPa，ft=2.39 MPa，Ec=32.5 GPa。

2.1 M-φ曲线

对上述4种截面进行受力全过程分析，得到相应的M-φ曲线，如图5所示。

图5 M-φ曲线

从图5中看，DCB、CLB和CCB2的极限弯矩相当，而CCB1的极限弯矩只有其他截面的一半左右。从局部放大图中容易得到4种组合梁截面开裂弯矩的大小。其中，CCB1的开裂弯矩最小；DCB与CCB2的开裂弯矩几乎相等且大于CCB1；CLB的开裂弯矩最大，为其他截面的2～3倍。

2.2 刚度分析

基于换算截面法得到4种组合梁截面的初始刚度及混凝土顶板开裂后的刚度[4,7]，如表1所示。

表1中，DCB初始刚度比CCB1提高了70%左右，CLB的初始刚度约为DCB的33%，CCB2的初始刚度约为双面组合梁的85%。混凝土顶板开裂后，CCB1、CCB2、DCB刚度下降较多，而CLB刚度几乎没有降低，开裂后CCB2、DCB和CLB的刚度相当。

表1 截面刚度 MN·m2

2.3 极限弯矩

由截面全过程分析得出4种组合梁截面的开裂弯矩、弹性极限弯矩和塑性极限弯矩，结果如表2所示。

由表2，DCB与CCB1的开裂弯矩较低，CCB2的开裂弯矩有所提高，CLB的开裂弯矩较其他形式组合梁提高了1～2倍,可有效延缓裂缝的开展；CLB弹性极限弯矩与DCB相当，约为CCB1的2倍，CCB2弹性极限弯矩略低于DCB；DCB的塑性极限弯矩较CLB和CCB2提高了10%～20%，约为CCB1的2倍。

2.4 裂缝宽度分析

钢-混凝土连续组合梁负弯矩区裂缝的开展成为学者们研究的重要课题，因此采取一定的措施减缓裂缝的发展成为连续组合梁研究的重中之重。混凝土顶板与钢梁的连接程度和刚度比都对裂缝的开展有一定的影响。

文献[9]中将裂缝分为受弯、轴心受拉、偏心受拉和偏心受压裂缝，其最大裂缝宽度ωmax为

(7)

(8)

式中,αcr为构件受力特征系数，普通组合梁与双面组合梁为轴拉型裂缝，取值2.7；组合与叠合梁为弯曲裂缝，取值1.9；ψ为裂缝间纵向受拉钢筋应变不均匀系数，0.2≤ψ≤1.0；σs为钢筋混凝土构件纵向受力钢筋的等效应力；Cs为最外层纵向受拉钢筋净保护层厚度；ρte为按照受拉钢筋混凝土截面面积计算的纵向受拉钢筋的配筋率，ρte=(Ar+Ap)/Ate,Ar为普通钢筋面积，Ap为预应力钢筋面积，Ate为有效受拉混凝土截面面积，ρte<0.01时，取ρte=0.01；deq为受拉区纵向钢筋的等效直径。

根据以上计算公式，得到CCB2、DCB和CLB 3种截面的组合梁在正常使用荷载下的最大裂缝宽度，如表3所示。

由表3可知，正常使用荷载下，CCB2的裂缝宽度最大，DCB次之，CLB的裂缝宽度很小，仅为前两者的3%。

3 结论

本文用截面全过程分析法研究了钢-混凝土普通组合梁、双面组合梁和组合与叠合梁截面的受力性能和梁最大弯曲裂缝宽度。结论如下：

(1)混凝土顶板开裂后，普通组合梁(钢底板厚30 mm)、双面组合梁和组合与叠合梁的弯曲刚度相当。

(2)组合与叠合梁的开裂弯矩较普通组合梁和双面组合梁提高了1～2倍；三者的弹性极限弯矩相差不大；双面组合梁的塑性极限弯矩最大，较普通组合梁(钢底板厚30 mm)和组合与叠合梁提高了10%～20%。

(3)正常使用荷载下，组合与叠合梁的裂缝宽度仅为普通组合梁或双面组合梁的3%。