例题教学后反思的重要性
方慧君

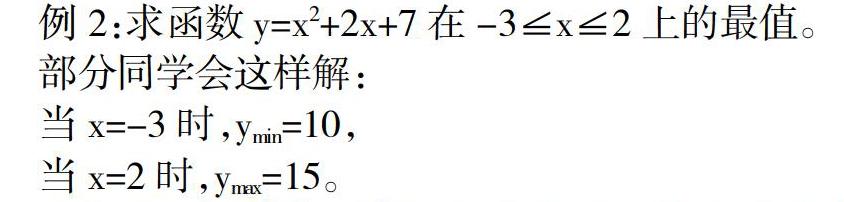
[摘 要]例题教学是课堂教学的重要环节。数学例题是知识由产生到应用的关键一步,加强各类例题教学,可以帮助学生理解和掌握基础知识,有效提高学习能力,从而达到发展智力的目的。同样,例题教学后的反思也不容忽视,它是一个知识小结、方法提炼的过程。重视例题教学后的反思,能使教师的教学更完美,更有助于学生的学习。
[关健词]例题教学;引导反思;思维
人要发展,最基本的途径有两个:一是善于探索,二是善于反思。例题教学后的反思,对提升学生的自主探究能力和创新意识有着不可估量的作用。怎样进行例题教学后反思,笔者略谈一二。
一、反思解题思路,培养学生思维的灵活性
数学教材中的每一道例题,都是某个阶段学生应掌握的具体内容。学生对于这些例题的解答,往往由于审视角度不同而采取不同的解法。在教学中,教师若能经常有意识地启发、引导学生在获得基本解题方法的基础上,通过积极反思去寻找更好、更完美的解法,不仅有利于学生联系新旧知识,还有利于培养其思维的灵活性。同时,由于学生的理解能力差异,总有一些学生对解题思路一知半解,因此教师要认真引导学生整理思维过程,确定解题思路,使解题过程清晰化,思维条理化,进一步提高学生思维的灵活性。
例1:(如图1),正方形ABCD中,E是AB的中点,BF⊥CE,垂足为F,连接DF,求证:DF=CD。
解法1:(计算法)作DG⊥CE于点G,设BC=2,则BE=AE=1,在Rt△EBC 中,利用勾股定理,可得 CE=,利用面積法可得 BF=,在 Rt△EBC中,利用勾股定理 FE=,则 GF=CE-EF=,又易证 △BFC?△CGD,可得CG=BF=,
则FG=CF-CG=,∴CG=FG∴CD=DF 得证。
反思:设数值(而不设字母)可以最大限度的简化计算量,又不影响线段关系,方法较为简便。
解法2:(计算法2)反思解法1中解题过程利用勾股定理的部分,也可以改用三角函数或者三角形相似也可以解决。(如图2)
解法3:(利用斜边中线、三线合一)
过D作DH⊥CE于点G,交BC于H,
易证 △EBC?△HCD,得CH=BE=AB= CB
即H为BC得中点,于是FH=HC,由等腰三角形“三线合一”得:FG=CG
即DH为FC的中垂线, ∴CD=DF得证。
反思解法3的过程,我们也可以先取BC中点H,进而证明DH CE,也是可行的。同时,本题也可以利用建坐标系法,或者构造适当的辅助线,利用四点共圆等性质也是可以解决,这里不做详细介绍。
通过反思,学生不仅得到了本题的多种证法,而且在讲解过程中还复习了几何中几个重要性质的用法,培养了学生善于从不同角度思考问题的习惯,进一步拓宽学生的解题思路,培养思维的灵活性,避免解题时出现解题单一、狭窄、逻辑混乱等问题,达到了很好的教学效果。
二、反思题目特征,培养学生思维的广阔性
新课程对课堂教学提出了挑战,即要构建以学习者为中心,以学生自主活动为基础的新型的教学模式;还强调发现学习和探究学习,要求教师教学后要引导学生积极反思,启发学生沟通各种知识的内在联系,解完一道题后,通过反思题目特征,将此题逐步引申或广泛联想,不仅巩固所学知识,而且培养其思维的广阔性。在平时的课堂教学中,教师要积极引导学生多角度、多方位进行思考,可对结论进行变形,对常规教学进行反思,改变其形式。这样既培养了学生理解问题和解决问题的能力,又使学生的自主学习过程成为能动的、开放的、有序的时空,更能培养思维的广阔性。
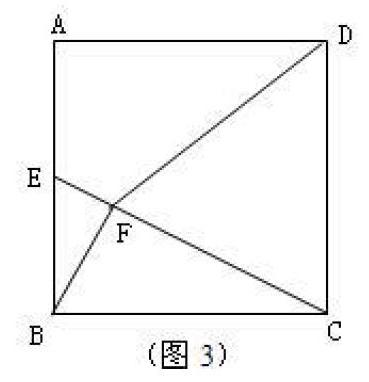
在例1中,我们可以引导学生积极思考、探讨,变换条件,从而加深他们对此题的理解。(如图3):
变式1:如图,正方形ABCD中,E是AB的中点,
F为CE上一点,且DF=CD,求证:BF⊥CE
变式2:如图,正方形ABCD中,BF⊥CE,垂足为F,DF=CD,求证:E是AB的中点。
像这样,从多个角度去引导学生,从多方位变换题中的条件与结论进行变式教学,不仅可以让学生对问题结构和特征加深理解,而且可以让学生的思维更开阔,有效提升学生分析问题和解决问题的能力。
三、反思解题方法,培养学生思维的发散性
教师要特别注意向学生介绍数学知识的产生、发展背景,要引导学生了解知识的“切入点”。解完一道题后,通过反思解题方法培养其思维的发散性。
如例1中,还可以用建坐标系法解决,这个方法将几何元素间的关系数量化,化繁为简,非常简便。在解决其它数学问题如动点问题时也可以用。很多问题的解题思路和方法相似,如能在教学中不失时机地将某些问题作适当的引申,不仅可以提高学生的学习兴趣,而且能使学生的数学学习有持续力,培养了学生思维的发散性。
四、反思解题结果的正确性,培养学生思维的批判性
反思解题结果的正确性,可以提高思维的严密性,培养学生思维的批判性。思维的批判性是指思维活动中独立分析和批判的程度,它表现为能够在解决数学问题的过程中不断地总结经验教训,进行回顾和反思,自觉调控思维的进程,及时发现错误,纠正错误。因此,在教学中,首先要指导学生经常自我诊断,品尝错解苦涩;其次,教师在课堂上不仅要传授知识,还应该担负培养学生良好学习品质的重任。
例2:求函数y=x2+2x+7在-3?x?2上的最值。
部分同学会这样解:
当 x=-3时,ymin=10,
当x=2 时,ymax=15。
类似的解题错误不胜枚举,有的显而易见,有的比较隐蔽,但是如果学生在解题后能认真地对错误进行反思,就很容易发现错误并且及时改正。这些错误与他们的心理障碍有关,也与他们在数学学习实践中方法失当、能力不足有关。因此,要对学生倾注更多的爱心,也要从教学技术层面帮助他们解决实际问题。
例如,对于例2,在教学中为了让学生发现自己的问题,我给他们举了一个反例:
当x=0时,y=7,从中可以发现结果与上面结论矛盾。接下来再让学生画出图像,从图像上看,可以发现结论错误。接着,再进行说明,证明函数的最值不可以通过取特殊值来求,必须数形结合。最后,引导学生利用函数图像求解,并对自变量范围进行变式,巩固学生对方法的理解和掌握。经常引导学生反思解题结果,可以让学生在解决数学问题的过程中不断总结经验教训,自觉调控思维的进程,及时发现错误并给予纠正,培养思维的批判性。
总之,反思是例题教学后的重要环节。有了反思要求,教师就不会一味强调机械、重复的训练解题技巧。因此,在课堂教学后,教师要经常引导学生学会反思,逐步养成反思的意识和习惯,真正成为学习的主人。
参考文献:
[1]庄加荣.分层导学实践研究[J].教育评论,2017,(01).
[2]何井山.初中数学的“分层教学”浅谈[J].新课程导学,2014,(32).
[3]石桂兵.例谈在中学物理教学中对典型例题的深化和改造[J].中学时代,2012,(18).
[4]余建国.好的解题教学应“四有”[J].中小学数学(高中版),2019,(Z1).
[5]紫维国.解题教学中能力的培养[J].内蒙古统计,2005,(02).
[6]王神华.有关解题教学的几个认识[J].福建中学数学,2005,(01).
[7]张本春,陆学政,范银萍.解题教学应注重学生思维的暴露与分析——从“押中题的尴尬”谈起[J].中学数学教学参考,2019,(Z1).
[8]刘生根.解题教学:“寻源”方可“显流”[J].中学数学教学参考,2019,(08).
(责任编辑 付淑霞)

