考虑低碳的场桥全局调度多目标优化

于 蒙，吕艳洋，李文峰

（武汉理工大学 物流工程学院，湖北 武汉 430063）

1 引言

随着中国持续推进经济全球化，国内货物贸易需求迅速提升，密集的海运航线和港口操作产生了大量的碳排放。因此，有必要对我国集装箱码头的运作管理进行低碳研究，降低港口碳排放量，提高港口运营效率。

国内外学者对于绿色港口、低碳港口理论和场桥调度优化问题的研究已有较长的历史。单场桥作业调度的研究主要考虑场桥路径优化问题和场桥操作次序问题。韩晓龙，等[1]分别运用启发式算法和模拟退火算法对单箱区单场桥调度问题进行研究，通过两种方法的结果对比得出模拟退火算法更优的结论。KIM，等[2]以单个场桥为研究对象，研究了外集卡进场作业序列问题。NgWC，等[3]通过分值定界法考虑集装箱任务准备时间不同情况下的场桥调度问题。

多场桥作业调度问题的研究主要针对多场桥同时作业的安全距离以及多场桥在不同箱区分配的问题。He，等[4]以完成任务组总的迟延时间和场桥能源消耗最小化为目标，构建场桥调度混合整数规划模型。贾志刚[5]以延迟任务量、转场总时间与空闲总时间三者最小化为目标构建了场桥的调度模型，将启发式算法和遗传算法相结合来优化求解。Jin，等[6]对堆场空间分配和场桥配置整合优化问题进行了研究，为集装箱分配堆存子箱区，明确各时段场桥的工作区域。郑红星，等[7]对混堆箱区多场桥调度问题展开研究，并且考虑内外集卡等待时间以及内外集卡等待的优先级问题。Liang，等[8]建立了包括堆存子系统、场桥调度子系统和协调控制子系统的协调优化模型，为进口箱分配堆存箱区，并确定了场桥作业计划。Speer，等[9]通过仿真模型详细讨论了场桥移动干涉等约束，并提出用分支定界法求解场桥的实时调度问题。梁承姬，等[10]研究单个箱区中多台场桥在干扰情况下基于混堆模式的存取箱同时进行的调度问题。黄晓波，等[11]考虑根据装卸过程中所产生的移动碳排放、装卸碳排放和准备碳排放3种排放源，建立了轮胎式龙门吊调度的混合整数规划模型，目标是使轮胎式龙门吊的碳排放量达到最小。周颖，等[12]考虑用全自动轨道式龙门起重机替换轮胎式龙门吊，在堆场计划作业量不变的基础上，以降低堆场碳排放量为约束，建立多阶段混合整数规划模型。

综上，现有场桥研究大多考虑场桥行走路径、完工时间以及堆场作业成本，基于碳排放量最小化的场桥作业优化问题研究较少。因此，本文综合考虑场桥全局调度以及场桥与集卡相互作业关系，建立以堆场作业过程中场桥与集卡碳排放量和作业成本最小化以及场桥转场次数最小化为评价指标的多目标约束优化模型。

2 问题描述

场桥全局调度作业会产生不必要的设备准备时间即设备非作业时间，如集卡与场桥的相互等待时间和场桥的移动和转场时间。所以，在减少碳排放量时还需要保证港口作业效率。因此，本文从码头实际情况出发，对于场桥装卸过程中碳排放源进行详细分析，综合考虑5种排放源并考虑多台场桥空间上的不可跨越性和其他约束条件，兼顾场桥的作业效率和作业成本以及碳排放量，建立以场桥与集卡的综合碳排放量最小和综合作业成本最小以及场桥转场次数最少为评价指标的多目标函数的混合整数规划模型，解决场桥移动路径问题和装卸任务指派问题。

场桥移动碳排放C0随着行驶距离增加而增加，场桥装卸碳排放C1随着服务集装箱的数量增加而增加，场桥准备碳排放C2随着停驻次数增加而增加，场桥与集卡的相互等待碳排放C3和C4随着两者相互等待时间的增加而增加。设备单次作业碳排放量见表1。

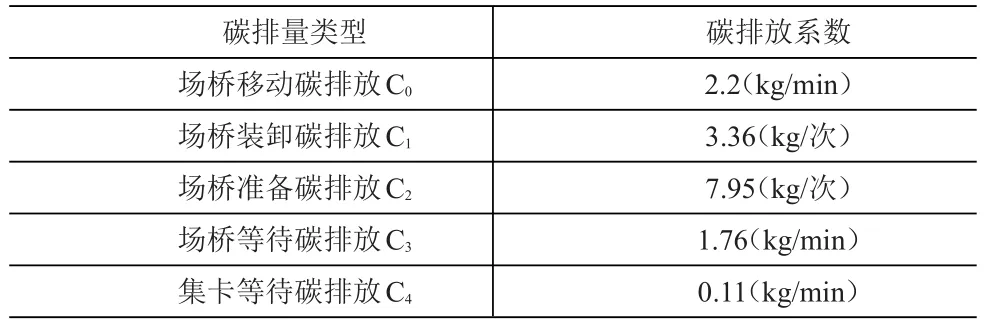
表1 设备单次作业碳排放量

3 模型建立

3.1 模型假设

（1）堆场上场桥操作任务都以20英尺标准集装箱（TEU）为单位，且将同一箱区同一贝位作为一个任务组来处理；

（2）忽略每台场桥的设备老旧可能导致的能耗不同以及场桥司机驾驶经验不同的影响，假设每台场桥的移动成本相同；

（3）在同一箱区内操作的场桥之间必须保持一定的距离和不可跨越以保证安全；

（4）场桥初始时刻位于其初始操作任务所在贝位，操作完最后一个任务后即停留在原地直至所有场桥作业结束；

（5）场桥操作完一个任务随即沿着最短路径移动到下一个任务所在贝位处；

（6）计划期内场桥的任务量、任务所在位置、集卡到达时间以及场桥操作任务的时间都是已知的；

（7）堆场列间过道两侧的贝位数相同，且箱区之间过道宽度为两个贝位，列间过道宽度为三个贝位；

（8）每一个时间段贝位分配的集装箱数量不能超过任一场桥在该时间段的总工作能力（每小时场桥最多可处理20个集装箱任务的装卸）。

3.2 模型相关参数说明

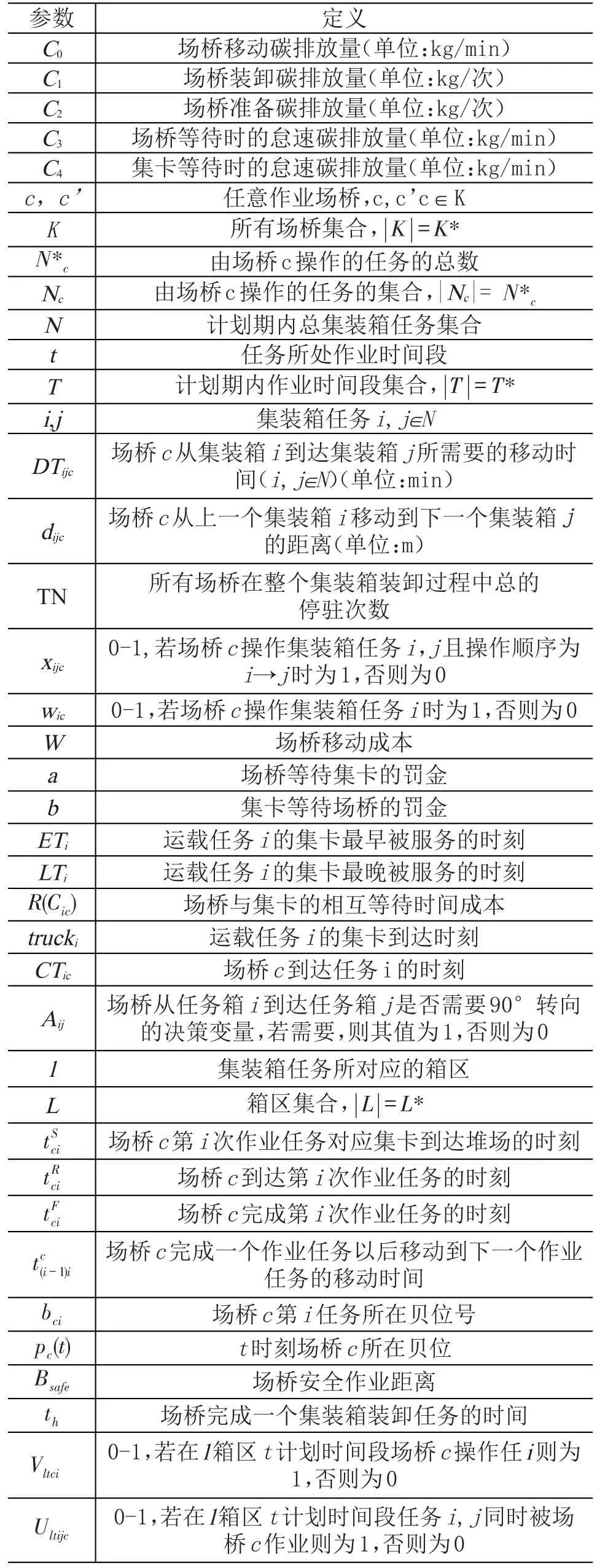
表2 模型中的基本参数

3.3 数学模型

考虑低碳的场桥全局调度多目标优化模型可表述为下面的形式。

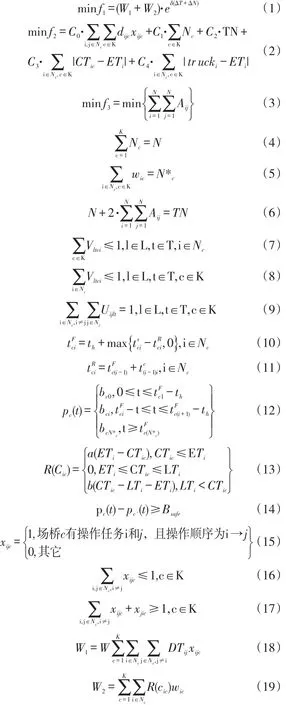
式（1）表示考虑场桥作业时间和作业任务均匀

条件下的场桥作业成本和场桥与集卡的相互等待成本之和最小。引入指数函数eδ(ΔT+ΔN)来考虑场桥作业时间和场桥作业任务量的均衡，其中ΔT表示最大场桥完成作业时间与最小场桥作业完成时间的差值；ΔN表示最大场桥作业任务量与最小场桥作业任务量的差值；式（2）表示场桥与集卡总碳排量最小；式（3）表示所有场桥的转场次数总和最小；式（4）表示所有场桥操作任务总数为N；式（5）表示由场桥c操作的任务数为N*c；式（6）表示场桥停驻次数等于装卸任务总数与2倍场桥转弯次数的和；式（7）保证在任意一个计划时间段内任意一个集装箱任务组只能分配给一台场桥进行作业；式（8）保证任意一个计划时间段内一台场桥只能同时操作一个集装箱任务组；式（9）保证任意一个计划时间段内每个箱区至多有2台场桥同时工作；式（10）-（11）分别表示场桥各任务的完成时刻和场桥到达作业任务的时刻之间的关系；式（12）用于计算场桥各时刻所在贝位；式（13）表示场桥与集卡的相互等待时间成本的计算函数；式（14）保证场桥间留有安全作业距离；式（15）表示场桥c对任务i，j的示性函数；式（16）表示任意一个场桥进行作业时至多有一个紧前作业和紧后作业；式（17）任意一个场桥进行作业时至少有一个紧前作业或紧后作业；式（18）表示场桥c从任务i行驶到任务j的场桥移动成本；式（19）表示场桥与集卡的相互等待时间成本。

4 模型求解

非劣排序遗传算法Non-dominated Sorting Genetic Algorithm-II（NSGA-II）[13]从经典的遗传算法发展而来，具有良好的自组织性和自适应性，及容错能力强等优点，易收敛且具有个体多样性。模拟退火算法Simulated Annealing Algorithm（SA）是一种基于随机寻优方式的目标优化算法，具备较强的局部搜索能力。所以本文采用遗传算法与模拟退火算法相结合的混合非劣排序遗传算法求解模型，并给出数值分析算例证明了本文模型和算法的有效性。

4.1 染色体编码

采用基于工序的实数编码，场桥部分编码规则为：设定4台场桥在堆场同时作业，按照每一个任务组分配的集装箱数量随机分配4台场桥。其中染色体示意图如图1所示，以14个算例数据为例，14个作业任务分别对应一个指定的场桥，并且任务分配满足约束条件（7）-（8）。

图1 染色体示意图

4.2 种群初始化

本文使用Matlab中的遗传算法工具箱对初始种群进行设定。遗传算法工具箱得出的初始种群需要判断是否满足场桥作业安全距离以及同一时间同一箱区最多有两台场桥同时作业的限制，即约束条件（9）和（14）。为达到上述效果，对每一场桥的作业任务设置了算法判断过程，判断步骤如下：

步骤1：对每一个场桥的所有作业任务按照作业时间从小到大排序；

步骤2：选择1、2两个任务判断是否在同时作业，若是则进行步骤3，否则选择2、3两个任务继续步骤2；

步骤3：继续判断下一个任务是否与前两个任务同箱区，若是则判断安全距离，否则选择2、3两个任务继续步骤2；

步骤4：若1、2两个任务处于安全距离则判断2、3是否同时作业，否则结束程序；

步骤5：按照上述步骤依次判断所有任务。

4.3 多目标适应度评价

多目标优化问题中，需要协调折中各个目标函数，得到由折中解构成的一个最优解集。Pareto方法适合解决多目标问题，帕累托层是根据个体之间的支配关系将个体划分为不同的层级，每个解所处的层数越低，解的质量越高，第一层级个体不被任何个体支配，即帕累托前沿解集。除了利用层级来划分个体收敛性的优劣，算法利用多样性指标拥挤距离来确定具有相同层级个体的优劣。其中非支配排序和拥挤度排序的具体实现步骤如下：

4.3.1 非支配排序

步骤1：对每一个个体i∈N，判断个体i支配的其他个体总数individual(i).n和支配个体i的其他个体集合individual(i).p；

步骤2：对每一个目标函数k∈N，判断个体i与j的支配关系；

步骤3：individual(i).n=0的个体即非支配排序等级最高的个体，令其front=1；

步骤4：按照上述步骤1-3依次判断出所有个体的排序等级。

4.3.2 拥挤度排序

步骤1：对每一个非支配排序层次内的个体按照第k个个体的目标函数f_k排序，设排序第一和排序最后一个个体的拥挤度为无穷大。即f_min=f_max=inf，其它个体的拥挤度y为：

步骤2：按照步骤1依次计算每一个目标函数得出的拥挤度排序值；

步骤3：将各个目标函数得出的拥挤度值分别相加得出每一个个体的总排序值。

4.4 混合非劣排序遗传算法过程

本文采用遗传算法与模拟退火算法相结合的混合非劣排序遗传算法，将模拟退火算法引入到NSGA-II中，解决了NSGA-II局部搜索能力较弱的问题，其步骤如下：

步骤1：按照4.2步骤随机初始化种群；

步骤2：评价每一个个体的适应度并进行非支配排序和拥挤度排序，得出Pareto解；

步骤3：确定初始温度；

步骤4：用遗传算法得到新种群，并更新Pareto解；

步骤5：进行退温操作；

步骤6：若满足运算精度或迭代次数等停止条件时，输出当前最优值，搜索结束，否则返回步骤4继续搜索。

4.5 基于Analytic Hierarchy Process（AHP）的多目标决策

基于Pareto求解得到一组Pareto解集即Pareto前沿，而对于实际问题，需要决策者筛选一个最满意的非劣解用于实际生产。AHP是一种将定量和定性有效结合处理多目标问题的决策技术，可以运用于多目标方案的决策。本文采用AHP方法，以多个目标为决策准则，对得到的Pareto前沿给出的非劣解方案进行排序和评估。AHP递阶结构如图2所示。

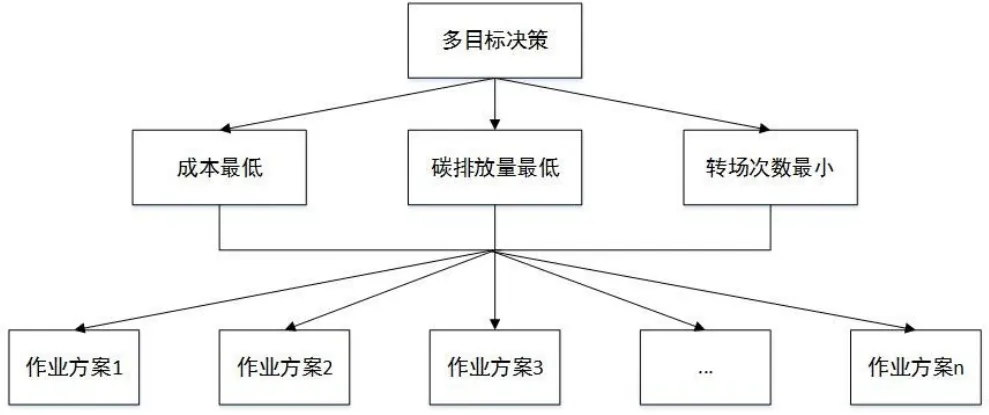
图2 多目标方案的AHP递阶结构

5 算例分析

采用数值实验来验证本文所提出模型和算法的有效性。算法由Matlab2016编程实现，所得结果均在Inter Core i5以及8RBRAM的x64PC上测得。

5.1 数据输入

通过采集某集装箱港口实际运营数据，验证本文所建立模型以及用于求解模型的启发式算法的有效性。选取某港口3个出口箱区进行研究，箱区示意图如图3所示。每一个箱区包含两列，每一列包含30个贝位。本文设定水平方向的中间过道为2个贝位距离，垂直方向的中间过道为1个贝位距离。在计划时间120min内处理40个集装箱任务数量，可用的场桥数量为4台。场桥移动单位时间成本，场桥与集卡的相互等待成本等数据在主程序中给出。

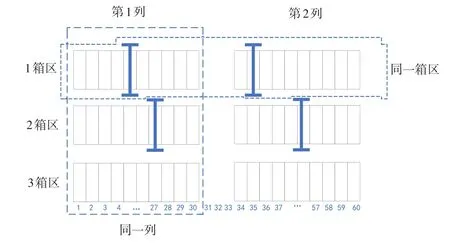
图3 箱区示意图

5.2 结果分析

针对本文模型，采用5.1节试验数据，通过MATLAB运用遗传算法和模拟退火算法相结合的混合算法求解仅考虑成本的单目标方案，用加入模拟退火算法的非劣排序遗传算法（多目标方案需要用非劣排序）求解本文提出的综合考虑作业成本、碳排放量和场桥转场次数的多目标方案。为了保证两种方案对比的有效性，两种方案的遗传算法和模拟退火算法参数设置完全相同，具体参数见表3。

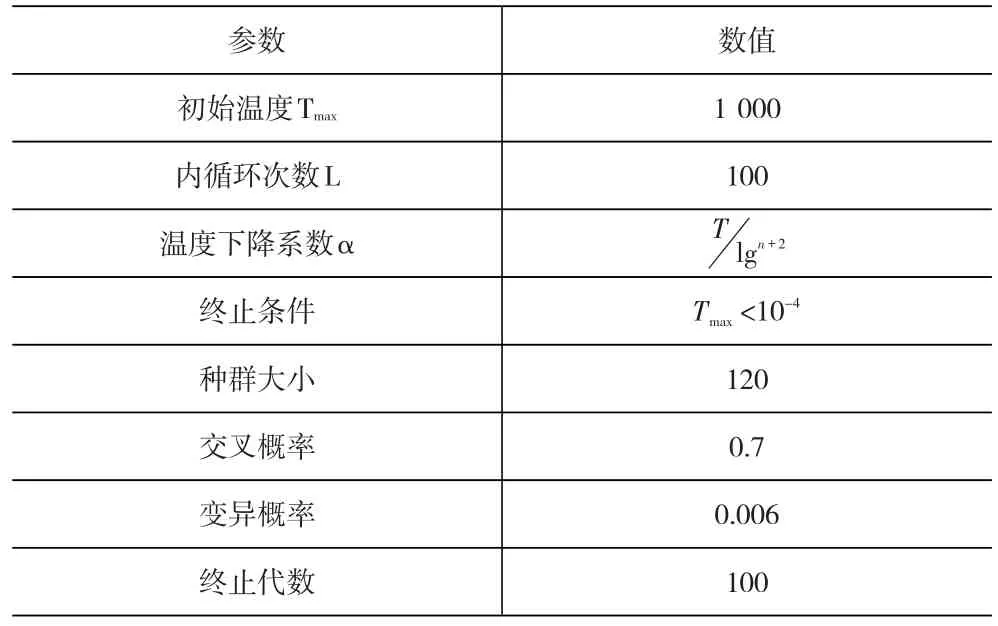
表3 算法参数设置

图4和图5分别为多目标与单目标两种方案所得解的计算结果对比图。

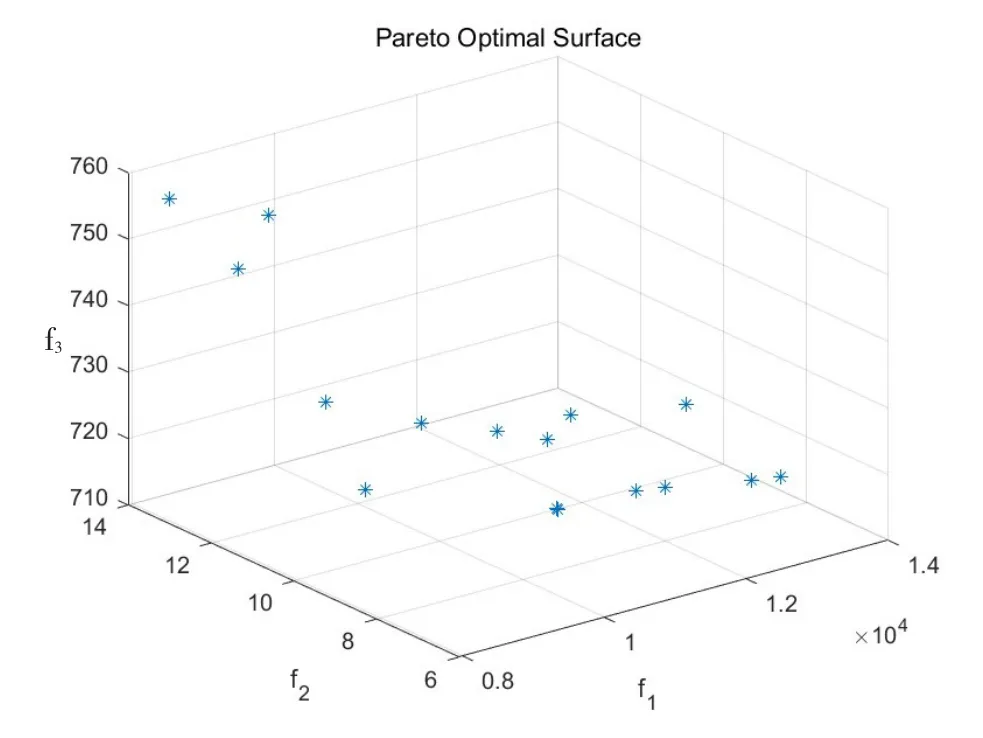
图4 多目标方案求解所得Pareto前沿

由图5可知，单目标方案进化至49代时目标值收敛于7 553元。从图4可知，多目标方案获得的15种结果较为集中，表明该算法收敛。对于该15个非劣解的平衡方案，运用层次分析法可以分析得到一个最优方案，层次分析法决策结果见表4。

图5 单目标方案算法收敛过程

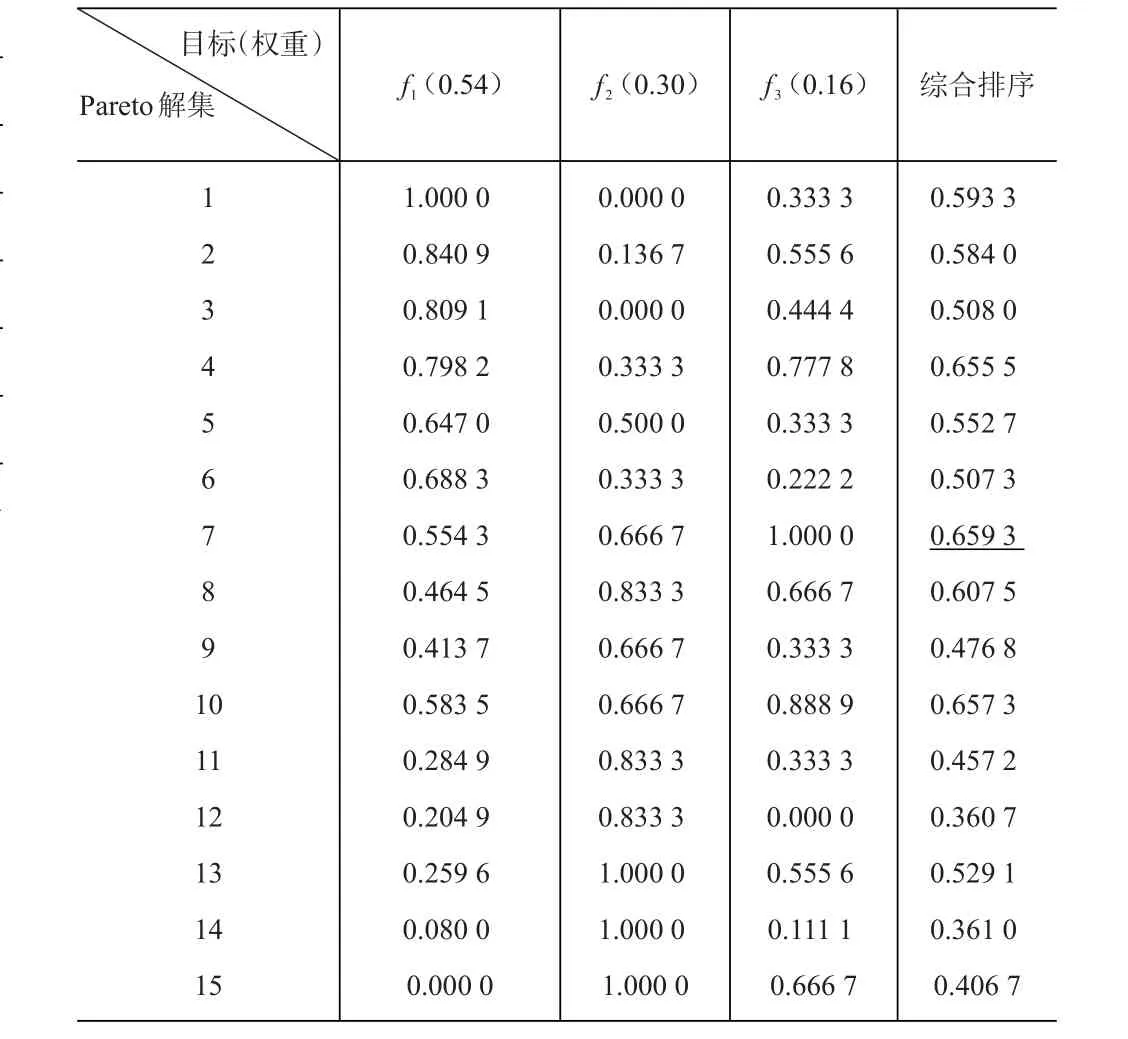
表4 评价决策结果

故Pareto方案7为多目标方案的最合适方案。即多目标方案成本为10 220元，碳排放量为728.8kg，转场次数为9次。

把多目标方案最优结果与单目标方案的最优结果做对比，对比结果见表5。

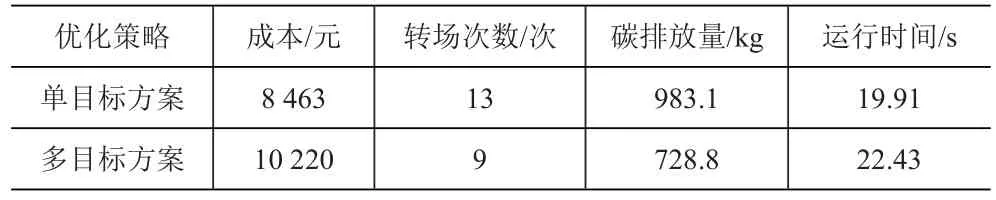
表5 不同方案结果对比

对比两个方案的结果，可以得出多目标方案实验运行时间增加2.52s，相差很少可以忽略。多目标方案转场次数相对于单目标方案减少了4次，总成本增加20.76%，但是其总碳排放量减少34.89%，有效的降低了场桥工作的碳排放量。

6 结语

本文整体考虑场桥与集卡作业过程中的碳排放源，降低港口作业的碳排放，同时保证港口作业效率，减少港口的运营成本。本文创新点在于同时考虑场桥的碳排放量最小化和作业成本最小化以及转场次数最小来确定场桥的作业方案，还考虑了场桥与外集卡的作业联系，提高了堆场的作业效率。使用混合非劣排序遗传算法求解场桥的最优作业方案。数值算例显示碳排放量降低34.89%，证明了模型和算法的有效性。但本文没有考虑翻箱因素和集卡到达时间不确定性的影响。并且模型假设每个任务作业时间已知，但是在实际操作中进出口箱的选位和作业先后顺序都会对堆场作业造成影响，后续的研究方向是将场桥的多箱区调度与集卡到达时间和堆存位置选择的不确定性进行集成优化。